Strain localization of Mohr-Coulomb soils with non-associated plasticity based on micropolar continuum theory

Jianbin Tang,Xi Chen,Liusheng Cui,Zongqi Liu

State Key Laboratory of Urban Underground Engineering of Ministry of Education,Beijing Jiaotong University,Beijing,100044,China

Keywords: Strain localization Micropolar continuum Mohr-Coulomb (MC) model Non-associated plasticity Second-order cone programming

ABSTRACT To address the problems of strain localization,the exact Mohr-Coulomb (MC) model is used based on second-order cone programming (mpcFEM-SOCP) in the framework of micropolar continuum finite element method.Using the uniaxial compression test,we focused on the earth pressure problem of rigid wall segment involving non-associated plasticity.The numerical results reveal that when mpcFEM-SOCP is applied,the problems of mesh dependency can be effectively addressed.For geotechnical strain localization analysis involving non-associated MC plasticity,mpcFEM-SOCP in conjunction with the pseudo-time discrete scheme can improve the numerical stability and avoid the unreasonable softening issue in the pressure-displacement curves,which may be encountered in the conventional FEM.It also shows that the pressure-displacement responses calculated by mpcFEM-SOCP with the pseudo-time discrete scheme are higher than those calculated by mpcFEM-SOCP with the Davis scheme.The inclination angle of shear band predicted by mpcFEM-SOCP with the pseudo-time discrete scheme agrees well with the theoretical solution of non-associated MC plasticity.

1.Introduction

The strain localization is generally considered as a primary precursor for the progressive failure of a geotechnical system (e.g.Borja and Lai,2002;Arslan and Sture,2008).It has been noted,however,that the conventional finite element method (FEM) suffers from the pathological mesh dependency,and may fail to accurately capture the strain localization (e.g.Borja and Lai,2002;Chen et al.,2014).Hence,to reveal the progressive failure of a geotechnical system,a numerical method capable of accurately simulating geotechnical strain localization is needed.

Over the past decades,the micropolar (or Cosserat) continuum theory,which introduces the internal characteristic length into the classical continuum,has been proposed and applied to the strain localization analysis successfully based on FEM(e.g.Mühlhaus and Vardoulakis,1987;Arslan and Sture,2008).Based on the micropolar continuum theory,the Drucker-Prager(DP)criterion has been widely used (e.g.Li and Tang,2005;Sabet and Borst,2019;Tang et al.,2022).However,incorporating the Mohr-Coulomb (MC)model into the micropolar continuum mechanics is still a challenging issue.

Different from the classical continuum,the stress tensor usually loses symmetry due to the presence of couple stress in the micropolar continuum.The generated Mohr’s circle of non-symmetric stress state is geometrically difficult to represent the yield criterion(Chang et al.,2017).By generalizing the strength criterion from the symmetric Mohr’s stress state to non-symmetric stress state,Iordache and Willam (1998) revealed that the micropolar effect relies on the internal characteristic length and degree of nonsymmetry in stress and strain.Figueiredo et al.(2004) suggested that the characteristics of generalized micropolar continuum can be reflected into the Mohr’s circles and strength envelopes,and they also showed the graphical Mohr’s circle representation of stresses for such analysis.As shear stress can be decomposed into the‘symmetric’ and the ‘anti-symmetric’ parts,sliding-and rollingfriction yield models are proposed.Papanicolopulos and Veveakis(2011) proposed a multiple-yield-surface generalization of the model using energy dissipation,while the conventional constitutive models are enhanced through the stress invariants to incorporate the micropolar effects(Alsaleh et al.,2006).Alternatively,de Borst (1993) proposed the J2-flow theory for micropolar continuum.The non-symmetric stress component and the couple stress component are introduced into the DP model.Some researchers tried to develop the MC model and give extension of the Lode’s angle for the micropolar continuum.Nevertheless,these computations are still based on the conventional FEM framework (e.g.Manzari,2004;Panteghini and Lagioia,2022).In the conventional FEM,the ‘rounding-off’ scheme has been commonly used to smooth the sharp edges and apex of the MC strength envelope to remove the gradient singularities at these locations (e.g.Griffiths and Willson,1986;Abbo et al.,2011).However,within the framework of FEM based on mathematical programming,such as FEM in second-order cone programming (FEM-SOCP) (e.g.Ukritchon and Keawsawasvong,2018;Mohapatra and Kumar,2019;Sun and Yang,2021;Nguyen and Vo-Minh,2022),the ‘rounding-off’ treatment of the MC yield surface can be obviated.

On the other hand,Pamin et al.(2003)observed that,when the conventional FEM is used to analyze those problems involving nonassociated plasticity,unstable stress and poor convergence may occur due to the ill-posedness of the boundary value problem(BVP).This matches the observation by Vermeer and de Borst(1984) that non-associated plasticity models may produce nonunique limit loads and lead to unstable structural behavior even for the elastic-perfectly plastic model.Besides,Collins (2002) also noticed that symmetric stiffness matrices are of fundamental importance to numerical stability of elastoplastic analysis,because non-symmetric matrices may occasionally lead to numerical instability.Tschuchnigg et al.(2015) attempted to investigate approaches to overcome possible numerical instability caused by non-associated plasticity,including the one converting the nonassociated soil plasticity into the equivalent associated soil plasticity with the aid of the Davis formula.Some efforts have been made to develop robust methods capable of analyzing geotechnical problems involving non-associated plasticity.Particularly,those methods can indirectly solve geotechnical problems involving nonassociated plasticity but could avoid numerical instability caused by non-symmetric finite element stiffness matrices.For instance,based on the Davis formula or the modified version,a soil of nonassociated plasticity may be converted into a soil of equivalently associated plasticity,so that the factor of safety (FS) of a geotechnical system involving non-associated plasticity can be estimated(e.g.Davis,1968;Oberhollenzer et al.,2018;Chen et al.,2020).Alternatively,if a pseudo-time discrete scheme is utilized,solving a geotechnical problem involving non-associated MC plasticity can be converted to solving a sequence of associated plasticity problems (e.g.Krabbenhoft et al.,2012;Zhang et al.,2016).

By combining the second-order cone programming with micropolar continuum method,Wang et al.(2019) proposed the framework of second-order cone programming optimized micropolar continuum finite element (mpcFEM-SOCP) to overcome the mesh dependence problem.Later,mpcFEM-SOCP was used to analyze the slope stability with emphasis on the strain softening(Chen et al.,2021)and to assess the geotechnical strain localization behaviors in consideration of evolution of internal characteristic length (Tang et al.,2022),respectively.However,the above researches in the framework of mpcFEM-SOCP are all performed based on the DP model.To better analyze the geotechnical strain localization involving non-associated plasticity,the MC model is developed within the framework of mpcFEM-SOCP.

2.Second-order cone programming optimized micropolar continuum FEM for non-associated MC plasticity

2.1.Theory of micropolar continuum

Cone programming can be considered as an extended form of linear programming.Generally,the standard second-order cone programming (SOCP) solution for a problem may be expressed as

where c is the coefficient vector;x is the solution vector;Ax=b is the constraint of linear equation;and K is either the quadratic cone(KQ) or the rotated quadratic cone (KR),as given by

where Rmis the set of real numbers with dimensionm,andxjis thej-th component of x.

In the plane-strain analysis of micropolar continuum,apart from the two translational displacement components (i.e.u1andu2),a rotation DOF (ω3) is included for each node,that is

Correspondingly,by introducing the micro-curvatures (χ13andχ23)and the couple stresses(m13andm23),the strain(ε)and stress(σ) vectors are defined respectively as

where ε11,ε22and ε33are the normal strain components;and ε12and ε21are the tangential strain components.Correspondingly,σ11,σ22andσ33are the normal stress components;andσ12andσ21are the tangential stress components.

For each integration point,the equilibrium equation,the compatibility equation,and the constitutive equation shall be provided.Generally,the static equilibrium equation is given as

where f is the vector of body force,and ∇is the differential operator shown as follows:

The compatibility equation can be expressed as

In elastoplastic theory,the total strain increment(Δε)is composed of the elastic strain increment(Δεe)and the plastic strain increment(Δεp):

For elastic micropolar continuum,the constitutive relation is given as

where Δσ is the stress increment,and Decan be given by

whereGmis the micropolar shear modulus,andGm=0.5Gis taken here in terms of numerical experiences (e.g.de Borst,1993;Tang et al.,2022).

As a macroscopic physical parameter characterizing the microscopic characteristics of soil particles,the internal characteristic lengthlcis utilized to model the shear band thickness.In practical applications,lcshall be calibrated based on laboratory tests (e.g.Alshibli and Sture,2000;Rattez et al.,2020).Nevertheless,considering the complexity and difficulty of defininglc(Voyiadjis et al.,2005),constantlcis assumed in the following numerical experiments.Additionally,it is emphasized that mpcFEM-SOCP withGm≈0 andlc≈0 reduces to the classical continuum-based FEM-SOCP.LandGare the Lamé constants,which may be further expressed by the elastic modulusEand the Poisson’s ratiov,that is

2.2.Second-order cone form of MC criterion for micropolar continuum

The MC criterion in micropolar continuum is reformulated in the deviatoric plane as shown in Fig.1,and the corresponding MC yield criterion with the positive compression is expressed as

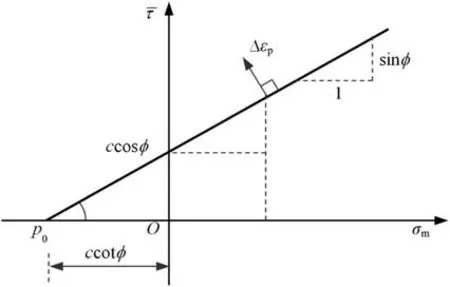
Fig.1.MC criterion for micropolar continuum in the deviatoric plane.

wherecandϕare the cohesion and the internal friction angle,respectively;andσmanddenote the mean normal stress and the generalized shear strength in micropolar continuum,respectively,which can be given as

Evidently,ifm13=m23=0 andσ12=σ21,the generalized shear strengthdegenerates to the shear strength τ of classical continuum.By substituting Eqs.(14)and(16)into the yield criterion in Eq.(13),the micropolar continuum-based MC criterion is derived as

By referring to Eqs.(2a)and(2b),the following set of variablesqjwithj=[1,5] are defined as

As a result,Eq.(17) may be rewritten into the following quadratic cone:

whereipis the index of integration point.

After the constraint of Eq.(19) is incorporated into Eq.(1),the SOCP form of the micropolar continuum considering the MC criterion can be solved.

To model the strain softening of granular soil,a piecewise linear function with respect to the equivalent plastic strain is hypothesized for the cohesionc(e.g.Li and Tang,2005;Zhu et al.,2021) as

wherec0is the initial cohesion,hpis the (negative) softening modulus of cohesion,and εeqis the equivalent plastic strain at each integration point.The strain-softening model was simplified as the elastic-perfectly plastic model whenhp=0.The equivalent plastic strain at each integration point is the work conjugacy invariant given as (Perić et al.,1994)

where εpis the plastic strain,and Qεcan be give as

2.3.A pseudo-time discrete scheme for non-associated MC plasticity

For non-associated MC plasticity in micropolar continuum,the plastic potential function may be defined as

whereψis the dilatancy angle satisfyingψ≤ϕ.

Since the SOCP solver is only applicable to the optimization problem with associated soil plasticity,a pseudo-time discrete scheme with adaptive error control was implemented for those geotechnical problems with non-associated plasticity,and the intermediate associated plasticity problems can be solved (e.g.Krabbenhoft et al.,2012;Zhang et al.,2016).In the pseudo-time discrete scheme,a time step factorλ∈(0,1) is introduced to update the internal friction angle towards the dilatancy angle.The internal friction angle () is updated as

whereδ=ϕ-ψis the difference ofϕandψ,reflecting the degree of non-associativity;tis the pseudo-time step;andλis the time step factor.By referring to the geometric relation in Fig.2,the equivalent cohesion of each integration point can be derived from the following relation at thet-th pseudo-time step:

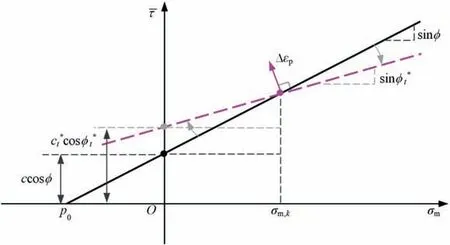
Fig.2.Adaptive pseudo-time discrete scheme for non-associated MC plasticity in the deviatoric plane.

whereσm,kdenotes the mean normal stress at thek-th incremental step,and the equivalent cohesionct*can be updated in terms of the internal friction angleϕt*.The convergence of the adaptive pseudotime discrete scheme is attained,until the following displacementbased convergence criterion,||ut-ut-1||/||ut||≤εu(εuis the convergence tolerance),is satisfied.Once the convergence criterion is met,ϕt*=ψis set andct* is calculated by Eq.(25) for the equivalent associated soil plasticity.The detail on the adaptive pseudo-time discrete scheme is shown in Fig.3.

Fig.3.Adaptive pseudo-time discrete scheme for non-associated plasticity problem.

2.4.Hellinger-Reissner variational principle and finite element discretization

To derive the finite element formulas,the stress and displacement variables are interpolated with the shape (or interpolation)function for stress and displacement (i.e.Nσand Nu),respectively,as

According to the Hellinger-Reissner (HR) variational principle(Reissner,1950),the functional∏HR(u,σ)of the entire system may be expressed in terms of two independent fields,i.e.the displacement u and the stress σ.The stationary value of the functionalδ∏HR(u,σ)=0 results in a saddle point of the functional,which corresponds to a min-max optimization problem with the following incremental form (Wang et al.,2019)

whereΩand ∂Ωrepresent the solution domain and its boundary,respectively;t is the vector of traction force;and Ceis the elastic compliance matrix.The increments are Δuk+1=uk+1-uk,Δσk+1=σk+1-σk,and the new state variables uk+1and σk+1are updated from the known state variables ukand σk.When the MC criterion is adopted,the constraint condition of yield functionf(σ)≤0 expressed by Eq.(19) shall be incorporated into Eq.(27).

Based on the elastoplastic micropolar continuum model and the above finite element approximations,the converted SOCP problem with both the loads and the displacement constraints is given as

where uk+1is the vector of the prescribed nodal displacements;k+1is the vector of unknown nodal reaction force;Niptis the total number of integration points in the entire solution domain;I is the index diagonal matrix with its diagonal entry value to be either 0 representing the free displacement DOF or 1 representing the prescribed displacement;for theip-th integration point,ip，k+1is the stress vector at the (k+1)-th incremental step;Tipand tipare the coefficient matrix and vector related to the yield function;is the set of real numbers,refer to Eq.(19);ξipis the auxiliary variable of objective function in optimization problem;and Lip,ηip,andsipare auxiliary variables of constraint functions in optimization problem.It is noteworthy that when cancelling the terms related tok+1,Eq.(28) is simplified as the one solely with load boundary conditions.

3.Numerical experiments

The mpcFEM-SOCP with the incorporated MC failure criterion is employed to study the strain localization of the geotechnical problems involving non-associated MC soil plasticity.The corresponding finite element program is coded in Fortran and the analysis results are visualized by the self-developed Python graphic user interface.

3.1.Strain localization of soil column in uniaxial compression test

One soil column specimen in uniaxial compression is modeled,as shown in Fig.4.In this model,the nodes on the bottom boundary were fully fixed.The soil material in the test is homogeneous with the Young’s modulusE=10 MPa,Poisson’s ratiov=0.3,cohesionc=10 kPa,angle of internal frictionϕ=40°and dilatancy angleψranging from 0°to 40°.To better observe the scenario of nonassociated soil plasticity,the softening of cohesion is not considered in the present soil column,i.e.hp=0.For the micropolar continuum,the micropolar shear modulusGm=0.5Gand internal characteristic length oflc=1 cm are adopted.To investigate the performance of mpcFEM-SOCP,three densities of meshes,i.e.20 × 10 mesh (coarse mesh with the total number of finite elements,nels=200),40 × 20 mesh (intermediate mesh withnels=800) and 80 × 40 mesh (fine mesh withnels=3200) corresponding to the average mesh size ofle=10 cm,5 cm and 2.5 cm,respectively,are generated.For the specimen under uniaxial compression,the total vertical displacementuy=2 cm of rough rigid footing is applied in 20 equal increments(i.e.Nstep=20,the vertical displacement increment Δuy=0.1 cm).

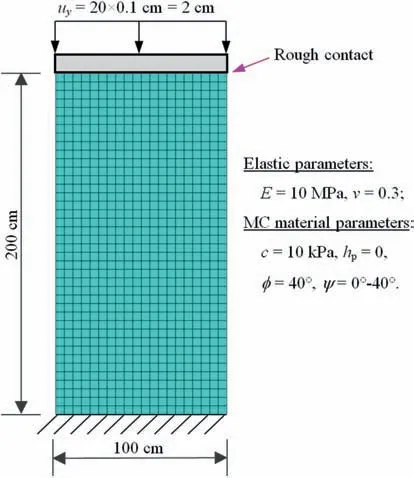
Fig.4.Geometry and finite element mesh(nels=800)for one soil column specimen in uniaxial compression subjected to prescribed vertical displacement.

As illustrated in Fig.5,the pressure-displacement curves obtained by conventional FEM and mpcFEM-SOCP involving nonassociated soil plasticity are plotted.The uniform bottom pressure of rough rigid footing is calculated by averaging the nodal reaction forces at ‘loaded’ area.The non-symmetric FEM linear solver built in conventional FEM is generally utilized.Nevertheless,when mpcFEM-SOCP is applied,the pseudo-time discrete scheme shall be implemented,and the resulting method is denoted as mpcFEMSOCP(NA-Time).When the conventional FEM is applied,three sets of pressure-displacement curves attained from three mesh densities appear to be evidently different as shown in Fig.5a.The non-physical strain softening at the post-failure stage could be observed,particularly for the curves attained from the finer meshes(e.g.nels=800 andnels=3200).As a result,it is difficult to attain a complete pressure-displacement curve due to unstable numerical calculation.The unstable numerical calculation is interpreted from the equivalent plastic strain contours shown in Fig.6a.It shows that the pattern and thickness of shear bands appear to be indeterminate with the mesh being gradually refined.However,it is found from Fig.5a that three curves attained by mpcFEM-SOCP(NA-Time)are basically consistent.For example,when the prescribed displacement ofuy=2 cm is applied,the relative error of the pressure calculated by mpcFEM-SOCP(NA-Time) withnels=200,compared to that calculated by mpcFEM-SOCP(NA-Time) withnels=3200,is only 0.61%,indicating that the pathological mesh sensitivities are effectively alleviated or even eliminated by mpcFEM-SOCP(NA-Time).Additionally,the non-physical softening behaviors associated with conventional FEM can be overcome by mpcFEM-SOCP(NA-Time).Fig.6b shows the strain localization pattern of the soil column specimen calculated by mpcFEMSOCP(NA-Time),which evidently is stable and consistent for different mesh densities.

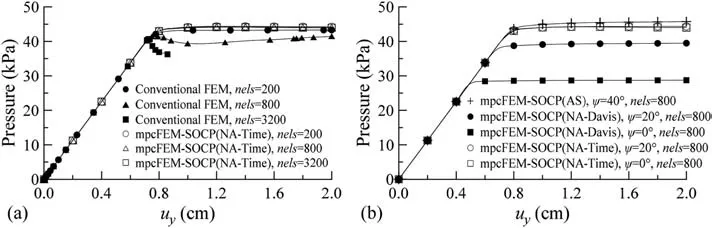
Fig.5.Pressure-displacement curves obtained by conventional FEM and mpcFEM-SOCP for: (a) Different mesh densities with ψ=0°,and (b) Different values of ψ (nels=800).

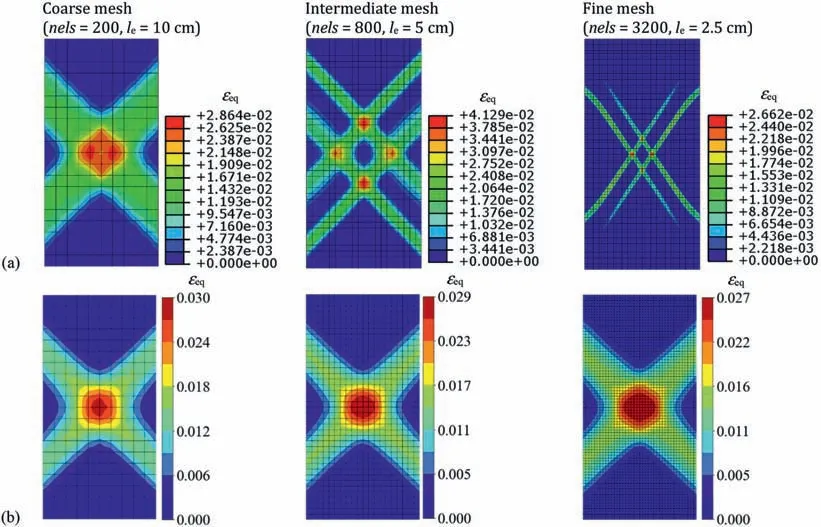
Fig.6.Equivalent plastic strain contours obtained by conventional FEM and mpcFEM-SOCP subjected to uy=2 cm (or Aborted) involving ψ=0°: (a) Conventional FEM and (b)mpcFEM-SOCP(NA-Time).

Alternatively,we apply the Davis formula (Davis,1968) or its modified versions(e.g.Oberhollenzer et al.,2018;Chen et al.,2020)to convert the non-associated plasticity into equivalently associated plasticity.By following the Davis scheme,the strength parameters (c* andϕ*) of equivalently associated plasticity material are defined as

Furthermore,it is noted from Fig.5b that the pressuredisplacement responses corresponding to the Davis scheme and the pseudo-time discrete scheme are compared for different values ofψ.For brevity,mpcFEM-SOCP in conjunction with the Davis scheme,named as mpcFEM-SOCP(NA-Davis),is adopted;while mpcFEM-SOCP involving associated plasticity (i.e.ϕ=ψ=40°) is denoted as mpcFEM-SOCP(AS).From Fig.5b,it can be seen that when mpcFEM-SOCP(NA-Davis) is applied,the calculated limit loads decrease markedly with the decrease ofψ;meanwhile,when mpcFEM-SOCP(NA-Time)is applied,the calculated limit loads may not be affected evidently byψ.For instance,compared to the limit load calculated by mpcFEM-SOCP(NA-Time,ψ=20°) the relative error of limit load calculated by mpcFEM-SOCP(NA-Time,ψ=0°)is only 0.78%;when compared to the limit load calculated by mpcFEM-SOCP(NA-Davis,ψ=20°),the relative error of limit load calculated by mpcFEM-SOCP(NA-Davis,ψ=0°) is 37.26%.Correspondingly,the equivalent plastic strain contours obtained by mpcFEM-SOCP(NA-Davis) and mpcFEM-SOCP(NA-Time) are depicted in Fig.7a and b,respectively,for different degrees of nonassociativity.When mpcFEM-SOCP(NA-Davis) is applied,the inclination angle of shear bands (θIA) almost does not change with the variation ofψ,as illustrated by Fig.7a,revealing that mpcFEMSOCP(NA-Davis) hardly reflects the evolution of strain localization withψ.On the contrary,mpcFEM-SOCP(NA-Time)may capture the evolution of strain localization withψwell.Specifically,theθIApredicted by mpcFEM-SOCP(NA-Time) conforms to the theoretical formula ofθIA=45°+ψ/2.It is noteworthy that the maximum value ofθIAshall be limited by the aspect ratio of the uniaxial compression model,200/100=2 (i.e.arctan(2)=63.43°).

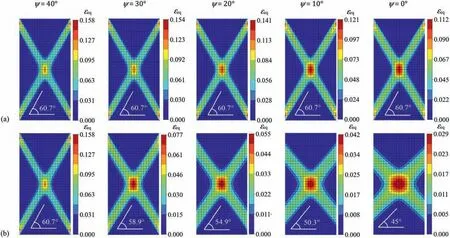
Fig.7.Equivalent plastic strain contours obtained by mpcFEM-SOCP subjected to uy=2 cm when ψ ranges from 40° to 0° (nels=800): (a) mpcFEM-SOCP(NA-Davis) and (b)mpcFEM-SOCP(NA-Time).

To further assess the effectiveness and robustness of mpcFEMSOCP(NA-Time),the stress states at all integration points in the FE model subjected touy=2 cm(nels=800)are plotted in Fig.8.In Fig.8,frepresents the MC yield function and each dot signifies the stress state of one integration point.Nipt=9 × 800=7200 is the total number of integration points in the whole solution domain.To demonstrate the stress states,the number of yielding integration points crossing the strength envelope is recorded asNipYand the maximum positive yield function value is denoted asfmax.In Fig.8a and b,it can be observed that the stress states of most integration points obtained by mpcFEM-SOCP(NA-Time) are lower than the strength envelope,and the distribution of these stress states is more clustered than that obtained by conventional FEM.AIt is interesting that althoughfmax(=0.354) of mpcFEM-SOCP(NATime) is larger than that (fmax=0.0075) of conventional FEM,NipY(=2440) of mpcFEM-SOCP(NA-Time) is smaller than that(NipY=3660) of conventional FEM,which is largely attributed to the different shapes of shear bands.Furthermore,three integration points are selected from three elements at different positions,as shown in Fig.8.It is clear that the yield states of the point ‘3’ is basically consistent for the conventional FEM and mpcFEMSOCP(NA-Time).Nevertheless,the yield states of the point ‘1’ and‘2’are quite different for the two schemes,largely being attributed to unstable shear mode predicted by conventional FEM.

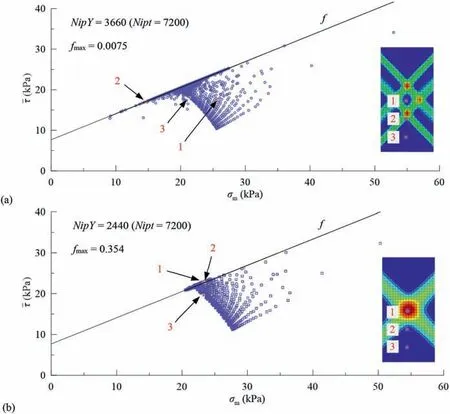
Fig.8.Stress states of all integration points subjected to uy=2 cm (nels=800): (a) conventional FEM and (b) mpcFEM-SOCP(NA-Time).

3.2.Analysis of passive earth pressure of a rigid wall segment

In the second example,the passive earth pressure of a rigid wall segment is studied.Finite element meshes withnels=800 or 5000 elements,which correspond to the average mesh sizele=0.1 m or 0.04 m,are generated.Fig.9 shows the geometry and finite element mesh(nels=800)of a rigid wall segment with a height ofH=1 m.The earth pressure of a rigid wall segment has been analyzed for testing numerical algorithms (e.g.Smith et al.,2013),although it may not be pragmatic.The material parameters for the soil are given as follows: Young’s modulusE=100 MPa,Poisson’s ratiov=0.3,cohesionc=20 kPa,softening modulus of cohesionhp=-20 kPa,angle of internal frictionϕ=30°and dilatancy angleψ=5°;for the micropolar continuum,the micropolar shear modulus isGm=0.5Gand internal characteristic lengthlcis 0.1 m.Before applying the displacement constraint,the soil weight ofγw=18 kN/m3is applied to producing the initial geo-stresses and the resulting displacement is reset to zero.Next,the total horizontal displacement ofux=0.01 m is applied in 20 equal increments (i.e.Nstep=20,the horizontal displacement increment Δux=0.0005 m).For better illustration,only the left half of the domain is visualized.

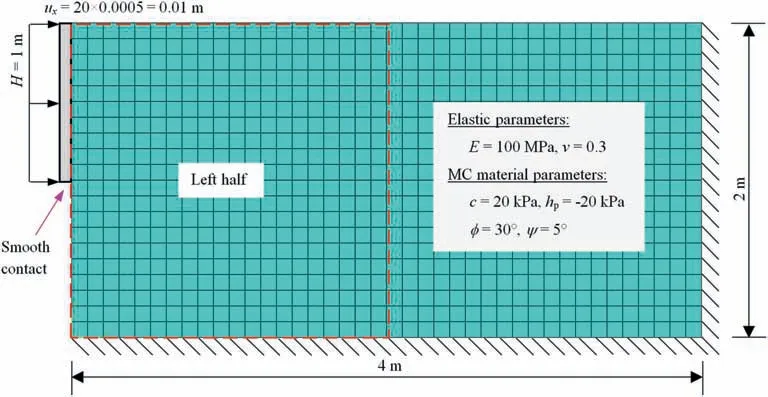
Fig.9.Geometry and finite element mesh (nels=800) for a problem of rigid wall segment.

Fig.10a illustrates the resultant force-displacement curves calculated by FEM-SOCP and mpcFEM-SOCP.The resultant force of the rigid wall segment is calculated from the sum of horizontal nodal reaction forces at ‘loaded’ area.When FEM-SOCP with two mesh densities is applied,the evident deviation of the resultant force-displacement responses at the post-failure stage can be observed (see Fig.10a).For example,under the displacement constraint ofux=0.01 m,the resultant force(79.3 kN/m)calculated by FEM-SOCP with the fine mesh (nels=5000) is about 15.6%smaller than that (91.7 kN/m) calculated by FEM-SOCP with the coarse mesh (nels=800);while the resultant force (107.5 kN/m)calculated by mpcFEM-SOCP with the fine mesh (nels=5000) is only 3.8% smaller than that (111.5 kN/m) calculated by mpcFEMSOCP with the coarse mesh (nels=800),disclosing that mpcFEMSOCP can effectively alleviate the mesh sensitivity of the rigid wall system.Additionally,since the couple stresses are taken into account,the maximum resultant force calculated by mpcFEM-SOCP is generally larger than that attained by FEM-SOCP.

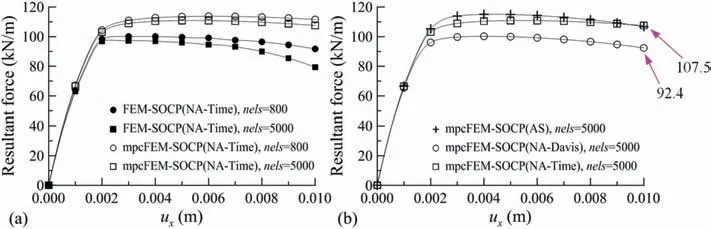
Fig.10.Resultant force-displacement curves obtained by FEM-SOCP and mpcFEM-SOCP: (a) with two mesh densities,and (b) for different non-associated plasticity schemes(nels=5000).

It is observed from the resultant force-displacement curves(see Fig.10b) that the soil with equivalently associated plasticity converted by the Davis scheme tends to yield earlier,so that the resultant force calculated by mpcFEM-SOCP(NA-Davis) is 92.4 kN/m,which is about 14% lower than that (107.5 kN/m) calculated by mpcFEM-SOCP(NA-Time) under the displacement constraint ofux=0.01 m.Hence,direct application of the Davis scheme may evidently underestimate the resultant force.Additionally,under the same displacement constraint,the value of equivalent plastic strain of granular soil involving non-associated plasticity is smaller than that of granular soil involving associated plasticity,so the softening behavior of granular soil at the post-failure stage predicted by mpcFEM-SOCP(NA-Time) is less significant than that predicted by mpcFEM-SOCP(AS).

Fig.11 illustrates the equivalent plastic strain contours of the rigid wall system subjected toux=0.01 m attained by mpcFEMSOCP.According to the Rankine’s theory,the inclination angle of shear band can be calculated theoretically byθIA=45°-ψ/2.Hence,the calculatedθIAis 30°for the soil of associated plasticity,while it shall be 42.5°for the soil of non-associated plasticity.As anticipated,when mpcFEM-SOCP is applied,the thickness of shear band is almost independent of mesh density.By comparing Fig.11d with Fig.11f,it is observed that the failure mechanism or the shear band of the rigid wall system between the associated soil plasticity case and the non-associated soil plasticity case is quite different.Nevertheless,theθIApredicted by mpcFEM-SOCP(NA-Davis) falls between that of mpcFEM-SOCP(AS)and that of mpcFEM-SOCP(NATime),as revealed by Fig.11b or e.Obviously,compared with the Davis scheme,the pseudo-time discrete scheme can produceθIAcloser to the theoretical solution.

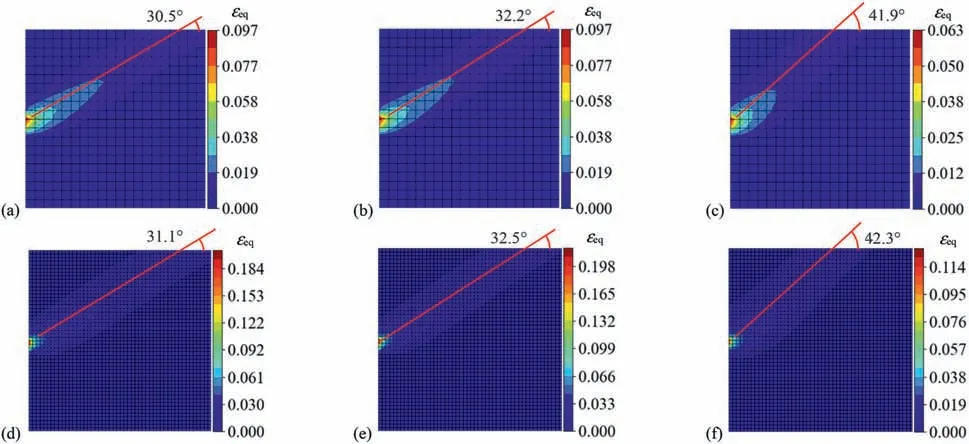
Fig.11.Equivalent plastic strain contours of the rigid wall system subjected to ux=0.01 m obtained by:(a)mpcFEM-SOCP(AS),nels=800;(b)mpcFEM-SOCP(NA-Davis),nels=800;(c) mpcFEM-SOCP(NA-Time),nels=800;(d) mpcFEM-SOCP(AS),nels=5000;(e) mpcFEM-SOCP(NA-Davis),nels=5000;and (f) mpcFEM-SOCP(NA-Time),nels=5000.

Corresponding to Fig.11d-f,Fig.12a-c depicts the microrotation field of the rigid wall system (nels=5000) predicted by mpcFEM-SOCP.It is noted that the localized deformation of granular soil is generally accompanied by considerable rotation and rearrangement of granular soil,so the shear band may also be identified in terms of the micro-rotation.Compared to the case of associated soil plasticity (with the maximum shear dilatancy angle),the maximum micro-rotation in granular soil in the case of non-associated soil plasticity tends to be smaller,implying that the micro-rotation of granular soil could be closely related to dilatancy angle(see Fig.12a and c).In other words,the smaller the dilatancy angle of granular soil with non-associated plasticity,the smaller the rolling-frictional resistance of granular soil.Thus,the rotation effect of granular soil in the shear band is comparatively indistinct.Furthermore,it is observed from Fig.12a and b that the microrotation predicted by mpcFEM-SOCP(NA-Davis) is not much different from that predicted by mpcFEM-SOCP(AS).

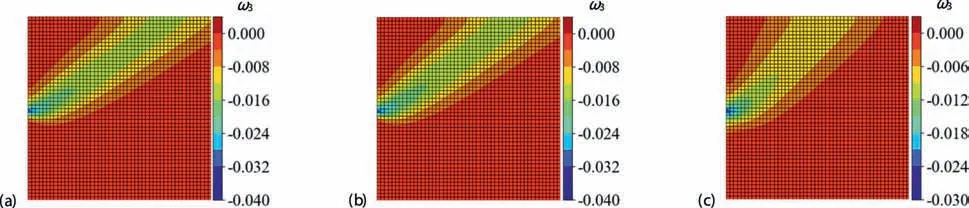
Fig.12.Micro-rotation contours of the rigid wall system(nels=5000)subjected to ux=0.01 m predicted by(a)mpcFEM-SOCP(AS);(b)mpcFEM-SOCP(NA-Davis);and(c)mpcFEMSOCP(NA-Time).

4.Conclusions

To understand the strain localization of geotechnical problems involving non-associated plasticity,two geotechnical examples are investigated.Based on the analysis results,the following conclusions can be drawn:

(1) Although the MC model has been widely accepted in geotechnical applications,it has been rarely implemented in micropolar mechanics compared to the DP model.The difficulty of establishing the plane MC model in micropolar mechanics is partially attributed to non-symmetric stress state.Hence,to better capture the strain localization of granular soil,the MC model is recast to suit for the framework of mpcFEM-SOCP,and the analysis results show that the proposed method can effectively overcome the mesh dependence associated with conventional FEM.

(2) For geotechnical applications involving non-associated plasticity,a pseudo-time discrete scheme is introduced so that the strength parameters of MC model can be updated based on the stress states at the previous incremental step.Using the pseudo-time discrete scheme,the optimization problem involving non-associated soil plasticity can be converted into a sequence of optimization problems with associated soil plasticity.Based on the uniaxial compression test,it is validated that mpcFEM-SOCP in conjunction with the pseudo-time discrete scheme can effectively resolve the unstable numerical solution and improve the numerical stability encountered in the conventional FEM.

(3) It is found that the limit load of a geotechnical system predicted by mpcFEM-SOCP with the Davis scheme is generally lower than that predicted by mpcFEM-SOCP with the pseudo-time discrete scheme.Additionally,the inclination angle of shear band predicted by mpcFEM-SOCP with the Davis scheme may not adequately reflect the influence of non-associated soil plasticity.Nevertheless,the inclination angle of shear band predicted by mpcFEM-SOCP with the pseudo-time discrete scheme agrees well with the theoretical solution of a geotechnical system with non-associated MC soil plasticity.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgments

We acknowledge the funding support from National Natural Science Foundation of China (Grant No.52178309),the National Key R&D Program of China (Grant No.2017YFC0804602) and the Fundamental Research Funds for the Central Universities(Grant No.2019JBM092).

List of symbols

c Coefficient vector

x Solution vector

A,b Coefficient matrix and vector of linear equation

KQQuadratic cone

KRRotated quadratic cone

RmSet of real numbers with dimensionm

xjj-th component of x

u Displacement vector

u1,u2Translational displacement components in two plane coordinates

ω3Micro-rotation component

σ Stress vector

σijStress components

mijCouple stress components

ε Strain vector

εpPlastic strain

εijStrain components

χijMicro-curvature components

Δε Total strain increment

ΔεeElastic increment strain vector

ΔεpPlastic increment strain vector

∇ Differential operator

f Vector of body force

Δσ Stress increment

DeElastic stiffness matrix

CeElastic compliance matrix

L,GLamé constants

EElastic modulus

vPoisson’s ratio

GmMicropolar shear modulus

lcInternal characteristic length

fMC yield function

gPlastic potential function

cCohesion

ϕInternal friction angle

ψDilatancy angle

σmMean normal stress

h1,h2andh3Constant coefficients

εeqEquivalent plastic strain

hp(Negative) softening modulus of cohesion

tt-th pseudo-time step

λTime step factor

δDegree of non-associativity,δ=ϕ-ψ

c0Initial cohesion

ϕ0Initial friction angle

ct* Equivalent cohesion using pseudo-time discrete scheme

ϕt* Equivalent internal friction angle using pseudo-time discrete scheme

utDisplacement vector at thet-th pseudo-time step

εuConvergence tolerance

kk-th incremental step

NstepTotal number of increments

σm,kMean normal stress at thek-th incremental step

ipIndex of integration points

NiptTotal number of integration points in the entire solution domain

NσShape (or interpolation) function for stress

NuShape (or interpolation) function for displacement

t Vector of traction force

ΩSolution domain

∂ΩSolution domain’s boundary

I Index diagonal matrix

TipCoefficient matrix related to the yield function

tipCoefficient vector related to the yield function

ξipAuxiliary variable of objective function in optimization problem

Lip，ηip，sipAuxiliary variables of constraint functions in optimization problem

nelsTotal number of finite elements in mesh

leAverage mesh size

uyTotal vertical displacement in uniaxial compression test

ΔuyVertical displacement increment in uniaxial compression test

c*Equivalent cohesion using Davis scheme

ϕ*Equivalent initial friction angle using Davis scheme

θIAInclination angle of shear bands

NipYNumber of yielding integration points crossing the strength envelope

fmaxMaximum positive yield function value

uxTotal horizontal displacement in rigid wall segment

ΔuxHorizontal displacement increment in rigid wall segment

γwSoil weight