快速LZD匹配异源DEM空洞修复应用研究
李小虎,芦 颖,田 壮
中国电子科技集团公司第十五研究所,北京 100080
地形数据信息处理技术是数字地形分析(digital terrain analyse,DTA)的基础,一直以来作为测绘学、地貌学和计算机图形学的研究热点,被广泛应用于道路规划、精准农业、数字战场、实景三维等众多领域[1-2]。随着全球信息化、数字化的快速发展,作为一种重要的地理信息资源,数字高程模型(digital elevation model,DEM)产品的数据采集方式更加多元,可根据用户的个性化需求定制不同精度、形态复杂度、参考框架和覆盖范围的数据产品[3-4]。其中,机载激光雷达(airborne light detection and ranging,ALiDAR)凭借高密度、高精度的三维数据采集优势已成为获取高质量DEM的主要数据来源[5-7]。然而,受云雾遮挡、高程地形(陡峭的斜坡和深谷)和信号干扰等因素对立体成像的影响[8],导致构建的ALiDAR航测点云在某些区域散布较多的数据空洞-像素高程值为零,从而严重影响了地表数字化模拟产品的可用性[9-10]。
如何有效填补上述DEM 数据空缺,是学者们进行技术性研究任务的关键难点。目前主流方法有两种[11-13]:一是利用空缺区域邻域信息的直接插值法;二是结合三维数据融合与空间插值的综合法。改进的插值方法有:基于高斯权值-向量基(Gauss weight-vector base,GW-VB)的插值方法,在明确稀疏与稠密点云的划定界限后,能够有效提升离散点间的平滑处理效果[14];等高线间隔重差值法(contour interval redifference,CIR),该方法能够较好地捕捉到总体的地形趋势,但是由于缺乏详细的描述特征,常应用于水文区域的空缺填充[15];高精度曲面模型(high accuracy surface modelling,HASM)插值法:只需借助空缺周围数据进行填补,能够快速填补位于简单地形表面的小尺度的数据空洞[16]。改进后的自适应Kriging 插值法:能够克服离散点分布不均匀条件下所引入的建模误差,通过最优无偏估计提高插值精度[17]。
插值法在空洞范围较小且平坦的数据修复中表现较为理想,对于山脊、山谷等大面积区域缺失的情况下,常采用三维数据融合与空间插值综合法,以满足高程产品的质量要求。其中,岳国栋等[18]提出了干系数与垂直基线高度加权融合的方法,利用一组主辅影像去除侧视异常区域;李世明[19]提出了多源点云渐进配准和拉普拉斯融合算法,在面向城市三维空间精细建模中完善了局部复杂的结构表面;基于泊松融合[20]的无缝修复法,通过统计分析极大地增加了填充可用候选集,且具备复制纹理的效果;陈雪荣[21]探索出了优化后的径向基神经网络(radial basis function,RBF)方法,可有效去除大尺度噪声,并用网络预测值代替实测值有效解决非线性空洞修补;余婷婷等[22]提出的将随机森林回归算法(random forest regression,RFR)应用在DEM 空洞修补精度校正上,适用于处理各种地形异质程度的高程数据,泛化能力强。上述方法虽在去除大尺度数据空洞方面做了大量工作,但当数据分辨率较高且空洞覆盖面积较大时,海量的训练样本导致模型不易收敛,从而影响了修复效率。
本文提出了一种基于异源辅助数据的快速最小高差三维匹配算法,配合统一计算架构(compute unified device architecture,CUDA)实现GPU 多核策略并行计算,提高LZD 空间匹配模型求解和“台阶”融合算法对空洞边缘离散点平滑处理的效率和效果。修复后得到的DEM数据完整度高、过程可靠,利用该方法形成的软件成果已在工程应用中取得了较好的实效,具有一定的推广价值。
1 方法原理
1.1 LZD表面匹配原理
为了进行快速、高精度的空洞修复,首先需要统一辅助数据与待修补数据间的坐标基准,将两个结构、位姿差异的三维空间进行表面匹配。目前广泛使用的方式有最近点迭代算法(iterative closest point,ICP)和LZD 算法等[23]。鉴于待匹配两数据规则格网的地形表述特点,选用LZD 算法进行待转换空间映射模型的计算,如图1所示。

图1 空间坐标关系示意图Fig.1 Spatial coordinate relationship diagram
依据两组DEM 数据组织形式,设待匹配模型为Zc=f(Xc,Yc),其中Xc、Yc是待修复表面投影至二维平面的坐标值;同理,标准模型为Zs=f(Xs,Ys)。待修复表面上一点Pc=[Xc,Yc,Zc]T与基准数据上对应点Ps=[Xs,Ys,Zs]T间的几何关系可进行如下表示:
其中,T=[tx ty tz]T为Pc相对Ps的空间三个维度平移矩阵,s为比例缩放系数,R是含有参数θ、ϕ、ψ的表示旋转偏移的单位正交矩阵。由于DEM格网地理坐标作为一种相对坐标,不存在偏扭、弯曲等复杂情况,根据布尔莎[24]仿射变换模型得到其简化表达式如下:
式中,θ、ϕ、ψ分别为绕O-Zs、O-Ys、O-Xs轴的滚转角、偏航角和俯仰角。将式(2)带入式(1)中可建立待匹配坐标系O-XcYcZc向基准坐标系O-XsYsZs进行空间转换的矩阵模型:
其中,样本个数i=m×n,m、n分别为待匹配栅格的横、纵坐标像素量。依据最小二乘(ordinary least squares,OLS)迭代估计方法,取Z方向高差平方和最小值建立目标方程。则最小高差极值的计算公式为:
存在平面同名点时,格网值的权重因子wsi=1,否则wsi=0。当基准与待匹配数据分辨率不一致时,利用双线性插值法(bilinear interpolation,BI)进行重采样,构造j个离散的虚拟像素pfj(xj,yj,zj),其中zj=0。
将局部虚拟空间近似为连续二次线性曲面:
通过4 个临近参考点确定横纵两个维度的曲线参数a0、a1、b0、b1,将pfj带入式(5)计算等距插值zj=hfj(xj,yj),将数据修改为相同尺寸。
利用最小二乘迭代求解(4)中E接近限差时的7个约束方程参数,从而构建三维匹配的空间坐标转换模型。
1.2 台阶融合
受不同时相、传感几何辐射差异等因素的影响,空洞衔接边缘会产生不可避免的高程值突变[25],针对存在的“台阶”式拼接缝,利用图像融合技术对其进行平滑处理。
经台阶融合算法处理得到的高程坐标Zfusion,是根据其自身每个格网处的高程值Zdem与同名点高程值Zref按如下规则加权平均得到:
式中,pdem表示待处理DEM 数据点的权重,与其对应的同名参考点权值之和为1。结合离散图像相邻区域像素值变化小于区域内部的特点,可利用栅格距离衰减规律对每个格网处的pdem进行计算。
若取窗口大小为n×n,中心点权重p(xc,yc)=0.5,其余8个方向n2-1 个点的权重和之为0.5,则待修复数据邻域内各点的高程梯度倒数绝对值为:
式中,像素偏移量i、j∈[0,n-1],且i、j不同时为0,若Zdem(xc+i,yc+j)=Zdem(xc,yc),则gdem(xc,yc,i,j)=0。
以待修复点作为掩模中心进行加权邻域求梯度平均,可得到待处理高程权值系数:
将pdem带入式(6),经台阶融合输出空洞填充边缘的高程坐标信息,使格网像素能够自然、平滑地衔接在一起。
实现过程如下:
(1)设定每个格网点初始化的权值p0如下:
i、j分别为DEM数据的行号和列号,有效初值为215,为确定待修复点的高程权值分布,需要对图像顺序、逆序两次进行计算。
(2)定义一个偏移量offset:取(各方向)权值重新计算的格子数默认为20。
(3)以栅格平面的左上角点作为原点,行号、列号依次递增,遍历寻找空洞边缘点,取该像元邻域内左、左上、上、右上方向上各offset∈[1,(n-1)/2]个点并根据梯度计算依次设置权重。
(4)更改原点为像平面右下角,行号、列号依次递减,在左下、下、右下、右方向上逆序重复上述操作,更新上一步重新计算的像元的权重pdem=min{p(xc,yc),pdem} 。
(5)取满足pdem(x,y)<1 的所有点,利用加权平均的方法重新计算高程值,以消除待修复数据存在的台阶问题。
2 快速DEM空洞修复方案
考虑到大尺度数据空洞修复时存在的实时性问题,首先,基于LZD 原则将表面匹配中三个维度的残差分析简化为取Z 方向极小值,进而利用GPU 并行处理机制,将同名点搜索和格网点像元值的填补过程分解至多个线程块同步进行,以缩短处理过程的总体运算周期。
2.1 匹配模型参数获取
为了得到最优的表面匹配结果,通过最小二乘迭代逐步优化模型数值,确定各参数近限差的增量矩阵dX。对变换阵Trans的7 参选取初始值X0=[R0,t0,s0]T,其中令Rψ0、Rϕ0、Rθ0、tx0、ty0、tz0=0,s0=1 表示空间两坐标系重合,无相对旋转、平移,默认等比例缩放。
遍历待匹配样本中的每个高程点Pci=[Xci,Yci,Zci]T,带入式(3)进行Trans变换后,在标准DEM中寻找格网坐标满足xci=xsi、yci=ysi的同名点Psi。
当同名点不存在时,本算法中使用了双线性插值构造虚拟同名点的高程坐标,数据量小时也可考虑反距离加权平方(inverse distance weight,IDW)算法。
给定一个足够小的步长delta,当前点在X、Y方向的一阶导数计算公式如下:
式中,待匹配所有点满足Zc=f(Xc,Yc)。对误差函数e(x,y)进行一阶泰勒展开,得到线性化误差函数:
每次迭代各点误差函数的过程就是求最优增量参数矩阵dX*的过程:
经系数反推,可建立增量方程组B=AdX,设计观测系数矩阵Ai=[dzxdzy-1]T,得到Bi:
将Ai*Bi的结果存储到A矩阵的第i行,Zci-Zsi的值存储到B矩阵的第i行。
遍历结束后,使用奇异值分解(singular value decomposition,SVD)方法解超定方程以计算dX增量:
并将dX*累加到变换矩阵中X=X+dX*,如果dX小于迭代限差Vx或达到最大迭代次数Va时,跳出迭代过程完成参数计算。
在匹配过程中,迭代终止条件由各参数相邻迭代值之差来判定,即七个转换参数的增量,七个转换参数的限差值和设定的最大迭代次数由各个观测值的精度决定。
匹配模型参数获取的具体流程如图2所示。
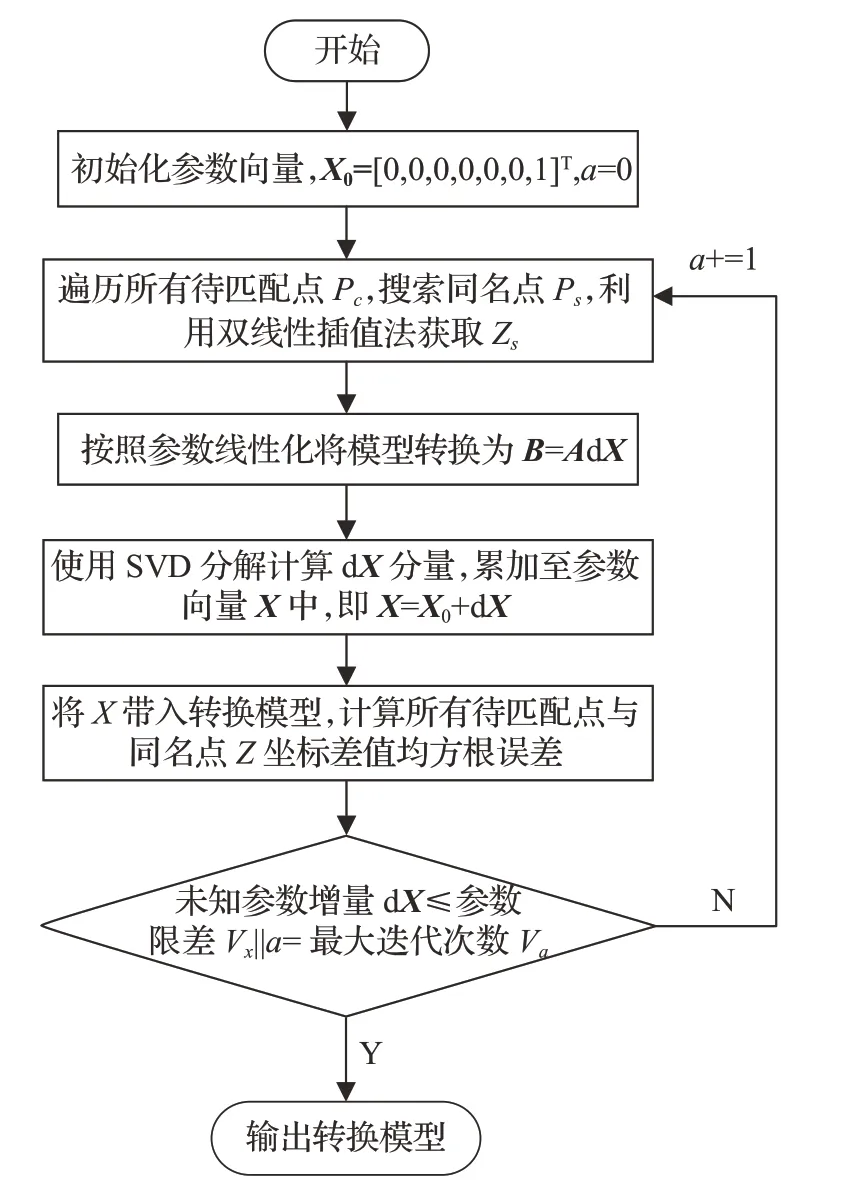
图2 算法流程图Fig.2 Algorithm flow chart
2.2 空洞修复任务的GPU并行方案设计
引入最小高差算法虽然避免了三个维度最小距离计算造成的冗余问题,但在进行同名点搜索、邻域加权时,穷举式的距离查找过程和大规模的DEM 数据量依然影响了空间匹配的算法效率。
因此,加入GPU并行处理技术,通过PCIe总线协助CPU 进行运算控制操作,充分发挥CPU 的复杂逻辑控制能力和GPU在处理图像高密集计算和超长流水线任务的结构优势,形成的CPU-GPU异构模型如图3所示。
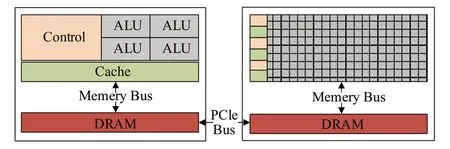
图3 CPU-GPU异构模型Fig.3 CPU-GPU heterogeneous model
NVIDA 推出的标准运算平台CUDA,代码层面更易编写,在性能、成本维护方面表现突出。本文利用其并行计算特性,提出一种多核多线程并发的DEM 匹配修复方案。其中,并行化编程最需考虑的线程同步和数据归并问题,利用CUDA平台线程调度和内存的访问管理原则,将空洞修复计算过程以核-格网-线程快-线程(KERNAL-GRID-BLOCK-THREAD,KGBT)的三级组织架构进行调度配置。
构造顺序的处理逻辑步骤如下:
(1)获取所有待匹配格网像元同名点坐标值;
(2)迭代计算残差极值并求解空间映射模型的特征向量;
(3)利用加权融合算法重新计算空洞边缘高程坐标。
获取同名点坐标和加权融合过程需要进行大量重复计算,因此分别映射至knl_search、knl_restore 两个核函数中,并采用单指令多数据流(single instruction multiple data,SIMD)以异步的形式执行相同的算法指令:
首先,以程序初始化和影像数据GeoTiff(tiff),Erdas Imagine Images(img),ASCII DEM(dem)等格式的解析作为起始模块。利用GDAL(geospatial data abstraction library)库读取元数据和高程信息数组取至主机端内存。
针对基准模型大小远大于待匹配区域的现象,利用OpenCv库对存储DEM的数据模型文件进行裁剪处理,调用RasterIO 将大图分割为512×512 大小的块后,将栅格数组与元数据一同拷贝至全局显存(gloabl memory,GM),完成程序的初始化。
设置临近点计算的辐射距离为0.2 m,采用CUDA编程模型并调用核函数knl_search,以线程id 作为检索项,将遍历像点的任务映射成若干并发执行的子任务。在某一线程网格(Grid)的多个线程块(Block)中对区域分割后的子图进行同名点搜索,利用异步流迭代方法将同名点对应的坐标集合存储至当前Block(32×32)的共享存储器中,供块内线程共用,减少访问延迟以提高读写效率。在knl_search计算模型中,对于每个线程,分别搜索当前待匹配格网距离相近的所有点,最近距离小于等于阈值时确定为同名点对。同名点不存在时,设置横纵缩放比例和几何中心利用BI 插值函数构造虚拟点,resize调整数据至相同尺寸。待所有样本完成查询操作后,输出参数控制所有点对信息进行坐标反算。
迭代求解映射参数向量的过程,是采用奇异值分解(singular value decomposition,SVD)对稠密矩阵进行降维,其计算代价大,但由于运算先后关联性较强,内部逻辑耦合度高,不适合进行并行化改造,因此该矩阵运算仍在CPU串行域中进行。
待模型数据解析完备,针对图中多个待修复区域进行的8邻域权值计算,并将多个空洞分配给多个线程块block同步进行“台阶”融合。正、逆遍历所有待融合点,计算中心点p(xc,yc,zc)与邻域各点高程权重关系。对拼接边缘像素进行平滑处理,以函数返回值形式合并修复后数据至CPU内存,将结果模型写入输出的DEM文件中,完成空洞修复运算。
任务基本设置:
(1)分配2个顺序进行的核函数(kernel),进行同名点插值计算和台阶像素融合。将knl_search函数设置为逐点搜索,n个点对应n个线程。等待图像所有点遍历结束,通知主线程迭代求解单应性矩阵;对于knl_restore函数,若相邻Z坐标缺失个数>1,即判定为待修复空洞,采用流水线作业实行多个空洞边缘并发修复。
(2)knl_search 的m个子图分别对应m个格网,将格网划分为多个pixel 的线程块(block),每个线程块分别对应256个CUDA线程。
(3)子图中第k个空洞映射至knl_restore 的第k个线程块中。
采用程序并行化关键解决的几点问题:
(1)在大样本点集查询任务中,采用K近邻法(Knearest neighbor,KNN)查询单元格间的拓扑关系,通过两步法确定法向最小距离点。KNN算法的搜索过程可有以下三种常用方式:穷举法、kd树(k-dimensional-tree)和球树(ball-tree),根据预测平均时间随样本数量变化曲线知[26],穷举的方式更适用于容量较大的DEM数据。
(2)设Q为大小为u的n维参考点集,R为大小为v的查询点集,通过线性扫描对k个最近邻域点进行表决。表面匹配算法只关心距离最小点的坐标值,在此基础上,对v个长度为k点集的分别进行插入排序。这种暴力实现的方式非常耗费运算资源,而结果集合的搜索与有序表的生成在匹配点之间不存在任何依赖关系,因此,可充分利用GPU 编程将遍历格网数据进行同名点查寻询的任务映射成若干并发执行的子任务,提高算法效率。
(3)融合算法是根据所有点邻域加权取均值,进行Z坐标平滑。这一过程在程序中,遍历待修复DEM 所有点获取权重是独立且高重复性的,因此将任务分配至GPU运算单元重叠执行,在并行层面分别对所有待处理点高程进行重算,将循环遍历的过程原子化,显著降低了内存占用和运算时间。
CPU并行架构下,设3维参考点集Q的样本数为待匹配栅格大小i×j,查询点集为v,由于核心较少导致能够同时开启的线程数目有限,可得邻域搜索的时间复杂度为O(ijuv)。结合图形处理单元加速运行该算法,每个样本单独开启一个核函数同步处理,在相同数据量的情况下,时间复杂度减少至O(uv)。然后,对于搜索到的临近点集,进行v个长度为k的插入排序,该操作的时间复杂度为O(vk2),使用GPU 并开启v个线程并行执行可将时间复杂度降低为O(k2)。在边缘平滑算法的优化中,逐点高程值重算被简化为同步进行的窗口(n×n)卷积,计算时间缩短样本个数倍,时间复杂度为O(n2)。从算法理论角度分析该策略具备明显的优化性能,而系统实际运行的总时长,不仅需要对算法执行指令的条数进行评估,还涉及到了线程工作量后的步骤复杂度。
图4 为GPU 多核架构与多线程作业下的具体实现流程。

图4 GPU多核多线程空洞修复程序流程Fig.4 GPU multi-core multi-thread hole repair program
3 实验内容
3.1 实验数据及平台
本文选取的基准数据来源于奋进号航天飞机的雷达地形测绘(shuttle radar topography mission,SRTM)数据,全图数据包含1 200×1 200个采样点高程值,水平和垂直精度分别为±20 m和±16 m,格网间距90 m(3″),投影基准采用WGS84 坐标系统,经纬范围(102.4 E~104 E,29 N~30.3 N)。待修复数据均为中国境域采集的SRTM-DEM 30数据,格网间距30 m(1″)。
分别对待修复数据中海拔较高的青藏高原(区域1)和地势相对平缓的长江三角洲冲积平原(区域2)的山脊数据缺失和条状云层遮挡进行算法验证,其中区域1空洞占比4.5%,连通空洞个数为8;区域二占比2.2%,空洞个数为4。
实验环境:软件平台采用Visual Studio2010和C/C++语言进行软件设计与编译,通过观测模型的收敛速度、修复总耗时、加速比等,在搭建的三个异构混合平台上依次进行对照组实验,以验证本文方法可用性和实现效率。工作站所用处理器(CPU)及显卡(GPU)型号说明和预先设置匹配模型收敛条件分别如表1、表2所示。

表1 CPU/GPU参数Table 1 CPU/GPU parameters

表2 空间映射模型7参增量限差Table 2 Seven parameters for spatial mapping model
根据两个DEM(或DSM 等)的元数据信息,设定Geotiff格式数据点平面的坐标。以标准DEM的左上角点作为原点Os(0,0),Xs(行)方向每行间隔为经度方向分辨率×111 000 m,Ys(列)方向间隔为纬度方向的分辨率×111 000 m。待匹配DEM 数据设定为Os(0,0)-XcYc原理同标准数据。
在修复前进行数据准备:
(1)将待匹配DEM数据用GDAL库读入内存,包括元数据信息和高程数组;
(2)将标准DEM中对应待匹配DEM区域(略大)提取为算法中的标准DEM;
(3)根据精度需求进行异源数据等间隔采样;
(4)切分地形区域为若干(m)子图;
3.2 实验结果与分析
LZD 算法的模型解算精度取决于各参数限差和迭代次数,鉴于两组地区地理面积相近,此处均采用最大迭代次数300,采样大小500×500 pixel。当所有参数增量满足迭代限差时,算法终止,并确定模型参数向量。
分别取待匹配DEM 中青藏高原山区、长江三角洲冲积平原两组典型的数据模型作为对照组进行格网数据空洞修复,以验证该方法在不考虑实现策略时,不同地势条件下算法的可行性。其中,青藏高原地区地势变化较大,受传感范围限制,在数据的采集和重构过程中易丢失高海拔山脊处的三维信息;长江三角洲平原位于长江入海口,该地区平均坡度较小,但由于厚云遮挡导致内含两条狭长的数据空缺。两组待修复数据大小均为26 MB,全国基准DEM 大小为5 GB,经模型求解和高程坐标估值计算后,得到修复后的结果如图5所示。

图5 漏洞修补对比图Fig.5 Comparative diagram of vulnerability patching
由图5可知,对于两地区分布的不规则空洞的修复效果表现为:均能够较好地恢复局部纹理特征、几何性质稳定,在源数据的基础上保持现有分辨率,并扩大了数据的空间覆盖,实现了影像质量的有效提升。
在尽可能保证精度的前提下,取区域1的数据进行计算性能测试。分别采用CPU多线程和CUDA多线程调度策略,设置大小相同的数据区域(区域1)和采集密度(500×500 pixel),依次记录模型的匹配耗时与空洞修复总耗时。配备的三组硬件实验环境为,平台1:CPU为Xeon CPU E3-1230V6,显卡采用NVIDA GeFouce GTX 980;平台2:CPU 为Xeon CPU E3-1230V6,显卡采用NVIDA GeFouce GTX 1080 Ti;平台3:CPU 为Intel Core i7-7700,显卡采用NVIDA GeFouce GTX 1080 Ti。在多种主机设备组合配置下,对照并行算法的执行效果。
实验结果表明,部分任务调用CPU-GPU 异构的CUDA 编程模型进行实现后,修复总时长<0.86 s,具体运行效率如表3所示。
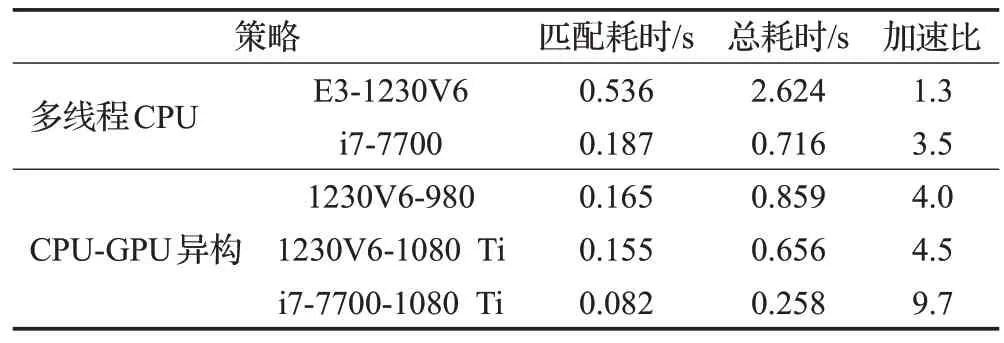
表3 不同策略下区域1修复耗时与加速比Table 3 Time-consuming and speed-up ratio of Region 1 repair under different strategies
采用GPU 技术协助CPU 处理重复计算,缩短了点对最优距离计算和排序时间,然而随像素尺寸增加数据在CPU-GPU 间拷贝的开销增大,扩容后的多线程CPU策略(平台2)较平台1 总耗时明显缩减,且匹配耗时占比由20.4%增加至26.1%,串行优势在充足内存容量条件下更为显著,同时,并行计算效率也提升了3.6倍。平台1与平台2采用相同CPU和相异的图形处理器,利用并行异构策略,使总执行加速比分别提升至4.0 和4.5,优化后的匹配、融合耗时较CPU 多线程最多可减少71.082%和76.006%。在平台3上运行异构程序,算法总体修复的执行效率相较于单线程CPU 能够达到9.7 倍以上的加速比,具有较好的修复性能。
为了检验本文算法在不同地形场景下的匹配精度,分别将待修复数据中的区域1和区域2与全国基准数据进行LZD 三维匹配。其中,青藏山区和冲积平原数据大小为各取50 个点作为测试样本,与基准数据对照计算Z坐标估值残差,得到的最小参数增量、误差矩阵和Z方向精度均方误差(单位:m)如表4所示。

表4 迭代最终参数增量与误差Table 4 Iterate over final parameter increment and error
以区域1的山脊为例,可看到模型计算的高程值在空洞边缘存在“台阶”形断层,为完善修复效果,对该空洞区域进行了加权融合。取空洞边缘点Z坐标值得加权平均,进行DEM高程值重算,再次赋值后达到奇异点去除和边缘平滑的效果,空洞平滑修补前后对比如图6所示。

图6 空洞平滑修补前后对比图Fig.6 Comparative diagram of cavity before and after smooth repair
如图6(a)所示,融合前的高海拔数据缺失面,边沿分布着非连续的像素条带,在数据准确度和视觉效果层面都存在明显缺陷。经加权融合纠正后的该区域见图6(b),保留了主要地形特征,未见明显修复痕迹,达到趋近于基准数据的完善要求。
4 结束语
机载雷达(airborne radar,AR)在高海拔、崎岖地势和极端气候时出现的测绘盲区,导致衍生出的数字高程数据(DEM)存在数据空洞等的问题,现有的空间插值和表面匹配算法为该空缺修复研究提供了有力支撑。为了进一步满足准确、高效的应用需求,本文提出了一种改进的快速LZD三维匹配算法结合“台阶”融合的修复方法。借助异源辅助数据,在搭建的不同平台下,分别对2 组差异明显的非结构化地形样本进行了方法验证。实验结果表明本文采用的方法,修复后的图像信息丰富、空洞边缘平滑,误差控制在±37.725 m,符合地形数据的处理需求。在模型精度满足固定限差的条件下匹配效率成倍提升,较CPU 多线程架构运行耗时可减少76%,加速比最优可达9.7倍,在大尺度数字高程模型修复领域具有明显优势。

