群智能算法优化XGBoost的信贷风险预测

朱丽华，龙海侠

1.安阳工学院 计算机科学与信息工程学院，河南 安阳 455000

2.海南师范大学 信息科学技术学院，海口 571158

随着经济的发展，信贷风险预测成为研究热点，国内外学者都进行了深入研究。海量高维数据的积累，提升了机器学习进行信贷预测的准确性，极端梯度提升（extreme gradient boosting，XGBoost）算法[1]被广泛应用于该领域并取得了较好的效果。常规的XGBoost 集成模型具有参数过多，计算复杂等特点，因此优化模型参数具有重要的意义。文献[2]采用XGBoost和RF进行个人信贷风险预测；文献[3]利用强化学习优化XGBoost信贷风险预测；文献[4]利用粒子群优化XGBoost 进行银行个人信贷风险预测。

由Xue等[5]于2020年提出的麻雀算法（sparrow search algorithm，SSA）是一种新型群智能优化算法，表现出了较高的寻找最优解能力。与大多数智能优化算法相比，SSA具有在迭代后期容易陷入局部最优，仍存在收敛精度低问题。为提高麻雀算法的全局寻优能力，科研人员提出了不同的改进策略：吕鑫等[6]引入混沌映射初始化种群帮助个体跳出局部最优；张伟康等[7]引用了黄金正弦进行位置更新，既提高了全局寻优又增强局部搜索能力；李爱莲等[8]引入了柯西变异策略，提高了全局搜寻能力，防止早熟现象发生；毛清华等[9]融合柯西变异和反向学习，扩大搜寻领域，改善全局寻优；张晓萌等[10]融合多策略来扩大寻优范围，避免陷入局部最优。近年来，随着群智能优化算法不断完善，SSA 被广泛用来优化模型。王海瑞等[11]将改进的麻雀搜索算法应用在分布式电源配置中，大大降低了配电网有功损耗与电压变差；陈深等[12]将改进后的麻雀算法应用在天波雷达定位中，实现了快速定位，且提高了定位精度。

综合目前研究现状，本文对传统的SSA算法进行改进，提出一种改进麻雀算法（sparrow search algorithm based on golden sine search，Cauchy mutation and opposition-based learning，GCOSSA），用来优化XGBoost模型进行信贷风险预测。GCOSSA 采用黄金正弦搜索策略，有效平衡全局和局部搜索能力；在算法中引入反向学习策略和柯西变异进行扰动来扩大搜索领域改善陷入局部最优，同时采用贪婪规则确定最优解。采用改进后的GCOSSA 算法优化XGBoost 参数，提高了模型识别信贷风险的准确率。

1 相关算法原理

1.1 XGBoost算法

XGBoost 是一种基于梯度提升树实现的集成学习模型，由于其对目标函数进行二阶泰勒展开，保留了更多有效信息，在分类与回归问题上具有较高的精度。XGBoost的集成模型如公式（1）所示：

式中，xi是输入的第i个特征向量；表示预测值；K表示回归树的数量；R是回归树的集合空间；fk表示集合R上的一个函数，用来表示基学习器的输出。

累加迭代过程结果，得到XGBoost的目标函数：

进行泰勒展开和求导，得到目标函数：

式中，γ为惩罚函数系数；T为k次迭代后树中叶子节点个数；λ为正则化惩罚项系数；Gj表示当前叶子节点所有样本一阶导数和；Hj表示当前样本所有二阶导数和。

XGBoost在分类与回归问题上具有较高的精度，本文使用XGBoost构建模型进行信贷风险预测，并使用改进的麻雀算法优化其参数。

1.2 麻雀搜索算法

麻雀搜索算法（SSA）是一种新型的群智能优化算法，在每次迭代的过程中，发现者的位置更新公式如下：

加入者的位置更新公式如下：

式中，XP表示发现者占据的最优位置；Xworst为当前全局最差位置；A表示随机分配元素为1或者-1的一个1×d矩阵，满足式子A+=AT(AAT)-1。

警戒者的位置更新公式如下：

式中，Xbest是当前全局最优位置；β是步长控制参数满足均值为0，方差为1 的正态分布；K为随机数取值范围[-1，1]；fi为当前麻雀的适应度值；fg为当前全局最佳适应度值；fw为当前全局最差适应度值；ε是最小常数。

1.3 改进的麻雀搜索算法

传统SSA算法中发现者个体都按照公式（4）进行位置更新，没有充分发挥个体位置的优势，算法容易早熟收敛陷入局部最优。本文采用黄金正弦[13]搜索策略，使得种群中的个体既能够远离其自身位置进行探索，增强全局搜索能力；又能在黄金分割系数确定的位置附近区域进行搜索，增强局部搜索能力。黄金正弦搜索策略位置更新公式：

使用黄金正弦搜索策略改进[14]后的发现者更新公式：

为了让个体扩大搜索领域[15]寻到最优解，在算法中引入了反向学习策略[16]，表达式如下：

式中，itermax是最大迭代次数，t为迭代次数。

在最优解位置中引入柯西变异[17]进行扰动更新，改善陷入局部最优，提高算法获取全局最优解能力。更新公式变为：

式中，cauchy(0,1)为标准柯西分布函数；⊕表示相乘含义。

为提升算法寻优性能，采用动态选择策略，将反向学习策略和柯西变异扰动策略[18]在一定概率下交替执行，当随机生成数小于选择概率p进行反向学习策略位置更新；否则进行柯西变异扰动。p公式为：

式中，w1、w2取值0.5和0.1。

同时引入贪婪规则，比较新旧位置的适应度值，确定最优值位置，公式为：

算法流程：

步骤1初始化麻雀种群，设置种群大小，最大迭代次数，发现者比例，警戒者比例，警戒值，安全阈值；

步骤2计算适应度值并对麻雀位置排序，确定当前最优、最差适应度个体；

步骤3根据式（8）更新发现者的位置；

步骤4根据式（5）更新加入者的位置；

步骤5根据式（6）更新警戒者的位置；

步骤6根据式（12）选择反向学习策略或柯西变异扰动对当前最优解扰动，产生新解；

步骤7根据式（13）确定是否进行最优解位置更新；

步骤8判断是否完成迭代次数，若满足，则执行步骤9，否则跳转继续执行步骤2；

步骤9输出最佳位置和最优适应度值。

2 融合GCOSSA算法的XGBoost预测模型

XGBoost 模型的参数影响着模型的效果和计算代价，参数learning_rate过小影响运行速度，过大则影响准确率；调控参数max_depth 即树的最大深度控制过拟合；优化参数n_estimator 得到最大的迭代次数；优化参数gamma 得到节点分裂所需的最小损失函数下降值，实现合理分裂节点。本算法中实现了对上述四个参数的调控达到优化模型性能。首先使用GCOSSA 算法初始化XGBoost 参数，传递粒子的位置参数，然后计算适应度并排序，更新个体位置，记录全局最优。满足迭代次数后结束遍历，并输出最优解即最优麻雀位置，传给XGBoost模型最优参数，最后重新训练XGBoost预测模型。算法流程如图1所示。

图1 算法流程图Fig.1 Flow chart of algorithm

3 实验结果与分析

3.1 实验环境和数据集

数据集采用UCI网站上信贷数据集GCD和ACA，数据集描述见表1，所有数据集采用70%为训练集，30%为测试集，并对数据进行随机划分。实验环境为Anaconda3下的Jupyter Notebook，编程语言采用Python，操作系统Win10，电脑内存8 GB，CPU为AMD A10-7300。

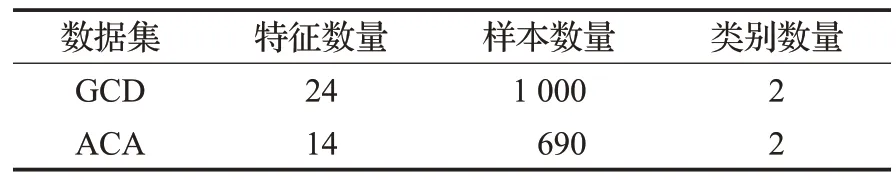
表1 数据集基本信息Table 1 Basic information of datasets

3.2 GCOSSA算法性能测试

采用6个标准测试函数对SSA及本文改进的GCOSSA算法测试，进行性能对比，发现者占比0.2，警戒者占比0.1，安全阈值ST为0.8，种群数量30，纬度10，迭代次数300，测试函数如表2 所示。经典SSA 及本文改进后的GCOSSA算法性能对比如图2所示。

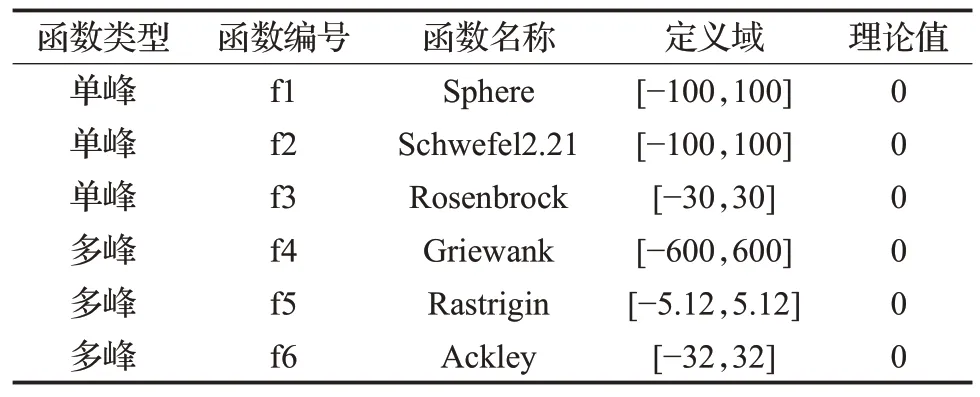
表2 基准测试函数Table 2 Benchmark test functions

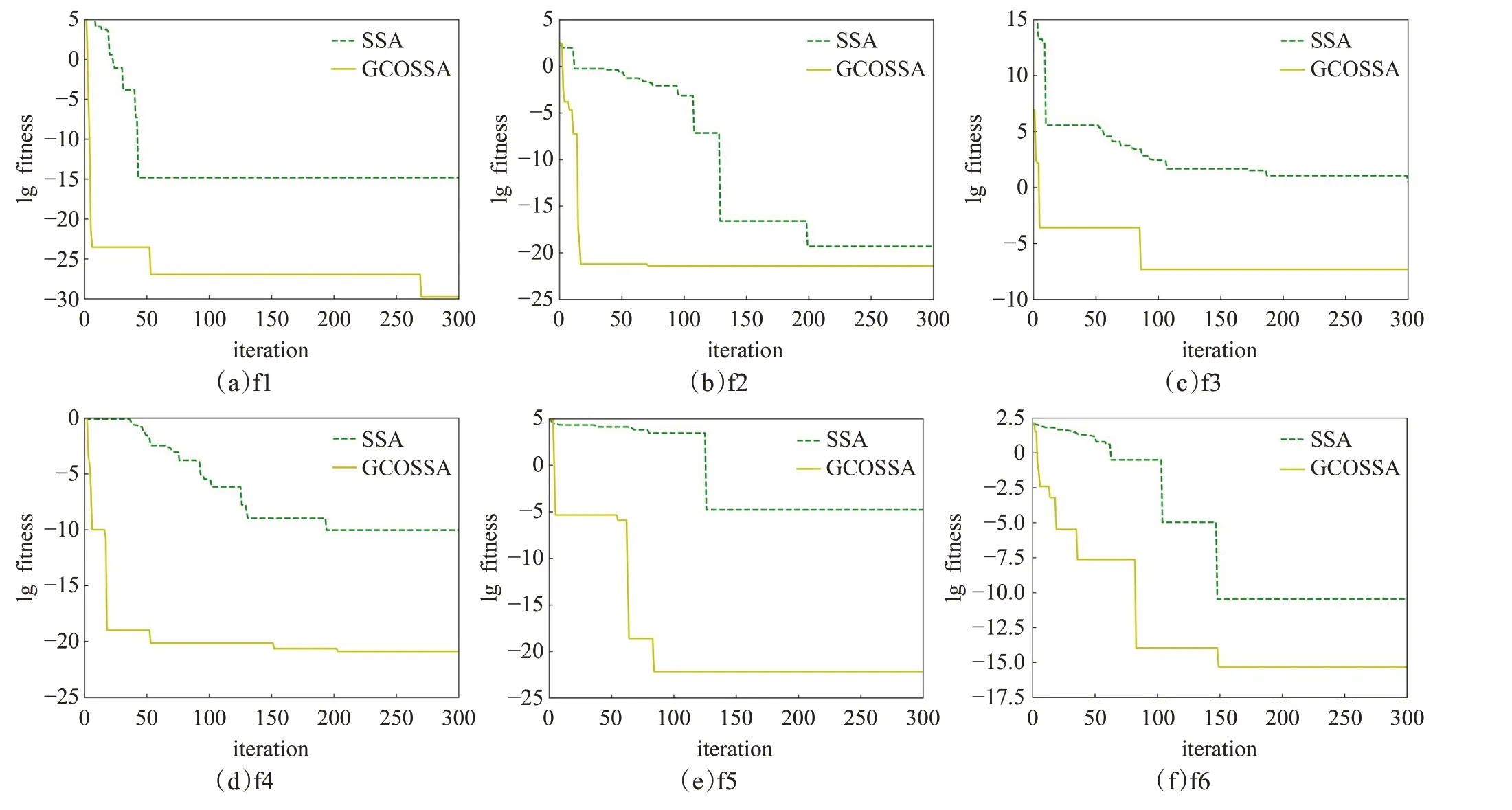
图2 收敛曲线Fig.2 Convergence curve

对图2 中6 个测试函数运行结果图进行分析，横坐标表示更新次数，纵坐标表示以10 为底的适应度值的对数。对比图中曲线可以看出，GCOSSA曲线对数值更低，因此寻优精度较SSA 更高；GCOSSA 曲线出现拐点更早，因此较SSA 求解速度更快。GCOSSA 性能优于SSA算法，在于发现者采用黄金正弦搜索策略同时增强了全局和局部搜索能力，在最优解位置根据选择概率p进行反向学习策略位置更新或柯西变异进行扰动更新，有利于避免陷入局部最优，寻找到全局最优解。

进一步评估SSA和GCOSSA算法性能，对6个测试函数进行求解，算法分别独立运行50次，性能测试使用平均值mean和标准差std，平均值越小表明算法具有更好的寻优精度，标准差越小表明算法寻优更稳定，具体性能评估值如表3所示。

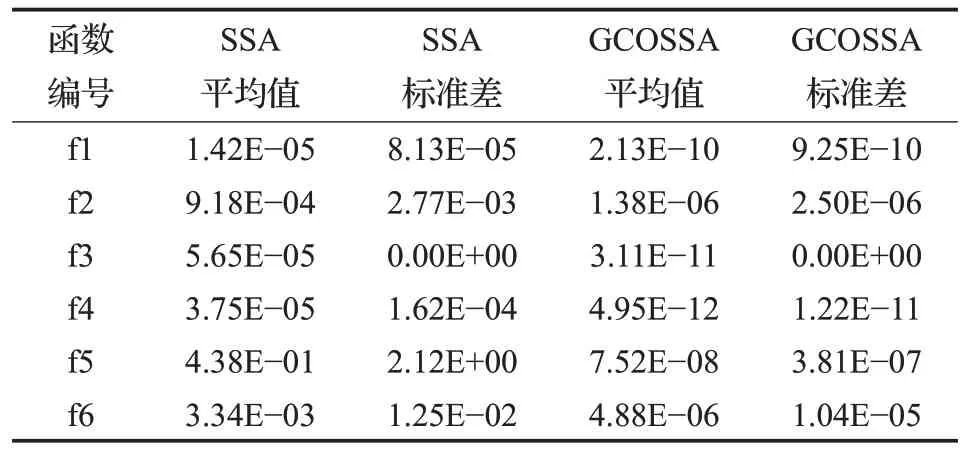
表3 GCOSSA与SSA算法性能Table 3 GCOSSA and SSA algorithm performance

对表3 进行综合分析，对于单峰函数1 和函数2 两种算法都得到了理论最优值，但GCOSSA 算法平均值和标准差较SSA算法提高了多个数量级，说明具有更高的收敛精度且寻优结果更稳定；函数3虽然没有得到理论值，但同样提升了收敛精度；多峰函数4、函数5 和函数6都达到了理论最优值，且平均值和标准差都有明显数量级的提高，寻优精度更高及稳定性更好。无论单峰函数还是多峰函数，GCOSSA算法较SSA算法在平均值和标准差上均具有数量级的提高，具有更高的求解精度。从平均值和标准差指标总体上看，GCOSSA 算法的值更小些，表明其全局寻优要优于SSA 算法且稳定性更高。

3.3 GCOSSA算法优化XGBoost参数进行预测与分析

采用UCI 上的GCD 和ACA 数据集进行风险预测，通过网格搜索GridSearchCV、SSA、文献[19]改进后的麻雀算法ISSA和本文改进后的GCOSSA方法对XGBoost参数进行优化。在GCD 数据集上对应最佳参数如表4所示。

表4 数据集上参数值Table 4 Parameter values on datasets

为验证实验准确性，以ROC 曲线和AUC 面积作为评价指标。以真正率（sensitivity）为纵坐标轴，代表分类器预测的正类中实际正实例占所有正实例的比例。假正率（false positive rate）为横坐标轴来绘制ROC曲线，代表分类器预测的正类中实际负实例占所有负实例的比例，常表示为1-specificity。ROC 曲线越靠左上角说明算法准确率越高。AUC 值为ROC 曲线下的面积，值越大说明模型性能越好。

图3和图4分别是XGBoost模型融合上述四种不同寻参方法在数据集GCD和ACA上的ROC曲线和AUC值。从图中可以看出采用GCOSSA算法的AUC值均高于其他算法，表明改进算法预测准确率最高。

图3 GCD上ROC曲线Fig.3 ROC curve on GCD

图4 ACA上ROC曲线Fig.4 ROC curve on ACA

在不同数据集上采用不同算法优化XGBoost参数，算法性能对比如表5，评估指标准确率和时间，采取10次实验平均值。基于GridSearchCV 网格搜索的XGBoost用时较短，SSA、ISSA和GCOSSA算法通过改善发现者更新求全局最优，因此时间较长，但是由于GCOSSA采用黄金正弦来更新发现者，同时按照选择概率进行反向学习或柯西异或，提高了全局搜索同时避免陷入局部最优，算法准确率更高，优化算法运行时间较SSA 和ISSA长。

表5 算法性能对比Table 5 Comparison of different algorithms

4 结束语

XGBoost 广泛应用于信贷风险预测，其参数数量大，且不同参数值对预测准确率影响巨大。智能算法广泛应用于参数寻优，针对SSA算法在迭代后期容易陷入局部最优，本文提出了一种GCOSSA 改进算法，选择UCI中的两个信贷数据集，通过对比GridSearchCV搜索参数、SSA及ISSA寻优参数，验证了GCOSSA寻找参数最优，预测模型具有更高的准确率。下一步将继续改进加入者飞行模式提高模型寻优性能，研究XGBoost 算法，并将其应用到更多领域。