一类含摩擦项的群聚模型的动力学探究
王 杰
吉林建筑大学 基础科学部,长春 130118
0 引言
奇异摄动问题是一类微分方程问题,在所研究的方程中会带有“小参数”进行干扰.早在19世纪末期,诸多学者就已关注到这类问题.另外,在自然界中,人们会观察到动物种群常常会排成特殊队形前进的现象,这种现象可以客观解释为在某种规则下,很多个体在无中心指导状况下达成某种一致状态,然后有组织地进行一种有序运动.实际上在数学领域,这一现象称为Flocking(群聚)现象[1-4].近年来,很多来自不同领域的人们都在研究Flocking现象,研究对象有鸟类、虫类、人群等,并且该现象在工程中得到广泛应用.
描述Flocking现象的模型有很多,其中有一类建立在牛顿力学系统中,将粒子的线速度进行耦合,最后给出一个限定条件后会达到一种渐近flocking状态,这类模型就是著名的Cucker-Smale(C-S)模型.近年来,文献[5-6]考虑了一类带有Rayleigh摩擦项的Cucker-Smale模型,然后文献[7-9]又利用奇异摄动理论讨论了一类Flocking问题.本文是在此基础上针对C-S模型加入Rayleigh摩擦项和小参数进行扰动,最后利用动力学系统理论和奇异摄动理论初步分析相关动力学问题.
1 预备知识
1.1 快-慢系统
主要介绍快-慢系统[7],并对系统的快变体系进行分析.
具体考虑快-慢系统

(1)
满足初值
U(0)=U0,t=0
(2)
其中,F(U),G(U):RN→RN都是连续函数.做时间尺度变换
则
故有
当
ε→0
分别得到
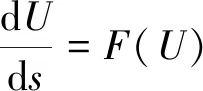
(3)

(4)
称F(U),G(U)分别为式(1)的快变体系和慢变体系.
2 Cucker-Smale多尺度模型
2.1 多尺度问题
考虑如下多尺度问题

(5)
满足
(xi,vi)(0)=(xi0,vi0), 1≤i≤N
(6)
其中,ψ(S)>0,S=‖xj-xi‖≥0, 0<ε≤1, 1≤i,j≤N
其中,非负对称函数ψ(S)表示粒子之间的交流权重,即ψ(S)是关于第i个粒子和第j个粒子的影响函数,要求ψ(S)连续可积且有界.
令
以及
则式(5)可写为:

(7)
做时间尺度变换
所以,
故
令
ε→0
得到:

(8)

(9)
对于方程,可写为
进一步,可记cij=ψ(‖xj-xi‖)有界,因此快系统式(8)改写成:

(10)
2.2 快系统的有界性
定理2.2.1 设(xi,vi)∈R2d为式(10)满足初始条件的解, 则有:
‖xi(s)‖≤C
‖vi(s)‖≤max{‖v10‖,…,‖vN0‖,1},s≥0, 1≤i≤N
其中,C为仅和x(0)=[x10,x20,…,xN0]T相关的常数.
证明 首先,由
所以xi=xi0,因此一定存在一个只和x(0)相关的常数C>0,使得‖xi(s)‖≤C,下证vi(s)是有界的,
若存在i∈{1,…,N},使得‖vi0‖>1,则
不失一般性,不妨设∀j≠i,且‖vi‖>1,‖vj‖<‖vi‖,故有:
(vj-vi,vi)=(vj,vi)-‖vi‖2≤‖vj‖‖vi‖-‖vi‖2<0
此时有
所以‖vi‖2随时间s递减,且有‖vi(s)‖<‖vi0‖,从而若存在i∈{1,…,N},有‖vi(s)‖≤max{‖v10‖,…,‖vN0‖},s≥0,1≤i≤N.
综上,得证.
3 结论
本文运用奇异摄动理论和动力系统理论, 初步分析了一类含有小参数和Rayleigh摩擦项的Cucker-Smale模型的解的有界性,有界性对于解而言十分重要,是讨论最终能够得到渐进群聚解的前提条件,可为以后探究此模型的其他动力学性质提供参考.

