在“说”中发展在“说”中提升

王杰

摘要：为了提高学生参与课堂的积极性，激发学生内在潜能，教师可以从教学实际出发，为学生搭建一个“说数学”的平台.通过“说”让学生表达自己的所思、所想、所惑，充分调动学生参与课堂的积极性，激发学生的主观能动性，让学生在互动交流中学会思考、学会合作，切实提高学生数学学习能力.

关键词：说数学；思考；合作数学课堂不是教师或个别学生的专场秀，而是师生互动交流、共同参与的舞台.在参与和互动中，学生积极表达自己之所思、所想、所惑，从而通过有效地交流让每个学生都能有所获.为了让学生更好地参与课堂，教师应为学生创造一个平等、和谐的学习氛围，结合教学实际设计一些趣味性、探究性的教学情境，引导学生积极思考、主动表达，以此提高课堂教学有效性［1］.不过，因受传统“师讲生听”教学模式的影响，学生对教师产生依赖，学习缺乏主动性、积极性，在面对新问题时不知该如何思考、如何表达.为了改变这一局面，在教学中，教师要预留一些时间让学生“说数学”，让他们把自己的思维和结果清晰地表达出来，由此了解学生的思维漏缺，以便通过有效的启发和引导帮助学生克服困难，提高学生分析和解决问题的能力［2］.

所谓“说数学”就是让学生把对数学问题的一些想法、思路、过程等用口头语言表达出来.对于书面表达，其所呈现的是完整的解题思路，而“说数学”比较广泛，它可以是学生对某个知识点的理解；可以是学生对解题过程的见解；可以是对数学文化所表达出的所思所想；也可以是学习中的一些体会、感悟等等.可见，“说数学”为师生和生生互动交流提供了更为自由，更为广泛的资源，在教学中合理利用将有利于提升学生的综合能力和综合素养.

笔者以“平面向量基本定理”为例，在教学中，教师鼓励学生动口说，通过“说”激发学生的参与热情，让学生体验知识发生和发展的过程，并在参与中深化知识理解，提高教学有效性.

1教学简录1.1回顾旧知，导入新课问题1：我们已经学习了向量的共线定理，谁来说一说，你是如何理解的？

设计意图：教师从学生已有知识、经验出发，精心创设问题，以此借助问题诱发学生思考，吸引学生注意力，提升教学有效性.同时，通过与旧知相联系，为新知探究提供知识储备.

评注：在本课教学前，教师应鼓励学生及时巩固旧知识，预习新内容，以此通过新与旧的碰触产生新问题，这样学生带着问题学习可以有效地提升听课效率.在实际教学中，教师要结合教学实际提出问题，也要鼓励学生发现并提出问题，以此充分发挥问题在引发学生思考，激发学生探究欲等方面的优势，提升教学有效性.在本环节，教师结合教学实际提出问题，在问题的驱动下帮助学生回顾知识点，并通过“说”表达自己的想法和见解，为新知识的学习打下坚实的基础.

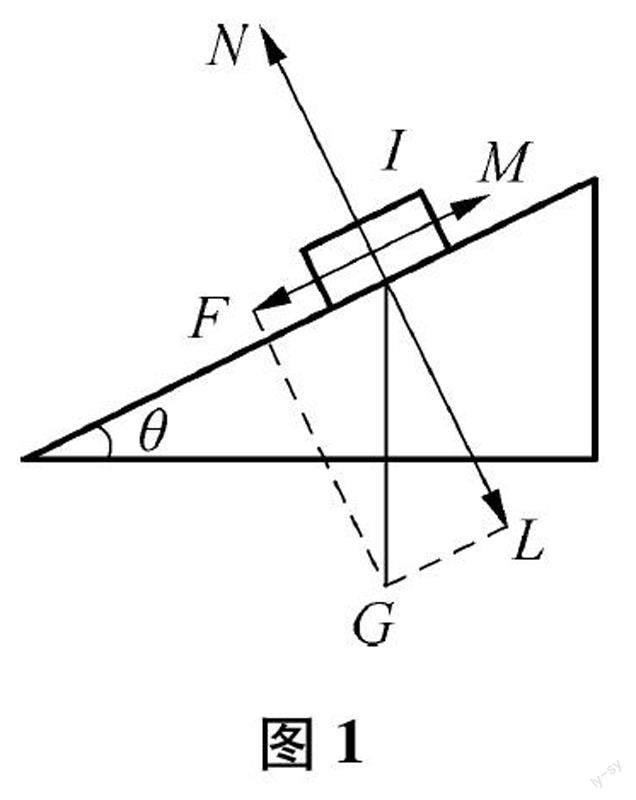
1.2跨科联想，建立模型问题2：结合物理学的知识，请大家思考：对于平面内的任一向量可以如何表示呢？

（1） 如图1，画出静止在斜面上物体所受重力的示意图.

（2） 如图2，画出火箭飞行的速度分解的示意图.

设计意图：从学生熟悉的问题出发，引导学生运用物理学知识进行力和速度的分解.这样通过与其他学科知识相联系，让学生清晰认识这一物理问题的本质与新知探究的内容本质一致，通过上面知识和经验的迁移加速了定理的形成.

评注：在教学过程中，教师先是引导学生通过动手画获得直观感知，然后组织学生动口说，通过互动交流发现问题的本质，激发学生学习的热情，进而为后期自主探究作铺垫［3］.

1.3巧设问题，激活思维问题3：结合向量共线定理的相关内容，请思考：对于确定的、不共线的向量e₁和e₂，“任一向量a”的这种分解是否成立呢？如果成立，在a=λ₁e₁+λ₂e₂中，实数λ₁，λ₂是否唯一？如果不成立，请说明理由.

设计意图：通过前面几个问题的探究，学生对平面向量基本定理及几何意义已经有了初步的了解，知晓平面向量是可以合成和分解的.在已有知识和经验的基础上继续引申，让学生思考如何用其它量来表示.有了前面的铺垫，学生在探索新问题的过程中自然会联想向量共线定理的相关内容，进而主动类比、分析、概括、交流，通过“说数学”逐渐找到解决问题的方法，突破教学难点.

评注：问题3是本课教学的一个难点问题，也是教学的一个重点，学生理解起来比较困难.对于教学重难点内容，大多教师习惯于通过讲授的方式加以呈现，然后借助练习进行强化，这样表面上帮助学生突破了难点，但是因为学生独立思考和合作交流过程的缺失，影响学生能力的发展.因此，在教学中，教师不能直接将结果抛给学生，要提供机会让学生去思考和交流，以此让学生学会思考，学会学习.在这里，为了帮助学生突破重难点，教师应精心创设问题，让学生通过类比讨论找到解决问题的方法，发现问题的結论.

1.4概念辨析，深化理解问题4：结合以下分析说一说，你是如何理解平面向量基本定理的呢？

（1） 对于向量e₁和e₂，要满足什么条件才能作基底呢？

（2） 基底唯一吗？

（3） 定理中的λ₁和λ₂唯一吗？

设计意图：经过以上探求，概念已经形成，不过学生对概念的理解可能缺乏深刻性.在此环节，教师精心设计问题串，让学生在问题的驱动下明晰定理的本质.

评注：概念、定理等内容具有高度的概括性，学生理解起来会比较困难，为此教师要鼓励学生“说”，这样既可以降低思维的难度，提高学生探索的积极性，又可以培养学生思维的严谨性和深刻性，加深学生对概念的理解.在以上问题的探索中，学生难免会遇到障碍，教师要充分发挥其课堂引导者的作用，引导学生通过思考交流明晰概念的本质，促进知识的深化.

1.5例題精析，升华认识例1如图3，已知四边形ABCD为平行四边形，连接AB，BD交于点M，且AB=a，AD=b.用基底a，b表示MA，MB，MC，MD；E，F分别是BC，CD的中点，用基底a，b表示BF，DE.

设计意图：在本环节的教学中，教师可以先让学生独立思考，然后开展小组探究活动，让学生一起“说”，相互揭短，相互补充，集思广益，总结归纳向量的表示方法.以上探索、发现、归纳的过程有助于学生知识的内化，有助于学习能力的提升.

评注：练习是巩固知识，提升技能的必经之路.在例题讲解时，教师切勿直接将教材标准答案呈现给学生，应预留时间让学生思考和交流，以此提升学生学习能力，发展学生数学素养.

2教学思考在传统数学教学中，大多师生习惯于“讲数学”“做数学”，即教师将相关的知识、经验、方法等通过讲授的方式传授给学生，然后通过相应的练习让学生进行知识的巩固和强化，这样学生的“学”是被动的、消极的，不利于学生独立思考能力的提升和合作意识的培养.为了改变这一局面，在教学中，教师可以引导学生“说数学”，让学生充分表达自己的想法和见解，创新性地提出解决问题的方法，以此培养学生的创新意识，发展创新思维.在学生“说”的过程中，教师要做一名合格的倾听者，了解学生所思、所想、所惑，积累教学素材，以便通过有针对性的启发和引导帮助学生找到思考的方向.

学习是一个不断完善和发展的过程，在学习中可能会遇到各种各样的问题，只有让学生掌握探索问题的方法，树立正确的学习观，才能让学生有所发展、有所成长.同时，在学习过程中，教师要鼓励学生合作交流，学会互相学习、共同面对，进而培养学生的合作意识，提高学生的数学核心素养.值得注意的是，在学生互动交流过程中，教师也要参与其中，了解学生的所想、所惑，从而通过有针对性地启发和引导帮助学生找到解决问题的方法，以此培养他们的学习技能，提升数学素养.参考文献：

［1］ 钟进均.基于“说数学”实践的创新思维培养案例探究［J］.数学通讯，2019（7）：1115.

［2］ 宁菊英.善言能解知己知彼——浅谈高中生数学交流能力培养［J］.高考，2021（5）：100101.

［3］ 王眉燕.渗透数学思想方法 培养数学核心素养［J］.数学教学通讯，2017（13）：5556.