A Privacy-Preserving Federated Learning Algorithm for Intelligent Inspection in Pumped Storage Power Station

Yue Zong ,Yuanlin Luo ,Yuechao Wu ,Wenjian Hu ,Hui Luo ,Yao Yu,*

1 Power China Huadong Engineering Corporation Limited,Hangzhou,Zhejiang 311122,China

2 School of Computer Science and Engineering,Northeastern University,Shenyang,Liaoning 110819,China

Abstract: As a distributed machine learning architecture,Federated Learning (FL) can train a global model by exchanging users’model parameters without their local data.However,with the evolution of eavesdropping techniques,attackers can infer information related to users’local data with the intercepted model parameters,resulting in privacy leakage and hindering the application of FL in smart factories.To meet the privacy protection needs of the intelligent inspection task in pumped storage power stations,in this paper we propose a novel privacy-preserving FL algorithm based on multi-key Fully Homomorphic Encryption(FHE),called MFHE-PPFL.Specifically,to reduce communication costs caused by deploying the FHE algorithm,we propose a self-adaptive threshold-based model parameter compression(SATMPC)method.It can reduce the amount of encrypted data with an adaptive thresholds-enabled user selection mechanism that only enables eligible devices to communicate with the FL server.Moreover,to protect model parameter privacy during transmission,we develop a secret sharing-based multi-key RNS-CKKS(SSMR)method that encrypts the device’s uploaded parameter increments and supports decryption in device dropout scenarios.Security analyses and simulation results show that our algorithm can prevent four typical threat models and outperforms the state-of-the-art in communication costs with guaranteed accuracy.

Keywords: federated learning (FL);fully homomorphic encryption (FHE);intelligent inspection;multikey RNS-CKKS;parameter compression

I.INTRODUCTION

With the rapid development of Internet of Things(IoT) technologies,the intelligent construction of the pumped storage power station has become an inevitable trend[1].For example,intelligent inspection technologies based on 5G IoT sensors and inspection robots are applied to replace traditional manual inspection methods[2,3].Such technologies can avoid the uncertainty of manual field operations and improve maintenance efficiency with low labor casts.However,there are still some security problems.On the one hand,in these technologies,the complete inspection data is needed to transmit back from each device to the data center in the power station for training and analysis,so the real-time identification and alarm of the abnormalities in devices and environment cannot be guaranteed.On the other hand,attackers can easily intercept the inspection data during transmission,thus causing leakage of sensitive information and undermining power station security.

To solve the above problems,in this paper we consider a Federated Learning (FL) architecture that allows devices to train data locally and protects the privacy of intelligent inspection data collected by smart devices.FL is a distributed machine learning architecture that protects participants’local data privacy by sharing the updated model parameters instead of local data during the training process,and can also achieve the purpose of training the global model[4].However,there is still the risk of indirect privacy leakage in FL architecture.Attackers can obtain private information of local data by backward inference based on the intercepted model parameters[5,6].

In summary,various IoT terminal devices in the power station can autonomously analyze their safe operation status and diagnose fault problems when the FL architecture is enabled,but its privacy protection capability needs further improvement.To this end,in this paper we propose a novel privacypreserving FL algorithm based on multi-key Fully Homomorphic Encryption (FHE),called MFHE-PPFL,to meet the privacy protection needs of the intelligent inspection task in pumped storage power stations.The MFHE-PPFL algorithm consists of two parts: a self-adaptive threshold-based model parameter compression (SATMPC) method for parameter compression and a secret sharing-based multi-key RNS-CKKS(SSMR) method for encryption and decryption.Our contributions can be organized as follows.

· To reduce the computation and communication costs while enhancing privacy protection by FHE,we propose the SATMPC method that utilizes an adaptive thresholds-enabled user selection mechanism to control that only eligible devices can communicate with the FL server.

· To enhance the protection of uploaded model parameters,we propose the SSMR method,which encrypts the model parameters uploaded by devices and can also prevent decryption failure due to some of the devices dropping out.

· By conducting exhaustive security analysis and experimental simulations,our proposed MFHEPPFL algorithm can prevent four typical threat models and outperform the state-of-the-art in communication costs with guaranteed accuracy.

The remainder of this paper is organized as follows.Section II introduces the related works of existing privacy-preserving FL algorithms.Section III illustrates our system model and four typical threat models.Section IV presents the details of our proposed MFHE-PPFL algorithm.Security analysis and simulation results are shown in Section V and Section VI,respectively.Section VII concludes this paper and provides future work.

II.RELATED WORKS

Recently,a multitude of methods has been proposed to address FL privacy leakage problems.Zhuetal.[6]studied the attack methods to infer participants’ sensitive information based on model parameters shared in FL.To enhance the privacy protection of these shared parameters,some works resort to cryptographic methods to protect data during transmission in the FL framework,such as differential privacy (DP),secure multi-party computation (SMPC),and homomorphic encryption(HE).

Xuetal.[7]enhance the FL privacy protection capacity by employing DP and SMPC based on multiinput function encryption(MIFE).Aonoetal.[8]proposed an additive HE method to encrypt the gradient uploaded by each user,and the FL server aggregates the ciphertext before decrypting it,which can avoid the privacy leakage of user data.Savetal.[9] developed a method to encrypt user data during the complete FL process to achieve that the information shared between users and the FL server is always ciphertext during the training period.However,the method in[9]adds significant computation overhead to each client,which reduces the local training efficiency and increases the communication overhead between the FL server and clients.Yinetal.[10]proposed a privacypreserving FL algorithm based on function encryption and Bayesian differential privacy mechanism,which uses the method of sparse differential gradients to improve the transmission efficiency.

In addition,Maetal.[11] proposed a privacypreserving FL algorithm based on XMK-CKKS,which guarantees the confidentiality of model updates by encrypting them with multi-key homomorphic encryption.However,for an aggregated ciphertext,the algorithm in [11] requires cooperative decryption by all participating devices,which is inflexible.

The above works adopt some privacy-preserving methods to protect the model parameters shared by users and the FL server during the training process.In particular,encryption technologies have a good privacy protection effect,where the FHE method can meet the needs of multiple types of arithmetic and is more suitable for use in FL environments than the traditional HE method.Although a few works have enabled FHE in the FL architecture,the high computation and communication costs caused by the deployment of FHE have not been addressed,especially in the intelligent inspection system of pumped storage power stations.

III.SYSTEM MODEL

3.1 Privacy-Preserving FL Model

To protect the inspection data privacy,we propose a privacy-preserving FL model for the pumped storage power station’s intelligent inspection system,as shown in Figure 1.The model framework comprises three elements: the device layer,server layer,and a thirdparty authority(TPA).

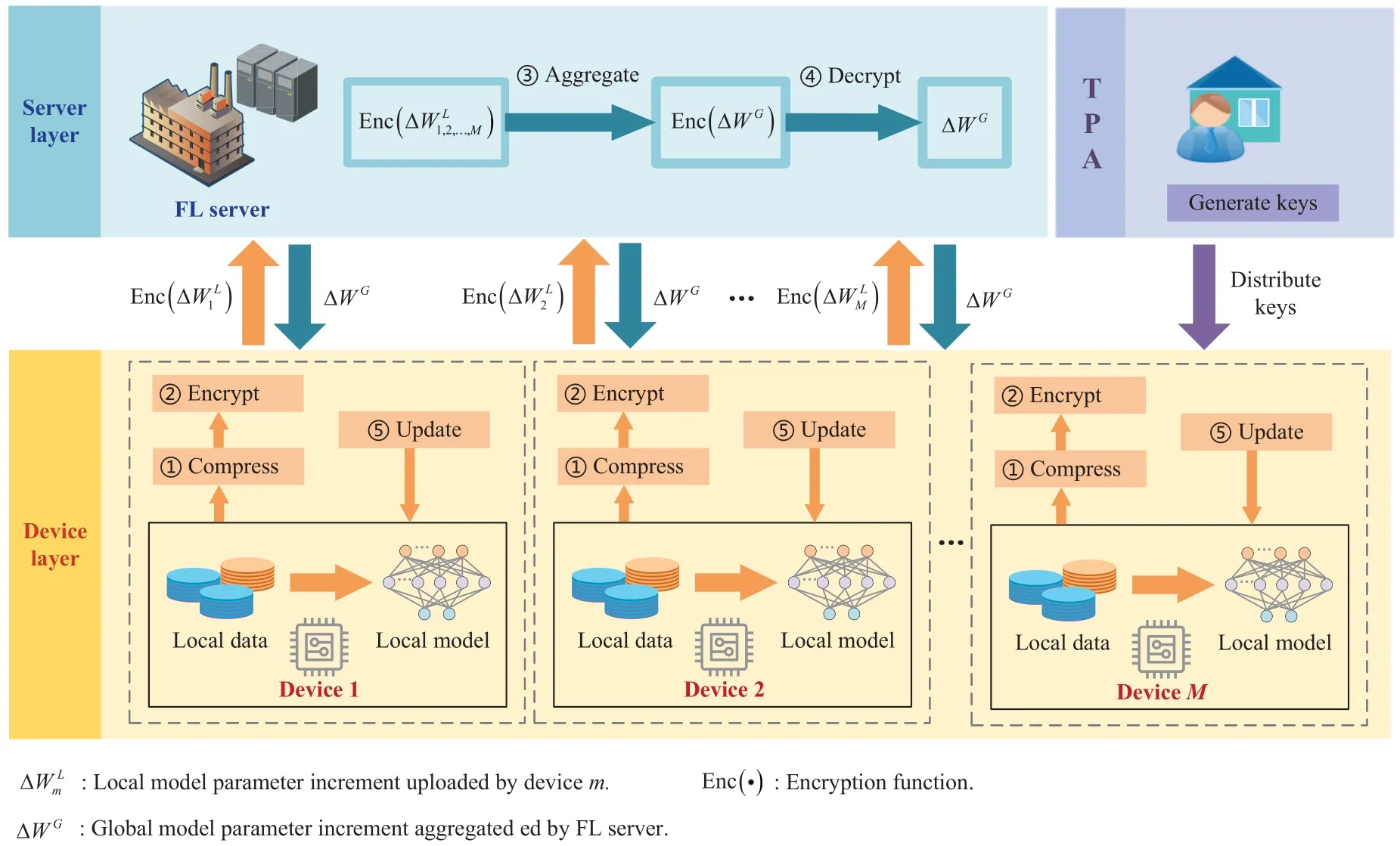
Figure 1.Privacy-preserving FL-based system model.

Device layer.The device layer consists of all intelligent inspection devices participating in FL.Each of them independently collects inspection data and trains its own model locally.

Server layer.The server layer contains an FL server.It can communicate with each device to collect its local model parameters,and then aggregates these parameters to train the global model.Eventually,it returns the global model parameters to the devices.As such,without exchanging inspection data,each device can build a global model by exchanging only its local model parameters.

TPA.The TPA generates each device’s public and private keys and distributes them via a trusted channel.Each device can encrypt the local model parameters that need to be uploaded to the FL server with its own keys and assist the FL server in decrypting the aggregated ciphertext.

Note that in our scheme,to reduce the risk of local model parameter leakage,we choose to upload the local model parameter increment in two adjacent FL training rounds to the FL server.Our simulation results in Section IV demonstrate that this approach can ensure the FL training proceeds properly with guaranteed accuracy.The training process can be organized as follows.

In an FL training round,each device first trains its local model with its collected inspection data and compresses the model parameter to obtain the increment that meets the upload conditions in our SATMPC method.Then,the local model parameter increment is encrypted and uploaded to the FL server.Next,the server aggregates all received ciphertexts of devices’local model parameters via homomorphic operations to obtain the ciphertext of the global model parameter increment.It is further decrypted with the collaboration of multiple devices.Finally,the global model parameter increment is transmitted back to all devices.,and each device uses it to update the local model.Such a loop will continue until the FL training objective is reached.

3.2 Threat Model

There are four typical security threats in the FL-based intelligent inspection system of the pumped storage power station.

· The devices are honest but curious,which means that they follow the protocols during training but are curious about the private information of other devices.

· The devices may collude with the server or each other to infer the private information of a specific device.

· An external attacker may infer information related to the device by eavesdropping on the information transmitted between the server and the device during training without interrupting the transmission of information or inserting harmful information.

In the following,we provide a detailed description of the potential inference attack in the above security threats according to [6].The training process of the device’s local model can be expressed asy=F(x,W),wherexis the input local data,Wis the local model parameters,andyis the output result.We can optimizeWby the loss function to keepyclose to the label.Note that the device’s local model architectureF() is shared by default for most FL applications.We assume that an attacker gets a device’sWand performs an inference attack on its local data.The attacker can be another device,a server,or an external attacker.First,the attacker initializes a set of dummy datax′and its corresponding dummy labely′,and inputsx′toF()for training to obtain the trained model parametersW′.Then,the attacker calculates the gradient distance betweenWandW′,and dynamically adjustsx′andy′according to the gradient distance for repeated training to makeW′approximateW.In this process,x′andy′also keep approximatingxandy.When the gradient distance is minimized,the attacker’s dummy datax′*and dummy labely′*will also converge to the attacked device’s local data and labels,which can be expressed as (1).Therefore,the attacker can infer the device’s local data in the above way,resulting in privacy leakage.

IV.MFHE-PPFL ALGORITHM

Unlike traditional open FL algorithms,our proposed MFHE-PPFL algorithm protects device data privacy by two crucial operations:parameter compression and encryption.The design details are as follows.

4.1 Parameter Compression

Since FHE makes the FL-enabled inspection system bear high computation and communication costs,according to[12,13],we propose the SATMPC method to solve the above problem by reducing the amount of encrypted data that needs to be uploaded.Specifically,our SATMPC method contains two critical operations.First,in each global iteration,all participating devices in the FL calculate their local model parameter increments after the local models are trained and then obtain the threshold value according to the previous global model parameters and their sample proportion.Second,each device compares its parameter increment with the threshold value,and the devices whose parameter increment is larger than the threshold value are selected to transmit the encrypted parameter increments to the server.By doing so,we can reduce the FL computation and communication overhead caused by the excessive amount of uploaded parameters with guaranteed global model accuracy.

After that,the server aggregates the received parameter increments and sends the aggregated values to each device that adds the received value to its previous round’s global parameter to obtain the current round’s global parameter.Note that the device can communicate with the server only if it has a parameter increment that reaches the threshold value;otherwise,the increment is accumulated locally until the threshold value is reached.Moreover,the threshold value is adaptively adjusted according to the changes in all device parameters in each round.The solution process of our self-adaptive threshold value is as follows.

He looked around the lake. No other fishermen or boats were anywhere around in the moonlight. He looked again at his father. Even though no one had seen them, nor could anyone ever know what time he caught the fish, the boy could tell by the clarity of his father’s voice that the decision was not negotiable. He slowly worked the hook out of the lip of the huge bass and lowered it into the black water. The creature swished its powerful body and disappeared. The boy suspected that he would never again see such a great fish.

We assume that the participants in FL consist ofMdevices and a server,whereMdevices constitute the setM={1,2,...,M}.Mcan be divided into a setMLof lazy devices and a setMHof hardworking devices,where lazy devices refer to devices that do not communicate with the server in each global iteration (i.e.,devices that can be ignored),hardworking devices refer to devices that communicate with the server in each global iteration,and the size ofMcan be calculated by|M|=|ML|+|MH|.Then,we assume that in thet-th iteration,the global model parameter sent by the server to all devices isW(t),the local model parameter updated by devicemis,and the global model parameter updated by the server isW(t+1).The number of samples for devicemisNm,and the total numberNof samples for all devices can be calculated byN.As such,the global model parameter increment in thet-th global iteration can be calculated by

Through the numerical relations,we can obtain that the increment ofMLupdated locally satisfies

Since the size ofMLis unpredictable,we let|ML|=β|M|.Moreover,ΔW(t+1)=W(t+1)-W(t) is only available at the next iteration,so we use the increment of the previousDrounds to estimate the increment of the current round,as follows.

whereξdis a weight.Therefore,we can obtain

In summary,when the device’s local model parameter increment satisfies (6),it can be judged that this device belongs toMLand does not communicate with the server in the current global update round.Devicem’s threshold valueηmcan be expressed as

4.2 Encryption and Decryption

Traditional FHE only supports integer operations,while the model parameters are floating-point in FL with multi-device participation.When applying traditional FHE to FL,we need to quantify floating-point numbers to integers and encrypt them,which will reduce the model’s accuracy.In addition,the single-key encryption approach increases the risk of device privacy leakage in FL.Once a device’s private key is compromised,the ciphertext of other devices can be decrypted.

To solve the above problems,we propose a novel FHE algorithm for FL privacy protection according to [14–17],namely a secret sharing-based multi-key RNS-CKKS (SSMR) method.It supports floatingpoint arithmetic and only requires partial devices participating to decrypt,avoiding the situation where devices drop out the FL after uploading parameters resulting in the aggregated ciphertext cannot decrypt.The specific process is as follows.

Step 1: SetupSetup（q,L,η,1λ）.In this step,a base integerq,the number of levelsL,and the bit precisionηare given as the inputs with the security parameterλ.We denote the ring of cyclotomic polynomials defined for the plaintext space asR=,whereNRis a ring dimension that is a power of two.With the fixed base integerq,a ciphertext modulus at the levelLis typically defined asQ=p0qL.The residue ring defined for the ciphertext space can be expressed asRQ=R/(Q·R)=.The RNS basis consisting of approximate values of the fixed baseqis denoted asB={q0,q1,...,qL},whereqiis a prime number.As such,the ciphertext modulusQat the levelLis computed asQ=and the ciphertext space isRQ=.Set the small distributionsχs,χe,andχroverRfor secret,error,and encryption,respectively.The random sampling is denoted asa←RQ,and its RNS is denoted as[a]B=(a(0),a(1),......a(L)).Return the common parameter pp=(NR,Q,χs,χe,χr,[a]B).

Step 2: Key generationKeyGen(pp).Generate the main private key sk=(1,s),wheres←χs.The corresponding public key can be expressed as

whereb(j)=-a(j)·s+e(modqj)ande←χe.Assign a private key share(xi,si)to each device through the secret sharing protocol,and each device’s private key can be expressed as ski=(1,si),1≤i≤M.

Step 3: EncodingEcd(z,Δ).Encode anNR/2-dimensional complex (real) vectorz∈into a polynomial Mtext(X)=σ－1（R,where Δ is a scaling factor,π－1()denotes the expansion of the message vector fromandσ－1() denotes the inverse of canonical embedding.

Step 4: EncryptionEnc(mi,pk).Deviceirandomly samplesri←χrandei0,ei1←χe,so the plaintext miis encrypted as

At this point,the devices selected by our SATMPC method have encrypted their model parameter increments locally.Next,they upload these ciphertexts to the server for aggregation.The specific aggregation process is shown in steps 5-7.

Step 5: Multiplying the weights with the ciphertextCmult（The aggregation process on the FL server is equivalent to the process of weighted summation over all elements.In this step,the weight of the ciphertext Ciuploaded by device i is.The operation of multiplying it with the ciphertext can be expressed as

Step 6: RescalingRescale(MCi,Δ).The multiplication of ciphertext and scalar will reduce the precision of decryption result.To compensate for the loss of precision,we perform the rescaling operation on MCito obtain the processed ciphertext RMCi.The rescaling operation can be expressed as

Step 7: Additive homomorphismAdd(RMC1,RMC2,...,RMCn).Assuming that the server receives the ciphertexts fromndevices,and the aggregated ciphertext Csum can be expressed as

Step 8:DecryptionDec(Csum,si).Randomly selecttonline devices denoted as setU,wheretsatisfies the constraint on the number of participants in the secret sharing protocol[18].Each device inUcomputes its decryption share Dias

where msumis the decryption result.

Step 9: DecodingDcd(msum,Δ).Convert polynomial msumto complex vector using the inverse process of encoding to obtain the aggregated global model parameter increment.

In general,the process of our multi-key encryption and decryption can be organized according to three distinct phases.First,each device encrypts its parameter increments by the same public key and uploads the ciphertext to the server for aggregation.Second,the server returns the aggregated ciphertext to the participating devices for decryption.Each participating device decrypts the ciphertext by its unique private key to obtain a decryption share and uploads it to the server.Finally,the server aggregates all the decrypted shares to obtain the decryption result and returns it to each device.By doing so,no single device can decrypt all ciphertexts independently but requires the other devices to permit and cooperate.

Following the above design,we develop the MFHEPPFL algorithm by combining our proposed SATMPC method and SSMR method with FL architecture,as shown in Algorithm 1.

V.SECURITY ANALYSIS

This section analyzes the security of our proposed MFHE-PPFL algorithm for the four common threat models introduced in Section III.Specifically,the MFHE-PPFL algorithm has the following four security features.

Prevent the honest but curious server from accessing sensitive information related to device data.On the one hand,the data shared between the device and the server is the increments of local model parameters rather than the complete parameters.The attacker cannot recover the device’s private data by the gradient matching algorithm.On the other hand,with the encryption method SSMR,the server can only obtain the ciphertext of the device’s local model parameter increments and the aggregation result,which guarantees the privacy of the device data.

Avoid honest but curious devices gaining access to other devices’private information.Since SSMR is a multi-key encryption method,devices need to decrypt the ciphertext through collaboration.As such,honest but curious devices cannot reason out other devices’private information by obtaining the shared information.

Resist collusion attacks from devices or with servers.We give theorems and proofs for two cases as follows.

Theorem 1.Inthecaseofcollusionattacksinvolvingusersandtheserver,whenthenumberofcollusion devicesislessthantheminimumnumberofdevices requiredfordecryption,otherdevices’parameterinformationissecure.

Proof.The minimum number of devices required for decryption is denoted asMs,and we assume that there areMs-1 devices who conspire with the server to try to obtain the plaintext informationmiof honest devicediby computingand merging it withThe merging process is as follows.

whereUcdenotes the collusion device set.Since the number of collusion devices isMs-1,sj(modq)/=mi.As such,even ifMs-1 devices conspire with the server,they cannot decrypt the ciphertext of honest devicedi,which can guarantee device data privacy and security.

Theorem 2.Inthecaseofcollusionattacksinvolvingonlydevices,whenthenumberofcollusiondevices islessthantheminimumnumberofdevicesrequired fordecryption,otherdevices’parameterinformation issecure.

Proof.Collusion devices may infer from the decrypted aggregation resultHowever,since the number of collusion devices does not exceedMs-1(Ms＜|M|)and the components of the aggregation result satisfy

whereUhdenotes the honest device set,the attacker can only obtain the sum of local model parameter increments of|M|-Ms+1 honest devices through the aggregation result and cannot obtain a particular device’s parameter increment.Therefore,the collusion attack is unsuccessful in this case.

Prevent external adversaries from gaining access to sensitive information related to devices’ private data.External adversaries can only obtain the ciphertexts of the shared parameter increments by listening and cannot infer devices’ private data with them,which guarantees that any adversary monitoring the communication channel during the training period cannot reason about devices’private data.

VI.SIMULATION RESULTS

In this section,we evaluate the performance of our proposed MFHE-PPFL algorithm in model test accuracy and communication cost through extensive simulations.Our MFHE-PPFL is implemented using Pytorch,a fast and flexible machine learning framework.For the software environment,we utilize Py-Torch 0.4.0 with Python 3.6 and its FHE library in a Windows 10 system.The detailed simulation settings and results are presented as follows.

6.1 Simulation Setting

To make our proposed MFHE-PPFL algorithm have good stability and fast convergence ability,the parameter settings used in the simulations are summarized in Table 1.We use the available MNIST dataset to approximate the inspection dataset in the pumped storage station.The local model of each device is a three-layer MLP model with the optimization algorithm SGD,and the number of neurons in the input layer,two hidden layers,and output layer is 784,200,200,and 10,respectively.ReLU is used as the activation function for the hidden layers.

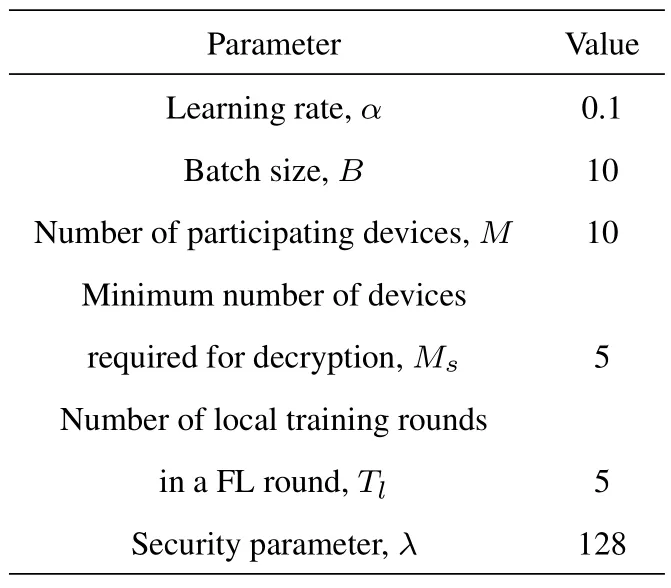
Table 1.Simulation parameter settings.

6.2 SATMPC Method Performance

· Setting of ξd and β

We assume that the global model parameter increment in the current round can be represented by that of the previous round.Based on this,we letD=1 in (4) and get ΔW(t+1)=ξdΔW(t),whereξdis the weight that varies with the number of global communication roundsx,which can be calculated by linear regression as

In our proposed MFHE-PPFL algorithm,βaffects the parameter compression degree and the model’s accuracy.The former can be measured by the compression ratio,which is defined by

whereNaandNbrespectively denote the number of communications after and before compression.It is clearly seen that the smaller the compression ratio,the greater the compression degree.Note that as the compression ratio gradually decreases,the accuracy of the device’s local model reduces accordingly.

Table 2 shows the influence of differentβon the compression ratio and model accuracy.We find that the model accuracy varies little in theβrange from 0.1 to 1.Therefore,to save the communication overhead,we setβ=0.1 with the minimum compression rate to reduce the number of communications between the device layer and the server layer as much as possible.

Table 2.Compression rate and accuracy rate with different β.

· Effectiveness Analysis

To verify the effectiveness of our proposed SATMPC method,we compare our SATMPC-enabled MFHE-PPFL algorithm with the non-SATMPCenabled MFHE-PPFL algorithm in model test accuracy and communication cost,as shown in Figure 2 and Figure 3.

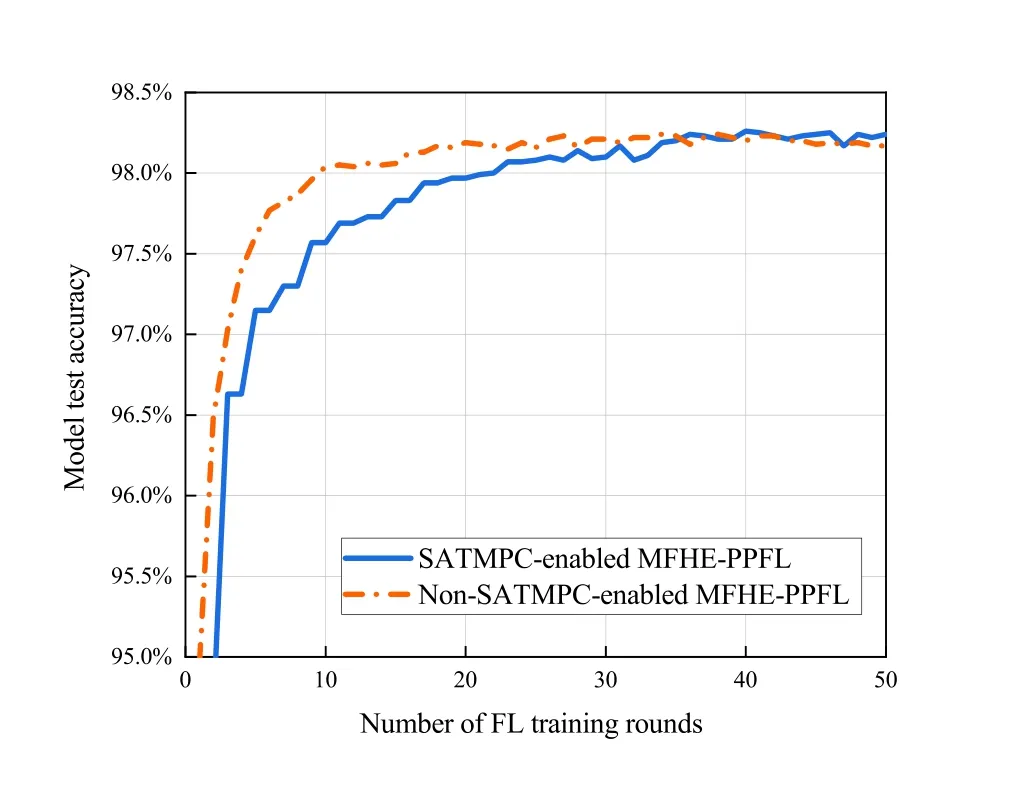
Figure 2.Model test accuracy comparison of MFHE-PPFL with and without SATMPC enabled.

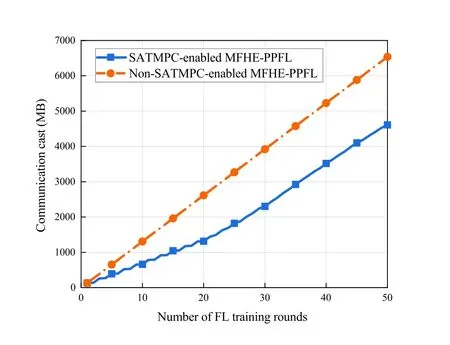
Figure 3.Communication cost comparison of MFHEPPFL with and without SATMPC enabled.

We can see from Figure 2 that although the convergence speed is decreased,the model test accuracy after the convergence of both algorithms is almost the same.It illustrates that enabling our SATMPC method does not affect the final accuracy and performance of the model.The advantage of enabling the SATMPC method in communication cost is shown in Figure 3.Note that we use the cumulative communication data size at the current FL training round to measure the cumulative communication cost in the FL process (communication cost for short) because they are proportional.After convergence,the accuracy of SATMPC-enabled MFHE-PPFL and non-SATMPC-enabled MFHE-PPFL respectively reaches 98.23% and 98.21%,and the communication cost of devices is 2923.18MB and 3790.77MB.This is because after parameter compression,in each FL training round,only devices with large changes in local model parameters upload their parameter increments to the server,not all devices.Therefore,our SATMPC method can reduce the communication cost between the device layer and server layer in the pumped storage power station’s intelligent inspection system without affecting the model performance.

6.3 MFHE-PPFL Algorithm Performance

We verify the performance of our proposed MFHEPPLF algorithm in terms of model testing accuracy and communication cost,which is measured by the communication data size.Besides,we demonstrate that our algorithm can still help the server decrypt the model parameter increment even when some of the devices drop out.The benchmark for comparison is chosen as the privacy-preserving FL algorithm based on XMK-CKKS in[10],called XC-PPFL.It also adopts the multi-key FHE to protect devices’data privacy,but all devices in it need to upload complete model parameters without parameter compression.

· Comparison of Model Test Accuracy

Figure 4 shows the model test accuracy in different algorithms versus FL training rounds.We can see that our MFHE-PPFL converges from the 35th round with the accuracy of 98.23%,and XC-PPFL converges from the 30th round with the accuracy of 98.22%.Although more rounds are required for our MFHE-PPFL to converge,the final convergence accuracy of both algorithms is almost the same.This can illustrate that parameter compression and uploading of local model parameter increments in our MFHE-PPFL have almost no effect on the model’s accuracy after convergence.

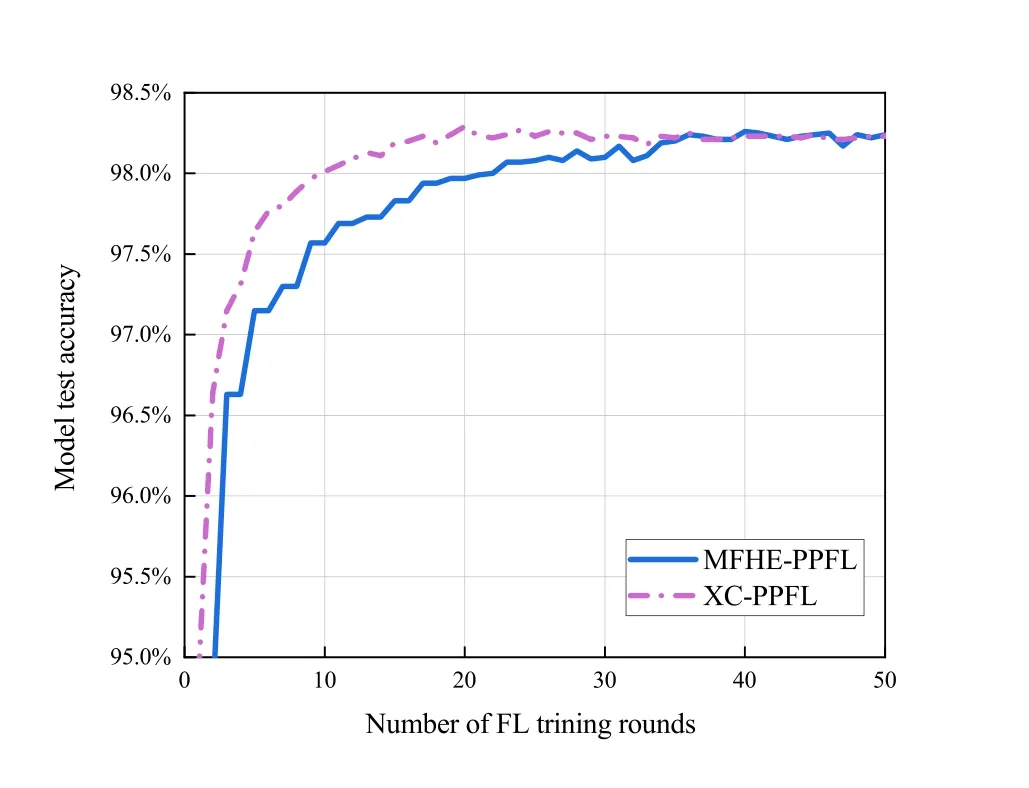
Figure 4.Model test accuracy in different algorithms versus the number of FL training rounds.

· Comparison of Communication Cost

In Figure 5,we count the costs incurred by the devices communicating with the server over the 50 FL training rounds.It can be found that the communication cost of our MFHE-PPFL is much lower than that of XC-PPFL,and our advantage becomes more obvious as the number of FL training rounds increases.Compared with XC-PPFL,our MFHE-PPFL only requires devices with large changes in local model parameters to upload their parameter increments to the server,avoiding the stress and cost caused by all devices uploading complete parameters to the system communication.Moreover,the ciphertext computing process on the server consumes massive computing resources,and our MFHE-PPFL reduces the amount of computing on the server,thus saving computing costs.

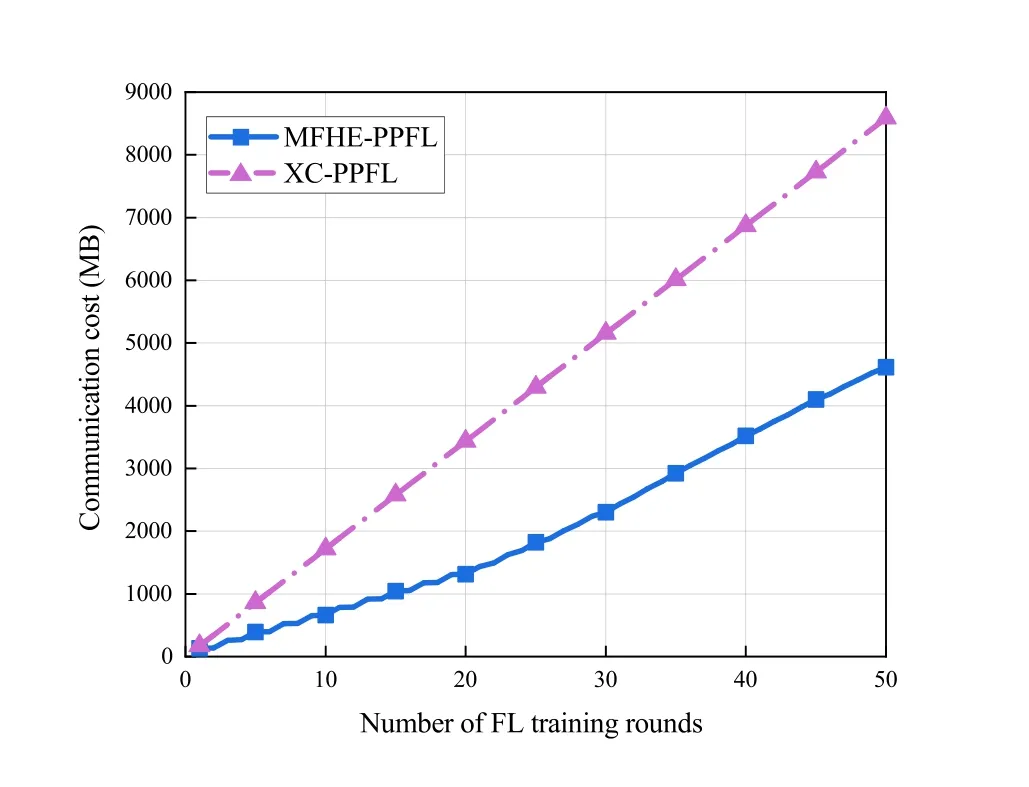
Figure 5.Communication cost in different algorithms versus the number of FL training rounds.

· Device Dropout Case Analysis

Device dropout during the FL training is a common failure in pumped storage power stations.For example,there are two typical scenarios.Scenario I: Due to the vast area of pumped storage power stations,some mobility inspection devices may leave the server’s transmission range and lose connection with the server.Scenario II: Since most pumped storage power stations are built in remote mountainous areas,the network signal of inspection devices is unstable,and the real-time connection with the server cannot be guaranteed.

To verify the robustness of our MFHE-PPFL against device dropout,that is,the remaining devices can still maintain the system performance when some devices are exited,we compare the model accuracy of our MFHE-PPFL and XC-PPFL changes before and after some of the devices drop out.Moreover,we consider 10 devices participating in 50 rounds of FL training,with 1 device dropping out after uploading the parameters to the server in round 10.

From Figure 6,we can clearly see that the device dropout causes a little loss of model accuracy in our MFHE-PPFL,while the model accuracy in XC-PPFL falls off a cliff.This is because in our MFHE-PPFL,devices assist the server in decrypting the global parameter incremental ciphertext by the secret sharing technology,which only requires some of the devices to provide their keys in the decryption instead of all devices.In contrast,XC-PPFL requires all devices to participate in decryption.Once a device drops out,the model training stalls.

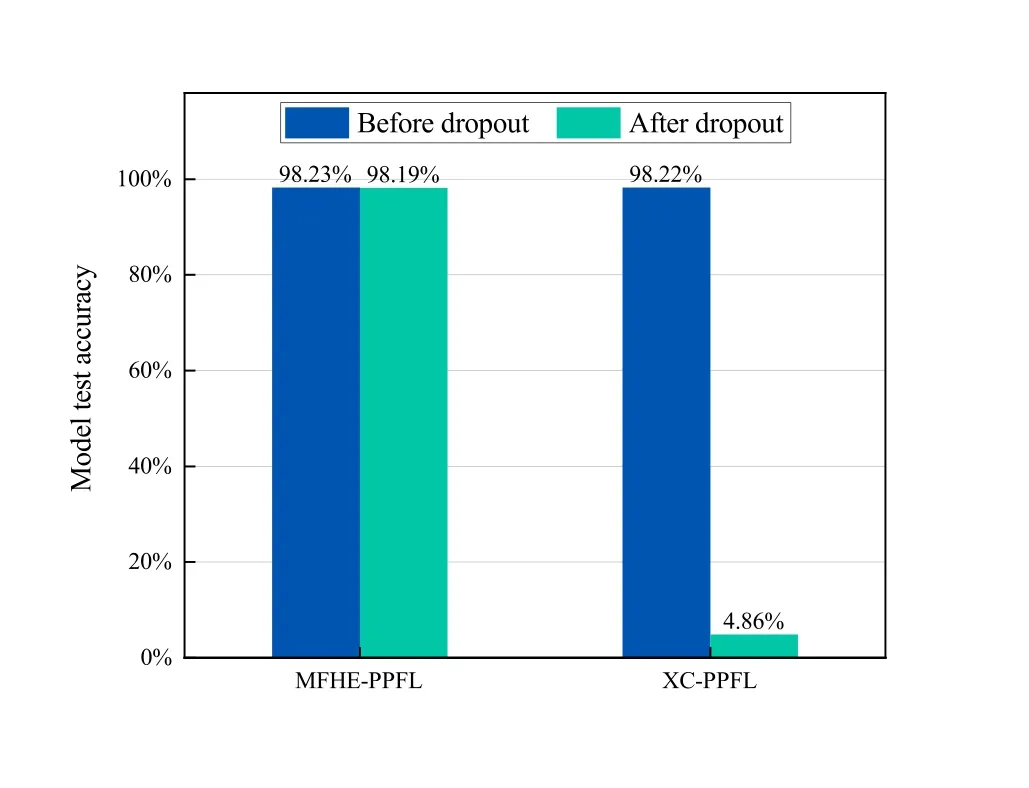
Figure 6.Model test accuracy changes for different algorithms in the device dropout scenario.

Furthermore,Figure 7 shows the variation of the converged model test accuracy in our MFHE-PPFL with the number of dropout devices.As the number of dropped devices increases,the number of training samples available to the global model decreases,thus resulting in reduced model testing accuracy.Nevertheless,even if some of the devices drop out,our MFHEPPFL can still decrypt normally and maintain system performance,which proves its robustness.

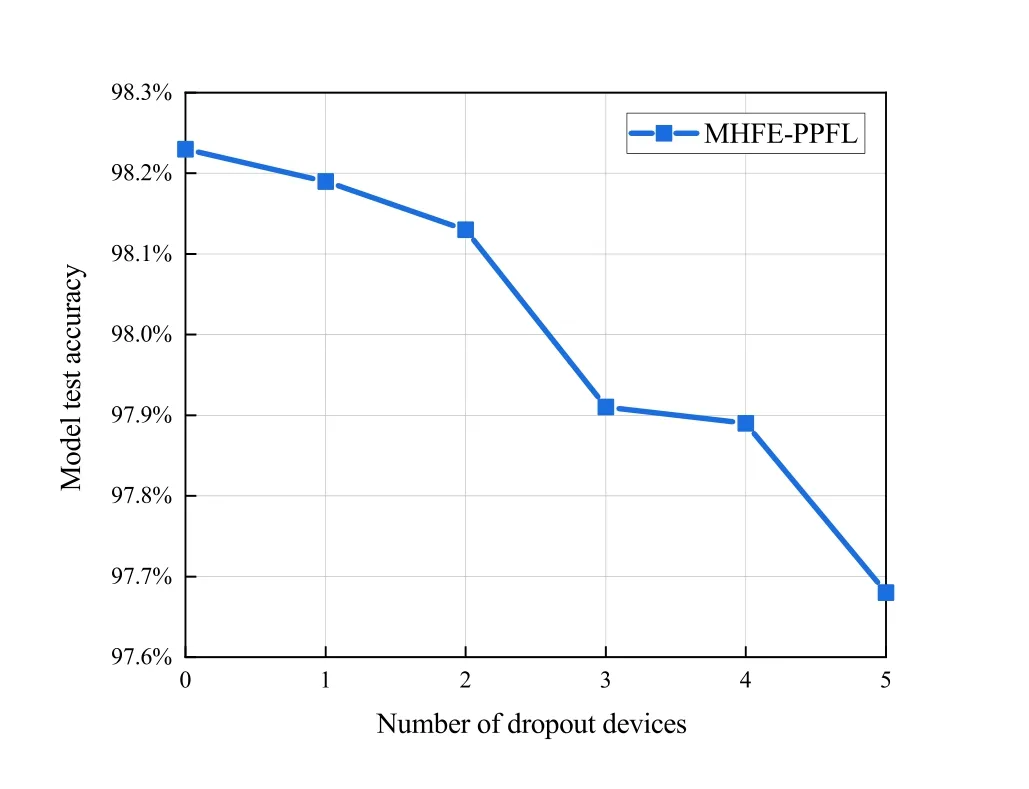
Figure 7.Model test accuracy in our MFHE-PPFL algorithm versus the number of dropout devices.

VII.CONCLUSION

In this paper,we have addressed the privacy leakage problem of FL applied in the pumped storage power station’s intelligent inspection system by our proposed MFHE-PPFL algorithm.In the MFHE-PPFL algorithm,we propose the SATMPC method to reduce the computation and communication costs caused by the FHE deployment through adaptive threshold-based parameter compression.Based on this,we further developed the SSMR method to encrypt and decrypt the parameter increments uploaded by the devices to ensure transmission security.Security analysis and simulation results demonstrate that our MFHE-PPFL algorithm can effectively prevent four typical threat models and reduce the communication cost with guaranteed accuracy.In addition,our algorithm has been proved suitable for device dropout scenarios.Future work is in progress to consider this algorithm in more complex real-world environments with the pumped storage power station.

ACKNOWLEDGEMENT

This work was supported by the National Natural Science Foundation of China under Grant 62171113.