Multi-Objective Optimization for NOMA-Based Mobile Edge Computing Offloading by Maximizing System Utility

Hong Qin ,Haitao Du ,Huahua Wang,* ,Li Su ,Yunfeng Peng

1 Chongqing University of Post and Telecom,Chongqing 400065,China

2 China Mobile Research Institute,Beijing 100000,China

3 School of Computer and Communication Engineering,University of Science and Technology Beijing,Beijing 100083,China

Abstract: Mobile Edge Computing(MEC)is a technology for the fifth-generation(5G)wireless communications to enable User Equipment (UE) to offload tasks to servers deployed at the edge of network.However,taking both delay and energy consumption into consideration in the 5G MEC system is usually complex and contradictory.Non-orthogonal multiple access(NOMA)enable more UEs to offload their computing tasks to MEC servers using the same spectrum resources to enhance the spectrum efficiency for 5G,which makes the problem even more complex in the NOMA-MEC system.In this work,a system utility maximization model is present to NOMA-MEC system,and two optimization algorithms based on Newton method and greedy algorithm respectively are proposed to jointly optimize the computing resource allocation,SIC order,transmission time slot allocation,which can easily achieve a better trade-off between the delay and energy consumption.The simulation results prove that the proposed method is effective for NOMA-MEC systems.

Keywords: computation offloading;mobile edge computing;non-orthogonal multiple access;resource allocation

I.INTRODUCTION

Mobile Edge Computing (MEC) is proposed to support computing-intensive and latency-sensitive applications,such as face recognition,and virtual reality,running on a simple battery-powered User Equipment (UE),by offloading the UE’s computing tasks to the nearby computing servers deployed at network edge[1,2].As a promising high spectrum-efficiency technology for 5G,Non-Orthogonal Multiple Access(NOMA) can accommodate more UEs than the Orthogonal Multiple Access (OMA) by allowing these UEs to work on the same spectrum at the same time[3–12].The Successive Interference Cancellation(SIC)decoding is utilized at the receiver to cancel the co-channel interference among NOMA UEs in order of one by one.

However,due to covering the UE side,MEC serverside,and the intermedia wiressless network,the delay and energy consumption is usually complex and contradictory in the MEC system.NOMA will make the problem even more complex in the NOMA-MEC system.For simplicity,most of the offloading solutions for NOMA-MEC system are single-objective optimization,e.g.,either on energy-optimization [4] or on delay-optimization[5,6].

Among the existing energy-delay joint optimization solutions,Lyu et.al [7] proposed a utility function to combine delay and energy so to translate the multiobjective optimization problem to be one-objective optimization in OMA-MEC system,which is an ingenious design.Using the utility function,Zhang et.al[8] further formulated the delay and energy multiobjective optimization problem for OFDM-MEC system.Using the delay-energy combing utility function,Tran et.al [9] formulated the Quality of Experience(QoE) of users to their mixed integer nonlinear program(MINLP)model of joint task offloading and resource allocation for multi-server MEC networks.Using the same utility function,Zhan et al [10] quantified delay-energy to formulate mobility-aware multiuser offloading optimization for MEC.To cope with the limited energy at devices,Liu et al [13] investigate a joint task generation and computation offloading scheme under a given energy budget for minimizing the age of obtained status updates.The age minimization problem is modeled as a constrained Markov decision process (CMDP).Nouri et.al [14] studied the long-term dynamic tradoff between power and latency in multi-user uplink NOMA-MEC scheme.A stochastic optimization model was present and Lyapunov method was used to solve the problem.Zhu et.al [15] classified the multi-users into pairs and investigated the energy consumption and delay tradeoff in the hybrid NOMA-MEC scheme.However,the limited computing source in the servers at edge is ignored in[14,15].To cancel the mixed internal interference,Jia et.al [16] proposed an iterative and successive interference cancellation (ISIC) approach,and she investigates improve spectrum utilization and cooperative non-orthogonal multiple access scheme that is based on spectrum sensing(CNOMA-SS)in[17,18].

The above solutions using the utility function or weighting function method are for OMA-MEC or NOMA-MEC system.However,the SIC decoding order is fixed according to the order of predetermined channel parameters.In this work,we formulate the multi-objective optimization problems a 0-1 mixed-integer programming problemas in the NOMAMEC system and jointly optimize the computing resource allocation,SIC order,transmission time allocation.We decouple optimization problem into two sub-optimal problems,i.e.a computational resource allocation sub-problem and an offloading decision sub-problem,and then algorithms based on Newton method and greedy algorithm are present.The simulation results prove that the proposed method is effective for NOMA-MEC systems.

II.SYSTEM MODEL AND PROBLEM FORMULATION

We consider a multiuser NOMA-MEC system which consists of N single-antenna UEs U={1,2,...,N},and a single-antenna wireless access point (AP).We assume that each user has only one taskAk≜(Sk,Ck),whereS kkis the total number of bits for the task Ak,and Ckis the number of CPU cycles for 1-bit offloaded data,thus the number of CPU cycles needed for the task is SkCk.The binary offloading model is considered,and the computation offloading decision variable isdk∈{0,1}.Whendk=0,the task is executed locally,and whendk=1 the task is executed at the MEC server.We use NOMA with constant channel conditions.

2.1 Communication Model

The NOMA UEs offload tasks to the AP using same uplink channels.The receiver at the AP decodes users’tasks using SIC method.We let the permutationπover U be the SIC order.The AP decode userπ(N),userπ(N-1),...,π(1).Lethkbe the channel gain from user k to the AP,and pkbe the transmit power of user k.An independent Rayleigh fading channel model is used with channel bandwidth being B and the power spectral density of the complex white Gaussian noise beingN0/2.The transmission rate of k -th decoded userRπ(k)can be expressed as

Proposition 1.Ifallusershavethesametransmission timeconstraintTtand.Theminimum transmissionpowerofk-thdecodeduserpx(k)canbe modeledas

Proof.see appendix A.

2.2 Edge Computing Model

The execution time of edge computing covers the task transmission time and task processing time at the edge server.The computing resource allocated to user k is Fkmeasured in CPU cycles per second and the task processing time at the edge server can be formulated as.Therefore,the execution time of user k for edge computing is

Here,we ignore the time to retum the result to the user,because it is very short compared with the task transmission time and the task processing time.Besides,the transmission energy consumption of user k can be expressed as

2.3 Local Computing Model

fkdenotes the local computation resource of user k in CPU cycles per second.Therefore,the local computing latency of user k is defined as

In addition,we model the power consumption of local computing asfollowing reference [7],whereµis a power coefficient depending on chip architecture.Thus the energy consumption of user k for local computing is defined as

2.4 Problem Formulation

We use the system utility proposed in[7] as the performance metric to achieve the trade-off between the task execution time and energy consumption.Letd≜{dk}andF≜{Fk}.We formulate the system utility as

To maximize the system utility,this paper optimizes the offloading decision,SIC decoding sequence,computing resources,and transmission time allocation,for which the constrained optimization problem can be formulated as

The received power of the signal from user k should be less than the received power of the signal from user k-1(whose signal is decoded after user k).The constraint in (12) means that the computing resources allocated to users should not exceed the maximum computing resources available at the edge server.And the constraint in(13)means that the uplink transmission time cannot exceed the maximum transmission delay

III.PROBLEM ANALYSIS AND SOLUTION

The problem P1 is a 0-1 mixed-integer programming which is very difficult to solve.In this section,we divide problem P1 into two sub-optimization problems,i.e.a computational resource allocation problem and an offloading decision optimization problem.We first denote the set of users who choose to offload asO≜{k∈U|dk=1}

By substituting(3)(4)(5)(6)into(7).we can obtain in(14)

Sk,Ck,fkare fixed,If we want to get the,we can obtain the equivalent optimization problem as

Proposition 2.TheoptimalcomputationresourceallocationschemecanbederivedfromKKTconditions as

Proof.see appendix B.

Proposition 3.TheoptimalSICorderπ*isdeterminedsuchthat

denotes bkofuserkinoptima1SICdecodingsequence.Proof.see appendix C.

In order to get the sub-optimal transmission timeTt,*and the problem P2 can be simplified as

With the optimal solution (F*,π*,Tt,*) of P2,where theF*≜(k∈O) the offloading decision optimization problem can be modeled as

3.1 Transmission Time Allocation

We proposed an algorithm to solve the problem P3 to find the optimal transmission timeTt,*.We rewrite the objective function of problem P 3 as

We can derive the first order derivative and the second derivative of G(Tt)as

3.2 Offloading Decisions Optimization

Each user can choose to offload or not,thus there are 2Ncases in offloading decisions and we can traverse all possible cases to find the optimal one.However,with the number of users increasing,the computational complexity for the traversal search increases exponentially.

To reduce the computation complexity,we use the greedy idea to find a sub-optimal offloading decision,as illustrated in following Algorithm 2 to solve P4,in which we initialize a choice set M=U,i.e.,putting all users in M initially.At each step,we use the proposed Algorithm 1 to calculate the system utilityQ(O∪{k},F*,π*,Tt,*)(k∈M),and then we choose a user from the set M to execute task offloading to maximize the system utility.WhenM=Øor the system utility will no longer increase,the algorithm ends.The number of iterations of Algorithm 2 isThe maximum computational complexity of greedy algorithm isO(N2)

IV.SIMULATION RESULT

We setup a numerical simulation using MATLAB.An independent Rayleigh fading channel with average power loss being 10(－6)and channel bandwidth B=10MHz.The channel noise is modeled as white Gauss noise with power spectrum densityN0/2=10(－13)W/Hz.For user k,the number of CPU cycles to calculate 1-bit dataCk=1000cycles/bit,and the task size follows a uniform distribution withSk=300k bits.The local CPU computation capacity fkis randomly selected from the set{0.5,0.6,0.7,0.8,0.9,1.0}×109CPU cycles/second with a uniform distribution.

We use the traversal algorithm as the baseline to evaluate the proposed Algorithm 2.We set the maximum available computing resources at edge serverFmax=2 × 1010Hz.From Figure 1(a),we can see the system utility of Algorithm 2 is very close to that of the traversal algorithm.In addition,as illustrated in Figure 1(b),the computational complexity of the traversal algorithm increases exponentially as the number of users increases.On the contrary,the number of iterations of our Algorithm 2 increases quadratically.Therefore,the greedy algorithm of Algorithm 2 proposed in this paper can be regarded as an optimal scheme for computing offloading decisions.

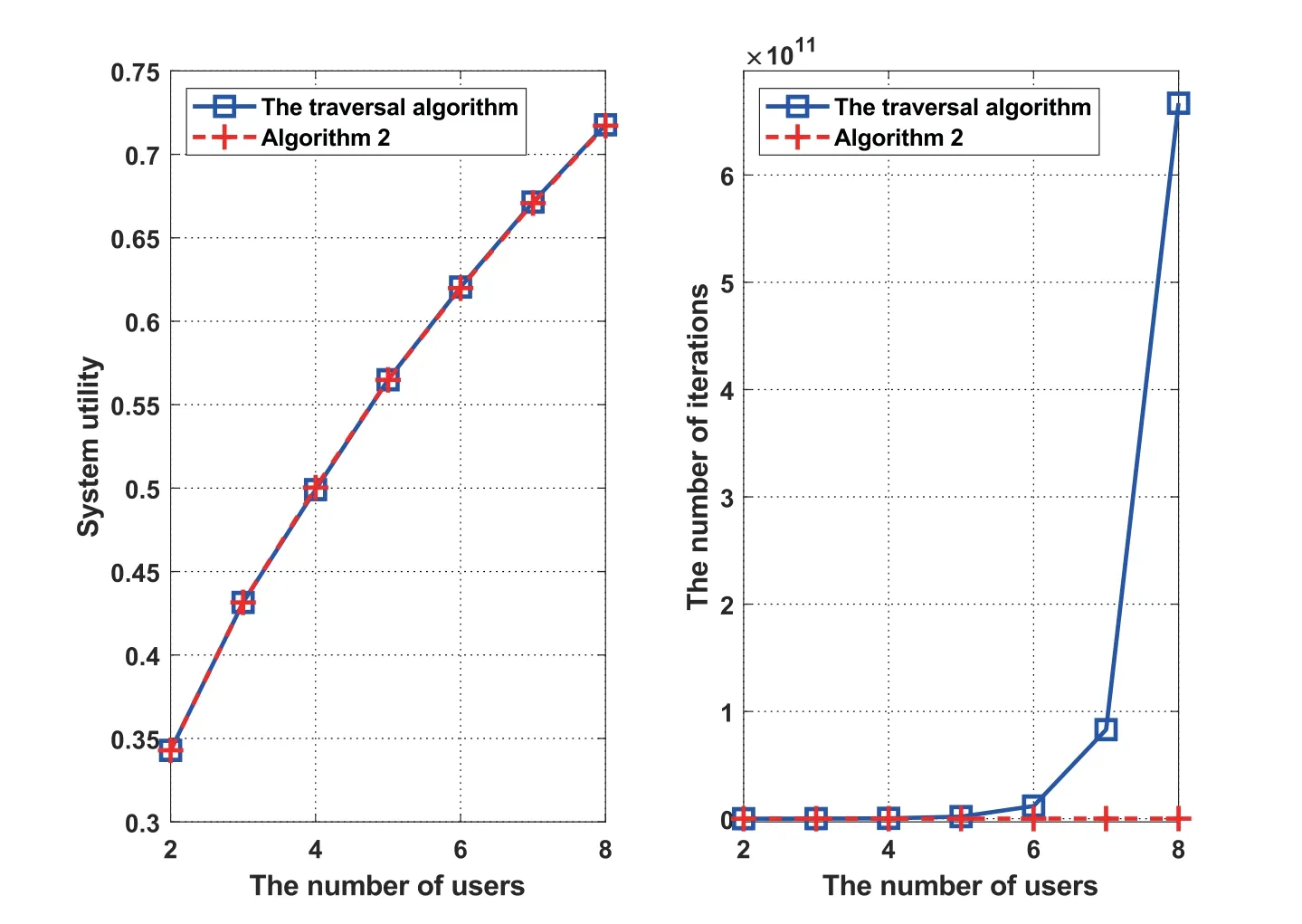
Figure 1.The performance and computational complexity of Algorithm 2 and the traversal algorithm.

Then,we compare the proposed NOMA-MEC offloading scheme with the existing OMA-MEC scheme.We setFmax=2 × 1010Hz.For the OMA-MEC,the TDMA model is used in which the uplink transmission of each user is independent and the transmission time of offloaded users is,whereis the uplink transmission time of user k.For the transmission time optimization in TDMA,we consider k independent sub-optimization problems,to easily solve them by the Newton method.

Three offloading schemes for NOMA or TDMA are considered.Scheme 1 is a full offloading idea in which all users offload their tasks to the MEC server.Scheme 2 is with the proposed Algorithm 2 to find optimized binary offloading.Scheme 3 is local computing without offloading.The system utility for Scheme 3 is always equal to 0 because there is no user choose to offload.

As illustrated in Figure 2,the proposed Algorithm 2,i.e.,Scheme 2 outperforms the other two schemes,and its system utility increases gradually as the number of users increases.The system utility for Scheme 1 increases within a limited number of users,i.e.,15 users in Figure 2,nevertheless,it decreases sharply after skipping over this point and even worse than the local computing Scheme 3,due to the limited radio time/spectrum and computing resources.Figure 2 also shows that NOMA scheme outperforms the TDMAOMA scheme due to its better spectrum efficiency.

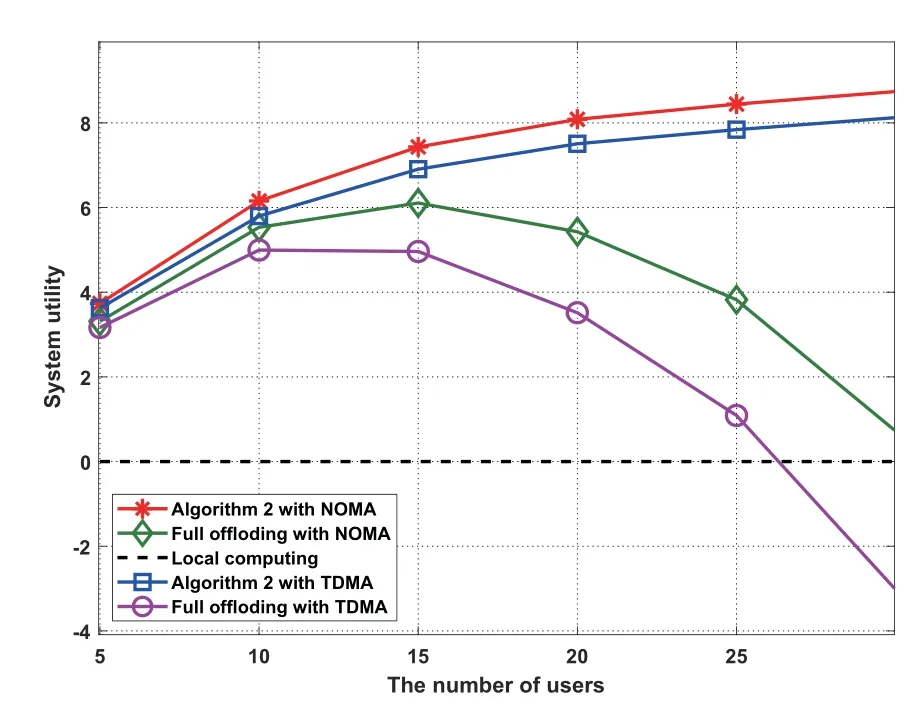
Figure 2.The system utility was obtained by three offloading decision schemes for NOMA and TDMA under a different numbers of users.

Finally,we compare the system utility performance of these OMA and NOMA schemes with server capability constraints from Hz to Hz and fixed 20 users,which is illustrated in Figure 3.We can see that the system utility of all schemes increases as server capacity increases,in which the NOMA schemes outperform their TDMA-OMA counterparts.

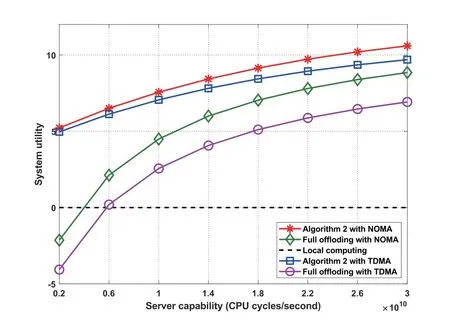
Figure 3.The system utility was obtained by three offloading decision schemes for NOMA and TDMA under different server capabilities.

V.CONCLUSION

We concentrate on the multi-objective optimization problem in a NOMA-MEC system with binary offloading.A system utility function is introduced as the performance metric to achieve the trade-off between latency and energy consumption for NOMAMEC system.An algorithm based on Newton method and greedy idea are proposed to maximize the system utility.Simulations show that the proposed algorithm is effective and the system utility of NOMA-MEC system is higher than that of TDMA-MEC system.

Appendix A.Proof of Proposition 1

According to Proposition 2 [11],User k’s minimum transmit-power is written as

signal to interference plus noise ratio(SINR)for user k’s transmission to the BS.Furthermore,given user k’s offloaded computation-workload.Sπ(k)and the uploading-duration Tt,we can derive k’s required SINRrπ(k)as

By substituting(18)into(19),we can obtain in(2).

Appendix B.Proof of Proposition 2

To solve the problem P 2,we need to first solve the following optimization problem.

This problem is a convex problem with one linear constraint and the Lagrangian function is

This problem is a convex problem with one linear constraint and the Lagrangian function is

We can easily getλ*＞0 anddue toFk＞0,then we have

Appendix C.Proof of Proposition 3

To find an optimal SIC orderπ*to minimize.Assuming that the offloading set O contains only two users,user 1 and user 2.If user 1 is decoded first,the weighted sum of minimum transmission powerP1→2is expressed as

And if user 2 is decoded first,P2→1can be expressed as

We can easily get when

userπ*(2)=user 1 andπ*(1)=user 2,and when

i.e.,userπ*(2)=user 2 andπ*(1)=user 1,which means that optimal SIC orderπ*is determined such that

Now we assume that the offloading set O contains three users,user 1,user 2 and user 3.user 1 and user 2 can be decoded as proved above.

userπ*(2)=user1 andπ*(1)=user3,Now compare user 3 with user 2

userπ*(3)=user 1,userπ*(2)

=uuser 2,userπ*(1)

=uuser 3 This conclusion can be easily extended to the multi-user scenario.