金属橡胶桥梁支座剪切屈服后刚度研究

黎大玮 夏修身 张永强 马健行 罗辉

摘要：

基于重叠面积法与Haringx理论，得到圆形截面金属橡胶桥梁支座剪切屈服后刚度的计算公式，公式中剪切屈服后刚度与压应力及支座直径成正比，与支座高度成反比，并且存在待求系数α与β。通过大尺寸金属橡胶桥梁支座试件的压缩及压剪试验，获得剪切模量与压缩模量之间的关系，求得系数α约为1.3。参考剪切试验中压应力、支座直径、相对密度和形状系数对支座剪切屈服后刚度的影响规律，给出无量纲系数β的计算公式。根据待求系数α与β，对理论计算公式进行实用性简化，并比较屈服后刚度的理论计算结果与试验结果。结果表明：实用计算公式与试验结果吻合较好，且具有较好的精度，可用于金属橡胶支座压剪状态下屈服后刚度的计算。

关键词：

桥梁支座; 金属橡胶; 屈服后刚度; 重叠面积法; 压剪试验

中图分类号： U443.361      文献标志码：A   文章编号： 1000-0844（2023）02-0355-07

DOI：10.20000/j.1000-0844.20220511001

Shear post-yield stiffness of metal rubber bridge bearings

LI Dawei， XIA Xiushen， ZHANG Yongqiang， MA Jianxing， LUO Hui

（School of Civil Engineering， Lanzhou Jiaotong University， Lanzhou 730070， Gansu， China）

Abstract：

Based on the overlapping area method and Haring theory， the formula for the shear post-yield stiffness of metal rubber bridge bearings with a circular cross-section was obtained in this study. The shear post-yield stiffness in the formula is proportional to the compressive stress and the bearing diameter and inversely proportional to the bearing height， where two coefficients α and β are to be determined. The relationship between the shear modulus and compression modulus of large-size metal rubber bridge bearing specimens was obtained through compression and compressive-shear tests， and coefficient α was approximately 1.3. Referring to the influence law of compressive stress， bearing diameter， relative density， and shape factor on the shear post-yield stiffness of the bearing in the shear test， the formula of the dimensionless coefficient β was evaluated. Furthermore， a practical simplification of the theoretical formulation was performed according to coefficients α and β， and the theoretical calculation results of the post-yield stiffness were compared with the experimental results. Results showed that the practical calculation formula， which agrees with the test results， is reasonably accurate. This formula can be used for the calculation of the post-yield stiffness of metal rubber bearings under compression-shear conditions.

Keywords：

bridge bearing; metal rubber; post-yield stiffness; overlapping area method; compression-shear test

0 引言

金屬橡胶桥梁支座是近期提出的一种支座，其具有承载能力高、阻尼大及抗腐蚀性好等优点，在中小跨公路桥梁中有较好的应用前景［1］。

目前，国内学者对金属橡胶构件的研究已取得一定的成果。江健等［2-3］对不同高宽比的空心圆形截面金属橡胶支座的剪切力学性能进行了试验研究，得到水平剪切刚度及等效阻尼比随支座高宽比、加载幅值及加载频率等参数的变化规律。王辰宇等［4］基于金属橡胶微观构造理论，研究得到金属橡胶的剪切本构力学模型，并进行了试验验证。袁泽森等［5］对两类加工工艺的金属橡胶支座进行压剪试验，并进行升温自恢复性能试验，结果表明两类支座都具有良好的耗能能力及自恢复性能。刘远方等［6］、郝慧荣等［7］对金属橡胶材料的迟滞振动恢复力模型进行了数值模拟研究，得到振动恢复力的组成及恢复力模型的适用性。夏修身等［8］对金属橡胶支座的隔震性能进行了振动台试验研究，结果表明支座的隔震性能良好。文献［9-11］开展了金属橡胶支座水平剪切性能试验研究，得到不同压应力下的滞回曲线，研究表明Bouc-Wen模型可以较好地模拟支座的水平滞回曲线。文献［12］对金属橡胶支座的压缩性能进行了研究，得到支座压缩性能的影响因素及变化规律。文献［13］对金属橡胶支座的转动性能进行试验研究，得到其转动力矩与转角的关系，可以满足桥梁转动的要求。目前开展的金属橡胶支座研究大多为试验研究，试验结果表明金属橡胶支座能满足桥梁正常使用时对支座力学性能的要求，但抗震设计时需要进行金属橡胶支座剪切屈服后刚度的理论计算，而目前此方面的研究尚属空白。

本文基于重叠面积法与Haringx理论，得到金属橡胶桥梁支座在压剪状态下剪切屈服后刚度的理论计算公式，并结合试验对公式进行验证。结果表明理论计算公式具有较好的精度，可用于金属橡胶支座压剪状态下屈服后刚度的计算。

1 屈服后刚度计算公式理论推导

基于重叠面积法［14］来描述金属橡胶桥梁支座压剪过程中的力学特性，并通过支座压缩性能与剪切性能之间的关系来推导支座屈服后刚度的计算公式。

如图1所示，设支座直径为D，水平剪切位移为u，则支座竖向临界承载力Pcr与竖向初始临界力Pcr0之间的关系如式（1）所示：

Pcr=ArAbPcr0 （1）

式中：Ab、Ar分别为支座横截面面积与重叠部分的面积。

由图1可以得到：

Ar=D24（π-2θ-sin2θ） （2）

θ=arcsinuD （3）

式中：θ为旋转角。

支座形状系数S按下式计算：

S=D/h （4）

式中：h为支座高度。

根据文献［15-18］中的Haringx理论，结合金属橡胶支座特殊的结构构造，初始临界承载力Pcr0为：

Pcr0=P2S+4PSPE-PS2β （5）

式中：β为无量纲系数;PS和PE分别为水平力和欧拉临界荷载：

PS=GAb （6）

PE=π2ErIsh2 （7）

式中：G为剪切模量;Is为截面惯性矩;Er为弯曲模量。

Er与压缩模量Ec有如下关系［15-17］：

Er=Ec/3 （8）

G与Ec之间存在以下关系：

Ec=αGS2 （9）

将式（6）～（9）代入式（5），有：

Pcr0=GπD28β1+απ2S412-1 （10）

联立式（1）与式（10）可得到：

Pcr=ArAbGπD28β1+απ2S412-1 （11）

压应力σ 的计算公式为：

σ=PcrAr （12）

剪切应力τ的计算公式为：

τ=FQAb （13）

式中：FQ为水平剪力。

剪应变γ的计算公式为：

γ=uh （14）

剪切模量G的计算公式为：

G=τ1-τ2γ1-γ2=ΔFQ·hΔu·Ab （15）

式中：ΔFQ为水平剪力变化量;Δu为水平位移变化量。

联立式（11）～（14），可得压剪状态下屈服后刚度Ku的计算公式：

Ku=ΔFQΔu=σπD22h1+απ2S412-1β （16）

根据重叠面积理论，推导得出了金属橡胶支座剪切屈服后刚度Ku的计算公式。由式（16）可知屈服后刚度与压应力、支座直径及支座高度有关，且式中还存在两个待求的无量纲系数α和β。

2 壓缩及压剪试验

2.1 支座试件

金属橡胶桥梁支座试件的材料为不锈钢金属奥氏体（06Cr17Ni10），金属丝丝径为 0.5 mm，螺旋直径为5 mm，采用缠绕、冷压等特殊工艺加工制作。

试验主要是求压缩模量Ec与剪切模量G之间的关系，并确定系数α和β。共设计了两组试件进行压缩及压剪试验，支座的设计参数如表1所列，支座试件如图2所示。

2.2 压缩试验结果

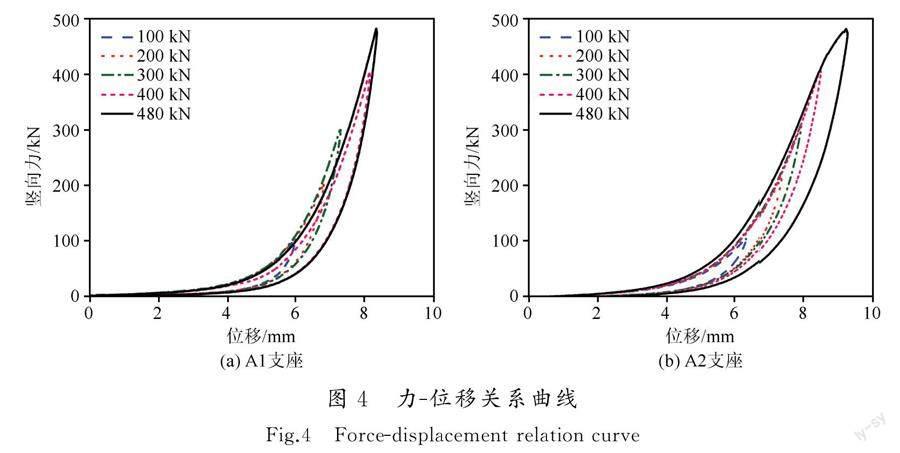
参照国家标准《橡胶支座第1部分：隔震橡胶支座试验方法（GB/T 20688.1—2007）》［19］，压缩试验在500 kN电子万能试验机上完成（图3）。试验加载速率为2 mm/min，试验中竖向压应力从0开始缓慢加载到最大。试验得到竖向压力与竖向位移的关系如图4所示。由应力-应变关系测得金属橡胶支座的切线模量，切线模量可以表示其竖向压缩模量。试验得到的压应力与压缩模量的关系如图5所示。

由图4可知，支座压缩加载曲线整体呈指数增长，在压缩试验过程中竖向荷载增加到480 kN（压应力为24 MPa），卸载之后支座未出现塑性变形，仍恢复为原状［12］。因此，该类大尺寸支座的竖向承载力设计值σu至少为24 MPa。

由图5可见，压缩模量Ec随压应力σ的增大而增大，即Ec与σ近似成正比，Ec还与支座的相对密度相关，越大，压缩模量Ec越大。从图5中取竖向压应力分别在4 MPa、6 MPa、8 MPa、10 MPa下的压缩模量Ec，并列于表2。

2.3 压剪试验结果

压剪试验装置如图6、7所示。采用电液压伺服作动器施加水平力，竖向千斤顶施加竖向力，分别使用压力环与位移计测定竖向力与竖向位移。电液压伺服作动器可提供的最大水平力为1 000 kN，行程为±200 mm;千斤顶可提供的最大竖向力为500 kN。试验采用位移加载控制，加载过程采取多次循环逐步加载的方式。

加载频率为0.016 Hz，剪应变为25%，竖向压应力分别为4 MPa、6 MPa、8 MPa、10 MPa时，A1支座的滞回曲线如图8所示。A2支座在剪应变为25%，加载频率为0.016 Hz，竖向压应力为6 MPa时的滞回曲线如图9所示。

由图8、图9可以看出，由于金属橡胶支座的特殊结构构造，剪切过程中支座先进入弹性阶段，支座承受的水平剪力达到屈服点进入屈服后阶段。从支座的滞回曲线可以看出，随着压应力σ的增大，金属橡胶支座内部金属丝接触增多，支座的水平剪切刚度也随之增大。结合式（17）计算其相应的屈服后刚度Kh，并列于表3。

Kh=Fi-FjUi-Uj （17）

式中：Fi，Fj为施加的水平力（Fi>Fj，i>j）;Ui，Uj为对应的剪切位移。

参照国家标准《橡胶支座第2部分：桥梁隔震橡胶支座（GB/T 20688.2—2006）》［20］，根据式（18）计算剪切模量G，并列于表3。

G=KhhAb （18）

3 理论公式与试验结果比较

根据表2、表3中由试验得到的压缩模量Ec与剪切模量G的关系，再结合表1中的S值，由式（9）可求出参数α，并列于表4。

由表4可知，α值在不同压应力下的变化较小，其均值约为1.3，因此文中参数α取1.3。

从图8及表3可以得到，屈服后刚度Kh随着压应力σ的增加而增加，因为压力会导致金属丝之间的接触增多，所以Kh增加的幅度也随压应力的增加而放慢。再结合文献［10］中金属橡胶支座屈服后刚度影响因素的试验研究结果，无量纲系数β计算时引入支座的形状系数S、竖向压应力σ、竖向承载力σu及相对密度，按下式计算：

β=（S）2+4.3σuSσ （19）

将α=1.3和式（19）代入式（16），由于1.3π2/12≈1且S41，故1+S4-1≈S2；再根据2.2节中试验结果，取σu=24 MPa，同样代入式（16），可得到：

Ku=πσD222h+163DS2 （20）

结合表1～表3，将其与试验的屈服后刚度值进行结果对比（表5、图10）。

由表5及图10可得到，在竖向压应力为4 MPa时，A1支座理论计算得到的屈服后刚度与试验值的差值最大，为4.2%;随着压应力增大，两者的差值明显减小，竖向压应力为6～10 MPa时两者差别在0.7%～1.3%之间。A2支座屈服后刚度的试验值和理论值在竖向压应力为6 MPa时的差值为1.6%。总的来看，理论计算的屈服后刚度与试验得到的屈服后刚度吻合较好，在5%以内，这表明文中提出的实用性计算公式可以用于金属橡胶支座处于压剪状态下的屈服后刚度计算，且具有较好的精度。

4 结论

（1） 基于重叠面积法与Haringx理论推导得到压剪状态下圆形截面金属橡胶支座的屈服后刚度计算公式，式中的屈服后刚度与压应力、支座直径及支座高度有关。此外，还存在两个待求的无量纲系数α、β。

（2） 通过压缩及压剪试验得到了4～10 MPa压应力下支座压缩模量Ec与剪切模量G的关系，再结合Ec与G的函数表达得到α的值约为1.3。

（3） 参考试验中支座相对密度、竖向承载力设计值及形状系数对屈服后刚度的影响，对比试验得到的屈服后刚度数值，引入系数β的计算表达式，对屈服后刚度理论计算公式的实用性作了进一步的改进。

（4） 屈服后刚度的实用计算公式与试验结果吻合较好，说明实用计算公式具有较高的精度，可用于金属橡胶支座压剪状态下屈服后刚度的计算。

由于文中的计算公式基于压剪状态推导而来，且需要一定的重叠面积支座才能屈服，因此其不能用于纯剪切下的屈服后刚度计算及弹性刚度计算，并且在低压应力下的计算误差相对较大。

参考文献（References）

［1］ 张颖周.新型桥梁支座力学性能试验研究［D］.蘭州：兰州交通大学，2018.

ZHANG Yingzhou.Experimental study on mechanical properties of new bridge bearing［D］.Lanzhou：Lanzhou Jiaotong University，2018.

［2］ 江健，周艳国，姚运生，等.不同高宽比金属橡胶隔震支座力学性能分析［J］.地震工程与工程振动，2015，35（3）：183-190.

JIANG Jian，ZHOU Yanguo，YAO Yunsheng，et al.An experimental analysis of the mechanical property of metal-rubber isolator with different aspect ratios［J］.Earthquake Engineering and Engineering Dynamics，2015，35（3）：183-190.

［3］ 江健.圆筒形金属橡胶隔震支座的隔震性能研究［D］.武汉：中国地震局地震研究所，2014.

JIANG Jian.An experimental analysis on the seismic isolation property of cylindrical metal-rubber isolator［D］.Wuhan：Institute of seismology，China Earthquake Administration，2014.

［4］ 王辰宇，彭文昊，李素超，等.基于统计接触特性的金属橡胶支座剪切本构关系［J］.工业建筑，2021，51（11）：25-30.

WANG Chenyu，PENG Wenhao，LI Suchao，et al.A constitutive model of metallic rubber bearings based on statistical contact properties［J］.Industrial Construction，2021，51（11）：25-30.

［5］ 袁泽森，刘振亮，李素超，等.形状记忆合金橡胶支座剪切性能及自恢复特性研究［J］.工业建筑，2021，51（11）：1-6，18.

YUAN Zesen，LIU Zhenliang，LI Suchao，et al.Research on shear properties and self-recovery characteristics of shape memory alloy pseudo-rubber bearings［J］.Industrial Construction，2021，51（11）：1-6，18.

［6］ 刘远方，白鸿柏，李冬伟，等.金属橡胶材料恢复力的三维模型［J］.振动与冲击，2011，30（8）：203-206，268.

LIU Yuanfang，BAI Hongbo，LI Dongwei，et al.Three diamentional model of restoring force of metal rubber material［J］.Journal of Vibration and Shock，2011，30（8）：203-206，268.

［7］ 郝慧荣，白鸿柏，候军芳，等.金属橡胶广义恢复力模型辨识［J］.振动与冲击，2008，27（11）：105-108，202.

HAO Huirong，BAI Hongbai，HOU Junfang，et al.Generalized resuming force model for metal-rubber［J］.Journal of Vibration and Shock，2008，27（11）：105-108，202.

［8］ 夏修身，張颖周，陈兴冲，等.金属橡胶支座力学性能试验［J］.长安大学学报（自然科学版），2019，39（4）：92-99.

XIA Xiushen，ZHANG Yingzhou，CHEN Xingchong，et al.Experiment on mechanical properties of mental rubber bearing［J］.Journal of Chang'an University （Natural Science Edition），2019，39（4）：92-99.

［9］ 杜骞，夏修身.金属橡胶支座剪切性能试验研究［J］.地震工程学报，2021，43（5）：1176-1182，1196.

DU Qian，XIA Xiushen.Experimental study on shear behavior of metal rubber bearings［J］.China Earthquake Engineering Journal，2021，43（5）：1176-1182，1196.

［10］ 孙森林.金属橡胶支座剪切性能研究［D］.兰州：兰州交通大学，2021.

SUN Senlin.Study on shear performance of metal rubber bearing［D］.Lanzhou：Lanzhou Jiaotong University，2021.

［11］ XIA X S，WU S W，SUN S L，et al.Lateral hysteretic behavior of a novel metal rubber bridge bearing［J］.Engineering Structures，2022，256.

［12］ 夏修身，张颖周.金属橡胶支座压缩性能试验研究［J］.应用基础与工程科学学报，2021，29（4）：952-960.

XIA Xiushen，ZHANG Yingzhou.Experimental study on compression performance of metal rubber bearing［J］.Journal of Basic Science and Engineering，2021，29（4）：952-960.

［13］ 夏修身，张颖周，杜骞.金属橡胶桥梁支座转动性能试验研究［J］.兰州交通大学学报，2021，40（1）：1-5.

XIA Xiushen，ZHANG Yingzhou，DU Qian.Experimental study on rotational performance of metal rubber bridge bearing［J］.Journal of Lanzhou Jiaotong University，2021，40（1）：1-5.

［14］ GAURON O，SAIDOU A，BUSSON A，et al.Experimental determination of the lateral stability and shear failure limit states of bridge rubber bearings［J］.Engineering Structures，2018（174）：39-48.

［15］ WEISMAN J，WARN G P.Stability of elastomeric and lead-rubber seismic isolation bearings［J］.Journal of Structural Engineering，2012，138（2）：215-223.

［16］ ZHOU T，WU Y F，LI A Q.Numerical study on the ultimate behavior of elastomeric bearings under combined compression and shear［J］.KSCE Journal of Civil Engineering，2018，22（9）：3556-3566.

［17］ GORDON P W，JARED W.Parametric finite element investigation of the critical load capacity of elastomeric strip bearings［J］.Engineering Structures，2011，33（12）：3509-3515.

［18］ 周通，李愛群.铅芯橡胶支座单元模型的开发及验证［J］.东南大学学报（自然科学版），2017，47（6）：1154-1160.

ZHOU Tong，LI Aiqun.Development and verification of element model for lead-rubber bearings［J］.Journal of Southeast University （Natural Science Edition），2017，47（6）：1154-1160.

［19］ 国家质量监督检验检疫总局，中国国家标准化管理委员会.橡胶支座 第1部分：隔震橡胶支座试验方法：GB/T 20688.1—2007［S］.北京：中国标准出版社，2007.

General Administration of Quality Supervision，Inspection and Quarantine of the People's Republic of China，Standardization Administration of the People's Republic of China.Rubber bearings—Part 1：seismic-protection isolators test methods：GB/T 20688.1—2007［S］.Beijing：Standards Press of China，2007.

［20］ 国家质量监督检验检疫总局，中国国家标准化管理委员会.橡胶支座 第2部分：桥梁隔震橡胶支座：GB/T 20688.2—2006［S］.北京：中国标准出版社，2006.

General Administration of Quality Supervision，Inspection and Quarantine of the People's Republic of China，Standardization Administration of the People's Republic of China.Rubber bearings—Part 2：elastomeric seismic-protection isolators for bridges：GB/T 20688.2—2006［S］.Beijing：Standards Press of China，2006.