基于BP神经网络PID控制对渔船冷库温度控制的研究

王佳豪，张存喜

（浙江海洋大学，浙江 舟山 316022）

0 引言

近年来，随着渔业生产情况、渔业市场的变化和我国渔船制冷技术与设备的稳定发展，国内新造和更新改造冷冻渔船的数量快速增加[1]。随着沿海地区渔业、捕捞业、渔船的不断发展，水产品的捕捞量大大提高，在储存运输过程中，渔船冷库制冷系统成为冷冻保鲜处理的关键设备。在远洋渔船中，冷库冷冻装置的性能和效率不仅仅影响渔获物的新鲜程度，而且直接影响渔船产量，特别是在渔业资源丰富海域附近作业捕捞的远洋作业渔船，其生产能力的大小直接取决于冷冻存储能力。虽然我国渔船制冷技术和设备近年来得到了较快的发展，但在渔船制冷设备上还存在着一些问题：温度调节主要由传统PID方式调节，该控制方式波动性大、不稳定、反应能力慢，不仅无法控制水产品的最佳保鲜温度，而且容易导致能源浪费，无法达到节能环保的作用。

在渔船运输、冷冻保鲜中温度是一个非常重要的因素，直接影响着渔船的产能及品质，一种好的温度控制算法既能保证温度的稳定性，又能将能耗控制在最低范围内，从而可以大幅度地提高产能并且节省成本，使渔船捕捞达到更大的效益。因此对渔船冷库制冷温度控制策略展开研究对当前国内渔业制冷发展具有重要的指导意义。为此，本文以渔船冷库环境中温度为研究对象，利用智能BP神经网络算法的高稳定性和高鲁棒性，在传统的PID温度控制中引入了该智能算法，且寻找到此算法的最优参数比例，使渔船冷库温度控制器达到既能保证温度稳定又能降低能源消耗的效果。

1 渔船冷库温度控制传递函数建立

1.1 渔船冷库制冷原理

根据文献调研分析和对渔船冷库的实地了解，目前渔船冷库的温度控制还是以传统蒸汽压缩的方式为主，主要工作设备是蒸汽压缩机、气体冷凝机、节流元件及蒸发组，其中该压缩机中的制冷剂为氨气。整套氨气压缩热循环控制原理为：制冷剂氨气被吸入蒸气压缩机中处理后变成高温、高压的气体，该气体再进入气体冷凝机中进行冷凝放热并变成液体，此液体慢慢流过节流装置，降温、降压并释放为湿蒸气，最后进入蒸发组液体汽化吸收大量热量，使冷库环境迅速降低，达到制冷效果[2]。

1.2 渔船冷库温度控制传递函数建立

本文将以渔船冷库温度控制系统为研究对象，根据能量守恒定律，冷库内温度热量传递，以冷库环境内外热量流入、流出差来表达，可得

式中：C为冷库内气体比热容，kJ/K；To为冷库外的环境气温，K；Ti为冷库内的被控气温，K；H为冷库内热传导系数，W/（m2·K）；Q为单位时间内产生或者消耗的能量，kJ/s；A为传导面积，m2。

当冷库温度稳定时，则有dT/dt=0，令T=C/（HA），K=1/（HA），冷库内的温度Ti与通过制冷设备所产生的能量Q都达到稳定状态，即Ti=Ti′，Q=Q′。

将上述稳定状态能量代入式（1）得到

当系统处于调整控制状态时，Ti=T′+ΔT，Q=Q′+ΔQ。

将上述调整控制状态能量代入式（2）得到

因此，可以得到冷库内的被控温度的变化量ΔT与温度控制量ΔQ之间的传递函数为

根据相关资料了解学习，一般的渔货品海鲜（本文不考虑特殊渔获品超低温冷库冷藏情况，如金枪鱼只有在-60～-80 ℃超低温环境才能长期存放）存放冷库的最佳冷冻温度为-18～-23 ℃，冷库外的环境温度一般为15～20 ℃，得出惯性时间常数T=88/N≈400 s，取导热系数H=0.05，根据温度控制差值和传热面积得出系统增益K=1.1，不考虑其他因素。

综合上述分析可得，渔船冷库温度控制的传递函数为

2 BP神经网络PID温度控制研究

2.1 温度控制种类及传统线性PID控制原理

根据相关资料学习，国内外在温度控制应用中目前有以下的几种控制方式。

1）传统线性PID控制。在工业控制中和流程行业过程控制中较为多见，主要是通过改变PID的3个参数（比例系数、积分系数、微分系数）使得它们达到一个相互协调、相互制约的状态，进而使得系统达到更快、更准、更稳的控制目标，但存在无法实时精准调控的问题。

2）位式加热控制。其原理是实际测得的温度比设定的最低温度低时，系统开始加热升温；当实际测得的温度超过了设定的最高温度时，停止加温，不足之处是反应速度慢、不够精准、能源消耗大。

3）模糊逻辑控制。该控制技术是一种依赖于计算机数字，靠模糊语言变量、模糊集合论和模糊逻辑推理等理论基础的控制算法，具有将复杂系统简单化、方便进行人机对话、鲁棒性和自适应能力强等特点，但模糊逻辑推论较难且适用于大范围多对象控制。

4）模型预测控制。是目前较为先进的一种控制算法，具有不断循环优化的特点，使用在滞后性较大的控制场合效果显著，存在难度较大、成本高的问题。

5）智能数字PID控制。这是一种将人工智能控制算法与传统PID控制相结合的控制算法，不仅能最大程度地体现传统控制“

快、准、稳”的优点，还能进行适时调控。随着人工智能技术的发展，这种控制在生产中使用得越来越多，其中BP神经网络算法也是其中的一种。

在渔船冷库温度控制系统中，大多数渔船一般采用传统的利用反馈对控制过程进行调节的线性PID温度控制器[3]。该控制器一般通过改变比例系数、积分时间常数、微分时间常数来进行控制调节，其传统PID控制结果框架如图1所示。

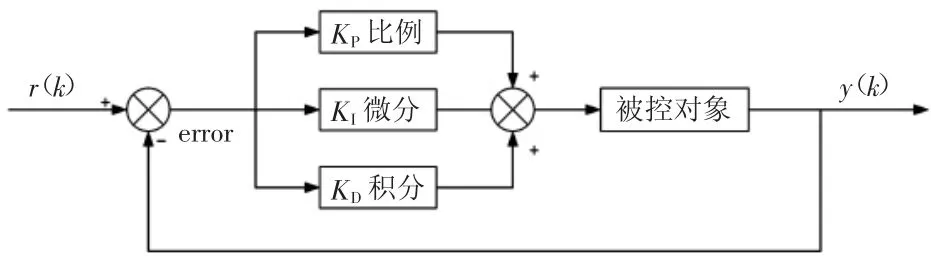
图1 传统PID控制原理框图

其数学表达式为

式中：Kp为比例系数，Ti为积分时间常数，Td为微分时间常数。

传统的PID控制对渔船冷库温度控制时，由于3种参数不能实时进行调节，导致其控制过程存在不稳定、鲁棒性差的情况[4]。

2.2 BP神经网络结构及算法

为了解决我们研究的渔船冷库温度控制缺陷问题，获得更好的温度控制效果，控制器必须能使3种参数实时完成相互协调制约。为了能寻找到这3种参数的最佳组合，本文在传统PID控制中引入了智能数字PID控制中的BP神经网络算法[5]。

BP神经网络概念最早是20世纪80年代Rumelhart和McCelland两位科学家带领的研究小组提出，主要内容是把实际输入值与设定值进行差值反向传播，然后进行自我学习的一种多层前馈网络，具有理论模型结构简单、算法简洁明了的优点，其算法模型如图2所示。

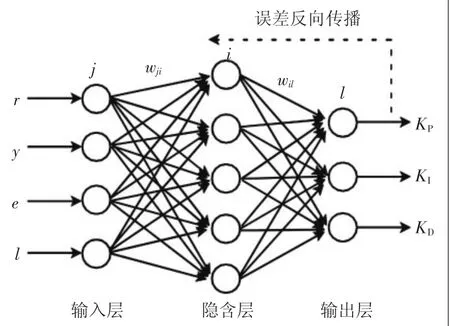
图2 三层BP神经网络结构

三层BP 神经网络结构[6]数学表达式如下：

神经网络输入层的输入层公式为

神经网络隐含层的输入层公式为

神经网络隐含层的输出层公式为

采用S型函数[7]作为隐含层神经元的激活函数为

则推导出神经网络输出层权重系数的算法为

同理可得隐含层权值系数的算法为：

输出层的3个神经元节点输出分别对应PID控制器中的3个可调参数：比例系数Kp、积分系数Ki、微分系数Kd。

采用非负S型函数作为输出层神经元的激活函数。

BP神经网络传递过程中，还存在反向的输出层与修正层之间的传递，取其性能函数为

其中增加动量项公式将降低网络对本地细节的敏感性，从而降低网络陷入本地的风险最低限度，快速找到全局最小值[8]，可采用以下公式：

式中：α为动量系数，η为学习率，范围都在0～1内；k为学习次数。其中微分展开：

其中，∂y（k）/∂u（k）可近似用符号函数sgn（∂y（k）/∂u（k））代替。

由上述推论可得以下公式：

神经网络输出层权值算法为：

隐含层加权学习算法为：

式中：g′（x）=g（x）［1－g（x）］，f′（x）=［1－f2（x）］/2。

2.3 BP神经网络PID温度控制器

将以上BP神经算法引入传统PID控制器中，依据系统不同时刻的运行状态，对传统PID控制器的3种参数进行不停的整定，达到最满意的系统输出为止。整个过程其实是对BP神经网络里面的隐含层和输出层的加权系数进行调整，使BP神经网络的输出层的3个PID参数能达到使系统最理想的控制状态[9]，如图3所示。

3 仿真研究与结果分析

3.1 BP神经网络PID控制器与传统PID控制器比较研究

为比较传统PID控制器和加入BP神经网络PID控制器对渔船制冷温度的控制效果，采用上述推导的温度传递公式对制冷温度进行仿真研究[10]。根据上述推导的温度控制传递函数，进行BP神经网络PID控制与传统PID控制设计，进行仿真研究对比，纵坐标为冷库温度，横坐标为仿真反应时间。因为该系统的环境温度变化较慢、惯性时间常数较大，将系统仿真运行的时间设置为2500 s，以便更好地观察仿真曲线结果。其中将系统仿真环境初始温度设置为20 ℃，冷库期待稳定值温度设定为-20 ℃，仿真研究结果如图4所示。

从图4所示的仿真曲线可以看出，BP神经网络PID控制器曲线呈不断稳定起伏状态，而传统PID控制器曲线波动幅度大，且超调量差值远远大于BP神经网络控制器。传统PID控制器在530 s左右达到温度最低值-32 ℃，超过温度稳定值60%，控制过程中波动很大；而基于BP神经网络PID控制器在120 s左右达到温度最低值为-22 ℃，超过温度稳定值10%，且后续时间处于持续稳定状态，明显比传统PID控制器的幅度小很多。由图4得出，传统PID控制器的达到稳定温度（振幅不大于2%）的时间为2000 s，而基于BP神经网络PID控制器到达稳定温度的时间为1000 s，基于BP神经网络PID控制器的调整时间比传统PID控制器快了1000 s，这说明基于BP神经网路PID控制器系统运行时能更快地到达稳定状态。

由上述仿真研究结果分析可知，引入智能BP神经网络算法的PID控制器比传统温度PID控制器有着更高的稳定性和鲁棒性，该控制器更适用于渔船冷库温度控制。

3.2 BP神经网络PID控制器最优参数输出值研究

该设计控制不仅要求此控制器具有更稳定的性能，而且还需要设定参数最佳值保证温度控制过程达到最节能的状态。为了寻找最佳比例系数Kp、积分系数Ki、微分系数Kd，对3个参数在BP神经网络输出进行分别仿真研究，得到3种参数输出值曲线，如图5～图7所示。

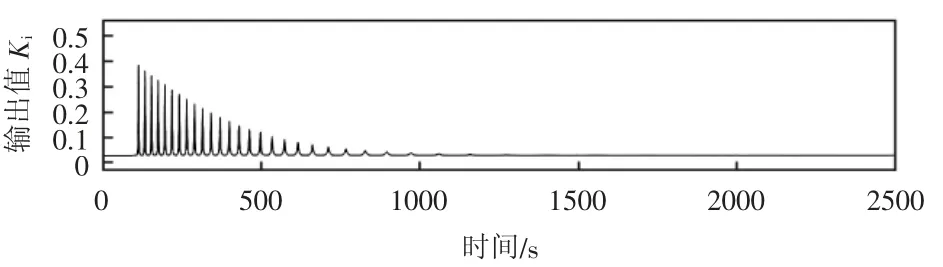
图6 BP神经网络积分系数Ki输出曲线

图7 BP神经网络微分系数Kd输出曲线

从图5～图7中可以看出，BP神经网络算法输出的比例系数Kp、积分系数Ki、微分系数Kd一直在不断调整，直至得到一个稳定的值，根据最终曲线稳定，得到3种参数最佳稳定值为：比例系数Kp=0.4977，积分系数Ki=0.0013，微分系数Kd=0.3950。

综上所述，与传统的温度PID控制器相比，引入BP神经网络PID控制器的鲁棒性、稳定性更强，具有更强的抗干扰能力，而且得到该PID控制器3种参数的最佳比例组合（比例系数Kp=0.4977，积分系数Ki=0.0013，微分系数Kd=0.3950）。在该参数组合下，BP神经网络PID控制器不仅能对一些不确定情况的干扰进行实时调整，达到自适应能力强的状态，而且整个控制器的能耗和输出达到最优值。

4 结语

本文以渔船冷库温度控制为对象展开研究，利用BP神经网络复杂的非线性映射能力与传统PID控制器结合，设计了基于BP神经网络PID控制，并推导出函数算法，通过对其仿真分析，验证了基于BP神经网络PID控制在渔船冷库温度这种多变量的稳定性、滞后性和实时性的控制上明显比传统PID控制器控制效果更好，得出了PID的3种参数的最优输出值。在此设定下的BP神经网络PID控制器既能保证渔船冷库温度的稳定性，又能将能耗控制在最低范围内，大幅度提高产能和节省成本，对渔船制冷发展具有一定的意义。