基于多岛遗传算法的干式空心电抗器热磁联合优化方法

袁发庭，韩毅凛，唐波，姜发，杨文韬，王玥，黄力

（1.湖北省输电线路工程技术研究中心（三峡大学），湖北 宜昌 443002；2.三峡大学电气与新能源学院，湖北 宜昌 443002）

0 引言

空心电抗器作为电力系统重要的感性元件，具有结构简单、线性度高和免维护等特点，在输电系统中被广泛应用。对于大型电力电抗器而言，通常采用增加包封线圈的匝数、半径及降低高度等方法来实现电感守恒，采用增加气道宽度和包封数量等方法来提高通流能力，然而上述方法必然造成金属导体用量的显著增加［1-3］。因此为了减少电抗器的金属导体用量，开展空心电抗器包封线圈散热特性及整体结构优化设计至关重要。

温升计算是获得电抗器散热特性的前提，目前一般是运用平均温升法、有限差分法和有限元法等开展研究。1）平均温升法：文献［4］选取干式空心电抗器进行温升实验，通过作图法和公式计算法确定绕组电阻，根据温升与电阻关系计算得到平均温升。文献［5］给出了空心电抗器绕组平均温升的解析式，但平均温升无法反映电抗器具体部位温升分布情况。2）有限差分法：文献［6］研究了电抗器包封线圈的散热过程，利用传热学准则式得出了包封壁面对流换热系数，结合有限差分法得到了电抗器温升分布，但是该方法未能考虑包封壁面热流密度分布对计算温升的影响。3）有限元法：文献［7-12］建立了电抗器二维仿真模型，采用有限元法得到了包封温度分布，但该方法忽略了星形架等的影响。文献［13-16］建立了空心电抗器三维模型，通过有限元法得到了电抗器的温度场，实验测量结果验证了仿真计算的准确性。上述方法能够获得电抗器准确的温升分布，但未考虑包封线圈与气道间的散热过程，无法实现包封线圈热效率的优化。

在电抗器优化方面，目前的研究工作主要有：1）电磁优化方面：文献［17］从电抗器电感实现的本质出发，将结构复杂的电抗器等效为单个线圈，在保证电感恒定的前提下，得到了最佳的金属导体用量。文献［18］通过在导线芯外层增加磁粉层的方法减少电抗器金属导体的用量，并建立相应的模型验证了结论的正确性，然而上述方法未考虑结构调整对电抗器温升的影响。2）热效率优化：文献［19］提出了等电流密度法，可以保证电抗器各包封线圈具有相同的载流利用率，基于此，文献［20］提出了结合平均温升的等电流密度法，能够实现各包封平均温升基本相等。文献［21］运用有限元法，调整气道宽度、线圈厚度以匹配包封-气道的生热散热能力，获得了最佳的气道宽度，但该方法是基于有限元仿真软件开展的参数优化，其计算量大，现阶段难以推广使用。3）在整体优化方面：文献［22-23］采用遗传算法或粒子群算法等对电抗器进行优化，提高了电抗器金属导体利用率。然而，上述方法通过调整电抗器结构参数以达到降低优化金属导体用量时，未能全面考虑结构参数对电感、温升和损耗的影响［24-27］。

本文基于干式空心电抗器的设计参数，在COMSOl 仿真软件中建立了电抗器三维模型，通过流场-温度场耦合得到了包封线圈温升。提取了包封线圈和气道的温度、流速分布，得到了包封线圈和气道间的散热特性。在此基础上，选取包封线圈-气道单元温升反映电抗器整体温升，结合竖直管道对流换热实验关联式，推导出电抗器的温升计算方法。联立电抗器电感守恒和结构方程，得到电抗器金属导体用量、损耗与包封线圈整体外形比例、气道宽度和包封数量等参数间的关系式。以电抗器金属导体用量最小为优化目标，采用多岛遗传算法得到了结构参数的最优解，优化方法能显著降低电抗器金属导体用量，对指导电抗器的优化设计具有重要意义。

1 电抗器流场-温度场耦合仿真计算

1.1 温度场仿真模型的构建

图1 所示的电抗器电气参数为：额定电压值和电流值分别为220 kV 和1 600 A，电感值为12 mH。其中，干式空心电抗器主要由包封线圈、星形架和撑条组成。包封线圈在电气上呈并联连接，各包封线圈间由撑条隔开形成气道，起到绝缘和散热的作用。包封线圈一般由多根并联的圆导线或扁导线组成，导线外有绝缘材料包裹。星形架分布在电抗器的顶端和底端，起到分配各包封线圈电流和加固电抗器的作用。

图1 空心电抗器基本结构Fig.1 Basic structure of air core reactor

包封线圈结构参数为：R内=0.3 m，R外=1.0 m，H=1.5 m，d=0.03 m，包封数量为12 个。星形架结构参数为：K1=2.0 m，K2=0.1 m，星形架数量为8个。

根据干式空心电抗器的结构特点，在流场-温度场耦合仿真计算中，考虑到计算准确性和计算时长，作以下假设：忽略包封线圈间撑条对温度的影响，只考虑包封线圈和星形架，建立三维模型。整个计算域设置为正方体，边长为6 m。

温度场仿真时的边界条件设置如下：电抗器包封线圈和星形架为静止壁面，各方向速度均为0；整个模型下底面设置为入口，且速度为0，静压力为0；前后侧面、左右侧面和上表面设置为出口，法向速度为0，静压力为0；环境温度设置为20 ℃；考虑到最外最内包封线圈和星形架表面的热辐射过程，设置其表面发射率为0.9。该模型通过加载体积力的方法进行温度场仿真计算。边界条件如图2所示。

图2 电抗器温度场计算域各参考边界Fig.2 Reference boundary of reactor temperature field calculation domain

1.2 损耗计算方法

为得到电抗器损耗分布，需先准确计算磁通密度的分布。因此根据电抗器结构特点建立了电抗器磁场仿真模型。由各包封线圈电流获得了包封线圈周围磁通密度分布，如图3所示。

图3 电抗器磁场仿真结果Fig.3 Simulation results of reactor magnetic field

根据上述磁场仿真结果，结合包封线圈结构参数求得涡流损耗，则包封线圈总损耗为涡流损耗与电阻损耗之和。同理，根据星形架结构尺寸，结合流过的电流和周围磁场的分布，可以计算得到星形架上总损耗。

1.3 温度场仿真结果

根据流场-温度场计算方法可以得到电抗器温度场仿真结果如图4所示。仿真总时长设置为10 h，步长设置为0.1 h，容差设为0.05，在10 h 时电抗器温度已经达到稳态，环境温度设为20 ℃。

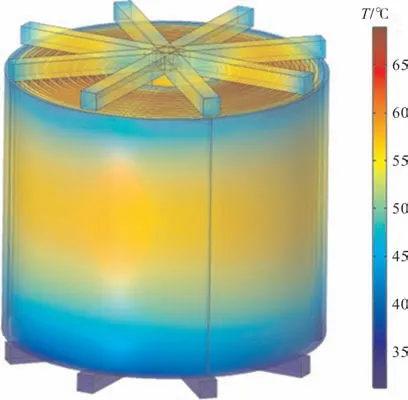
图4 温度场仿真结果Fig.4 Simulation results of temperature field

考虑到网格剖分的疏密和星形架对电抗器温度场的影响，分析了不同网格划分和加装星形架对电抗器温升的影响规律。

1）根据上述计算方法，得到不同网格剖分下电抗器最高温升如表1所示。

表1 不同网格划分对温升影响Tab.1 Influence of different meshes on temperature rises

由上表可知，当网格数达到446 828 时，最高温度已经稳定不变，此时温度为66.0 ℃，因此该网格数量满足温度场计算精度要求。

2）基于上述的方法，给出了加/未加星形架下电抗器温度场分布结果，其中未加星形架的温度场仿真结果如图5所示。

图5 未加星形架下电抗器温度场仿真结果Fig.5 Simulation results of reactor temperature field without spider arm

根据图4—5 的温度场仿真结果，提取了在星形架正下方和不在星形架正下方轴向方向的两种路径。轴向方向上在星形架下方和不在星形架下方两种路径下的温度分布，选取路径如图6 所示，根据图6 所选取的路径得到了电抗器温度分布曲线如图7所示。

图6 提取的路径Fig.6 Extracted path

图7 不同路径下温度分布曲线Fig.7 Temperature distribution curves under different paths

由图7 可知，加和未加星形架时电抗器包封线圈温升分布基本相同，最高温度均为65 ℃左右，星形架对电抗器温度的影响较小，可忽略不计。其主要原因是星形架的损耗占电抗器包封线圈的总损耗比例较小。

2 包封线圈-气道单元散热特性研究

基于图4 中电抗器三维温度场分布，利用仿真软件后处理功能，选取内部包封5、6 和7 开展研究。选取的3个包封温度分布如图8所示。

图8 包封线圈的温度分布Fig.8 Temperature distributions of encapsulated coils

由上图可知，内部包封线圈5、6和7的温度分布基本相同，最高温度约为65 ℃。沿轴向方向包封线圈温度呈先升高后逐渐降低的趋势，其最低温度都接近环境温度且出现在底部，最高温度位于包封线圈顶端10%～20%位置处。

为了分析空心电抗器内部包封线圈散热特性，提取在包封线圈最高位置和中轴线位置的温度和流速分布。选取的路径如图9所示。

图9 选取的路径示意图Fig.9 Schematic diagram of the selected path

2.1 温度分布

1）根据温度场仿真结果提取图9 路径所示的径向温度分布如图10所示。

图10 最高位置处温度分布Fig.10 Temperature distribution at the highest position

由图10可知，2到11号包封沿径向方向温度分布基本一致。同时，最内最外包封线圈温升明显低于内部包封线圈，其原因在于最内包封线圈内侧和最外包封线圈外侧的散热条件为大空间对流散热，相比于内部包封线圈散热条件更好，温升较低。

2）根据温度场仿真结果提取图9 所示的轴向温度分布如图11所示。

图11 不同包封温度沿轴向分布Fig.11 Temperature distributions along the axial direction of different encapsulation

由图11 可知，第5、6 和7 包封在同一高度处温度基本一致。第5、6和7包封在轴向温度先逐渐升高而后下降，在高度为1 m 开始有下降趋势，其主要原因是电抗器线圈端部具有更好的散热条件。

2.2 流速分布

根据温度场仿真结果，提取电抗器在图9 径向处包封线圈间气道内流体流速分布，如图12所示。

图12 最高位置处流速分布Fig.12 Velocity distribution at the highest position

由图12 可知，包封1 和包封2 间气道到包封11和包封12 间气道流速在0.8 m/s 到1 m/s 之间波动，其数值非常接近。靠近最内和最外包封线圈流速明显较低，其原因在于，最内最外包封线圈一侧为大空间散热，内部包封线圈一侧为气道散热。

3 电抗器热磁联合优化方法

3.1 电抗器最高温升恒定

根据上文电抗器温度场仿真结果可知，内部包封线圈2—11 的温度分布及最高温升基本相同。故选取图13所示的线圈-气道单元来表示最高温升。

图13 包封-气道单元Fig.13 Encapsulation-air duct unit

根据图10 提取的电抗器内部包封温度分布可知，内部包封线圈的最高温升相同，即可认为包封2 到包封11 产生热量的能力基本一致，对外散出热量的能力也基本一致。由物理学知识可知，包封线圈顶端温升可近似表示为式（1），即表示为流体温升和流体与包封线圈温度差之和［24］。

式中：H和d分别为高度和气道宽度；Tmax为包封线圈的最高温度；和ρ分别为流体（即空气）的平均流速和密度；Cp和λ分别为空气的比热容和导热系数；Nu为对流换热努塞尔数；qw为传热热流密度，如式（2）所示［24］。

式中：kc为电抗器的损耗系数即电阻损耗和涡流损耗之和与电阻损耗的比值；a和b分别为单匝导线的径向宽度和高度；I为流过包封的电流；γ为金属导体电导率。

式（1）为包封线圈-气道单元热流密度表达式，认为在调整线圈结构过程中，电流分配方式不改变，且包封数量变化与包封电流变化成比例关系，则包封电流变化率如式（3）所示。

式中：kI和km分别为电抗器包封电流变化率和包封数量变化率；m为包封数量。

采用归一化的研究：设调整线圈某参数X为X'，则称kX=X'/X为参数X变化后与变化前的比例。X表示线圈外形描述系数或相关物理量，如包封数量、包封径向宽度、包封电流等。

假设在调整过程中，由于包封线圈温度在一定的范围内可以认为金属导体电导率γ和损耗系数kc保持不变。联立式（2）—（3），则包封数量变化对热流密度变化率如式（4）所示［25］。

联立式（1）和式（4），故在自然风冷情况下，考虑气道宽度和包封数量变化的包封线圈最高温升变化率如式（5）所示［25］。

3.2 电抗器电感守恒约束

由电感实现方式可知，若图14 中两种不同方式绕制的线圈中通过的电流一致，且产生的磁场能量也相同时，那么可以作如下等效。

图14 电抗器等效厚壁线圈Fig.14 Equivalent thickness wall coil of reactor

由图14 可知，定义电抗器外形尺寸比例系数α和β为［24］：

式中α和β分别为电抗器高度H和厚度THi与平均直径Dav的比值。

为保证电抗器在优化前后电感值保持恒定，电磁效率的约束方程采用下式表示［24］。

式中L和分别为电抗器的电感值和线圈平均匝数。

式（7）揭示了电抗器电感与厚壁线圈平均匝数，直径和高度之间的关系，是热磁联合优化中的电感守恒方程。

3.3 电抗器结构方程

结合图13 和图14 可知，等效线圈的结构方程可以表示为式（8）［25］。

调整电抗器结构必然导致电抗器高度、平均直径和线圈厚度变化。定义α'为调整后电抗器高度与平均直径的比值，β'为调整后电抗器线圈厚度与平均直径比值，如式（9）所示。

式中H'、和分别为变化后的电抗器高度、厚度和平均直径。

图13中气道宽度d的变化会影响电抗器整体结构，图14 中包封数量m的调整对电抗器尺寸同样产生影响，联立式（6）、式（8）—（9）可知。

3.4 热磁联合优化方法

联立式（5）—（9），在保证电抗器电感和最高温升条件的前提下，其热磁联合优化方程如式（11）所示。

根据电抗器的初始设计参数，在上述方程中包封线圈高度H=1.5 m，气道宽度d=0.03 m，外形尺寸比例系数α=1.2，β=0.5，其中流体特性参数如下，导热系数λ=0.03，比热容Cp=1 022 W·kg-1·K-1，流体密度ρ=0.94 kg·m-3。

导体用量变化率可表示为kMass=kakbkDavk-Wkm。在额定电流不变的情况下，损耗变化率可由电阻变化率表示。即损耗变化率可由kR=kDavk-W/kakbkm表示。联立式（11），则kMass，kR可由α'、β'、kd、km表示，如式（12）所示［25］。

3.4.1 结构参数对导体用量变化率的影响

1）α'和β'对导体用量变化率kMass的影响。

由图15可知，随着α'增大，kMass逐渐降低而后趋于稳定。在α'取得1.2时，kMass取得最小值0.61；同时随着β'增大，导体用量变化率kMass逐渐升高。在β'取得0.20时，kMass最小值为0.61。

图15 α'和β'对金属导体用量变化率的影响Fig.15 Effect of α' and β' on the amount of metal conductor

2）kd和km对导体用量变化率kMass的影响。

由图16 可知，随着kd增大，导体用量变化率kMass逐渐降低。在kd取得1.1 时，kMass最小值为0.52；同时随着km增大，导体用量变化率kMass逐渐降低，在km取得1.16时，kMass最小值为0.58。

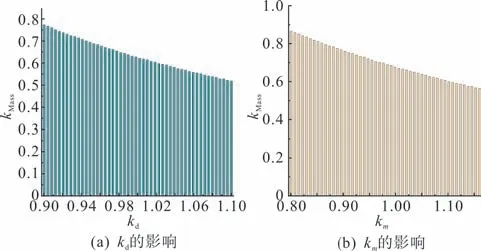
图16 kd和km对导体用量变化率的影响Fig.16 Effect of kd and km on the amount of metal conductor

3.4.2 结构参数对损耗变化率的影响

1）α'和β'对损耗变化率kR的影响。

由图17 可知，随着α'增大，损耗变化率kR逐渐升高。在α'取得1.60 时，kR最大值为0.69；同时随着β'增大，导体用量变化率kR逐渐降低。在β'取0.20时，kR最大值为1.80。

图17 α'和β'对损耗变化率的影响Fig.17 Effects of α'and β'on the rates of loss

2）kd和km对导体用量变化率kR的影响。

由图18 可知，随着kd增大，损耗变化率kR逐渐升高。在kd取得1.10 时，kR最大值为1.91；同时随着km增大，损耗变化率kR逐渐升高。在km取得1.16时，kR最大值为1.93。

图18 kd和km对损耗变化率的影响Fig.18 Effect of kd and km on the rate of loss

3.4.2 热磁联合优化结果

由上述单个因素对导体用量变化率影响可知，在不考虑kd和km时，当α'=1.2，β'=0.2 时，金属导体用量达到最小。故应考虑此时，kd和km对导体用量变化率影响。根据上述的电抗器热磁联合优化方法，可以获得电抗器金属导体用量变化率、损耗变化率与各变量参数间的优化云图，如图19—20所示。

图19 kd和km对导体用量变化率kMass的影响Fig.19 Effect of kd and km on the amount of metal conductor

由图20 可知，在其他参数保持恒定的条件下，随着气道宽度和包封数量的增加电抗器金属导体用量逐渐减少，此时损耗逐渐增大。结合图15 到图20热磁联合优化结果表明，在电抗器金属导体用量达到最小值时，损耗达到原来的2.3倍。

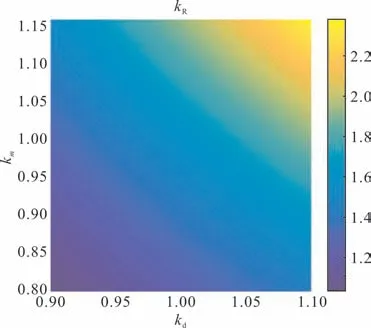
图20 kd和km对损耗变化率kR的影响Fig.20 Effect of kd and km on the change rate of loss kR

4 基于多岛遗传算法的干式空心电抗器优化

由上述热磁优化结果可知，当电抗器金属导体用量达到最小值时，损耗显著增加，为降低金属导体用量的同时使得电感，温升和损耗满足设计要求，采用多岛遗传算法得到最优解。

4.1 多岛遗传算法

遗传算法（GA）是基于自然界中生物进化过程染色体交叉变异等规律设计的，相比于其他的优化算法，遗传算法具有优化速度快的优点。由于遗传算法容易陷入局部最优解，学者提出了多岛遗传算法。该算法在每个组中进行独立的优化，各个种群相互隔离，有效促进解的多样性，提高了收敛速度和全局搜索能力。故本文采用多岛遗传算法对空心电抗器进行优化。

1）优化目标：将电抗器金属导体用量作为优化的目标。由式（12）推导出导体用量变化率kMass与变量α'、β'、kd、km的关系。

2）约束变量：在多岛遗传算法优化过程中，对α'，β'，kd，km的取值进行约束以满足工程实际且保证优化效率。α'、β'、kd、km约束条件如式（14）所示。

3）约束条件：电抗器最高温升守恒和电感守恒，且损耗不超过初始设计值。

式中kL为电抗器电感变化率。

4.2 优化实现方法

用多岛遗传算法对电抗器进行优化，首先设定变量，设置种群数为60，岛数为5，遗传代数为5，交叉概率为0.9，变异概率为0.02，迭代次数为1 500。根据约束条件产生初始种群，针对优化目标，通过优化算法从中获得最优解，实现该电抗器的优化。优化流程如图21所示。

图21 优化流程图Fig.21 Optimization flow chart

4.3 优化结果

优化变量α'，β'，kd，km在多岛遗传算法中的迭代过程如图22所示。

图22 优化变量的迭代过程Fig.22 The iterative process of optimizing variables

图中结构参数的最优解用红色的空心圆表示。根据以上优化流程，得到电抗器结构参数的最优解如表2所示。

表2 最优结构参数Table 2 Optimal structure parameters

由优化结果可知，通过多岛遗传算法对干式空心电抗器进行全局寻优，使得电抗器在保持电感、最高温升恒定且损耗基本不变的情况下金属导体用量达到最低且为优化前的78.8%。

5 结论

本文将空心电抗器金属导体用量作为优化目标，在保证电感和温升恒定且损耗满足要求的前提下实现电抗器优化，采用多岛遗传算法获得了最佳的设计参数，得到如下结论。

1）根据等高等热流的电抗器设计参数，建立了三维流场-温度场耦合仿真模型，仿真结果表明电抗器内部各包封线圈温升分布和最高温升基本相同，为电抗器热磁联合优化的实现奠定了基础。

2）根据电抗器包封线圈-气道单元散热特性，推导最高温升守恒约束条件；结合电感守恒和结构方程，建立了电抗器金属导体用量、损耗与整体结构尺寸比例、包封数量和气道宽度的关联式。结果表明电抗器金属导体用量最小时，损耗明显增加。

3）将电抗器金属导体用量最小化作为优化目标，采用多岛遗传算法优化，获得了一组结构参数的最优解。结果表明，在满足电抗器电感和温升恒定且损耗达到要求的条件下，优化方法得到结构参数最优解，电抗器金属导体用量为优化前的78.8%。