基于属性隐藏的高效去中心化的移动群智数据共享方案

蒋沥泉，秦志光

(电子科技大学信息与软件工程学院 成都 611731)

随着传感技术、大数据技术以及移动物联网的快速发展，移动群智技术作为一种新型大规模感知技术，能够利用用户随身携带的移动设备突破时间与地点的限制，随时随地地借助云服务平台进行大规模的实时数据感知、传输和共享[1-3]。随着便携式移动设备传感器集成的精细化以及功能的多样化，其应用也越来越广泛，如交通导航、环境监测、医疗服务等[4-5]。尽管移动群智应用能够极大地提升人类生活质量，然而由于在应用过程中涉及大量的数据传输、交换和共享，这使得群智感知的应用也面临着一系列数据隐私和安全问题。如攻击者可以通过非法获取用户上传的群智医疗等敏感信息来推导其健康状况，进而进行一系列恶意造谣和攻击。社交用户传输给应用服务器的群智数据通常带有时空信息（含有收集数据时的位置），攻击者可以非法获取这些数据并可能利用这些数据推导出用户的生活习惯、行为、家庭住址等敏感信息，从而获取用户的隐私并可能对用户发起恶意攻击。因此，在保证数据隐私性的前提下，如何实现对群智数据的授权访问是移动群智应用首要解决的问题[6-8]。

基于属性加密的访问控制技术是一种有效的解决方法[9-10]。在该技术中，用户的私钥和一组属性集（或一个访问控制）绑定在一起，加密的数据和访问控制（或一组属性集）绑定在一起。当用户私钥中的属性集（访问控制）和密文中的访问控制（属性集）相匹配时，该用户才有权访问数据。然而，在现有的大多数基于属性加密的访问控制中，用户的密钥通常是由一个中央权威去生成和分配，这就需要该权威机构是完全可信的。而在现实的应用场景中，中央权威机构由于托管着用户所有的密钥，可能伪装成合法用户去访问用户的数据，使得用户数据隐私性遭到破坏。因此，如何实现去中心化和分布式的访问控制减少中央权威的信任成为亟待解决的挑战。此外，现有的大多数基于属性的访问控制方案中都过于专注用户数据机密性的保护，很少考虑用户属性的隐私性。如在移动群智的医疗服务场景中，群智用户选择一个访问控制，如“人民医院”“精神科医生”“生理医生”“心理医生”，对自己的群智医疗数据进行加密，使得只有人民医院的精神科医生、生理医生或心理医生才能访问其医疗数据。然而，由于密文中的访问控制是以明文的形式附加在密文数据上的，这就使得任何非法用户即使不能解密其密文数据，也能通过访问控制大致推测该用户可能患有生理或心理疾病，这无疑在一定程度上损害了用户的隐私。因此，如何防止访问控制的隐私性泄漏也成为另一个待解决的挑战之一。除了实现去中心化和分布式的访问控制以及保证访问控制的隐私性之外，考虑到大多数的基于属性加密的方案其密文长度过长、解密效率过低，这对于资源受限的移动群智用户难以快速地解密并访问数据，因此，如何保证资源有限的群智用户能以最少的耗能快速实现对目标数据的访问也是一个现实的挑战。

目前来说，大多数基于属性的加密方案都只能部分解决以上挑战。如具有去中心化功能的基于属性的加密方案[11-18]仅能够实现中心化和分布式的访问控制，无法实现对访问控制的隐私保护和高效的数据访问。具有策略隐藏功能的基于属性的加密方案[19-25]仅能够实现对访问控制的隐私保护，无法实现去中心化和高效的数据访问；具有外包功能的基于属性的加密方案[26-33]仅能够实现高效的数据访问，而没有考虑去中心化和访问控制的隐私保护；此外，还有一些具有隐私保护的去中心化功能的基于属性的加密方案或基于外包的具有隐私保护的属性基加密方案要么没有考虑用户解密效率，要么未考虑去中心化问题[14,25,34-35]。

为了实现移动群智应用场景下的属性隐藏、去中心化以及高效的数据访问，本文提出了一个基于属性隐藏的高效去中心化的移动群智数据共享方案。本文的主要贡献如下。

1）细粒度访问控制：本方案允许群智用户指定基于属性的访问控制用于加密群智数据，使得只有满足访问控制的用户才能访问该群智数据。与之前的细粒度访问控制相比，本方案的访问控制更高效。

2）权威去中心化：本方案允许多个权威机构为群智用户共同生成私钥，使得单独的权威机构无法伪装成合法的用户非法访问目标数据。相较于之前中心化的属性权威的问题，本方案能够防止抗权威密钥泄漏。

3）属性隐藏： 本方案支持对访问控制的隐私保护，本质上来说访问控制是一组属性的描述，实现对访问控制的隐私保护等同于实现对用户属性的隐藏。与之前的访问控制方案相比，本方案考虑了访问控制的属性隐私。

4）外包解密： 本方案允许群智用户能够以最低的能耗去快速解密和访问目标数据。

1 理论知识

1.1 困难性问题

n-线性假设：给定一个群 (p,G1,G2,GT,e)，不存在一个多项式区分者可以以不可忽略的优势区分，这里， γ是 从Zp选 取长度为n的 随机矩阵，Z是 从Zp选取n+1行1列 的随机矩阵，R为 从Zp选 取n+1行n列的随机整数矩阵。

1.2 系统模型

在图1 所示的本系统模型中，涉及4 种不同类型的实体: 权威机构、云服务器、数据拥有者、数据发送者。具体来说，首先权威机构生成系统公开参数，并向系统中的所有实体公开。此外，所有的权威机构为用户生成私钥，并将生产的私钥发送给用户。数据拥有者通过加密算法将其群智数据加密生成密文，并将生成的密文发送到云服务器上存储和共享。当数据使用者想访问存储在云服务器上的密文数据，他首先盲化其私钥生成盲化密钥和转换密钥，然后将盲化密钥发送给云服务器。云服务器在接收到盲化密钥时，执行外包解密操作，并将转换后的外包密文发送给该数据使用者。数据使用者在接收到转换的外包密文后，使用转换密钥恢复明文信息。

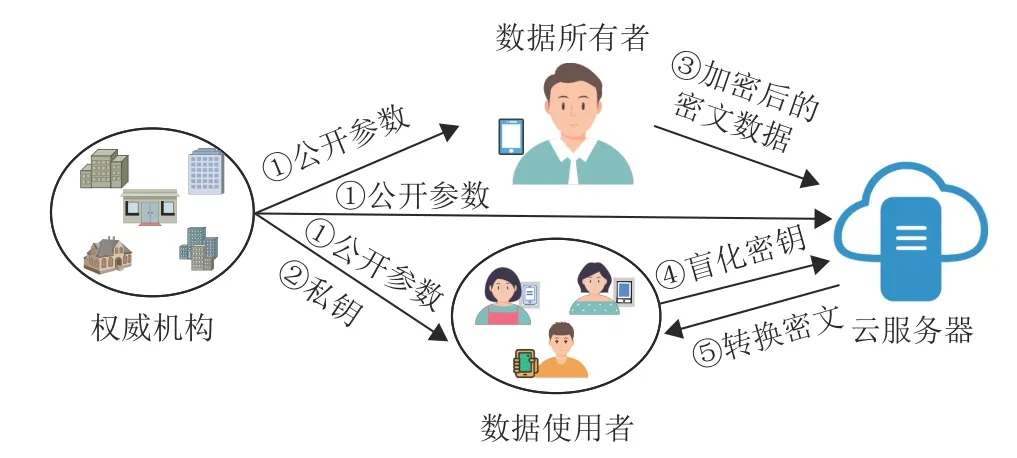
图1 系统模型图

和其他类似方案的安全模型定义相同[14-15,18]，本方案中所有的权威机构都是半可信的第三方，即诚实好奇的第三方，它们能忠实地执行公钥生成和发布，为用户生成其各自的私钥，但可能伪装成合法用户非法访问数据。云服务器是半可信的，即为用户提供无限的存储资源以及为用户忠实地执行其指示的操作，但也很好奇地试图去了解其存储的数据或执行的解密内容。数据拥有者是诚实的数据发送方，主要负责上传数据，以分享给其他用户实现非交互式的数据访问。数据访问者是不可信的数据访问方，即非授权用户试图通过发起包含合谋攻击等手段以获取合法权限，从而达到其非法访问非授权用户数据的目的。

1.3 形式化定义

本方案由如下若干个算法组成。

SETUP(λ): 输入安全参数 λ ， 输出公共参数 pp，该算法由所有权威机构执行。

AuthSetup(pp,i): 输入公共参数 pp、 权威机构索引i，生成其公私钥 PKi和 SKi，该算法由权威机构执行。

Encrypt(pp, PKi,x,m): 输入公共参数 pp、公钥PKi、 访问控制向量x、 加密消息m，该加密算法输出密文 CT ，该算法由数据所有者执行。

KeyGen(pp, SKi, PKi, GID,z) : 输入公共参数 pp，所有权威机构私钥 SKi、 所有权威机构的公钥 PKi、用户的全局身份 GID、 属性向量z，该密钥生成算法为用户生成私钥U Ki，该算法由各权威机构执行。

KeyGenout(pp, UKi): 输入公共参数 pp、用户私钥 UKi，该密钥盲化算法为用户生成盲化私钥(z′,UK′i)和 转换密钥 tk ，该算法由数据使用者执行。

Decryptout(pp, CT, (z′, UK′i)): 输 入 公 共 参 数pp、 密文 CT、 盲化私钥 (z′,UK′i)，该外包解密算法生成外包密文 CT′，该算法由云服务器执行。

Decrypt(pp, CT′, tk): 输入公共参数 pp、 外包解密密文 CT′、 转换私钥 tk，该解密算法输出明文消息m，该算法由数据使用者执行。

1.4 安全游戏

定义1 对所有攻击者 A来说，若能以可忽略的优势赢得与挑战者 C之间的游戏，那么本方案能够实现语义安全性，即明文的机密性。

参数建立阶段 (Setup) ：挑战者 C执行Setup(λ)和AuthSetuppp,i算法生成公共参数pp和权威机构的公共参数 PKi， 并将其发给攻击者 A。

密钥询问阶段 ( Key Query)： 攻击者 A 发送对于属性向量z的密钥请求，挑战者 C 执 行KeyGen(pp,SKi, PKi, GID,z)为 攻击者生成如下密钥 UKi,GID,z。注意在此阶段，允许攻击者获取部分 U Ki,GID,z，且在获得密钥后允许执行 K eyGenout(pp, UKi)进行密钥盲化。

密文生成阶段 ( Ciphertext) ： 攻击者 A 选择两个等长的消息mc,c∈{0, 1}以 及发送访问向量x0、x1，挑战者 C 执行E ncrypt(pp, PKi,x,m)生 成C Tc。

猜测阶段 Guess： 攻击者 A输出一个对消息mc的 猜测比特c′， 若c=c′， 则攻击者 A赢得该游戏。

2 基本构造方案

SETUP(λ)：该算法由共同权威机构执行。输入安全参数 λ，该算法首先选取一个双线性群BG=(p,G1,G2,GT,e)， 其 中，g1，g2分 别 表示 群G1和G2的 一个生成元。随后，该算法随机从Zp选取一 个n+1行n列 的 矩 阵，一 个n+1行n+1列 的矩阵。其次，选取n+2个哈希函数H,H1,···,Hn+1:{0,1}*→Zp。最后，该算法生成公共参数

AuthSetup(pp,i)：该算法由每个权威机构生成各自的公私钥。输入公共参数 pp、权威机构索引i，该算法首先从Zp选 取一个n+1行n+1列的矩阵、一 个n+1维 向 量 αi∈Zp、一 个 数βi，生成和存储其私钥 SKi=(Si, αi, βi)，并公开其公钥

3 正确性和安全性分析

3.1 正确性分析

当用户的属性向量和访问向量正相交时，即〈x,z〉=0表示用户的属性集合满足密文中的访问控制，则以上等式，其中，随后，用户可以正确恢复消息m=C′/Atˆ。

3.2 安全性分析

为了能够证明本方案的语义安全性，定义了一系列的游戏G ame如下。

Game0：该游戏与定义1 中一样，模拟的是方案真实的安全游戏。

Game1：该游戏除了随机预言机回答的询问不一样外，其他均与游戏 G ame0和一样。具体来说随机预言机模拟的过程如下：挑战者 C从Zp中随机选取一个长度为n的 向量r，计算h=Br，然后存储h的值去回答攻击者的随机预言机询问。

Game4： 该游戏几乎与游戏 Game3一样，除了加密消息时随机选取的群中的元素。

Game5： 该游戏几乎与游戏 Game4一样，除了选取的访问向量x被一个随机向量x*取代。注意该游戏从攻击者 A的角度无法区分加密的消息，因此无法以一定的优势赢得该游戏。

引理 1 游戏G ame0和 游戏G ame1的不可区分性

如果存在一个攻击者 A能够区分游戏 Game0和游戏 Game1， 那么就存在一个挑战者 C能够以不可忽略的优势解决线性判定性问题 （decisional linear problem）。

当h∈Span(B)h∈Span(B)时，密钥和随机预言机响应的分布与游戏 G ame1完全相同，而在另一种情况下，其分布与游戏 Game0完 全相同。通过k-判定性线性问题，可以得知攻击者 A只能够以可忽略的优势区分这两个游戏。

引理 2 游戏 Game2,j-1,3和 游戏 Game2,j,1的不可区分性

如果存在一个攻击者 A 能够区分游戏Game2,j-1,3和 游戏 G ame2,j,1，那么就存在一个挑战者C能够以不可忽略的优势解决线性判定性问题。

参数建立阶段 ( Setup) ：挑战者 C 如实际方案中一样随机选择一个长度为n+1的 向量 αi∈Zp、一个随机数tˆ ∈Zp、 随机矩阵R，a⊥，Si，V，生成公开参数以及权威机构的公钥，。

密钥询问阶段( Key,Query) ：输入第m个密钥询问，挑战者 C为攻击者生成如下密钥：

式中，r表示从Zp中选取的随机值组成的一个长度为n的向量。注意攻击者在拿到密钥后可以进行密钥盲化，模拟外包的过程。

密文生成阶段( Ciphertext) ： 攻击者 A 选择两个等长的消息mb,b∈{0,1}， 挑战者 C随 机选择一个 γ，计算如下：

当h∈Span(B)时，密钥和随机预言机响应的分布与游戏 Game2,j-1,3完全相同，而在另一种情况下，其分布与游戏 Game2,j,1完 全相同。通过k-判定性线性问题，可以得知攻击者 A只能够以可忽略的优势区分这两个游戏。

引理 3 游戏G ame2,j,1和 游戏G ame2,j,2不可区分性

如果存在一个攻击者 A能够区分游戏Game2,j,1和游戏 Game2,j,2， 那么就存在一个挑战者 C 能够以不可忽略的优势解决线性判定性问题。

以第j个密钥，其中tˆ是由挑战者C从Zp中 随机采样的。在第j个密钥询问中，攻击者A向挑战者 C 发送有关密钥的属性向量z，挑战者C执行如下操作：

从以上可以看出Si和的分布显然是相同的。此外，还可以得知若密文和权威机构的公钥是使用而 不是Si生成的，则二者没有区别。具体来说，对于公钥的生成如下：

对于密文生成如下：

式中，h=Br+(t/n)a⊥；r∈；t∈Zp。可以得到

因此，用户私钥可以得到:

这样可以轻易得知游戏G ame2,j,2的精确分布。

引理 4 游戏G ame2,j,2和 游戏G ame2,j,3的不可区分性

如果存在一个攻击者 A能够区分游戏Game2,j,2和游戏 Game2,j,3， 那么就存在一个挑战者 C能够以不可忽略的优势解决k-线性判定性问题（decisional linear problem）。

参数建立阶段( Setup)：挑战者 C如实际方案中一样随机选择一个长度为n+1的 向量 αi∈Zp，一个随机数t∈Zp， 随机矩阵R，a⊥，Si，V，生成公开参数以及权威机构的公钥。

密钥询问阶段 (Key,Query) ：输入第m个密钥询问，挑战者 C为攻击者生成如下密钥：

式中，r表示从Zp中选取的随机值组成的一个长度为n的向量。注意攻击者在拿到密钥后可以进行密钥盲化，模拟外包的过程。

密文生成阶段 ( Ciphertext) ： 攻击者 A 选择两个等长的消息mb,b∈{0,1}， 挑战(者 C 随 机)选择一个 γ，计算如下：

当h∈Span(B)时，密钥和随机预言机响应的分布与游戏 Game2,j-1,3完全相同，而在另一种情况下，其分布与游戏 Game2,j,2完 全相同。通过k-判定性线性问题，可以得知攻击者 A只能够以可忽略的优势区分这两个游戏。

引理 5 游戏 Game2,q,3和 游戏 Game3的不可区分性

如果存在一个攻击者 A能够区分游戏Game2,q,3和游戏 Game3， 那么就存在一个挑战者 C能够以不可忽略的优势解决线性判定性问题。

当a∈Span(R)时，密钥和随机预言机响应的分布与游戏Game3完全相同，而在另一种情况下，其分布与游戏 Game2,q,3完 全相同。通过k-判定性线性问题，可以得知攻击者 A只能够以可忽略的优势区分这两个游戏。

引理 6 游戏 Game3和 游戏 Game4的不可区分性

如果存在一个攻击者 A能够区分游戏 Game3和游戏 Game4， 那么就存在一个挑战者 C 能够以不可忽略的优势解决线性判定性问题。

证明：挑战者 C随机化选取一个矩阵R，a⊥，使得RT a⊥=0 ， 一个从Zp中选取的随机值组成的一个长度为n+1随机向量 α，一个从Zp中选取的随机数sˆ 。随后，挑战者 C 计 算α ˆ=α-a⊥sˆ。

参数建立阶段 ( Setup) ：挑战者 C如实际方案中一样生成公开参数以及权威机构的公钥

密钥询问阶段 Key,Query: 挑战者 C 为攻击者生成如下密钥:

注意在此阶段，攻击者在拿到密钥后可以进行密钥盲化，模拟外包的过程。

密文生成阶段 ( Ciphertext) ： 攻击者 A 选择两个等长的消息mc,c∈{0,1}， 挑战者 C 随机选择一个向量 γ，一 个 随 机 数 γˆ ，令随后计算由以上公式可以得知元素m′很大概率是群中的一个随机值。那么，密文可以被计算如下：

很容易可以得知游戏 Game3被准确模拟出来，攻击者 A只能够以可忽略的优势区分这两个游戏。

引理 7 游戏 Game4和 游戏 Game5的不可区分性

如果存在一个攻击者 A能够区分游戏 Game4和游戏 Game5， 那么就存在一个挑战者 C能够以不可忽略的优势解决线性判定性问题。

证明：挑战者 C 可以生成如下密文：

属性隐私：攻击者很容易从密文中获取访问控制属性的隐私，这是因为对于基于属性相关的密码体制来说，访问控制通常以明文的形式附贴在密文上。在本方案中，将属性和访问控制转化成属性和访问向量，这两种向量分别用于私钥和密文的生成。在密文生成过程中，访问向量不必以明文的形式附贴在密文上，而是隐藏在密文中，从而避免了攻击者从密文中获取访问控制属性的隐私的可能。

4 性能分析

4.1 功能分析

从表1 可以得知，文献[11]仅支持细粒度访问控制，而不支持权威去中心化、访问控制的属性隐私保护和高效的数据访问；文献[12-13, 16-17, 19]支持细粒度访问控制和权威去中心化，而不支持访问控制的属性隐私保护和高效的数据访问；文献[14, 15, 35]支持细粒度访问控制、权威去中心化、访问控制的属性隐私保护，但不支持高效的数据访问；文献[18]支持细粒度访问控制、权威去中心化、高效的数据访问，但不支持访问控制的属性隐私保护；本方案支持细粒度访问控制、权威去中心化、访问控制的属性隐私保护和高效的数据访问。

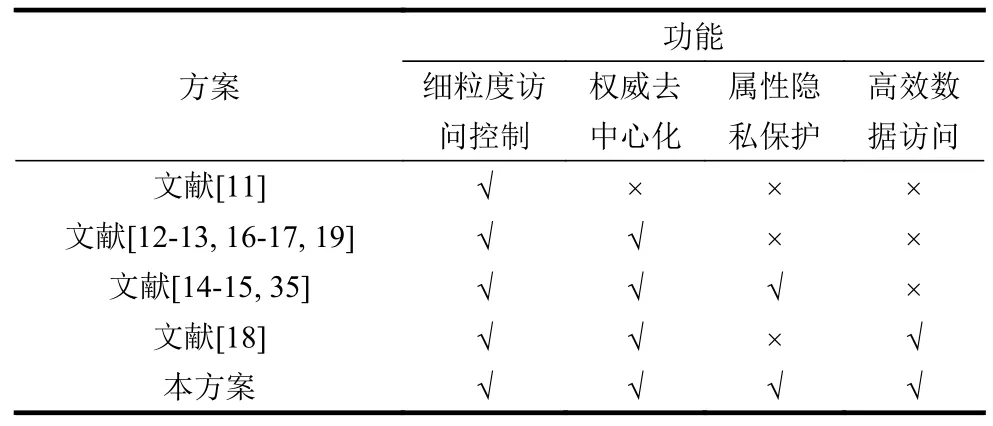
表1 基于多权威的属性基的方案对比

4.2 计算和存储开销理论分析

由于文献[14, 15, 35]与本方案大部分的功能实现相类似，因此本部分仅将文献[14, 15, 35]与本方案进行理论开销对比分析。表2 展示了多权威去中心化属性隐藏的属性基方案的各算法计算开销对比。m，n分别代表权威机构的个数和用户属性的个数；e0，e1分 别表示在群G1，GT中一个指数运算的执行时间，p指的是一个对运算的执行时间。|G1|和|GT|分 别代表G1和GT中元素的长度。

表2 相关方案各算法计算开销对比

从表2 可以得知，在以上所有多权威去中心化属性隐藏的属性基方案中，每一个权威机构参数建立算（AuthSetup）的计算开销都与系统中用户的属性个数相关；用户私钥生成算法（KeyGen）的计算开销与用户属性的个数和权威机构的个数有关；加密算法（Encryption）的计算开销与权威机构个数和属性个数都相关；在解密算法（Decryption）的计算开销方面，只有本方案能够实现高效的解密，即其开销与用户的属性个数和权威机构的个数无关。此外，可以很明显观察到在密钥生成和解密方面，本方案相较于其他方案计算开销最低。

从表3 中可以得知，在以上方案中，存储权威机构生成的公开参数开销与属性个数和权威机构的个数呈正相关；存储用户私钥的开销同样与属性个数和权威机构的个数相关；文献[14-15, 35]存储密文的开销与属性个数和权威机构的个数相关，而本方案的密文存储开销仅与属性个数相关。此外，很容易从表3 观察到本方案用户私钥和密文的存储开销相较于其他方案的存储较低。

表3 相关方案参数存储开销对比

综上所述，本方案在密钥生成和解密的计算开销相较于其他两个方案明显较低。在存储用户私钥和密文的开销方面，本方案相较于其他方案同样明显较低。

4.3 实验分析

由于本方案使用基于属性向量和访问向量来实现策略隐藏，而文献[14-15]方案都是基于线性秘密共享矩阵或访问树的访问结构实现访问策略隐藏。通过以上理论分析可以发现，本方案在计算效率和存储效率存在一定的优势。因此，本部分主要对属性个数和权威机构个数对本方案的各算法计算性能进行评估。本方案在64 bit 的Ubuntu 118.04.6 LTS版本中安装python 3.5 的运行环境，使用的是Charm-Crypto 0.43 的PBC 安装包[35]，本实验是基于512位基本字段的对称曲线SS512。电脑硬件的配置如下: Intel Core i9-9900K CPU@3.60GHz*16，Graphics:GetForce RTX 2 070 Super/PCIe/SSE2，32 GB 内存。

图2 表示的是当权威机构的个数固定为5 时，本方案中相应算法运算时间随着属性向量的长度的变化。图3 表示的是属性向量的长度固定为5 时，本方案中相应算法运算时间随着权威机构的个数的变化。从图2 中可以看出，当权威机构的个数固定时，本方案的AuthSetup，Encryption 和KeyGen 算法的计算时间随着属性向量的长度呈线性关系，而Decryption 算法的计算时间与属性向量的长度无关。

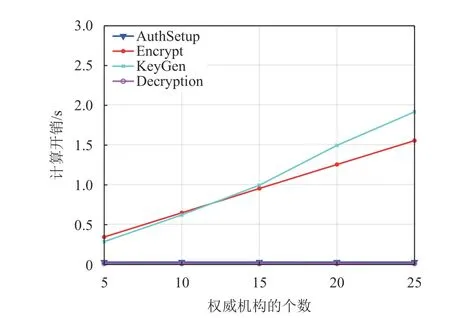
图3 各算法随权威机构个数变化的计算开销

从图3 中可以看出，当属性向量的长度固定时，本方案的Encryption 和KeyGen 算法的计算时间随着权威机构的个数呈线性关系，而AuthSetup和Decryption 算法的计算时间与属性向量的长度无关。

综上所知，本方案的解密计算开销基本保持恒定，表明本方案能够使移动用户在资源受限的条件下依然可以高效访问密文数据。

5 结 束 语

本文针对移动群智场景中数据共享过程存在安全、隐私和效率的问题，提出了一个基于属性隐藏的高效去中心化的移动群智数据共享方案。本方案能够实现细粒度的授权访问、访问控制的隐私保护、权威去中心化以及高效数据访问。并通过严格的安全性分析和性能分析，证明了本方案在应用到移动群智数据共享场景中的安全性、高效性和可行性。本方案访问控制的表达性较弱，即仅支持与门的访问控制的向量转化。未来工作将基于本方案进行扩展，设计出支持可搜索、可撤销的方案。