基于变参数超混沌系统的多图像加密方法

罗 敏，何雨莲，李宜磊，张怀武，文岐业

(电子科技大学电子科学与工程学院 成都 611731)

随着数字通信技术的飞速发展，数字图像以其易于获取、处理和存储的优势，成为人们传递信息和感知世界的重要方式，广泛应用于工业、医药、军事、航天等各个领域。与此同时，伴随而来的则是严重的安全隐患，包括未经授权地传播、复制、篡改及伪造等。因此，如何保护数字图像内容的安全成了亟待解决的问题。

目前图像加密主要采用基于混沌系统的图像加密技术[1-4]，简称混沌图像加密方法，主要包括图像置乱[5-7]与图像扩散[8-10]两种方法。图像置乱方法通过改变图像像素的位置来改变原始图像，使得肉眼无法直观地辨认明文图像，以此达到图像加密的目的。置乱方法主要包括Arnold 变换[11]、Baker 变换[12]与幻方变换[13]这 3 种。图像扩散方法对图像中的像素及其相邻像素进行异或操作，再用变换后的像素替换原始像素，即打乱原始图像的像素值，以此达到图像加密的目的。混沌系统用于对置乱和扩散提供索引矩阵，常用的混沌系统有Logistic 混沌映射[14]、Chebychev 映射[15]、Lorenz 混沌系统[16-17]、Chen 混沌系统[18]等。

与传统图像加密方法相比，混沌图像加密方法具有密钥空间大、加密速度快等优点。然而，当前混沌图像加密方法依然存在诸多问题亟待解决。具体为：1）普遍采用低维及参数固定的混沌系统，所设计的密钥系统的密钥空间不够大、复杂度较低，在计算机有限精度下，容易出现短周期现象及混沌退化，容易受到攻击者使用相空间重构方法进行的攻击破译；2）仅采用简单的像素置乱及像素扩散方法，如基于位置变换的置乱方法、基于异或运算的扩散方法，它们的复杂度较低、易于破译，即仅仅对图像进行简单的像素位置和大小上的变换；3）每一幅图像都使用相同的密钥流，安全性较差，攻击者只要破译一幅图像就可以对其他密文图像进行破译，未有效地将密钥与明文图像进行联系。

1 算法设计

为了解决图像加密方法的上述问题，提供了一种基于变参数超混沌系统与S 形扩散的多图像加密方法，如图1 所示。首先借助Alpha 通道的概念，将输入灰度图像（原始图像）进行重构，然后将其作为初始信息输入SHA-512 算法生成初始密钥，再利用变参数超混沌系统迭代生成的5 组混沌序列对明文图像进行幻方变换，实现像素位置的变换，最后基于S 形扩散实现像素数值的变换，从而得到密文图像。具体技术方案包括以下3 个步骤。

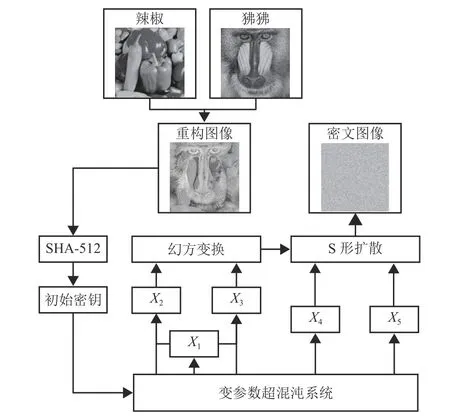
图1 多图像加密方法的设计框架

1）首先对输入灰度图像对进行图像预处理，得到重构GA 图像P，并将其像素序列作为初始信息输入SHA-512 哈希函数生成初始密钥流；

2）再将初始密钥流作为初始值，输入变参数超混沌系统迭代生成混沌序列X1、X2、X3、X4与X5，并基于混沌序列X1、X2、X3计算得到索引序列；再根据索引序列对重构GA 图像P采用幻方变换进行置乱，得到置乱后的密文图像C；

3）最后对密文图像C进行顺向S 形扩散得到顺向扩散后矩阵，再对顺向扩散后矩阵进行逆向S 形扩散，得到最终密文图像T。

1.1 变参数超混沌系统

根据Fan 超混沌系统的定义[19]，其数学模型如式(1)所示，其典型特征是：当a=30、b=10、c=15.7、d=5、e=2.5、f=4.45、g=38.5 时，该混沌系统存在两个正的Lyapunov 指数，即存在复杂的混沌行为。

式中，x1、x2、x3、x4、x5为系统变量；a、b、c、d、e、f、g为系统参数；x˙1、x˙2、x˙3、x˙4、x˙5为每次迭代产生的新系统变量（Lyapunov 指数）。

为了增强混沌系统的复杂性和随机性，采用Logistic 混沌映射作为扰动系统，对Fan 超混沌系统的参数施加扰动来构造变参数混沌系统，以生成具有更高随机性的混沌序列，Logistic 映射为非线性的迭代方程，如式(2)所示，其典型特征是：当满足3.57<µ<4 时，Logistic 映射工作于混沌状态，即为Logistic 混沌映射。

式中，y为系统变量；µ为系统参数；y˙为每次迭代产生的新系统变量。

引入参数扰动项后的变参数超混沌系统的数学模型如式(3)所示，根据混沌系统的定义，无论初始值如何变化，系统变量都会回到一个固定的吸引域，由于式(1)、(2)均为混沌系统方程，因此Lyapunov 指数的数值经过式(3)多次迭代后，只跟扰动强度λ 有关，与y、xi(i=1,2,···,5)的初始值无关，y、xi的初始值可取实数范围内的任意值，最终稳定的Lyapunov 指数的数值只依赖于扰动强度λ。

式中，x1、x2、x3、x4、x5为系统变量；a、b、c、d、e、f、g为系统参数；x˙1、x˙2、x˙3、x˙4、x˙5为每次迭代产生的新系统变量；λ 为扰动强度参数；y为Logistic 混沌映射的系统参数。

为了确定扰动强度参数λ 的取值范围，确保变参数超混沌系统始终处于混沌状态，对变参数超混沌系统的Lyapunov 指数和系统相图进行仿真分析，在系统参数a=30、b=10、c=15.7、d=5、e=2.5、f=4.45、g=38.5、µ=3.8 时，取y=1、xi=0.1 作为初始值，当变参数超混沌系统自身迭代300 次后，Lyapunov 指数的数值趋于稳定，将第301 次迭代产生的y、xi以及系统参数代入式(3)，得到了变参数超混沌系统（λ 在-5～4 之间变化）的Lyapunov指数变化曲线，如图2 所示。当扰动强度参数λ 在-4.0～2.35 之间时，x1(λ)和x2(λ)始终大于零，即始终存在两个正的Lyapunov 指数，使变参数超混沌系统保持混沌状态。图3 给出了扰动强度参数λ 为0 时，变参数超混沌系统的系统相图，通过系统相图能够更直观地表现出变参数超混沌系统的动力学行为。

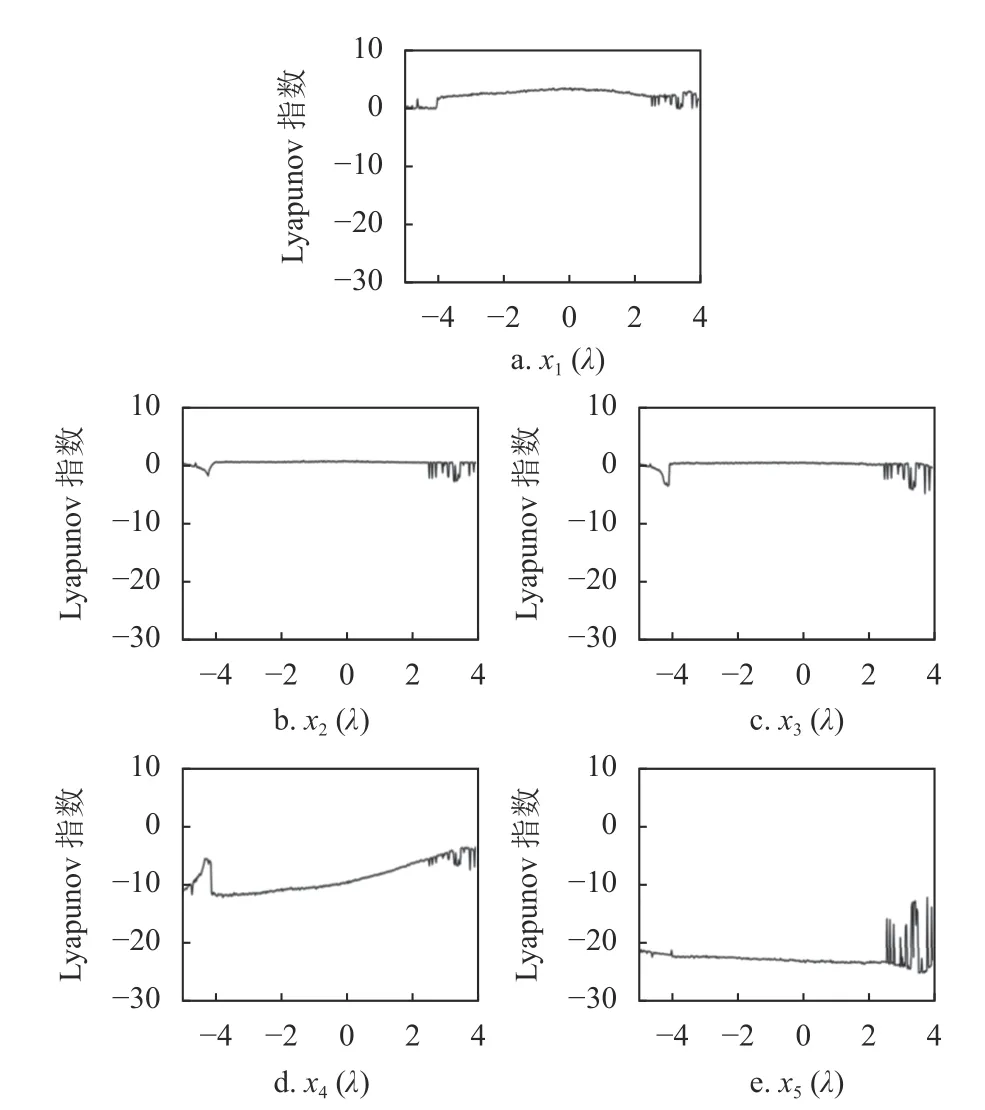
图2 变参数超混沌系统的Lyapunov 指数变化曲线

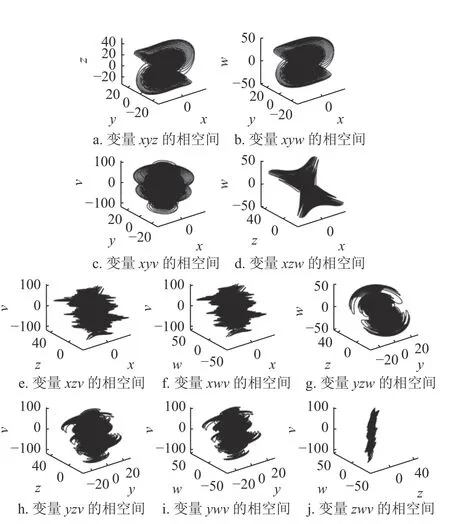
图3 变参数超混沌系统的系统相图

1.2 多图像加密方法

多图像加密方法的流程图如图4 所示，包括图像预处理与密钥生成、置乱阶段和扩散阶段3 个步骤。以下使用如图5 所示的传统图像辣椒（灰度图像P0）与狒狒（灰度图像P1）为例进行说明，两张图像的像素大小均为512×512，记为M×N，M为图像像素长度、N为图像像素宽度。

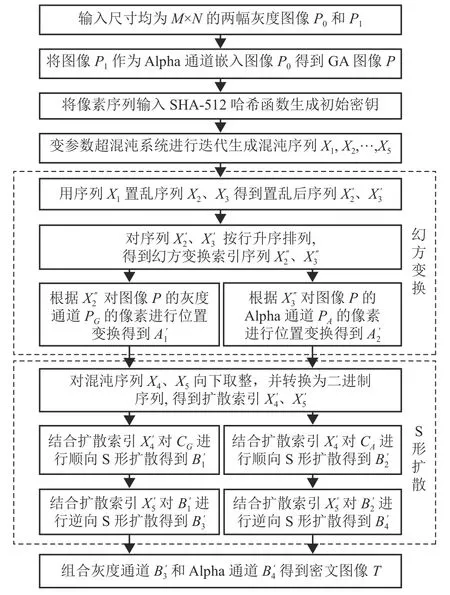
图4 多图像加密方法的流程图

图5 原始图像

1.2.1 图像预处理及密钥生成

1）引入Alpha 通道的概念，将灰度图像P1作为Alpha 通道嵌入至灰度图像P0，进而形成一幅具有不同透明度的Grayscale-Alpha(GA)图像P；

2）将图像P分解为灰度通道PG与Alpha 通道PA两路数据矩阵（矩阵大小均为M×N），再将灰度通道PG与Alpha 通道PA转换为一维矩阵，并拼接构成一维矩阵PC，将一维矩阵PC作为初始信息，输入SHA-512 哈希函数，生成512 bit 的二进制哈希值，具体运算为：

式中，reshape( )表示将指定矩阵变换为特定行列数的矩阵。

3）将二进制的哈希值以每8 bit 为一位转化为十进制，进而得到64 位十进制数据ci(i=1,2,···, 64)；

4）对64 位十进制数据进行异或运算得到加密方法所需要的初始密钥流，具体运算为：

需要说明的是：式(5)中λ 的归一化过程能够保证其取值在-4.0～2.35 之间，进而保证变参数混沌系统保持混沌状态。

1.2.2 置乱阶段

1）根据初始密钥流，应用四阶龙格库塔算法对变参数超混沌系统进行迭代，为避免暂态效应的影响，舍弃前500 组数据，从第501 个数据进行截取，最终得到5 组一维混沌序列X1、X2、X3、X4与X5，其中，每组混沌序列的长度均为M×N；

2）将混沌序列X1按行升序排列，得到置乱后矩阵I1与索引序列，具体运算为：

式中，sort( )表示排序函数；‘2’表示按行排序；ascend表示升序排列；

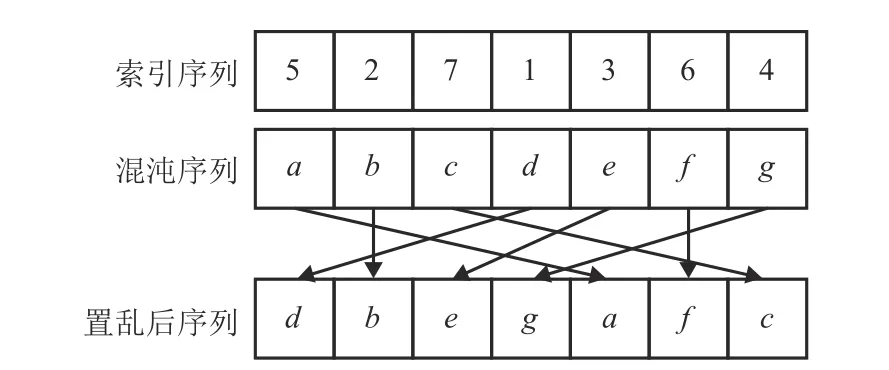
图6 混沌序列置乱示意图

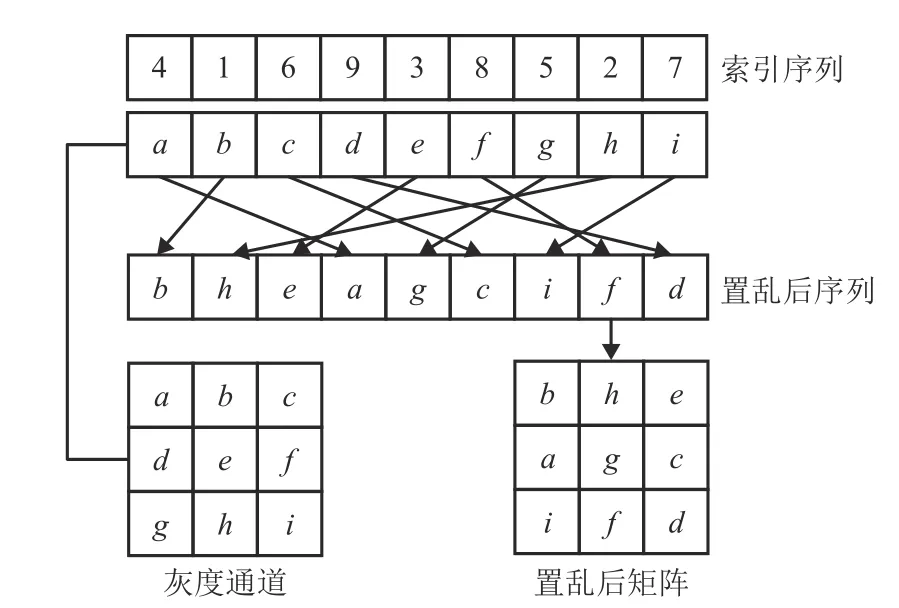
图7 幻方变换示意图

式中，reshape( )表示将指定矩阵变换为特定行列数的矩阵。

1.2.3 扩散阶段

1）将混沌序列X4与X5进行向下取整数运算，得到十进制整数的混沌序列，然后将十进制转换为二进制的一维序列（长度均为M×8N）：

式中，dec2bin( )表示将十进制转换为二进制；floor( )为向下取整函数。

2）将密文图像C分解为灰度通道CG和Alpha通道CA两路数据矩阵（矩阵大小均为M×N），先对灰度通道CG和Alpha 通道CA分别进行顺向S形扩散，再进行十进制到二进制的转换，得到二进制的一维矩阵（长度均为M×8N）；然后根据式(10)进行异或运算，得到二进制的一维矩阵B1与B2（长度均为M×8N），将二进制矩阵B1与B2转换为十进制矩阵，并将一维变换为二维，得到顺向扩散后矩阵（矩阵大小均为M×N）：

式中，mod( )表示取余运算；M、N为输入灰度图像的像素长度和像素宽度；bin2dec( )表示将二进制转换为十进制。

顺向S 形扩散的定义如图8a 所示，具体运算为：

图8 顺向和逆向S 形扩散示意图

式中，Sforward( )表示顺向S形扩散运算；Q为原始矩阵；Q′为顺向S形扩散结果。

逆向S 形扩散的定义如图8b 所示，具体运算为：

式中，Sreverse( )表示逆向S形扩散运算；Q为原始矩阵；Q′′为逆向S形扩散结果。

1.3 多图像解密方法

图像解密方法使用与加密方法相同的密钥，具体包括以下3 个步骤。

1）将密文图像分解为两通道十进制数据矩阵，即灰度通道J与Alpha 通道K（矩阵大小均为M×N），对J与K分别进行顺向S 形扩散的逆操作，再进行十进制到二进制的转换，得到二进制的一维矩阵J′与K′（长度均为M×8N）；根据式(16)进行异或运算，得到二进制的一维矩阵J1和K1（长度均为M×8N），将二进制矩阵J1和K1转换为十进制矩阵，并将其变换为二维矩阵（矩阵大小均为M×N），具体运算如式(17)所示：

2 实验结果与分析

2.1 加解密实验结果

通过上述多图像加解密方法，对如图5 所示的传统图像辣椒与狒狒进行加解密实验，得到的仿真图如图9 所示。由图可见，密文图像是完全无序的，无法分辨出原始图像的任何有效信息。

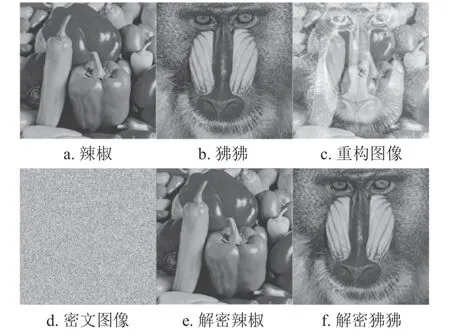
图9 原始图像加解密实验的结果展示图

2.2 算法的性能分析

为了验证多图像加密方法的安全性能，图10给出了加解密前后的直方图；由图可见，图像辣椒与图像狒狒的密文图像直方图均近似均匀分布，攻击者很难从中获取有效信息。

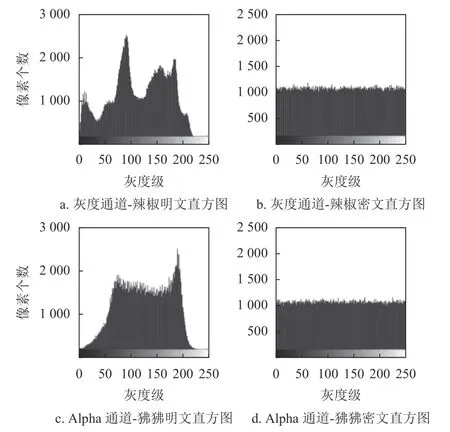
图10 灰度通道和Alpha 通道的明文和密文直方图

此外，为了更加直观地说明多图像加密方法打破相邻像素相关性的能力，图11 给出了加密前后灰度通道与Alpha 通道的像素相关性分布图。由图可见，加密后的相关性分布遍布整个区域，有效地破坏了明文图像的像素相关性分布。

图11 灰度通道和Alpha 通道的明文和密文相邻像素相关性对比图

信息熵用于表征一个数字图像像素的分布情况，信息熵越接近理想值8，像素分布越随机。为验证加密算法扰乱明文图像像素分布的能力，对辣椒和狒狒加密前后图像进行信息熵分析。表1 给出了经加密算法加密后，明文图像与密文图像的信息熵。可以看出，密文图像的信息熵接近理想值8，这证明设计的加密算法可以更加有效地打乱明文像素分布。

表1 信息熵分析表

加密算法的抗差分攻击能力主要体现在对同一明文图像任一像素点施加微小改变，密文图像随之产生相应变化的能力。本文将明文图像某一像素点的像素值减1，然后通过计算NPCR 和UACI，对抗差分攻击能力进行评估，结果如表2 所示。可以看出，加密算法的NPCR 和UACI 接近理想值99.609 4%和33.463 5%，说明设计的加密算法对明文的微小变化具有更高的敏感性，可以更加有效地抵御差分攻击。

表2 抗差分攻击能力分析表 %

当图像进行网络传输时，可能会引入各种噪声干扰，导致密文图像某些像素点的像素值发生改变，进而影响到原始图像有效信息的恢复。本文对辣椒和狒狒加密后的密文图像分别加入5%、10%和20%的椒盐噪声，以此验证加密算法的抗噪声能力。图12 为辣椒和狒狒引入椒盐噪声后的密文图像以及运用解密算法解密后的图像。可以看出，引入不同程度的椒盐噪声后，解密图像虽然受到一定程度的损坏，但是依旧可以分辨出大部分有效信息，因此所提加密算法具有良好的抗噪声能力。

图12 算法性能对比：抗噪声分析

为验证加密算法的抗剪切能力，本文将辣椒和狒狒加密后的密文图像，在不同位置剪切不同像素大小的信息，然后再对其进行解密，剪切后的密文图像以及相应的解密图像如图13 所示。从图中可以看出，密文图像受到人为剪切后，加密算法仍然可以恢复出原始图像的主要信息，具备良好的抗剪切能力。

图13 算法性能对比：抗剪切分析

3 结 束 语

基于变参数超混沌系统的多图像加密方法，主要由4 个部分构成：变参数超混沌系统构建、图像预处理与密钥生成、幻方变换置乱和S 形扩散。首先借助Alpha 通道的概念，将输入灰度图像对进行重构，然后将重构图像作为初始信息输入SHA-512算法生成初始密钥，再将其输入变参数超混沌系统迭代生成5 组混沌序列，进而对重构图像进行幻方变换，实现像素位置的变换，最后基于S 形扩散实现像素数值的变化，从而得到密文图像。

与传统图像加密方法相比，基于变参数超混沌系统的多图像加密方法，具有如下优点：

1）将混沌系统的参数作为加密过程中的控制变量之一，运用另一个混沌系统的状态变量对其施加一定的扰动，以构造变参数超混沌系统，同时确保该混沌系统依旧处于混沌状态，生成具有更高复杂度和随机性的伪随机序列，有效地改善了传统混沌系统的低随机性、低复杂度以及混沌系统退化等缺陷；

2）采用幻方变换的置乱方法，最大程度地对图像像素进行位置上的置乱，并创造性地提出S 形扩散方法，提高了密文图像的无序性，打破了像素相关性分布，具有更优越的加密性能表现，难以被暴力破译；

3）采用SHA-512 算法，结合明文图像生成初始密钥，保证一幅图像仅仅对应一种密钥流，有效地提高了加密算法抵抗明文攻击的能力；

4）本文设计的加密算法可以有效地打乱明文像素分布、有效地抵御差分攻击，具有良好的抗噪声能力和具备良好的抗剪切能力。