影响社团特性的微观结构因素解耦分析

常美琪，肖 婧，许小可

(大连民族大学信息与通信工程学院 辽宁 大连 116600)

社团结构是将网络中的节点组织成多个节点组集合，其中每一节点组集合中的节点间连接紧密或者共享相似的特征或角色[1]。社团结构作为复杂网络中介于微观和宏观特性之间的重要中尺度特性，广泛存在于信息、经济、工程、生物等网络中[2]。如在蛋白质相互作用网络中，社团结构代表了功能相关的蛋白质集合[3]；在社交网络中，社团结构代表了某些相同兴趣爱好的用户集合[4]；在引文网络中，社团结构代表了主题相似的文献集合[5]。社团结构揭示了网络内在隐藏的结构规律和重要动态特性的结构起源，是网络结构和功能间相互作用的重要途径，因此研究社团结构具有重要的理论价值和现实意义。

考虑到社团结构是一种非常重要的中尺度特性，探索社团特性产生的内在原因，尤其是研究网络的微观结构特性，如度分布、匹配系数、聚类系数是如何影响网络社团特性是非常有意义的科学问题。目前研究网络微观特性对社团结构影响的主要方式有两种。一种是将原始网络与其具有某些相似性质的随机化网络的社团结构进行比较，确定社团结构的显著性，从而分析网络社团结构特性是否由某种微观特性衍生[6]，研究发现社团结构可由聚类系数主导生成[7]。另一种是在保持网络平均度或度序列不变的前提下，通过调节网络中匹配系数的大小[8]或三角形模体数量分布[9-10]，观察网络的社团数量或模块度值的变化情况，发现仅在特殊类型网络中匹配系数对社团结构影响明显。相比于匹配系数，网络中三角形结构的数量（聚类系数）变化对社团结构影响更大。

尽管上述研究发现了聚类系数这种微观特性对于社团结构的巨大影响，但目前还存在以下两方面的问题。一方面，在定性上无法确定描述三节点关系的聚类系数是否已经完全解释了各类真实网络社团性质的起源。另一方面，上述研究中没有考虑微观特性间的相互依赖关系，如当改变网络聚类系数时并没有保证网络的匹配系数不变，就直接观察社团结构特性的变化。网络社团结构往往是多种微观性质，如度分布、匹配系数、聚类系数、四节点模体分布（更高阶微观特性）等共同作用的结果，尚无法确定解耦后量化出每一种微观结构对于社团特性贡献程度的具体数值。此外，当前在分析网络微观结构对社团特性影响的研究中，所采用的实证网络数量和类型均较为有限，导致所得的结论是否具有通用性还需要进一步验证。

为了解决以上问题，本文从定性和定量角度出发，基于各类实证网络构建解耦分析网络微观结构对社团特性影响的新框架。为了使研究结果具有鲁棒性、研究结论具有通用性，本文使用了生物、社交、经济、科技、信息网和交通6 大类不同规模的550 个实证网络进行了实验验证。首先，为了揭示表征三节点关系的聚类系数是否已经可以完全解释各类真实网络社团性质的起源，本文基于表征不同阶数微观结构的零模型，并利用统计检验方法完成了真实网络的社团结构显著性检测，实现了不同类型网络微观结构对社团特性影响的定性分析。其次，为了能够量化出各种微观结构对社团特性影响程度，本文提出了基于零模型和中介效应框架的微观结构对社团特性影响的解耦分析方法，量化出各微观结构对社团特性产生的正负影响及贡献程度。

1 社团特性与零模型构造方法简介

1.1 社团结构概念及评价指标

1）社团结构

根据网络中节点间连接的紧密程度将网络划分为一个个“簇”， 将这种“簇”称为网络的社团结构。其中“簇”内的节点之间连接紧密，不同“簇”之间的节点连接较稀疏。

2）评价指标模块度值Q

模块度值Q是近年来常用的一种刻画社团结构强弱的参数，也是一种衡量社团划分质量的标准[13]，它将原始网络与其具有某些相同性质的随机化网络的社团结构进行比较，来度量社团划分质量与社团结构强度，其定义为：

式中，aij是 实证网络的邻接矩阵；ki和kj分别为该网络中节点i和 节点j的度；Ci与Cj分 别为节点i和节点j在网络中所属社团；当两节点属于同一社团，δ取值为1，否则δ 取值为0。Q的取值范围在[0, 1]，一般情况下Q越大，社团划分质量越好，网络的社团结构特性也越强，但当网络规模增大时，由于分辨率限制，其对应模块度值Q也会相应增加。

1.2 零模型构造方法简介

通常把与一个实证网络具有某些相同性质的随机网络称为该实证网络的随机化副本，这类随机化网络在统计学上被称为零模型[11]。一个好的复杂网络零模型能为原始网络提供一个准确的基准，结合统计量指标就可以准确描述出实际复杂网络的非平凡特性[12]。下面是对1—3 阶零模型的构造过程以及与原始网络的共性与差异进行简要描述。

1 阶零模型是在保持原始网络度分布不变的前提下，对原始网络中的边进行随机置乱操作。在微观性质上能保证与原始网络平均度、度序列相同，而匹配系数、聚类系数、更高阶特性不能保证。具体构造过程为：在网络中随机选择两条边断开，随后将这4 个节点间随机连接成两条边，重连边后的4 个节点若能与原始网络4 节点保持相同的度分布，则断边重连成功。否则，撤销先前断边重连操作，再重新选择边完成同样的操作。根据网络的规模与实际需求不断重复上述操作，每次都需保证置乱前后节点度值不变，最终完成1 阶零模型构造。

2 阶零模型是在保持原始网络联合度分布不变的前提下，对原始网络中的边进行随机置乱操作。在微观性质上能保证与原始网络平均度、度分布、匹配系数相同，而聚类系数、更高阶特性没有办法保证。具体构造过程为：在网络中随机选择两条边断开，随后将这4 个节点随机连接成两条边，重连边后的4 节点若能与原始网络4 节点保持相同的度分布与匹配系数，则断边重连成功。否则，撤销先前断边重连操作，再重新选择边完成同样的操作。如果成立则交换边成功，同样根据网络的规模与实际需求不断重复上述操作，每次都需保证置乱前后网络联合度分布不变，最终完成2 阶零模型构造。

3 阶零模型网络是在保持原始网络联合边度分布不变的前提下，对原始网络中的边进行随机置乱操作。在微观性质上能保证与原始网络平均度、度分布、匹配系数、聚类系数相同，而更高阶微观特性没有办法保证。具体构造过程如下：在网络中随机选择两条边断开，随后将这4 个节点间随机连接成两条边，重连边后的4 节点若能与原始网络4 节点保持相同度分布、匹配系数，且重连前后这4 个节点与它们的邻居节点的三角形模体与非三角形的连通三节点模体数量相同，则断边重连成功。否则，撤销先前断边重连操作，再重新选择边完成同样的操作。同样根据网络的规模与实际需求不断重复上述操作，每次都需保证置乱前后网络联合边度分布不变，最终完成3 阶零模型构造。

由上述1—3 阶零模型构造，可以发现随着阶数的增加，断边的约束条件越来越多，原始网络中满足条件可进行随机置乱的边越来越少，构造出来的零模型在结构与微观性质上越来越接近原始网络。

2 微观结构对社团影响的定性分析

利用零模型和统计检验方法对实证网络社团结构特性进行显著性分类，实现不同类型网络微观结构对社团特性影响的定性分析。

2.1 显著性检验方法

在利用原始网络与零模型进行模块度值Q比较来确定原始网络社团结构显著性类型时，需要使用到显著性检验方法，本节使用的显著性检验方法为Z 检验，相关概念描述如下。

Z 检验是一种参数检验方法，它利用标准正态分布理论来判断差异发生概率，从而判断两组值的差异是否明显。在本文中利用Z 检验来完成实际网络与零模型网络模块度值Q差异的显著性检验。Zi(Q)具体公式如下：

式中，Qorigin为 原始网络的模块度值； 为原始网络对应的多个i阶零模型的模块度值的平均值； σQik为 多个i阶零模型的模块度值的标准差；Zi(Q)的 绝对值越大表示原始网络与其i阶零模型网络的社团结构差异越明显。Zi(Q)对 应的Pi值公式定义如下：

式中， ϕ(Zi(Q))为标准正态分布。本文Z 检验显著性判断方法为：当 |Zi(Q)|<1.96 时，Pi>0.05接受原假设，差异不显著；当 |Zi(Q)|≥1.96 时 ，Pi≤0.05拒绝原假设，差异显著。

2.2 基于零模型和“显著性检验”的微观结构对社团特性影响的定性解耦分析框架

本文首先对各类型实证网络进行200 次1—3阶零模型构造，利用社团检测算法对实证网络与零模型进行社团划分得到模块度值Q；然后根据显著性检验方法完成实证网络与其1—3 阶零模型模块度值Q显著性差异的计算，根据结果实现社团结构显著性分类；最后实现微观结构对社团特性影响的定性分析。表1 是根据各阶零模型显著性检验结果对社团结构显著性类型的定义。

表1 社团结构显著性类型定义表

从表1 中可以看出当实证网络G 与其1 阶零模型G1对应的P1>0.05时，G 与G1的社团结构不存在显著性差异，此时称G 不具有社团结构显著性。当实证网络G 与其1 阶零模型G1对应的P1≤0.05， 而与其2 阶零模型G2对应的P2>0.05时，G 与G1社团结构间存在显著性差异，而与G2社团结构不存在显著性差异，此时称G 具有1 阶社团结构显著性。当实证网络G 与其1 阶、2 阶零模型G1、G2对应的P1≤0.05、P2≤0.05，而与其3 阶零模型G3对应的P3>0.05时，G 与G1、G2社团结构间存在显著性差异，而与G3社团结构不存在显著性差异，此时称G 具有2 阶社团结构显著性。同理，当实证网络G 与其1—3 阶零模型模块度Q对 应Pi≤0.05(i∈{1,2,3})都 成 立，G 与G1、G2、G3社团结构都存在显著性差异，此时称实证网络G 具有3 阶社团结构显著性。

本文基于网络社团结构显著性分类实现微观结构对社团特性影响定性分析的解释说明。对于不具有社团结构显著性的实证网络G 而言，G 与其1 阶零模型G1在社团结构上不存在显著性差异，而从微观结构角度来看G 与G1只具有相同的度分布，所以此时度分布即可决定实证网络G 社团结构的产生，只要保证与G 具有相同度序列构造出来的网络即可刻画出与G 非常相近的社团结构。

对于具有1 阶社团结构显著性的实证网络G 而言，因为G 与其1 阶零模型G1在社团结构上存在显著性差异，与其2 阶零模型G2在社团结构上不存在显著性差异，而G 与G1、G2在微观结构上具有相同度分布，与G1不同的是G 与G2在微观结构上还具有相同匹配特性，所以此时可以说度分布并不能刻画实证网络G 的社团结构，但匹配特性可以。

对于具有2 阶社团结构显著性的实证网络G，因为G 与其1 阶、2 阶零模型G1、G2在社团结构上存在显著性差异，与其3 阶零模型G3在社团结构上不存在显著性差异，而G3与G2在微观结构上与原始网络除了具有相同度分布、匹配特性外，其与G 还具有相同聚类特性，所以此时可以说度分布、匹配特性并不能刻画实证网络G 的社团结构，但聚类特性可以。

同理，对于具有3 阶社团结构显著性实证网络G，因为G 与其1—3 阶零模型G1、G2、G3社团结构都存在显著性差异，而从微观结构角度来看G3与G 具有相同度分布、匹配特性、聚类特性，此时度分布、匹配特性、聚类特性都不能刻画其社团结构，需要更高阶微观特性才能刻画出它的社团结构。

上述过程，实现了微观结构对社团特性影响的定性分析。

2.3 实证网络数据及社团检测算法选择说明

本文从CommunityFitNet 数据库[13]中选取了6 大类550 个不同规模的具有代表性的实证网络，进行微观结构对社团特性影响的定性与定量分析研究。其中，包含了124 个社交网络、179 个生物网络、35 个交通网络、70 个科技网络、124 个经济网络、18 个信息网络，涵盖了生活中网络的大部分类型。网络的节点规模在[48, 3 353]范围内，连边规模在[30, 7 562]范围内。

在社团检测算法的选择上，本文选用基于层次聚类的GN 算法，它是一种基于模块度最优化为目标进行自顶向下社团划分的方法。GN 算法基本思想是在初始时将网络中所有节点都归入一个大社团，通过不断切断网络中边介数最大的边，逐步将网络分裂为多个社区，进而获得层次性的社团结构。 GN 算法由于每次迭代都要考虑网络的全局结构，导致时间复杂度较高，只适用于中小型网络的社区划分，但也因为这个原因其社团划分的准确度会比较高。考虑到本文的重点是各类型实证网络与其零模型模块度Q差异的比较，在社团检测算法的选择上主要考虑其能否适用于各种类型的网络，算法的准确度和时间复杂度不是考虑的重点，而GN 算法因其适用的网络类型较广泛所以被选取用于社团划分。此外，使用其他社团检测算法也可以得到本文类似的结论。

2.4 实证结果分析

550 个实证网络社团结构显著性分类的结果如表2 所示，各类型网络中社团结构显著性分布最多的类型加粗标出。

表2 实证网络社团结构显著性检验统计结果

从表2 可以看出，不具有社团结构显著性的网络在各类型网络中数量都非常少，其只占总体网络数量的9.3%。对于这些网络而言，它们的社团结构由度序列即可决定。具有1 阶社团结构显著性的网络数量在各类型网络中更少，其只占总体网络数量的4.5%。对于这些网络而言，它们的社团结构由匹配特性决定。具有2 阶社团结构性显著性的网络数量很多，占总体数量的32.2%，且大多数分布在社交网络中，在124 个社交网络中有118 个具有2 阶社团结构显著性。对于这类网络而言，它们的社团结构可以由网络的聚类系数很好地刻画出来，聚类系数决定了其社团结构的产生。这与文献[7]网络的社团结构可以由3 阶度相关特性有效地刻画（不需要更高阶）的结论是一致的。

同时从表2 中也可以看出在各类型网络中，除社交网络外（如生物、科技、交通、经济、信息网络），具有3 阶社团结构显著性的网络数量是最多的，其占总网络数量的72.2%。对于这类网络而言，聚类系数并不能刻画出它们的社团结构，它们的社团结构需要更高阶的微观特性才可以刻画出来，这和以前研究中的结论是不同的。上述结果也说明，尽管聚类系数特性对于网络社团结构有很强的影响，但并不足以充分揭示除社交网络之外的其他类型网络的社团特性的主要起源。

尽管研究发现网络的社团结构显著性类型不唯一，但无论何种类型网络，度序列和匹配系数对社团结构起决定性作用的数量都非常少。对于大多数社交网络来说，它们的社团结构由3 阶度相关特性（聚类系数）决定，无须更高阶的微观特性。对于其他类型网络（如生物、科技、交通、经济、信息网络）来说，它们社团结构大多数并不能由3 阶度相关特性决定，而由更高阶的微观特性才能决定。

3 微观结构对社团影响的量化分析

基于零模型和中介效应分析框架可分辨出社团结构特性是否是由某种微观结构贡献，并判断和量化出这一因素作为中介变量对社团特性的贡献是正向的还是负向的以及贡献程度的大小，从而实现微观结构对社团特性影响的解耦量化分析。

3.1 中介效应分析

中介效应分析是一个以“因果路径”概念为中心的统计框架。在分析某一变量X对变量Y产生影响的过程中，如果变量X是通过第三个变量Z来影响变量Y，那此时第三个变量Z就是中介变量，中介变量Z在变量X和变量Y间所发挥的作用（促进/抑制）称为中介效应。中介效应分析是检验变量Z是否成为中介变量，作为中介变量发挥何种中介作用以及中介程度有多大的重要步骤。

图1 是对单中介模型的简要介绍。在图1a 表示自变量X对因变量Y的直接作用，在这里不涉及第三个变量，路径系数c1代表自变量X作用于因变量Y的总效应。图1b 表示有中介变量M参与的自变量X对因变量Y的间接作用，其中系数a代表自变量X作用于中介变量M的效应，系数b代表中介变量M作用于因变量Y的效应，两者构成自变量X和因变量Y间的间接效应。系数c2为考虑在控制中介变量后，自变量X作用于因变量Y的直接效应。那么c1=ab+c2，中介效应分析就是检验ab效应是否存在，以及度量出ab效应在总效应中的占比，体现中介效应作用程度的方法。

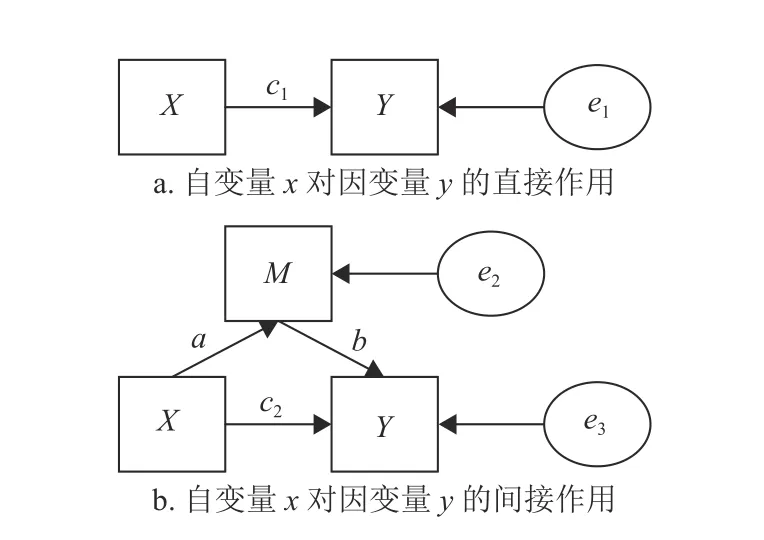
图1 单中介模型图

3.2 基于零模型和中介效应分析的微观结构对社团特性影响的量化解耦分析框架

从微观结构对社团特性影响定性分析中我们发现随着零模型阶数的增加在微观性质上与原始网络越来越相似，模块度值Q（社团结构）也越接近实证网络，由此看出微观结构作为中介变量对网络社团特性起正向的贡献作用，也就是说微观结构对社团特性的强弱起促进作用，接下来对这种促进作用进行量化。

本文通过构造实证网络的1—3 阶零模型，计算实证网络与零模型网络、零模型网络与零模型网络间模块度值差异的方式，依次剔除网络微观特性（高阶特性、聚类系数、匹配系数）对社团结构贡献，实现各社团结构显著性类型的多种类型网络的微观特性（高阶特性、聚类特性、匹配特性）对其社团结构产生贡献程度的量化。

本文主要分析了匹配系数、聚类系数，以及更高阶微观特性对社团结构影响，没有考虑度序列对社团结构的贡献，主要原因是度量实证网络社团结构强弱的主要指标是模块度值。在计算模块度值时，主要是将原始网络与其对应一阶随机化网络的社团结构进行比较，在保证两者度分布序列相同的情况下来度量实证网络社团划分质量与社团结构强度。从这个角度看，对社团结构影响起决定性作用的微观性质是匹配系数、聚类系数和更高阶微观特性，因此本文并没有将度序列对社团结构贡献进行量化。

图2 为基于零模型和中介效应分析的微观结构对社团特性影响的量化解耦分析框架。

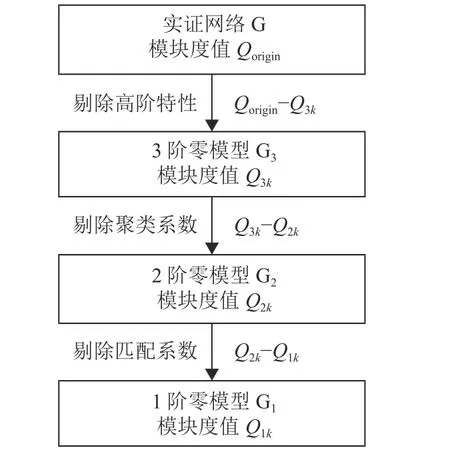
图2 基于零模型和中介效应分析的微观结构对社团特性影响量化解耦分析研究框架

如图2 所示，首先，通过构建实证网络的3 阶零模型剔除掉高阶微观特性，用实证网络与其3 阶零模型的模块度值Q的差值 ΔQ/(Qorigin-Q3k)量化高阶微观特性对实证网络社团结构产生的贡献。其次，通过构建此3 阶零模型的2 阶零模型剔除掉聚类特性，用3 阶零模型与其2 阶零模型的模块度值Q的差值 ΔQ=Q3k-Q2k量化聚类特性对实证网络社团结构产生的贡献。之后，通过构建此2 阶零模型的1 阶零模型剔除掉匹配特性，用2 阶零模型与其1 阶零模型的模块度值Q的 差值 ΔQ=Q2k-Q1k量化匹配特性对实证网络社团结构产生的贡献。最后，利用剔除各微观特性的网络间模块度值差值ΔQ与实证网络和其1 阶零模型的模块度值差值做比值即 ΔQ/(Qorigin-Q1k)量化出各微观特性（高阶特性、聚类系数、匹配系数）对各社团结构显著性类型实证社团结构产生的贡献比例。

下面利用以上的微观结构对社团特性影响的量化分析框架，实现各社团结构显著性网络的微观结构特性（高阶特性、聚类系数、匹配系数）对其社团特性产生的具体贡献程度的量化以及相对贡献程度的量化。对于不具有社团结构显著性网络，度序列对其社团结构起决定性作用，考虑到度分布是Q值计算的基础，匹配系数、聚类系数和更高阶特性对社团结构贡献特别小几乎为零，本文没有对它们的贡献进行量化。

对于具有1 阶社团结构显著性网络，匹配系数对其社团结构起决定性作用，聚类系数和更高阶特性对社团结构贡献特别小几乎为零，本文没有对它们的贡献进行量化，只需用其2 阶零模型与其1 阶零模型的模块度值Q的 差值 ΔQ=Q2k-Q1k量化匹配特性对实证网络社团结构产生的贡献。

对于具有2 阶社团结构显著性网络，聚类系数对其社团结构产生起决定性作用，更高阶特性对社团结构产生贡献特别小几乎为零，本文没有对它的贡献进行量化，使用微观结构对社团特性量化分析框架，计算出 ΔQ=Q2k-Q1k与 ΔQ=Q3k-Q2k量化出匹配系数、聚类系数对其社团结构产生的具体贡献数值，再使用 ΔQ/(Qorigin-Q1k)量化出匹配系数、聚类系数对社团结构特性的相对贡献程度。

对于具有3 阶社团结构显著性网络，更高阶特性分别对其社团结构产生起决定性作用，同理，使用微观结构对社团特性影响量化分析框架，量化出各微观特性（高阶特性、聚类系数、匹配系数）对具有3 阶社团结构显著性的实证网络社团结构产生的贡献具体数值 ΔQ， 再使用 ΔQ与原始实证网络和其1 阶零模型的模块度差值做除法得到ΔQ/(Qorigin-Q1k)量化出各微观结构对社团特性相对贡献程度。

3.3 实证结果分析

考虑到2 阶社团结构显著性网络中除社交网络外其他网络数量都极少，对少数网络进行分析可能不具有代表性，本文只对具有2 阶社团结构显著性的118 个社交网络完成匹配系数、聚类系数对社团结构贡献的平均比例分布进行分析。实验结果发现，对于这118 个具有2 阶社团结构显著性的社交网络而言，其微观特性中匹配系数比聚类系数对社团结构的贡献程度更大，约占总贡献的68%，而聚类系数对社团结构的贡献只占32%。

图3 依次为前面的具有3 阶社团结构显著性的10 个信息网络、93 个生物网络、27 个交通网络、57 个科技网络、106 个经济网络的微观特性（匹配系数、聚类系数、更高阶微观特性）对社团结构贡献的平均比例分布图。从图中可以看出，在具有3 阶社团结构显著性的5 种类型网络中信息网络的微观特性对社团结构贡献分布较特殊。在信息网络的微观特性中聚类系数对社团结构的贡献最大，其次是更高阶微观特性，最后是匹配系数。但在其他4 类网络中更高阶微观特性对社团结构的贡献相对最大，且这种现象在经济网络中表现尤为明显，其更高阶微观特性对社团结构的贡献占总贡献的90%左右。除了更高阶微观特性的贡献外，在这4 类网络中，生物、科技、交通网络的聚类系数对社团结构的贡献是最大的，匹配系数的贡献非常小。而经济网络正相反，除了更高阶微观特性外，匹配系数对社团结构的贡献最大，聚类系数的贡献非常小。

图3 具有3 阶社团结构显著性的各类网络微观特性对社团结构产生的贡献比例分布图

4 结 束 语

本文在实验数据选择方面使用社交、生物、科技、交通、经济、信息6 类不同规模的具有代表性的550 个实证网络进行实验，从定性和定量角度分析微观特性对社团结构的影响，大数据集也使结果具有鲁棒性、研究结论具有通用性。

本文首先基于零模型和显著性检验方法完成社团结构显著性检验，实现不同类型网络微观结构对社团特性影响的定性分析。该结果对此前研究中聚类系数即可刻画社团结构的结论有所修正，说明尽管聚类系数特性对于网络社团结构有很强的影响，但是并不足以充分揭示除社交网络之外的其他类型网络的社团特性的主要起源。

在具有不同社团结构显著性的各类型网络的基础上，本文提出了基于零模型和中介效应分析的微观结构对社团特性影响的量化分析方法，量化出各社团结构显著性类型网络的各微观结构对社团特性产生的贡献具体数值以及相对贡献程度。这种方法实现了对各阶微观结构对社团特性产生贡献程度的量化。