基于最小沟道的电网通信业务路由优化及应用

秦亚梅，汪 辉，李振伟，张 闻

(1.电子科技大学数学科学学院 成都 611731；2.国网安徽省电力有限公司信息通信分公司 合肥 230022)

电力通信网络主要由SDH（synchronous digital hierarchy）光传输系统和OTN（optical transport network）光传输系统组成，其与电力系统的生产、调度、运行、管理、沟通、协调等有着密切的联系[1]。因此电力通信系统对其使用的业务路由规划有严格的风险管控要求[2]。目前安徽电网业务路由的调整及新增，基本上都是基于业务路由最短路径原则[3]进行决策，缺乏有效的评估工具和仿真测试条件。上述处理原则给城域光网络业务的稳定性带来较大隐患（业务主用路由和备用路由共沟道）。同时，国家相关法律明文规定：公共区域不得随意破土施工，也导致城区光缆在敷设时存在共沟道（井）现象，因此亟需研究适合城域光网络SDH 传输系统的业务路由优化算法及仿真测试工具，为电力网络建设与业务运行方式优化提供理论参考和数据支撑。

目前电力通信业务通信方式主要是采用点对点的通信模式，为了使业务可靠稳定地传输，通常需要对业务路由（通道）使用相应的保护策略。保护策略主要分为通道保护和复用段保护。业务通道保护配置一般要求其主备路由满足共享风险链路组（shared risk link groups, SRLG）分离原则[4-6]。SRLG物理含义为共享相同传输设备、光缆、管道（沟道井）等物理资源的一组链路。本文主要研究城域光网络中业务的主备路由在无法严格满足SRLR 分离原则时，如何最小化其共沟道数量问题。

近年来，电力通信网络的业务路由规划及优化问题引起了国内外学者广泛地关注。文献[7]提出基于强化学习的多条件约束的业务路由优化算法。虽然考虑了链路风险权值、节点风险权值、网络带宽状态，但该模型不能解决物理光路共沟道情况下的业务路由规划问题。文献[8]设计出了光网络规划及仿真软件，但该软件偏向光传输的物理特性仿真分析以及网络建设成本控制。文献[9]提出了一种基于混合整数线性规划的多播路由与保护联合优化算法，在满足共享风险链路组条件约束下，提高了业务通信信道资源利用率，但并不适用于解决本文提出的工程问题。文献[10]提出了一种高斯-塞德尔迭代（Gauss-Seidel method）算法来解决路由规划问题，但该算法主要适用于基于TCP/IP 传输协议的路由规划，无法应用于电接口的业务路由规划。文献[11]对电力通信SDH 传输系统的自愈技术进行了深入研究，设计出一款基于B/S 架构的SDH 传输系统的自愈模型仿真系统，但它主要关注于SDH 传输系统功能的软件实现。文献[12]提出了多重不相交路径算法（multiple disjoint path algorithm, MDPAlg），该算法相比于迪杰斯特拉算法（Dijkstra）具有更高的运算速度，适合于大型网络拓扑应用，但是并没有对电力实际的业务场景进行验证，只是从理论上证明了其计算复杂度与可行性，并不适用于电接口的业务路由规划。文献[13]提出SDH 网络拓扑单元概念，并从网络风险值和网络均衡值等方面来衡量SDH网络风险与可靠性，但未给出具体的业务路由优化实施算法。文献[14]提出了基于K 条最短路径（K-shortest pathes,KSP）的风险均衡的业务路由分配算法，在实施的过程中会使用Dijkstra 算法选择K条备选路由，但算法选择的主备路由可能存在共节点或共链路风险。文献[15]提出了基于共享链路组与风险均衡的路由优化算法，其算法效果易受业务重要度指标的影响，对于城域光网络该指标项不易获取。

综上所述，开展适合城域光网络的电网业务路由优化技术研究是非常必要的。目前安徽电力通信网络的日常运维和业务配置较为简单，主要基于最短路径的原则进行业务路由安排，而此原则会导致业务的主备路由经过许多相同的光缆沟道井。同时城市的基础建设也很容易破坏电缆沟道井，如修建地铁、修建高架桥、修建道路、修建下水道、修建燃气沟道、自来水沟道改造、市政绿化施工等，给城域电力通信光缆及其承载的业务带来了诸多隐患。因此本文提出了基于最小光缆沟道的电网通信业务路由优化算法，算法使用融合排序的DFS 方法，在业务路由无法严格满足SRLG 分离原则时，最小化业务主备路由共沟道的数量。基于SRLG 的深度优先搜索算法（DFS-SRLG）能避免主备路由共链路和共节点风险，降低业务中断次数，对城域光拓扑调整及业务故障定位也具有重要的参考价值。同时，业务路由优化方法有利于提高业务管理人员的办事效率，提升调控运维人员事故处理能力，降低人工安排业务出错概率。最后，本算法在安徽电网的行政电话业务进行了应用，相对于默认的KSP 算法，显著降低了电话业务中断次数，提高了业务稳定性，对电网系统的稳定、安全、可靠运行具有重要的理论指导意义和实际应用价值。

1 业务路由优化算法

1.1 优化算法建模

1738 年，数学家欧拉解决了柯尼斯堡问题并创立图论。随着计算机的快速发展，图论已成为一门应用十分广泛的重要学科。人们也逐渐开始使用图论理论解决生活中遇到的实际生产问题。本文使用图论模型来解决基于最小沟道的电力通信业务主备路由优化问题。由于市政限制，城市内不能随意开挖沟道敷设光缆，导致部分光缆同沟道敷设。伴随着国家经济的快速发展，城市基础建设也在加快步伐。城市建设的过程中难免会破坏部分光缆，导致部分电力业务中断，因此如何尽可能降低业务中断次数、合理调整光网络拓扑、科学规划业务主备路由等问题急需解决。以安徽省内某市城域光网络传输拓扑为例进行说明，如图1 所示。为了保留拓扑连接关系和计算方便，图中简化了实际光缆铺设走向以及沟道位置坐标情况。图中，任意两个顶点之间代表一条完整的光路信息，忽略了两段光缆纤芯中间跳接情况，通信站代表光传输设备及光路传输方向。

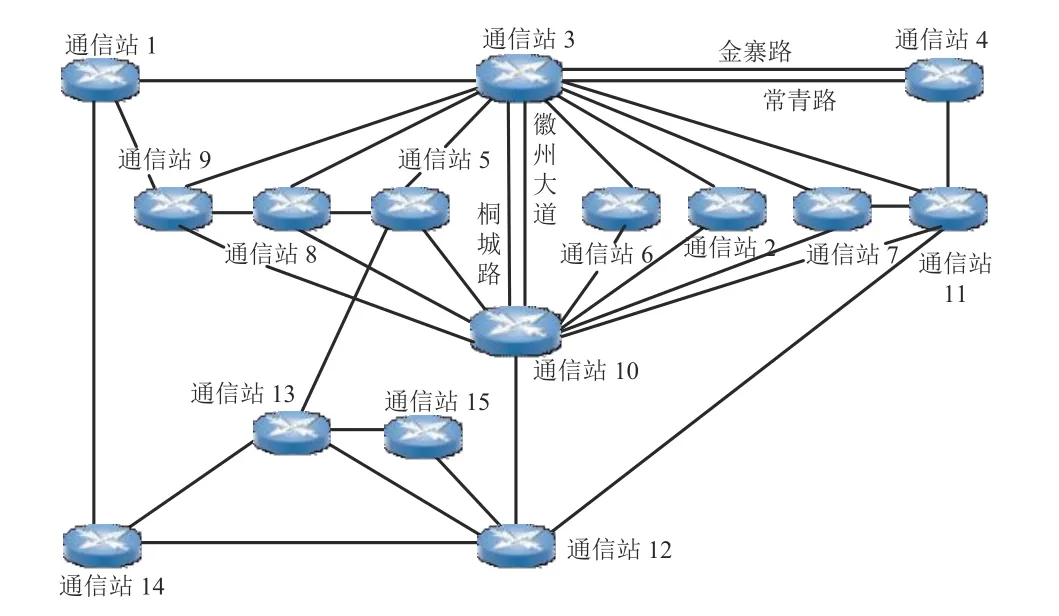
图1 城域光路拓扑图

本文使用无向图对城域光路拓扑图进行建模。为了解决多重边问题即区分通信站3 至通信站10 两条光路信息、通信站3 至通信站4 两条光路信息，任选其中一个光路中插入新的顶点信息，即引入虚拟节点方法解决无向图的多重边问题，最终简化后的拓扑模型如图2 所示。

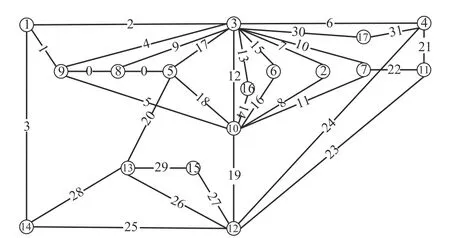
图2 光路拓扑图无向图模型

假设光网络拓扑图使用一个赋权无向图连通图G=(V,E,W)描 述，其中，V表示G中所有的顶点集合：V(G)={v1,v2,···v17}。 |V|=17, |E|=32分别表示图G的顶点和边数。无向图G=(V,E,W)边的集合可以 描 述 成E(G)={v1v3,v1v9,v1v14···,v13v15},vivj=vjvi,i,j∈V,W是G所有边对应权值的集合，其权值大小表示对应光路编号W={ω1,3,ω1,4,ω1,9,···,ω13,14,ω13,15}， 如 ω1,3=2表示节点1 至节点3 对应的光路编号是2，权值为0 表示该段光路使用尾纤直接连接，因为两个通信机房距离彼此靠近。每条光路对应的沟道井号是ca, ∀a∈E，具体数据格式请参照1.2 节。

在图论中，顶点vi的 度是与vi直接关联的边的数目，记为：TD(vi)。 从顶点vi到顶点vj的路径是一个顶点序列，路径（路由）的长度等于从一个顶点vi到另一个顶点vj所经过边的数量。第一个顶点到最后一个顶点相同的路径称为回路或环。序列中顶点不重复出现的路径称为简单路径。除了第一个顶点和最后一个顶点之外，其余顶点不重复出现的回路，称为简单回路或简单环。本文研究的问题是：当新开通的业务主备路由无法严格满足SRLR分离原则时，如何使业务主备路由经过相同编号的沟道井数量最少，其数学表达模型[16]为：

式中， ||表示求集合中元素数量。业务主备路由标签集K={1,2}，表示由主用路由和备用路由组成的集合。当k=1时 ，默认是主用路由编号；k=2时，则是备用路由编号。 δ+(i)代表是所有从点出发的边（弧）。由于顶点 { 16,17}是插入的虚拟顶点，所以图中物理真实节点N={1,2,3,···,15}，N表示图1 中通信机房组成的集合。 δ-(i)代 表所有进入顶点vi的边。是 决策变量：路由k经过边a，则为1，否则为0。o表示新开通业务的起始站点，d表示业务终止站点d∈N,o≠d≠i。δ+(S):{(i,j)|(i,j)∈E,i∈S,j∈S,i≠j}（是点集合）。式(2)表示主备路由不能同时经过相同的边，即每个边只能遍历一次；式(3)表示如果顶点vi既不是起始点又不是终止点，那么进入该顶点流与出去流相等； 式(4)和式(5)表示主备路由必须从顶点o出 发，回到顶点d，不能停留在某个顶点（节点）；式(6)表示消除子回路，避免主用路由或者备用路由形成环路。式(7)表示整数约束。式(8)表示G中任意顶点至少有两个直接关联的边。

定理 1 若一个无向连通图G=(V,E)存在一个最大简单环，且除最大简单环上的其他顶点均与最大环相交，则在图G=(V,E)中任意两个顶点至少存在两条路径。

证明：除去最大简单环包括的顶点，其余顶点的边与最大环上的顶点可以组成新的环并与最大简单环相交或者相切，由于环上任意两点一定存在顺时针和逆时针的两条路径，所以图G=(V,E)中任意两个顶点至少存在两条路径。

为了方便讨论式(1)解的存在性，现对图2 进行简单处理，结果如图3 所示，其中粗线是最大简单环。下面对式(1)解的存在性进行讨论。

图3 包含最大环的光路拓扑图

1）唯一解：如果无向连通图G=(V,E)存在哈密顿圈[17]，且图的顶点数量等于边的数量 |V|=|E|，则式(1)只存在唯一解。

2）无解：如果无向连通图G=(V,E)存 在|V|>|E|，则式(1)无解。

3）非唯一解：如果无向连通图G=(V,E)存在最大简单环，且经过除最大环上的顶点的环与最大环相交或者相切，则式(1)的解可能不唯一。当式(1)存在非唯一解时，由于主用路由和备用路由都是按照路径长度进行升序排列的（默认情况下图G=(V,E)中所有边对应的长度是1），所以式(1)的解是基于主用路由和备用路由的路径长度之和最小原则，选择出合适的解。

1.2 数据预处理

由于网络拓扑中光路以及光路对应光缆走向的电缆沟道井的数据都是使用文字进行描述，不利于算法数据处理，所以需要对光路和电缆沟道井建立一种专用的数据映射（全局编码，使用Excel 的IFERROR(VLOOKUP(A2,IF({1,0},A $1 :A1,E $1:E1),2,0), MAX(E $1:E1)+1)函数嵌套进行处理，其功能是第一次出现的名称按顺序编号，非第一次出现的名称使用第一次出现时所编的编号），即相同的数据（光路、沟道井）使用相同的编号。每段光路对应的沟道井编号最终映射成集合ca,∀a∈E。拓扑之间的关联信息使用邻接矩阵Mnb进行表示。数据的存储使用矩阵格式，光路与沟道位置具体的映射关系如图4 所示。

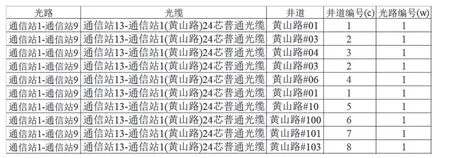
图4 数据预处理图

1.3 算法描述

本文提出的DFS-SRLG 算法主要思想是：业务的主用路由和备用路由，在无法严格满足SRLG分离原则时，最小化主备路由共沟道的数量。即使用DFS-SRLG 算法选出业务从起始点（通信站）到终止点（通信站）的所有路径（路由），然后基于共沟道井数量最小化原则，选择2 条路由分别作为业务的主用路由和备用路由。此算法不仅适用于电力通信城域网的业务路由规划，也适用于光路网络布局合理性的验证，并以此作为优化的理论依据。DFS-SRLG 算法具体流程图如图5 所示。

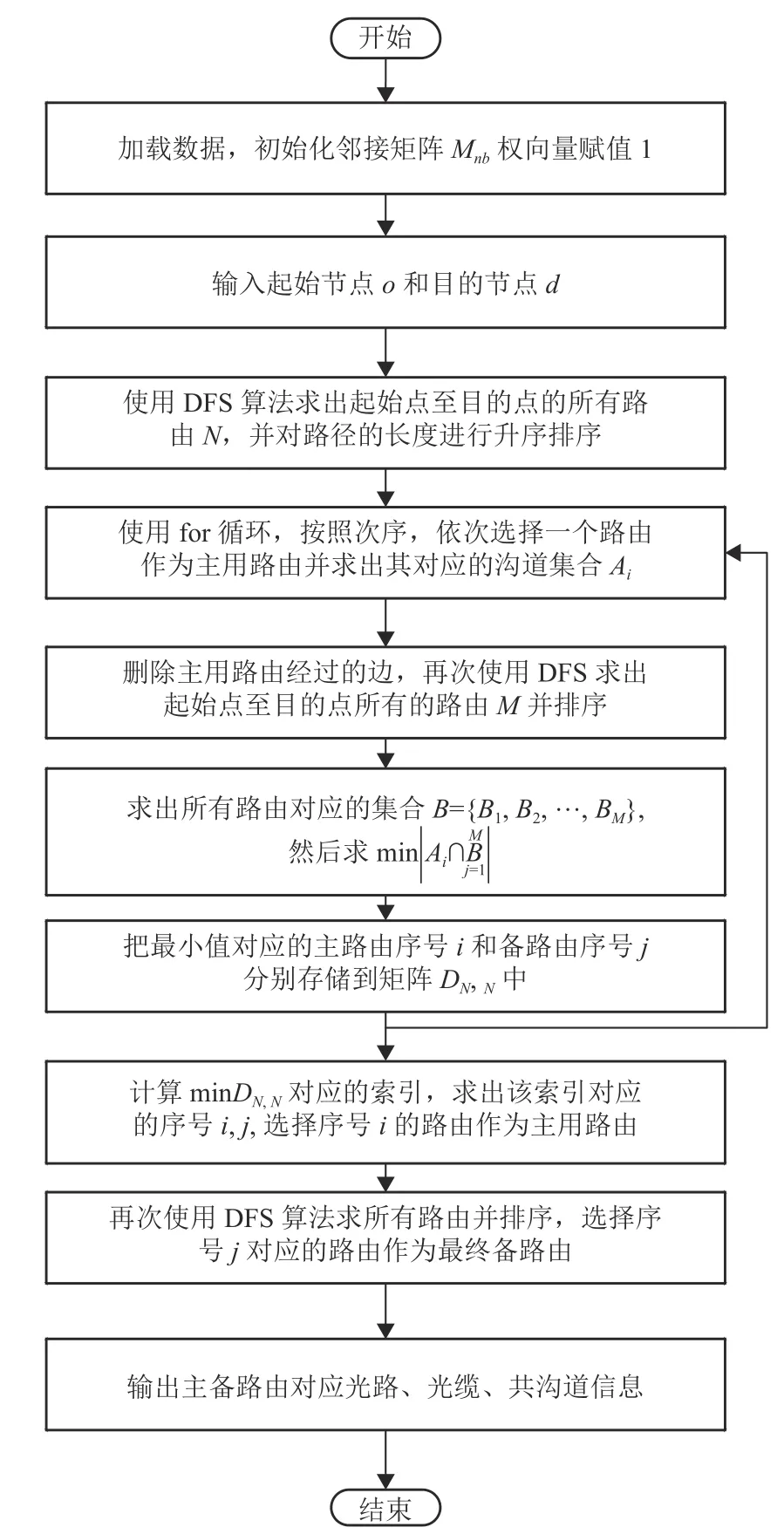
图5 DFS-SRLG 算法流程图

DFS-SRLG 算法能在从起始点到终止点的所有路径中，选择出光路共沟道数量最少的2 条路由，并把第一条路径作为主用路由，第二条路径作为备用路由，同时展示出主备路由承载的光缆信息和经过的沟道井信息。此算法不仅极大地降低了整体业务中断风险，还避免了工作路由优先[18]（active path first, APF）算法的缺陷，提升了网络稳定性。

2 算法分析

2.1 算法仿真参数分析

本文基于安徽某个城市的城域电力网络进行仿真实验，具体光路拓扑图如图1 所示，其对应的图模型如图2 所示。该网络包含15 个实际存在的中心站节点和30 条真实存在的光缆链路，并且每个节点的度大于等于2，所以从起始点至终止点肯定存在两条路由。仿真分两种情况进行讨论：一是主备路径最短优化（KSP 算法，网管运维人员默认使用的算法）；二是尽量满足SRLG 分离原则，使主备路由所共沟道井数量最小化算法（DFS-SRLG）。选择起始点通信站1 至终止点通信站3 的行政电话业务进行理论仿真分析，其主备路由信息的仿真结果如图6 和图7 所示。

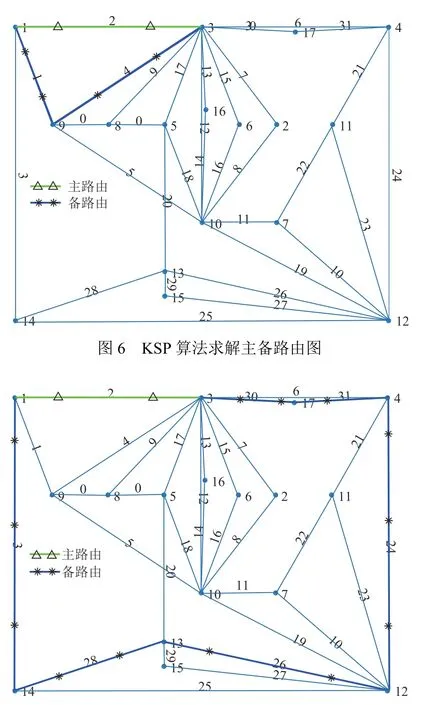
图7 DFS-SRLG 算法求解主备路由图

使用KSP 算法主备路由共井数量为11 个，而使用DFS-SRLG 算法主备路由共井数量为1 个，业务主备路由对应的光缆信息如图8 所示。从仿真结果可以看出使用DFS-SRLG 算法可以显著降低主备路由共沟道数量，降低业务中断风险。同时该结果也对光路拓扑进行合理规划具有一定的指导意义，可根据业务主备路由共沟道井情况，结合检修计划调整共沟道井光路。

图8 主备路由对应的光缆信息

由图3 可知：基于行政电话业务优化可能存在多解。当存在非唯一解时，本文基于主备路由所对应的路径长度之和最小原则，选择出一组解作为行政电话业务的主备路由。同时，基于所有业务重要度相同的原则下进行研讨，虽然未考虑业务重要度的差异性，但本文在求解最小值时，保留了所有主备路由共沟道数量DN,N，也可通过求解次小值来简单处理不同重要度业务的路由安排，下一步将对于业务重要度有差异进行深入研究。

2.2 算法应用分析

本文算法是为了解决实际问题而提出的，下面需要对算法实际应用效果进行分析。由于2019 年新型冠状病毒暴发后，行政电话及视频会议对办公人员起到了很大的作用，于是把算法首先应用到行政电话业务上，表1 是现场运维人员对2020 年至2022 年行政电话业务中断次数进行统计的结果。2022 年1 月使用DFS-SRLG 算法对行政电话业务进行了优化改造，截至2022 年7 月行政电话业务中断只发生了4 次。

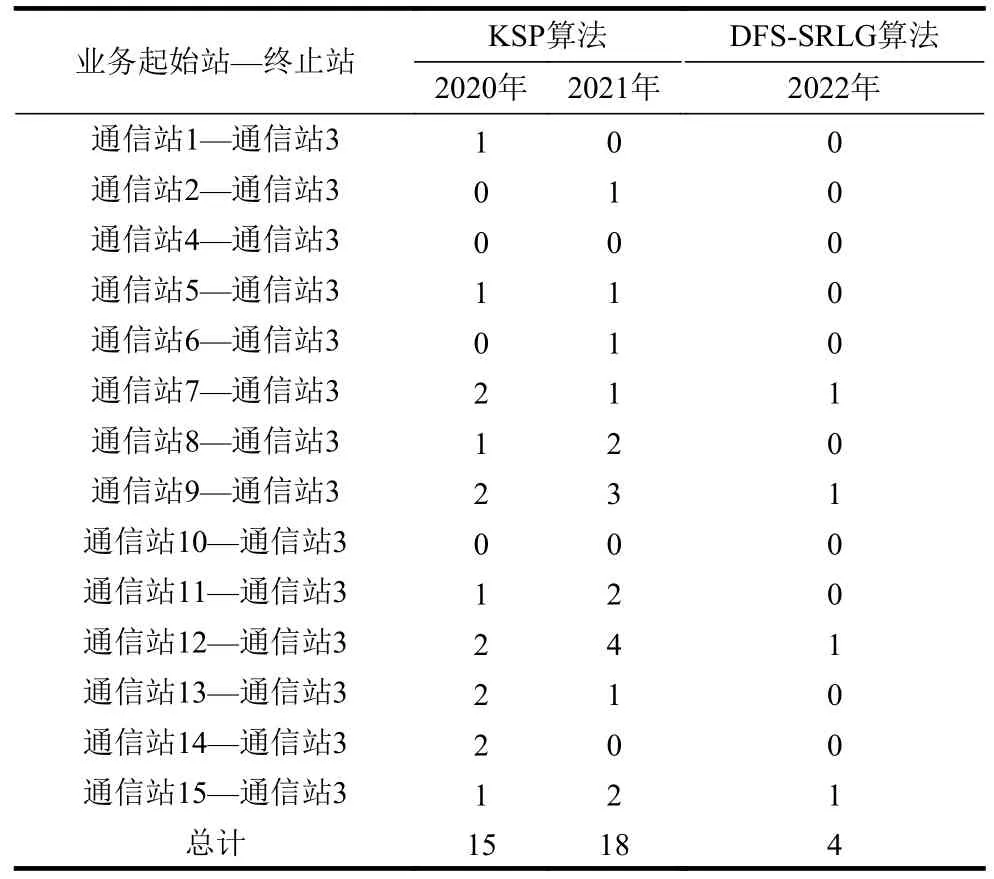
表1 行政电话业务中断次数统计表

从表1 统计的结果可以看出：行政电话业务在使用DFS-SRLG 算法后能显著降低其中断次数，说明DFS-SRLG 能有效地降低整体业务中断风险，解决了实际生产问题。

2.3 算法复杂度分析

3 结 束 语

本文提出的业务路由规划算法可以实现业务路由的动态规划，在一定程度上简化网络业务管理，降低运营成本，提高整体业务的安全性。DFSSRLG 算法不仅可以降低平均整体业务中断风险，提高网络的稳定性，还为光缆拓扑调整和业务故障定位提供了理论指导。