基于力矩密度曲线的轻型机械臂的统一优化方法
周翔群,尹海斌,2
(1.武汉理工大学 机电工程学院,湖北 武汉 430070;2.湖北省数字制造重点实验室,湖北 武汉 430070)
随着机械臂技术的不断成熟,其使用场景越来越丰富,如何提高机械臂的动态性能和降低能耗成为研究的主要问题,而机械臂的轻量化设计对于经济性和动态性能是非常重要的。机械臂轻量化的主要研究方向包含:用轻型材料、少用材料[1]、驱动系统的选择或优化来匹配最优结构[2]。轻型材料和少用材料都是通过结构优化实现轻量化的目的,通过驱动系统优化主要是通过提升机械臂驱动系统的力矩密度来达到目的。
在结构优化中,铝合金和碳纤维等具有低密度、高强度的轻型材料被用于设计机械臂[2],但其造价高和工艺不成熟的特点限制了其应用。而通过少用材料的方法容易导致机械臂产生不确定性振动。通过结构优化、轨迹规划等方法可减少不确定性振动,但并不能够完全消除柔性振动。
除结构外,驱动系统也是重点研究对象,如电机结构优化、拓扑结构和控制[3]被用来增加电机的力矩密度,但未考虑与减速机的集成。Roos等[4]提出了一种匹配给定负载的最优减速机传动比的方法。Zhou等[5]提出了一种集成方法来设计轻型类人机械臂,该方法同时优化了结构和驱动系统。Yin等[6-7]用连续的驱动系统变量来快速计算轻型机械臂的全局最优解。
笔者在先前的研究基础上考虑连续驱动系统变量的同时,考虑了结构变量和运动学分析。通过对连续的驱动系统变量分别采用两种力矩密度曲线来描述并进行比较,并且还考虑了连杆和关节壳的结构变量。基于运动学分析,将结构优化用于动态计算中来确定驱动系统设计变量的值,驱动系统设计变量的值与结构参数相互影响。因此,利用力矩密度曲线可以确定驱动系统的质量和惯量,同时驱动系统的质量和惯量用于动态计算中并反复被更新直到问题收敛。最后通过实验和案例来验证这种优化方法。
1 结构和驱动系统的统一描述
机械臂的轻量化设计主要有3种方法,分别是只考虑结构优化、只考虑驱动系统优化和综合考虑结构和驱动系统的优化。为了减少优化中的无序计算,需要一种结构和驱动系统的统一描述,如图1所示。在图1中,机械臂结构动力学被描述为:
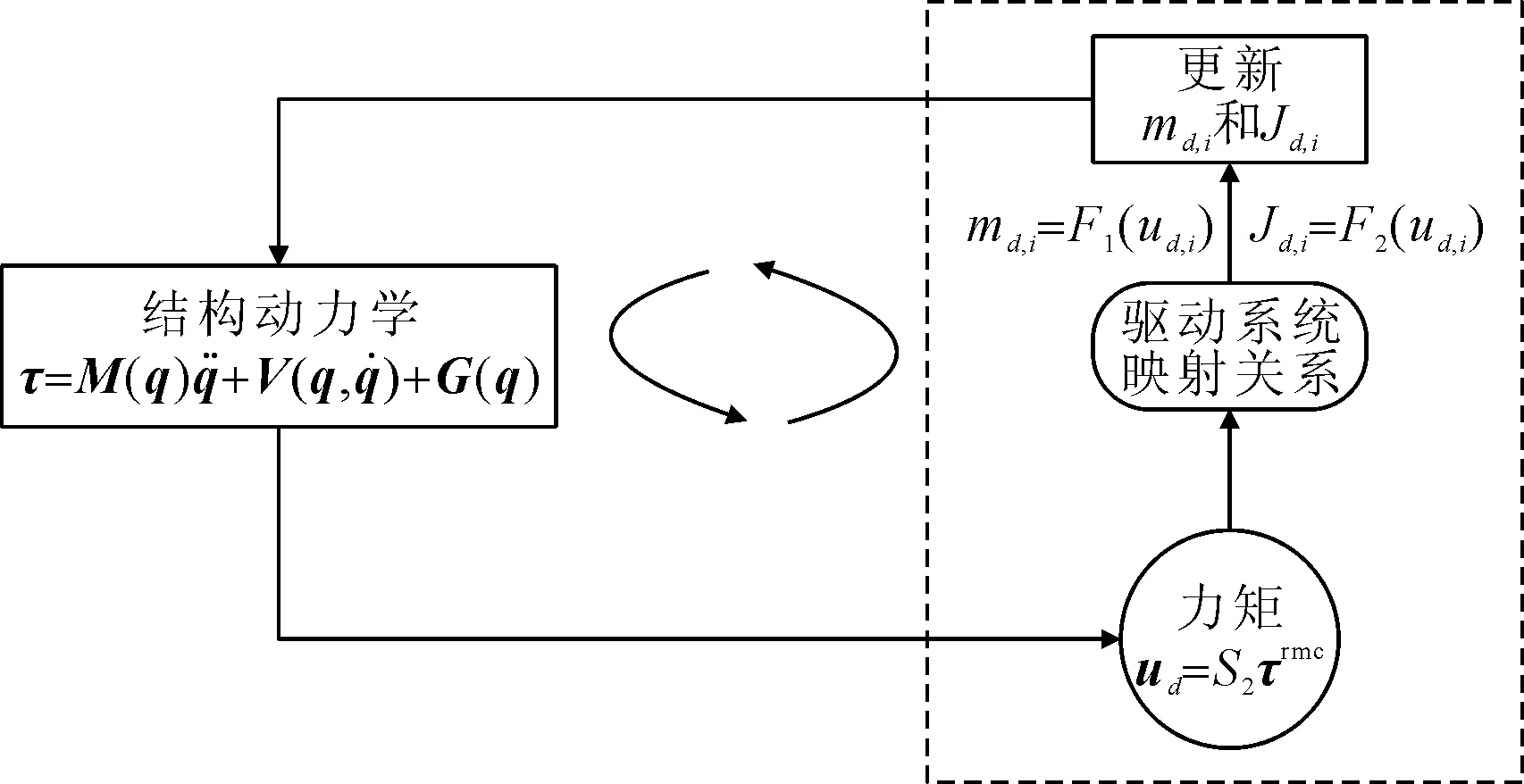
图1 结构和驱动系统的统一描述
(1)
式中:M、V和G分别为惯量、非线性和重力相关项矢量。q和τ分别为n个自由度坐标和n个驱动系统的力矩,即q∈Rn和τ∈Rn。
结构动力学用来计算得到驱动系统的额定力矩,表示如下:
ud=S2τrmc
(2)
式中:τrmc为结构动力学计算中所需力矩的均方根;ud为电机工作在额定状态时驱动系统的额定力矩;S2为安全系数。
额定力矩用于更新第i个驱动系统的质量md,i和惯量Jd,i,在结构动力学计算中其初始值被假定为预估值。为了实现更新,需要获得额定力矩ud,i与驱动系统的质量和惯量之间的映射关系。根据电机的力矩密度和减速机配对原则[5],映射关系描述为:
mm,i={md-mg}i
(3)
式中:Cm和Cj分别为电机冷却条件和拓扑结构的常数;ρm和rm分别为电机的平均密度和定子半径;ζ和η分别为驱动系统的减速比和平均效率;mg和Jg分别为减速机的质量和惯量,mm和Jm分别为电机的质量和惯量。
这些映射关系与驱动系统使用的材料、拓扑结构和技术参数有关。对于特定驱动系统类型,映射关系可以被定义和描述为md,i=F1(ud,i) 和Jd,i=F2(ud,i),其中,F1和F2为映射函数。
映射关系是驱动系统的额定力矩与结构动力学中的质量或惯量之间的联系纽带,并能够使机械臂在质量上统一评估。因此,这个映射函数被用来建立机械臂的统一描述。
2 统一优化方法
基于统一描述,提出一种统一优化的方法。为了阐述这种统一优化方法,机械臂的拓扑结构假设为串联,如图2所示。
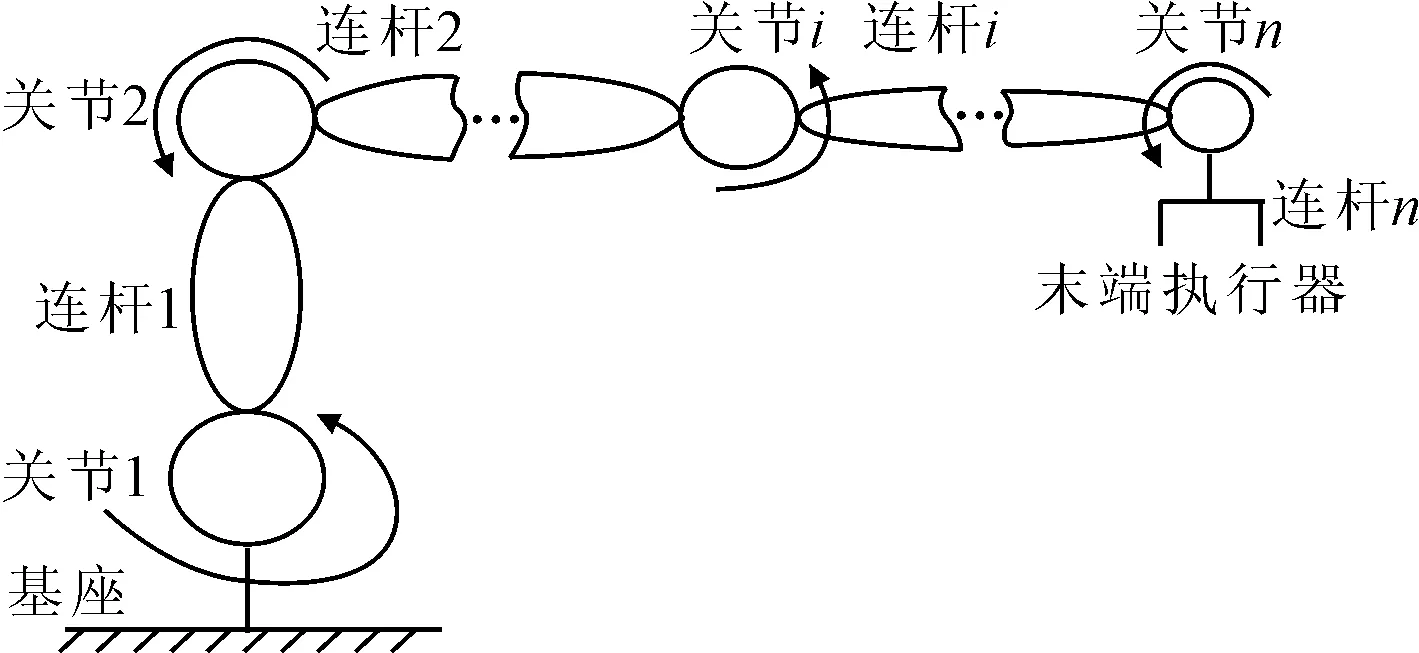
图2 具有n个连杆和n个驱动系统的串联机械臂
2.1 设计变量
(1)结构设计变量us。机械臂结构变量定义如图3所示。

图3 第i个连杆的结构尺寸
图3表示长度为li的第i个连杆的结构尺寸。机械臂中的管和槽的参数定义为设计变量uo=[r1,a1,b1,…,ri,ai,bi,…]。除了管和槽的设计变量uo,结构设计变量us还包括关节壳变量uh,这些变量不是独立变量,而是依赖于驱动系统的设计变量ud。进一步,连杆的长度变量ul=[l1,…,li,…]也包含在结构设计变量中。因此,结构设计变量被定义为us=[uo,uh,ul]。
(2)驱动系统的设计变量ud。本文驱动系统的设计采用模块化的方法来提高设计效率,图4展示了模块化关节的详细配置。驱动系统安装于关节壳中,因此,关节壳变量uh与驱动系统的设计变量ud有关。后者为驱动系统的额定力矩,它被描述为ud=[ud1,ud2,…,udi,…],前者为关节壳的相关结构尺寸并被定义为:
uh=[Rh1,Wh1,δh1,Δh1,…,Rhi,Whi,δhi,Δhi,…]
(4)
在额定力矩作用下,考虑到强度和刚度约束条件,厚度尺寸(δhi和Δhi)根据先前的研究确定[8]。考虑减速机的装配间隙以及轻量化的目标,关节壳的半径和宽度描述为:
(5)
式中:Rgk和Wgk分别为第k个候选驱动系统的减速机的最大半径和宽度;当第i个关节是T或者H类型时,δ对应地被给定为δT=1(δH=0)或者δH=1(δT=0)。
驱动系统的减速机尺寸与其额定力矩相关,但在优化中不需要连续映射减速机的尺寸。只利用其额定力矩的范围来决定减速机的尺寸(Rgk和Wgk),描述为:
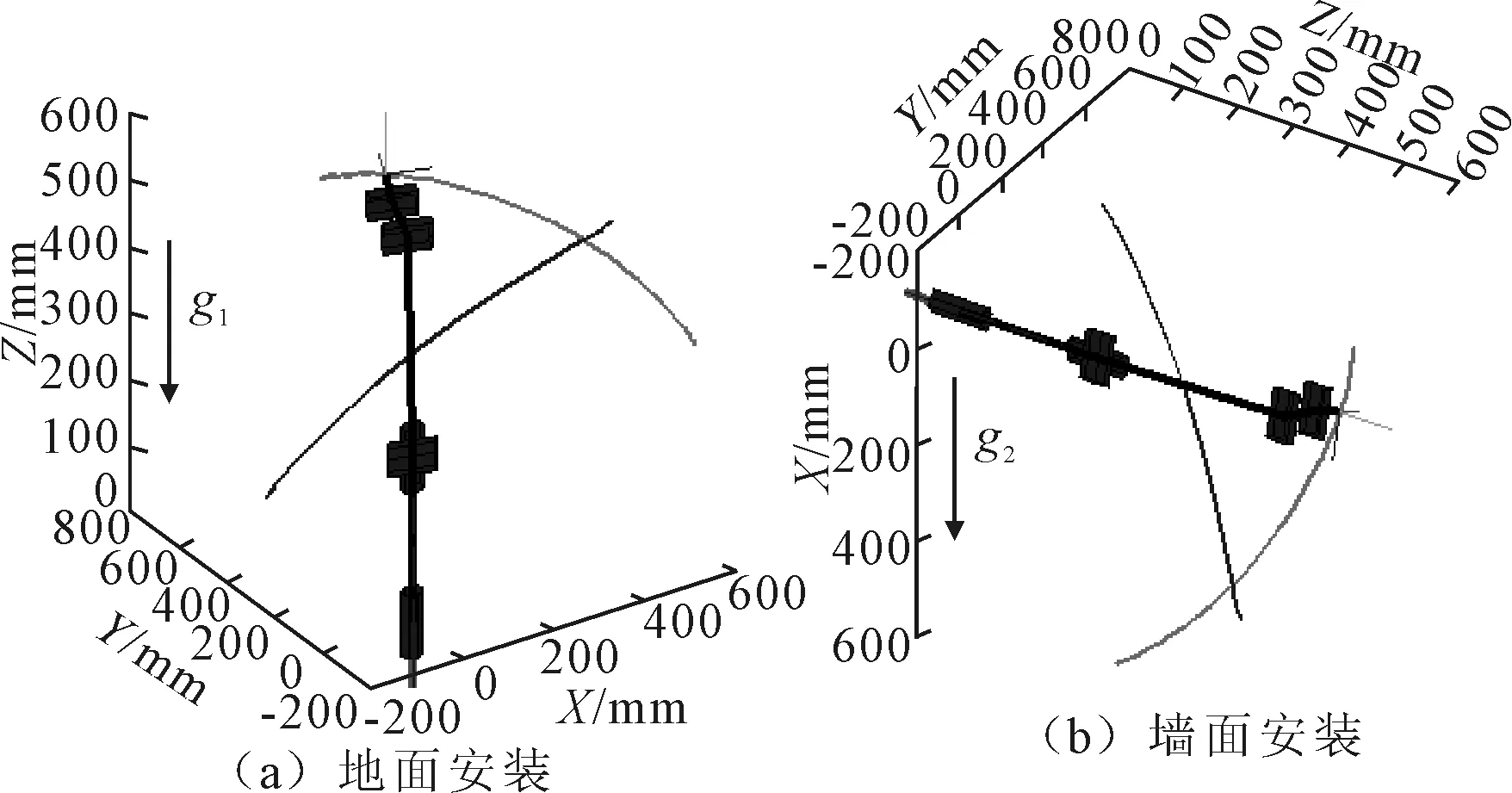
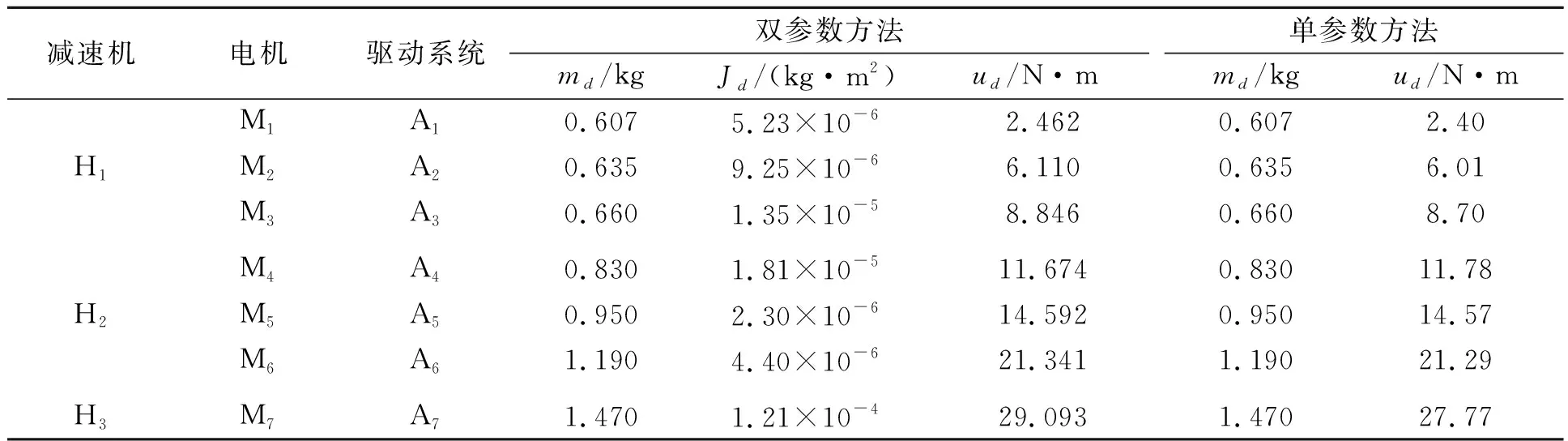
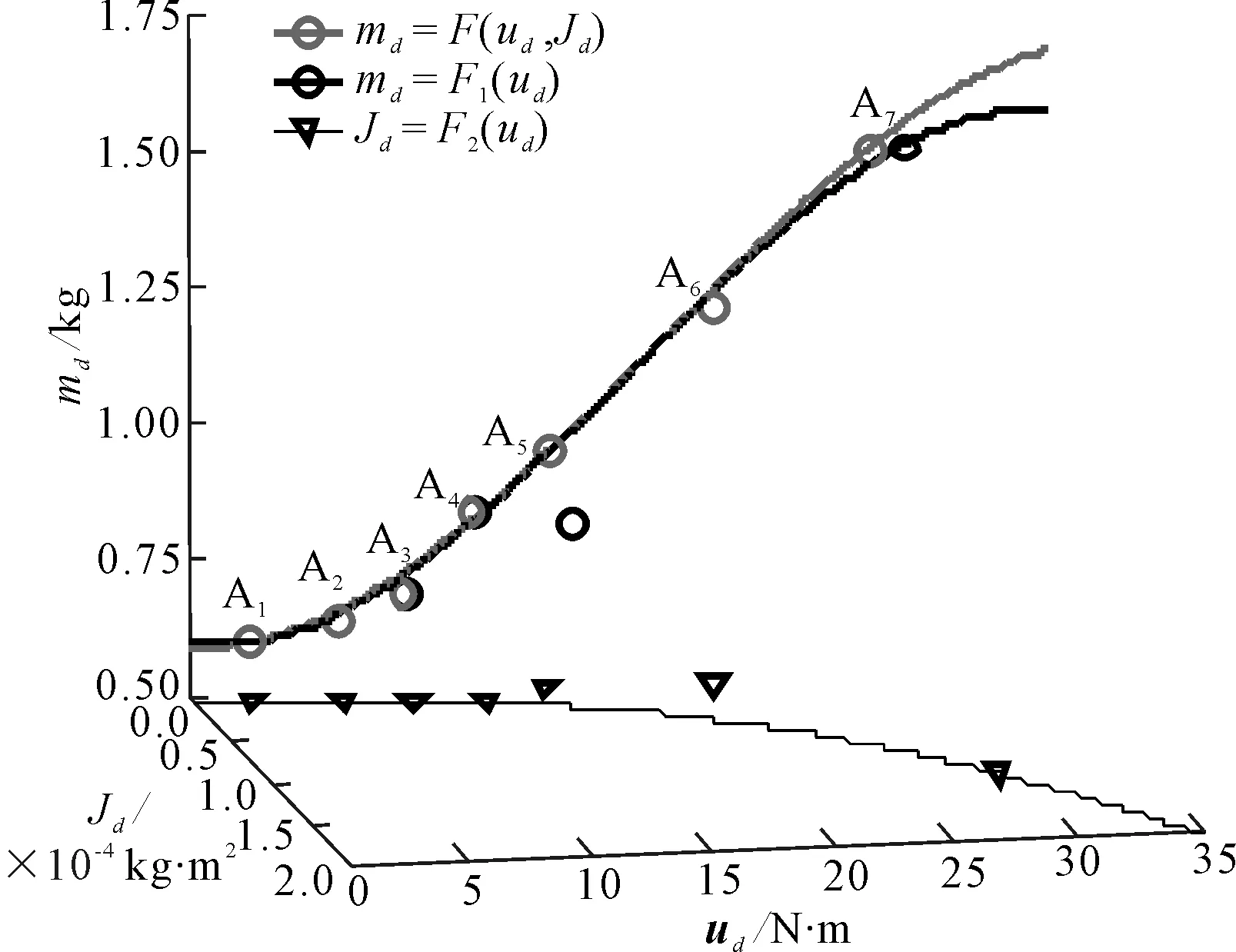
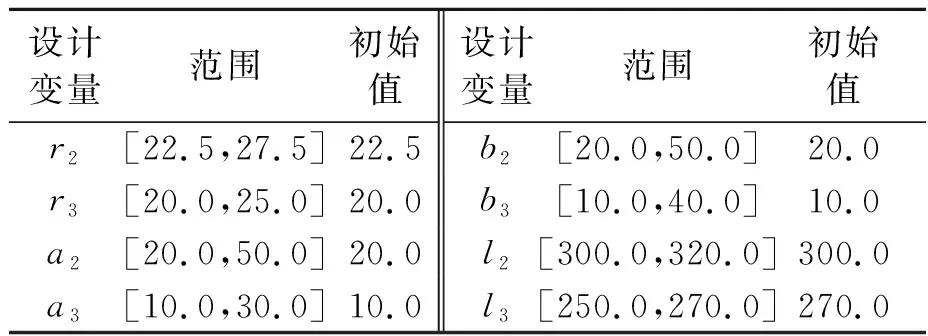
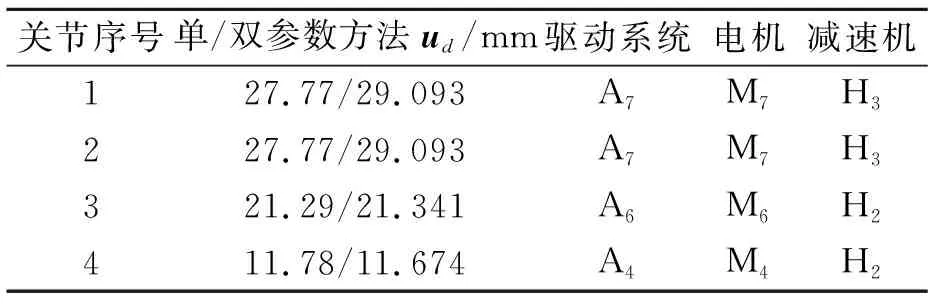
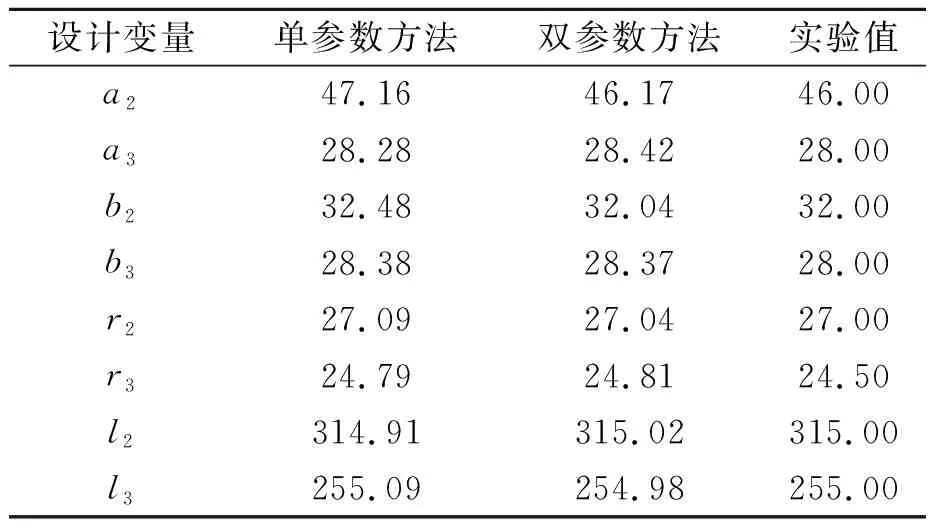
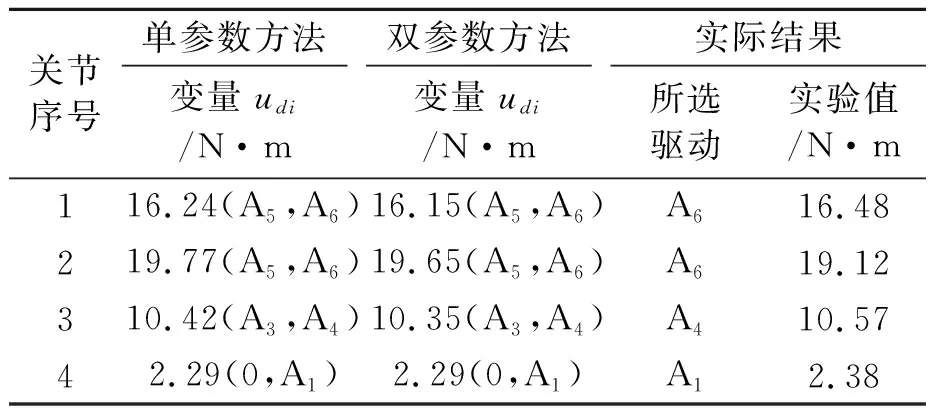
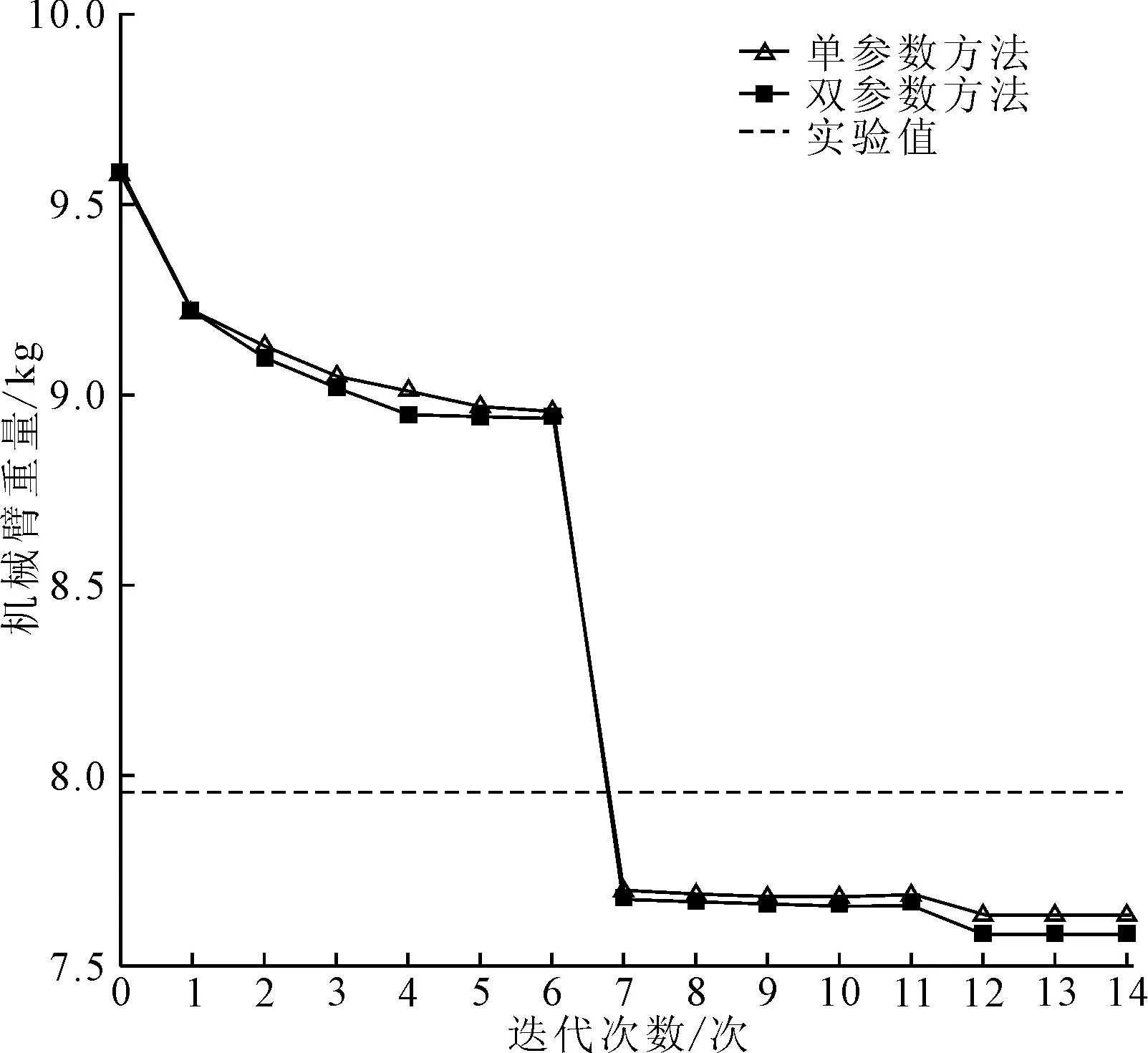
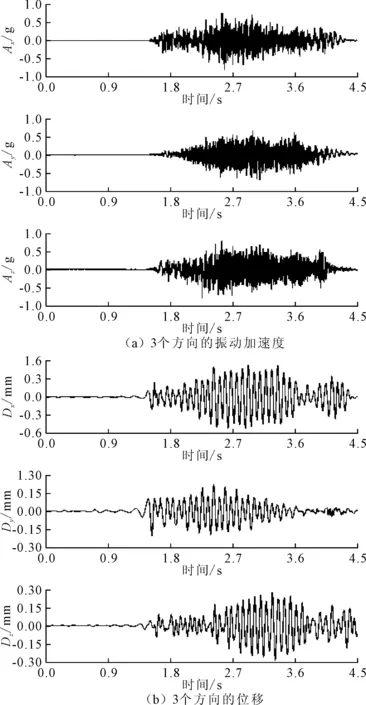
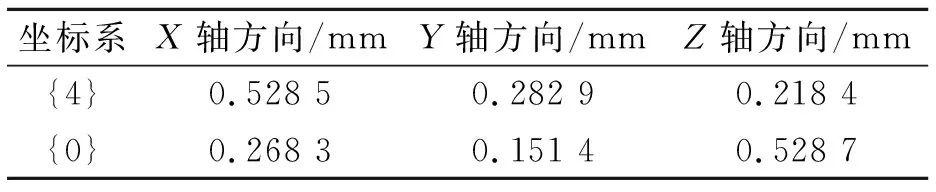
Td(k-1) (6) 式中,Tdk为第k个候选驱动系统的额定力矩。 根据式(4)~式(6),uh和ud的关系被描述为: uh=Fc(ud) (7) 因此,机械臂的设计变量主要由矢量X=[us,ud]表示,其中,us=[uo,uh,ul]和ud分别为结构和驱动系统的设计变量。 为保证机械臂的工作空间、结构强度和刚度不发生变化。因此,在优化中需要设定一些约束条件来限制其变化。而分析这些变化需要提供一些输入条件,例如负载和轨迹。负载作为设计条件之一标记为b,而且,运动轨迹被定义为抓取和定位操作的关节路径,它从t=T1时刻的起始位置qs到t=T2时刻的终止位置qe。在轻量化设计中,这些关节轨迹被规划为平滑曲线来减小所需力矩。于是,这些光滑的轨迹被描述为: qj(t)=c0+c1t+c2t2+c3t3+c4t4+c5t5 (8) 式中:qj为第j个关节的轨迹;第j个关节轨迹系数被描述为向量Cj=[c0,c1,c2,c3,c4,c5];六维向量可以由6个参数来确定,即分别为起始和终止点的位置、速度和加速度。 考虑关节轨迹,机械臂的工作空间需要满足以下条件: ≥Cmin (9) 式中:m为离散点的数量;J(q,ul)为雅可比矩阵;Cmin为最小可接受的全局条件指标GCI[9];q为关节轨迹矢量。 此外,机械臂的结构强度和刚度约束条件可描述为: S1σm(X)≤σy,S1dm(X)≤dmp (10) 式中:σm为机械臂的最大等效应力;σy为材料的屈服强度;dm为机械臂最大变形;dmp为最大许可变形;S1为结构安全系数。 机械臂的目标函数描述如下: minh(X)=h1(us)+h2(ud) (11) 式中:h1(us)和h2(ud)分别为结构和驱动系统的质量;X为机械臂的所有设计变量。 设计变量需要满足式(9)和式(10)中所给出的约束条件和设计标准。而且,结构设计变量应该满足给定的范围要求。 (12) 其中,ulower和uupper分别为结构设计变量的下限和上限。为了在下面介绍设计方法中简化描述所有的约束条件、设计标准和给定范围,采用式(13)表述。 g(us,ud)≤0 (13) (1)单参数更新方法。当连杆的惯量占主导时,驱动系统的惯量也不是影响其自身所需要的力矩的主要参数。当串联机械臂的连杆具备细长特征时,根据力矩密度曲线md,i=F1(ud,i),只有驱动系统的质量被用来更新是合理的。考虑到驱动系统惯量的影响,驱动系统的力矩密度曲线被修正为md,i=F(ud,i,Jd,i),可表示为: (14) 式中:Jd,i为第i个驱动系统的惯量;参数αi为第i个关节轨迹的最大加速度。 由于在计算中只有质量被更新,因此将这种方法称作单参数更新方法。 (2)双参数更新方法。为了提高优化设计的精度,在结构动力学中驱动系统的质量和惯性都被考虑更新。因此,质量和惯量能够依据如式(3)所示的两条映射曲线来更新。将这种情况称为双参数更新方法。 图5描述了统一优化的流程,其中包括结构分析和动态计算。 图5 统一优化流程图 在结构分析中,当驱动系统的设计变量固定时,结构设计变量(us)被更新。在这个模块中,用ANSYS(non-linear programming by quadratic lagrangian)建立了一个参数化模型并且采用NLPQL算法加载约束条件,计算中,轨迹用于运动学分析来满足工作空间的需求,负载条件用来建立结构约束。最后,用遗传算法来搜寻有限元模型中的满足结构目标的最优解。 图6为四自由度串联机械臂的原理模型,其中,肩部有2个自由度,肘部有1个自由度,腕部有1个自由度和一个抓手。机械臂的最大可达距离为700 mm。在本设计中,关节1为T型驱动系统,另外3个关节为H型驱动系统。连杆2和3采用如图3所示的标准拓扑结构。同时,连杆1和4仅采用标准拓扑结构的上或下半部分,它们的长度给定为l1=250 mm,l4=130 mm。因此,关于连杆槽、长度和关节壳的设计变量分别表示为uo=[r2,a2,b2,r3,a3,b3],ul=[l2,l3],和uh=[Rh1,Wh1,δh1,Δh1,…,Rh4,Wh4,δh4,Δh4]。 图6 四自由度串联机械臂的原理模型 机械臂由材料屈服强度为σy=270 MPa的铝合金(6061-T6)制造来满足轻量化的需求,其最大的许可变形量设定为dmp=1 mm。目标负载设定为2 kg,其在末端抓手中作为一个质点。 机械臂的运动学和动力学仿真通过考虑一组轨迹来分析。如图7所示,机械臂有两类安装类型,其由重力矢量g1=[0,0,-1]和g2=[1,0,0]来区别,每个安装类型的机械臂沿着两种轨迹移动。因此,机械臂总共执行4种轨迹的运动。 图7 在地面和墙面安装下的两类轨迹 理论上,驱动系统的力矩密度曲线存在但它依赖于驱动系统的材料、拓扑结构和额定速度。而且,这些力矩密度曲线随着技术的发展而改进或变化。因此,基于一组反映当前技术的候选驱动系统的数据,本研究采用拟合曲线方法来给出驱动系统的力矩密度曲线。 图8 候选电机和谐波减速机的技术参数 驱动系统的质量md,惯量Jd,额定转矩ud分别由式(3)或式(14)计算,结果如表1所示。因此,7个待选驱动系统的参数由两种方法获得并用来拟合驱动系统的力矩密度曲线。 表1 候选驱动系统,电机和减速机的参数 选定驱动系统的力矩密度曲线矩如图9所示,双参数方法能够获得两条曲线md=F1(ud)和Jd=F2(ud),单参数方法由一条曲线md=F(ud,Jd)描述。md曲线均坐落于质量-力矩平面,Jd曲线坐落于惯量-力矩平面。两种方法的md曲线几乎重合,但用最大转动惯量计算标记为A7的候选驱动系统时两者之间最大的差值大约为4.5%。 图9 选定驱动系统的力矩密度曲线 为了评估结构强度和刚度约束,选择驱动系统、结构安全系数。安全系数被分别设定为S1=2和S2=1.3。此外,误差条件e被设定为0.000 1,Cmin被设定为0.28。 连杆设计变量的初始值和范围如表2所示。此外,在负载条件下给定结构参数初始值的机械臂伸展到极限位置时,采用静力学估算驱动系统的初始值如表3所示。在两种设计方法中,驱动系统初始设定为相同的部件,采用符号A代表,并且分别用相应的符号M和H标记电机和减速机组成。虽然驱动系统初始设定部件相同,但是两种方法的计算不同,优化中它们的表征参数即设计变量ud是不同的。 表2 连杆设计变量的初始值和范围 mm 表3 驱动系统设计变量的初始值 表4给出了关节壳设计变量的优化值,根据先前的研究[8]和式(5)确定的结果。 表4 关节壳的设计变量的最优值[8] 表5列出了连杆设计变量在两种方法中收敛的最优值与实验值。对于这两种方法,最优值几乎相同并且结果表明在一定精度条件下单参数方法能够替代双参数方法。实际中,由于两种方法都考虑了冗余度而且结果比较接近,因此,两种方法中的最优值都能够为实验中使用值提供参考。 表5 连杆设计变量的最优值 mm 机械臂有4个关节,每个关节的驱动系统设计变量采用了两种方法计算,这样就有8条收敛曲线。因为结构变量几乎不影响末端关节驱动系统变量,所以末端关节的驱动系统设计变量比其他关节收敛更快。 表6列出了驱动系统设计变量在两种方法中收敛的最优值和实验值。在两种方法中,驱动系统设计变量的收敛最优值几乎相同,如最优值16.24(A5,A6),这代表了最优值位于曲线上候选驱动系统A5和A6的额定力矩之间。 表6 驱动系统的设计变量最优值 将上述优化结果作为轻量化机械臂样机制作参数,由于所选的电机和驱动器所组成的驱动系统离散分布于拟合曲线。在曲线上力矩接近或者超过最优值的候选驱动系统被选为最优部件,这样能提供足够的功率以满足更大范围任务需求。因此候选驱动系统A6被选择为关节1的最优部件。 图10为机械臂的质量在两种方法中的收敛结果和在实验中的实际值。两种方法的收敛结果几乎相同,收敛的最优值分别为7.636 kg和7.583 kg。两种方法中机械臂的质量分别减轻了20.1%和20.7%。但是实验样机总质量是7.914 kg(比机械臂的初始质量减轻了17.2%),结果表明,使用驱动系统连续变量的统一优化设计能够实现全局优化并获得更轻的机械臂。且统一优化设计迭代14次就能收敛,能够提供更快的高效计算。 图10 机械臂的质量收敛图 基于优化结果制造了所设计的轻量化机械臂的实验样机,如图11所示。 图11 实验样机及测试过程 在测量中,实验样机运动轨迹与设计给定的运动轨迹相同,测量所得的实验力矩的RMS值分别为16.48 N·m, 19.12 N·m, 10.57 N·m和2.38 N·m。结果表明设计方法是有效的并且实验样机安全。而且,优化设计让4个关节的力矩RMS值分别减少了43.4%,34.3%,50.5%和79.6%。 此外,轻量化设计会使机械臂变得柔性;因此,末端执行器的变形量用来核查所设计的机械臂的刚度是否满足刚度约束条件。在本研究中,使用ICP加速度计(356A03)和数据采集仪来获得末端执行器的振动加速度。并且将测量的加速度数据在测试中被转化为位移,结果如图12所示。 图12 在局部坐标系{4}中的振动加速度A和位移D 图12(a)为在局部坐标系{4}中的振动加速度,图12(b)为利用积分运算将局部振动加速度变换得到的局部振动位移。全局振动位移变换公式如下: 0D=0T4(q)4D (15) 其中,0D=[0Dx,0Dy,0Dz]和4D=[4Dx,4Dy,4Dz]分别为全局和局部振动位移;0T4为同一变换矩阵;q为关节运动轨迹向量。 表7为局部坐标系{4}下和全局坐标系{0}下测量的最大振动位移。在局部坐标系中,振动位移最大值分别是0.528 5 mm,0.282 9 mm和0.218 4 mm。这些局部值转化为全局值分别为0.268 3 mm,0.151 4 mm和0.528 7 mm。因此,所有振动位移的最大值都小于优化中使用的最大允许变形量dmp=1 mm。结果表明所设计的轻量化机械臂的刚度满足刚度约束条件。 表7 在局部坐标系{4}和{0}坐标下测量点的最大振动位移 基于力矩密度曲线提出了一种新的机械臂轻量化方法,通过对机械臂的所有部件在质量上进行统一评估计算,能够快速计算获得最优设计结果。该优化结果被用来选择部件并试制了实验样机,实验结果表明了统一优化设计的有效性。2.2 设计条件和约束
2.3 目标函数
2.4 驱动系统参数的更新方法
2.5 优化过程和算法

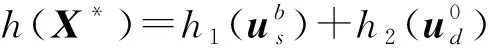
3 设计案例与实验
3.1 原理模型和设计条件

3.2 力矩密度曲线
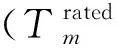

3.3 仿真结果讨论

3.4 实验结果和讨论

4 结论

