一种基于振幅物体约束的相位恢复算法

牟新刚,肖 靖,路志鹏

(武汉理工大学 机电工程学院,湖北 武汉 430070)

无透镜成像在实现大视场、高分辨成像有着独特的优势,同时无透镜成像凭借其系统简单、低成本和高通量的优点广泛应用于水质监测[1]、临床医疗[2]和细胞跟踪[3]等多个领域。但透镜引入了样本衍射重建的相位恢复问题。相位恢复算法主要分为非迭代算法和迭代算法两大类。

相移法、光强传输方程属于典型的非迭代相位恢复算法。前者利用光学相移硬件实现相位恢复;后者通过纵向振幅和横向相位的分布关系,利用多个记录振幅信息求解相位分布。光学器件本身尺寸限制了前者应用于样本邻接记录介质的无透镜成像系统。后者对拍摄图像质量要求较高,对衍射面噪声信息比较敏感,相比于迭代算法重建结果误差较高[4]。因此在计算成像中常应用迭代算法进行相位恢复。

迭代算法包括单帧迭代和多帧迭代算法。单帧迭代通过光场在物面支持域和像面振幅两个约束间来回迭代实现[5-6]。其主要应用于光源方向性较好的远场无透镜相干衍射成像系统中。近场无透镜相位恢复的多帧迭代原理基于多物距[7]、多波长[8-9]、多角度[10]以及叠层衍射成像[11-12]4大类,算法通过在不同距离轴向衍射面之间反复迭代得到最终收敛后的相位恢复结果。

笔者提出一种单帧迭代相位恢复算法,在传统GS(gerchberg saxton)迭代算法的基础上引入纯振幅物面约束,同时只需记录单帧强度衍射图像。通过样本物面与记录像面来回迭代传播,最终得到恢复相位后的衍射图以及消除孪生像后的重建样本图像。

1 相位恢复算法

光作为一种电磁波具有幅值和相位两种信息,图像频域的相位信息决定图像的空域分布。相位迭代恢复算法作为解决相位缺失问题的常用方法,在鲁棒性和相位恢复结果误差上是其他相位恢复算法很难达到的。

1.1 问题提出

常见的数字成像元件仅能检测光场的强度分布,无法感知高频变化的相位信息。

Urec=ASP-1{Uimg}=ASP-1{ASP(Utarget)}=Utarget

(1)

Uimg=ASP(Utarget,-z)=

(2)

式中:Urec为样本重建场分布;Uimg为衍射像场分布;ASP、ASP-1分别为角谱正向和逆向传播公式;Utarget为样本物光波场分布;z为物光场传播到像平面的距离;F,F-1分别为正向和逆向傅里叶变换;λ为物光波长;fx,fy为像场平面空间频率。

在图1所示的无透镜衍射系统中,平行光源穿过物体平面得到包含目标物体分布信息的物光波,物光波向前传播到记录平面上形成衍射图样。

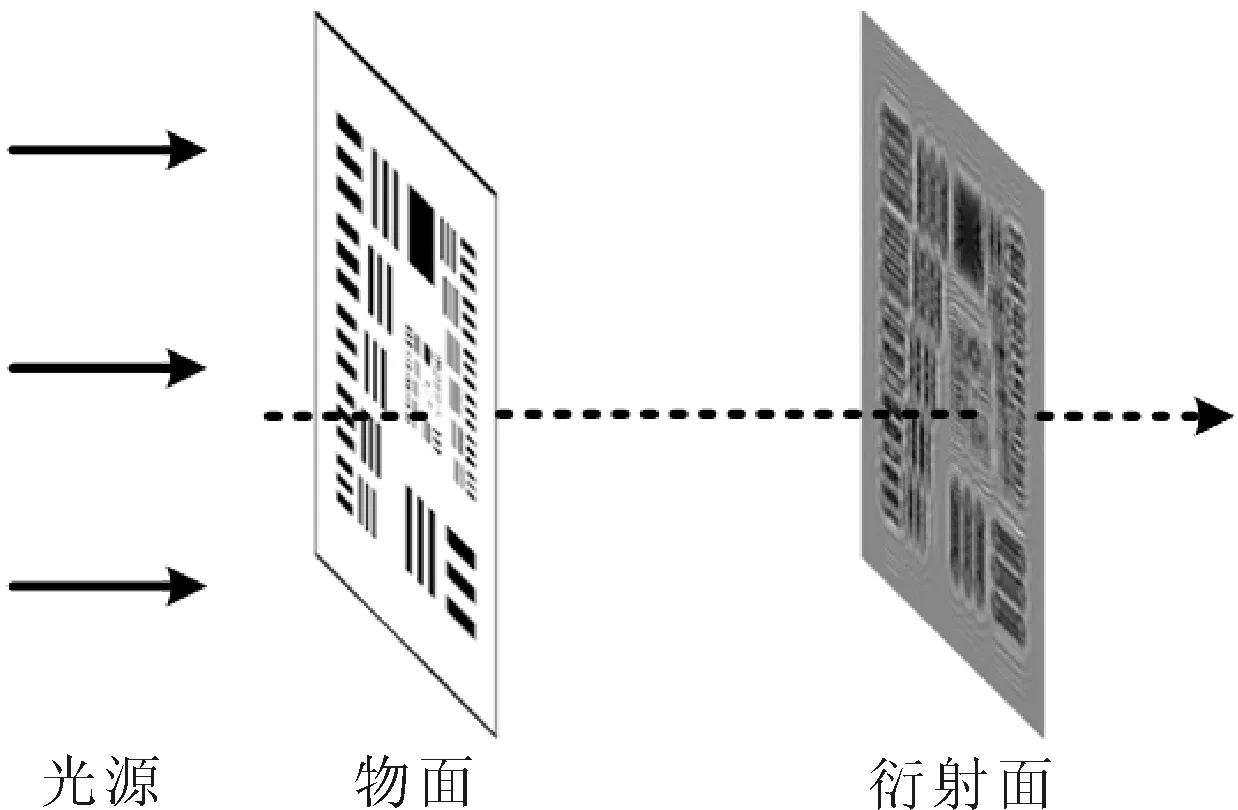
图1 无透镜衍射系统

记录介质在记录光场分布时存在局限性,即无法检测相位信息,只能测量光场的强度振幅信息。衍射像相位信息的缺失直接导致后续衍射重建结果出现大量共轭噪声,严重影响重建结果。图2为相位缺失的衍射像使用角谱法直接重建的结果,与原图相比存在大量纹路噪声,影响后续测量和观察。

图2 原始图像与重建图像对比

根据角谱衍射逆传播理论,如式(1)所示,当系统获取到包含相位信息的复振幅分布衍射图像Uimg,通过式(2)所示的角谱逆衍射传播重建算法可以重建无失真的样本图像Utarget。

1.2 迭代算法

笔者提出一种单帧迭代相位恢复算法。算法根据振幅物体零相位的特性建立物面相位约束,结合像面振幅约束在物、像两平面间来回迭代,最后得到相位恢复后的复振幅分布结果。

图3所示的流程图展示了算法的3个步骤:

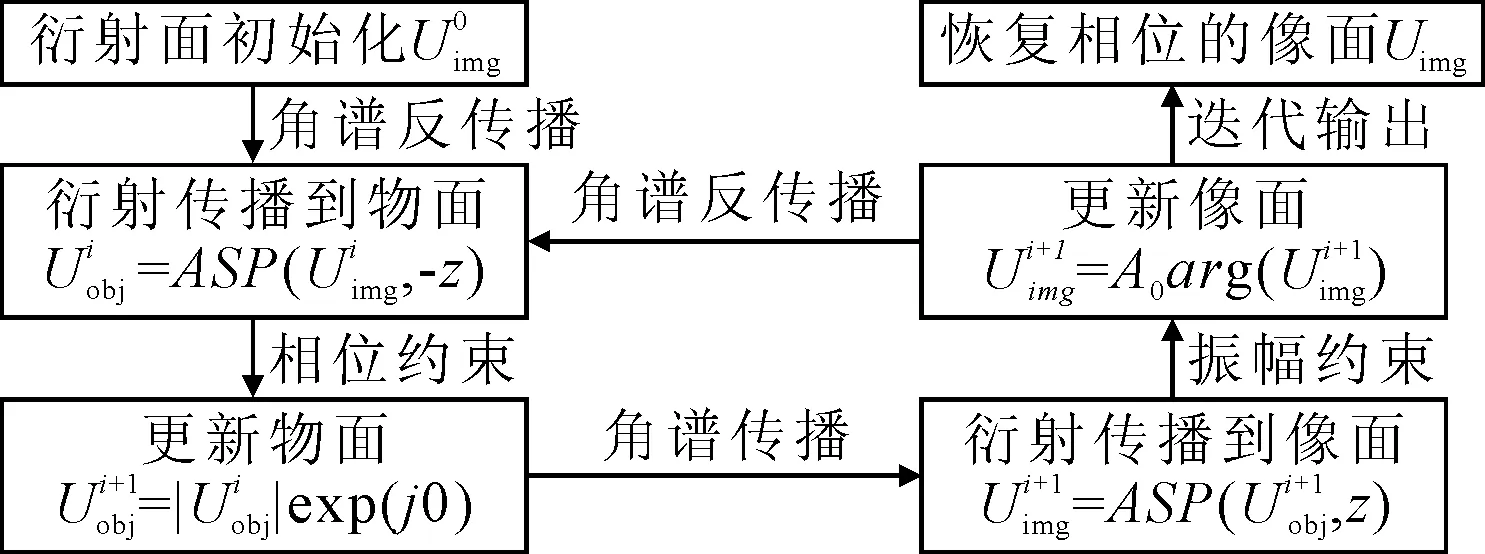
图3 单帧迭代相位恢复算法流程图

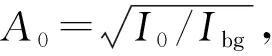
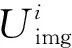
1.3 评价指标

衡量相位迭代恢复算法收敛效果可从像面和物面两个方面着手,其原理是相通的。为符合日常观察习惯,通过对比物面重建结果条纹可见度V对重建结果清晰度进行评价;选择重建结果与原图的均方误差MSE(mean squared error)衡量恢复算法结果噪声大小;实际应用时往往是样本原图未知,因此将已知的记录像面误差函数EF(error function)作为衡量算法重建效果指标。各指标计算表达式如下:

(3)

(4)

(5)

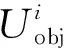
2 实验

2.1 实验条件

为验证算法的可行性,使用仿真系统生成衍射图像作为后续恢复算法输入。系统光源使用波长600 nm的平行光,为减少后续迭代算法运算量,此处选择图4(a)所示100×100像素的USAF(united srates air force)分辨率板作为样本观测对象。平行光经样本调制为物光波,角谱衍射传播物距z1=4 mm,z2=5 mm。到达尺寸100×100×3.75 um的记录平面,分别得到如图4(b)和图4(c)所示的衍射图像。

图4 原始样本图像与衍射振幅图像

2.2 实验结果

利用所提出的相位恢复算法对图4(b)所示的衍射图进行5 000次迭代相位恢复,得到样本的再现结果如图5(d)所示。为了评价该算法的性能,设置传统近场衍射GS算法和直接重建法作为对照组,GS算法通过在图4(b)和图4(c)两衍射面之间进行往复迭代运算,在5 000次迭代后得到如图5(c)所示的样本目标再现结果。直接重建法使用未经相位恢复的衍射记录图进行重建,图5(b)所示的重建结果为图4(b)衍射像直接角谱重建得到。图5(b)所示的直接重建结果受严重共轭噪声影响,噪声能量分布不均且大多以纹路的形式呈现,严重影响对目标的观察。与图5(a)的原始图相比,直接重建图像左下方区域部分线对已淹没在背景噪声中,因此无法通过阈值分割去除背景噪声。图5(c)所示GS迭代结果相比直接重接结果在噪声分布程度上有非常明显的优化,算法去除了大量共轭纹路噪声,但残留的随机噪声影响目标清晰度。图5(d)对应本文提出的恢复算法,消除了共轭噪声和随机噪声对观察目标的干扰,与图5(a)所示的原图一致。为衡量各算法重建结果对观测目标的影响,引入式(3)所示的条纹可见度V作为评价指标,对各重建结果的线扫描截面分布曲线图5(i)～图5(l)进行对比分析。

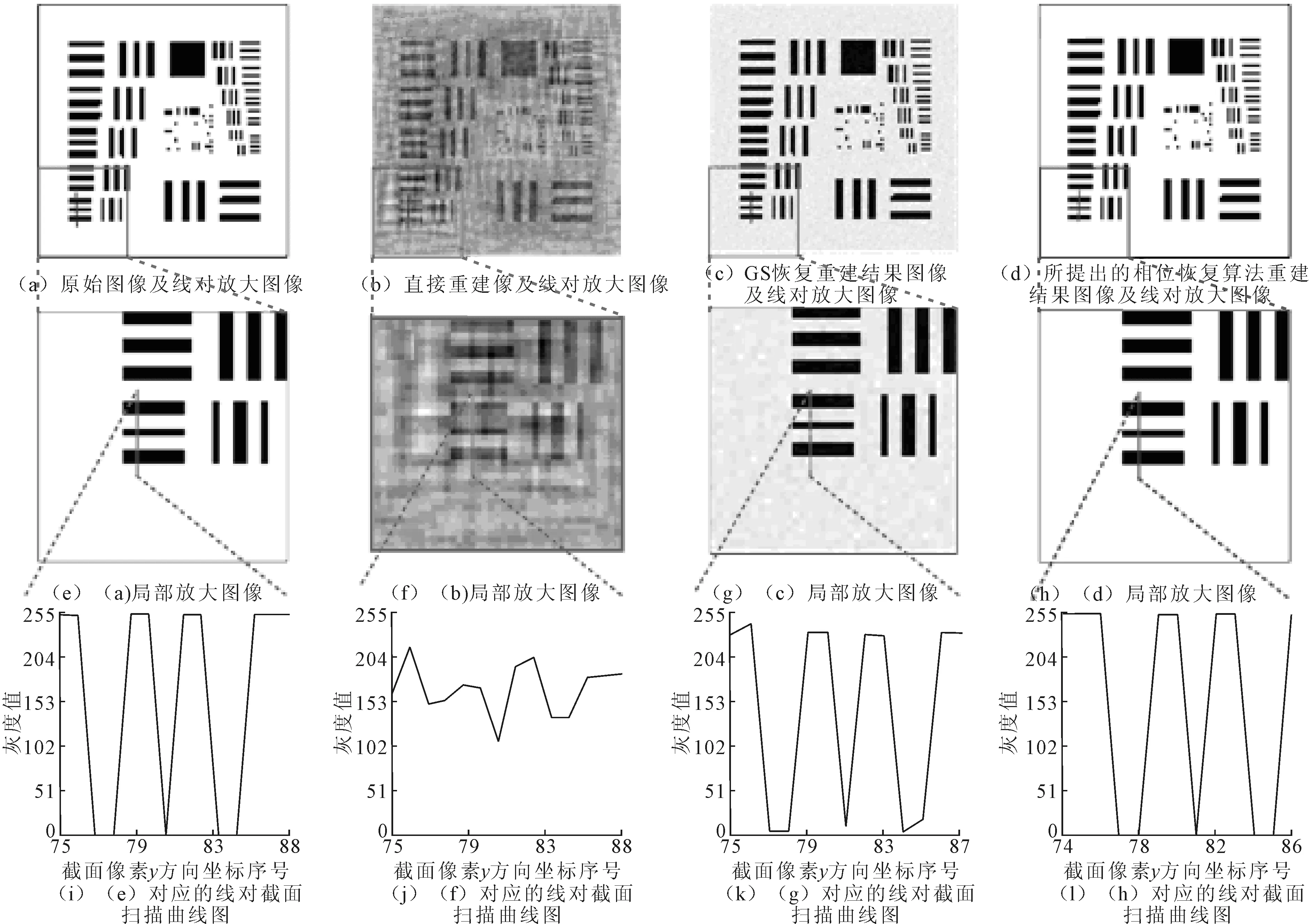
图5 样本各重建结果比对

图5(j)由于存在共轭背景噪声,直接重建结果由原来的峰峰值0～255变换成102～210,因此目标线对可见度为0.3,与可见度为1的原图相差较大。若实验选择观测对象为弱可见样本,将很难从重建结果中分辨出目标对象。图5(f)所示的GS算法对噪声抑制作用明显,而随机噪声的存在使得重建峰峰值为5～230,对应0.9的图像可见度,从图像上看目标线对很容易辨别。图5(d)所示的线扫描结果达到与原图相同的可见度,对应重建结果没有噪声干扰。图5(b)和图5(c)表明衍射像缺失的相位信息在物面以共轭纹路噪声和随机噪声的形式出现,其中属共轭噪声对目标的影响最为明显,如图5(j)所示。而所提出的相位恢复算法能有效抑制共轭噪声和随机噪声。

为进一步量化两种算法在迭代过程中的相位恢复效果,将从均方误差对相位恢复效果进行衡量。根据重建物面的形式可将重建结果与原图的均方误差分为振幅均方误差AMSE(amplitude mean squared error)和复振幅均方误差CMSE(complex amplitude mean squared error)。分别衡量重建结果与原图之间的振幅和相位误差。

图6(a)为物面振幅均方误差随迭代次数r的变化曲线,图6(b)则是复振幅均方差曲线。对比两曲线图可知复振幅均方误差始终大于振幅均方误差,满足实部虚部相加两边之和大于第三边的关系。首先,对比传统GS算法的两曲线图发现,振幅均方差随迭代次数增加呈递减趋势,代表迭代算法重建图像振幅分布随迭代次数增加越来越接近原图,从开始的0.017逐渐降到0.000 42,GS算法通过5 000次迭代将误差缩小了25倍,平均每200次迭代降低一倍误差;其中,误差从0.017下降到0.000 91经过419次迭代,平均每38次迭代降低一倍误差;从0.000 91下降到0.000 42经历4 581次迭代,平均每2 036次迭代降低一倍误差。前后迭代速度相差近一个数量级;由此可见GS算法的收敛速度越来越慢,419次迭代之后优化的效果不明显。同时注意到图6(b)中复振幅均方差曲线呈缓慢增长趋势,从开始的1.619到1.627缓慢增加,误差在236次迭代达到1.627后保持稳定不再变化。稳定的复振幅误差说明GS算法重建的样本与原图相比有稳定的相位偏差,同时逐渐减少的幅值误差说明重建样本在振幅上无限趋近原始图像。因此GS算法得到的结果为振幅上无限趋近但与原图相比有稳定相位偏差的复振幅重建像,且迭代收敛速度越来越慢,因此该算法适用于对振幅噪声和相位偏移要求不高的观测场合,由于笔者仅研究纯振幅样本,因此不考虑相位偏移。其次,对比所提出的算法两误差曲线图,观察比较振幅误差的迭代收敛速度发现,经过419次迭代后误差降低了33倍,平均每13次迭代缩小一倍误差;之后经过4 581次迭代误差降低了31 579倍,平均每次迭代缩小7倍误差;前后迭代速度相差91倍。因此该算法迭代速度随迭代次数的增加呈现增长趋势。同时图6(b)中复振幅误差也呈下降趋势,在迭代次数为2时出现一拐点,拐点前后复振幅误差与振幅误差比值由原来的47下降到1.1,在后续的迭代过程中再降低到1.001。与GS算法恒定复振幅误差不同,基于振幅条件约束算法可将重建图像的相位偏移降低到极小范围内。之后复振幅迭代误差的收敛速度与在振幅中的收敛速度一致,即在从2～5 000相同的迭代次数下,误差均下降了两个数量级,复振幅误差与振幅误差保持高度一致性。因此该算法适用于纯振幅物体这类无相位信息的目标。对比图6(a)中两算法曲线,两曲线在迭代次数为419处相交,角谱逆传播法求解此时两恢复算法的重建物像,如图7所示。

图6 迭代过程物面均方误差变化曲线

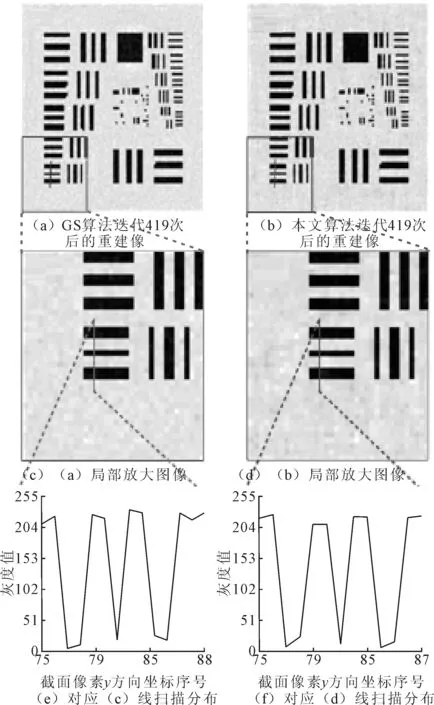
图7 相交点处两算法重建像比对

比较图7(a)和图7(b)所示的交点处两迭代算法重建像可知,本文算法重建像相比图5(b)所示的直接重建像,在图像噪声上有很大改善,大量有规律的共轭噪声被去除,为衡量两算法额外引入的随机噪声,对比两重建像的线扫描结果曲线如图7(e)和图7(f)所示。两重建像的强度能量均在5～225范围内,因此两重建像可见度V均为0.96,说明从视觉观察角度两重建像的效果是相同的。结合图6(a)可知两重建像在误差水平上也一致,因此可得两重建像线相交处的平均迭代收敛速度一致,而在此之前GS算法迭代收敛速度要高一些,在这之后所提出的算法迭代速度要快一些。因此当迭代次数小于419次时,GS迭代算法迭代速度比所提出的算法快1.6倍;而在迭代次数大于419次时,本文算法比GS迭代算法快一个多数量级。

在实际实验中,往往不能准确得到物光场的复振幅分布,因此以上两个评价指标多用于仿真分析,实际实验常用误差函数EF来衡量相位恢复算法结果误差。

误差函数EF用于衡量迭代过程的衍射像与记录得到的衍射像之间的误差。迭代过程EF误差曲线如图8所示。对比图6(a)和图8可知,两种算法的两类误差曲线在变化趋势上一致。且由于误差函数EF未做平均化处理,因此其误差值稍微偏高,将其除以像素数100×100后进行比较,在1～5 000次迭代过程中,GS算法EF误差下降11倍,与AMSE误差下降25倍的相差较大。

图8 迭代过程EF随迭代次数r变化曲线

本文算法EF误差每迭代一次下降3倍,与AMSE误差每迭代一次下降243倍的相差也较大。在相交节点处迭代次数不一样。在开始迭代时,GS算法的AMSE误差是EF误差的3.6倍;本文算法的AMSE误差是EF误差的7倍。5 000次迭代后AMSE误差是EF误差的883倍;本文算法的AMSE误差是EF误差的9 410倍。虽然两变化曲线不构成线性关系,但随着迭代次数的增加,EF衍射面误差迭代收敛速度比实际物面迭代收敛速度慢2～81倍,可以作为迭代收敛条件近似描述物面收敛情况。

3 结论

笔者提出一种基于振幅样本的相位恢复算法,通过仿真实验对算法有效性进行验证。仿真实验重建结果表明,引入振幅约束可有效提升相位恢复质量,消除物面共轭噪声和随机噪声。此外,通过像面误差评价指标误差函数的变化曲线发现,引入振幅约束可有效提升相位恢复算法迭代收敛速度,且在与传统近场衍射GS算法的对比实验中,相比多个衍射面的记录振幅约束,引入物面振幅约束条件的迭代结果很好地收敛到原始图像,而传统算法在收敛速度随迭代次数的增加愈发缓慢,存在迭代极限,而所提出的算法在迭代后期一直保持极高的收敛速度。因此所提出的算法能有效提升振幅样本的迭代收敛速度以及重建结果的准确性。为振幅物体的衍射成像提供了新的途径。