基于分子动力学的P(VDF50-TrFE50)高电场极化仿真

余 震,胡 柯,秦庆平,任豪豪

(1. 武汉科技大学冶金装备及其控制教育部重点实验室,湖北 武汉,430081;2. 武汉科技大学机械传动与制造工程湖北省重点实验室,湖北 武汉,430081;3. 通标标准技术服务(青岛)有限公司,山东 青岛,266101)

柔性压电传感器在可穿戴式智能装备中应用广泛,其工作原理是基于压电材料的正压电效应。压电材料在外部激励(外电场或外力)下,内部的电偶极子受力矩作用而旋转,当大量电偶极子共同转向某一方向时,其相对的两个表面上同时产生符号相反的电荷;为了中和压电材料中的压电电位,外部自由电荷转移并集聚在电极上,此时两个表面间可检测出电势差波动;当外部激励撤去后,电荷反向流回,产生一个相反的电势差波动[1]。对于具有压电性能的聚合物,其分子结构中包含分子偶极子,且这些偶极子可以在主体材料内通过极化过程被重新定向并保持这种排列,从而具有正压电效应。聚合物基压电材料比无机材料能承受更大的应力,并且可以应用于大面积传感器,但与压电陶瓷和单晶材料相比,聚合物基压电材料的居里温度和压电系数较低,这又限制了其应用[2-3]。

常见的聚合物基压电材料有聚偏氟乙烯(PVDF)、聚氯乙烯(PVC)、聚乳酸(PLLA)和聚酰胺(PA)等,其中,PVDF及其共聚物是具有最高介电常数和最佳全方位电活性的聚合物家族[4]。PVDF是一种半结晶材料,主要有5种不同的晶相,即α、β、γ、δ和ε相,其中β相聚合物链排列为全反式(平面锯齿形)构象[5],其压电性能相对更好。但PVDF在合成后都是非极性的α相,需要通过复杂的处理转化为β相。结晶相并非是影响PVDF压电性能的唯一因素,Cauda等[6]发现,尺寸限制和定向结晶都是决定PVDF压电性能的关键因素。研究人员还发现,将三氟乙烯(TrFE)引入PVDF的碳链产生出新的聚合物P(VDF-TrFE),其倾向于结晶成类似PVDF的β相晶体结构,因而具有很好的压电性能[7],这大为简化了电活性聚合物薄膜的制造过程。尽管如此,P(VDF-TrFE)还是必须通过电场极化,使得其所有域对齐以实现最大的宏观极化[8]。

PVDF的极化方法有多种,如高电场极化[8]、电晕放电极化[5]或通过掺杂铁氧体、钙钛矿等材料[9]以获得较高剩余极化。高电场极化是研究PVDF 传感特性的主要方法,其前提是设计合理的极化电场强度。另外,在开展铁电聚合物试验研究之前,从机理上探索其传感特性是十分必要的。Bystrov等[10]基于量子力学和分子力学方法,计算出PVDF的d33值,并发现了磁场对PVDF分子链长度的影响规律。You等[11]指出PVDF及其共聚物通过弱范德华相互作用凝结并显示出负压电性,然后通过密度泛函理论计算,揭示了一类二维铁电材料负压电性的根源。范德华相互作用与库仑力等均属于分子间作用力,分子动力学模拟有助于阐释PVDF基共聚物的优异压电性机理。

在P(VDF-TrFE)共聚物中,VDF含量在50%～80%时,共聚物表现出良好的剩余极化[12],且VDF和TrFE两种成分的物质量之比为50∶50的P(VDF50-TrFE50)薄膜具有最高的纵向压电响应[13]。Materials Studio (MS)是一款专门为材料学领域开发的计算模拟软件,可帮助研究者更方便地建立分子三维结构模型,并能对各种晶体/非晶体材料的性质及相关过程进行深入分析。因此,本文选取P(VDF50-TrFE50)为样本,利用MS软件建立三维晶胞模型,还原P(VDF50-TrFE50)分子偶极子的高电场极化全过程,探究各项极化条件对其剩余极化的影响,同时对MS在高分子压电材料模拟中的有效性进行验证,以期为更深入的仿真研究和后续试验研究奠定基础。

1 P(VDF50-TrFE50)晶胞模型构建与电场极化仿真验证

1.1 分子动力学模拟简介

分子动力学模拟[14-15]是一种计算物理学方法,主要用于模拟分子系统的动态进程和行为。其原理是将N个粒子构成的系统抽象成N个相互作用的质点,每个质点具有坐标、质量、电荷和成键方式。根据Boltzmann分布,按照目标温度随机指定各质点的初始速度,然后根据所选力场中的成键和非成键能量表达式对质点间的相互作用能以及每个质点所受的力进行计算,再基于经典牛顿力学原理计算系统中各质点的加速度及速度,经过指定的积分步数后得出运动轨迹,最后对轨迹或最终图像进行各种结构、能量及力学分析,得到所需计算结果。

在分子动力学模拟中,分子能量的表达式如式(1)和式(2)所示:

Etotal=Epotential+Ekinetic

(1)

Epotential=Evalence-diag+Evalence-cross+Enon-bond

(2)

式中:Etotal为总能量;Epotential为势能;Ekinetic为动能;Evalence-diag、Evalence-cross分别为键能对角项和交叉项;Enon-bond为非键能项,包括范德华力能、静电力能和氢键能。

在MS软件中以力场表示上述能量,本文选择CompassⅡ力场进行P(VDF50-TrFE50)分子动力学模拟。该力场具有极佳的精确性,可同时预测凝聚态和气态的性质,适用于模拟有机高分子、金属及金属氧化物等材料。

1.2 晶胞模型构建

由于P(VDF-TrFE)是二元共聚物,本文采用MS聚合物建模工具Random Copolymers建立P(VDF50-TrFE50)的单链模型,其聚合度为10,如图1(a)所示。在Amorphous Cell (AC)模块中选取CompassⅡ力场、NVT系综[16]和周期性边界条件(该条件用于消除尺寸效应的影响)建立密度为1.9 g/cm3的P(VDF50-TrFE50)无定形晶胞,选取10条P(VDF50-TrFE50)分子链,该模拟体系实际上是由基本单元(即晶胞)在各个方向上重叠而成,但在模拟中只须保留基本单元,所有其他单元与基本单元由平移对称性关联。

AC模块采用Monte Calro法建模。鉴于共聚物体系中重复单元的分布以及构象的分布存在大量不确定的情况,Monte Calro随机抽样法可提供一种模型搭建的思路,但随机方法无法保证初猜模型具有最低能量。在自然情况下,分子主要以能量最低的形式存在,故能量最低的构型才具有实际意义,其性质才能代表所研究的体系。因此需要将初猜模型优化到能量最低状态,优化方法为几何优化+退火算法。首先,选取Smart方法进行几何优化,计算质量选为Ultra-fine。该无定形晶胞包含200个C原子、250个F原子、170个H原子,总计620个原子。生成20帧无定形晶胞图像(图1(b)为第一帧),选取其中能量最低帧。然后,在Forcite模块中,通过退火算法、以给体系升温或降温的方式来降低其能量,筛选出稳定的结构。退火运算不会改变分子内成键方式,也不会使分子键断裂,退火次数越多,获得的结构也越多。结合机器算力,本文采用50次退火运算,在获得足够多晶胞构型的同时也能节约计算时间。选取能量最低帧为最终晶胞模型,如图1(c)所示,其总能量为-16.66 kJ/mol,晶格常数为1.856 65 nm,此时其Z轴方向的自发极化强度为3.228 mC/m2。

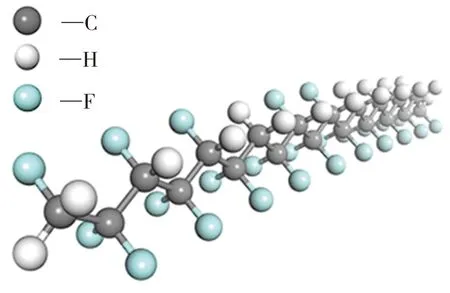
(a)聚合度为10的P(VDF50-TrFE50)单分子链模型

1.3 电场极化仿真验证

根据选取的晶胞模型,采用Materials Studio的Forcite模块进行极化仿真,并编写Perl语言脚本给晶胞施加外加电场。Furukawa等[17]研究发现,PVDF及其共聚物需要在极高的电场强度(GV/m级)下才能清晰地表现出其铁电性,因此这里将仿真电场强度设为2 GV/m(即2 V/nm),电场方向沿Z轴正向,用高电场强度下的极化仿真来检验本文方法。

Forcite模块设置中最重要的参数是力场和电荷,本文采用适用于有机分子的CompassⅡ力场、NVT系综;计算的原子电荷为:C原子电荷0.207e,F原子电荷-0.260e,H原子电荷0.053e。计算质量设定为Ultra-fine,运行Dynamic算法仿真,得到极化后的晶胞,如图2所示。在极高电场强度下,晶胞内分子排列发生了显著变化,P(VDF50-TrFE50)分子链中的H原子端有规律地朝向Z轴正向,而F原子端则有规律地朝向Z轴负向,这些现象清晰体现出P(VDF50-TrFE50)的铁电性。

(a)正视图

(b)正轴测图

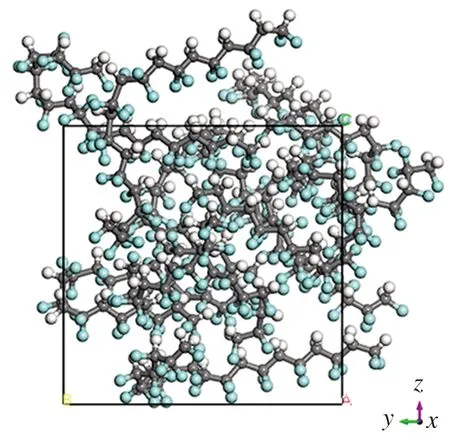
(c)左视图

P(VDF50-TrFE50)晶胞在温度为413 K、电场强度为2 V/nm条件下的极化曲线如图3所示。根据式(3)可将偶极矩矢量和换算为极化强度:

P=∑p/ΔV

(3)

式中:P为极化强度,C/m2;∑p为偶极矩矢量和,Debye(1 Debye=3.33564×10-30C·m);ΔV为晶胞体积,m3。

理论上共聚物在极高电场强度下的极化分为两个阶段[17],图3模拟结果与此相符:第一阶段,晶胞内铁电畴在短时间(10 ps)内快速翻转,也称快速极化;第二阶段,极化强度缓慢增加,此时的极化强度来源于位移极化。以上研究结果初步验证了本文仿真方法的有效性。

图3 P(VDF50-TrFE50) 晶胞在413 K、2 V/nm条件下的极化曲线

2 P(VDF50-TrFE50)晶胞电场极化仿真与结果分析

2.1 极化仿真时间参数的确定

在1.3节的仿真验证中,极高电场强度情况下晶胞在10 ps (即104步)内便完成了铁电畴快速翻转,而仿真试验总共进行了500 ps (即5×105步),花费了大量的计算时间。因此本节对极化时间与极化强度的关系进行研究,为后续极化仿真试验制定合理的时间参数,以便在得到准确结果的前提下还能节约计算时间。

首先,对晶胞在较低电场强度下的快速极化阶段进行仿真试验,确定此条件下的仿真时间参数。极化温度设为413 K、电场强度设为0.3 V/nm,对P(VDF50-TrFE50)晶胞进行1 ns(步长为1 fs,共计106步)的极化仿真,通过一次时长足够的仿真确定适宜的仿真时间(步数)。结果表明,晶胞的快速极化阶段为20 ps,在100 ps内达到最大极化强度,在300 ps内达到稳态,如图4所示。因此可取前100 ps内偶极矩矢量和的极大值计算最大极化强度。

图4 P(VDF50-TrFE50)晶胞在413 K、0.3 V/nm条件下的极化曲线

其次,对晶胞在高电场强度下的快速极化阶段进行仿真试验,确定此条件下的仿真时间参数。鉴于NVT恒温系综对温度的优异控制(如图5所示),可以不考虑P(VDF50-TrFE50)被电击穿、炭化的情况,从而可设置极高的电场强度。在其他参数保持不变时,将电场强度增加为3 V/nm,进行300 ps (3×105步)的分子动力学仿真,以确定仿真时间下限。仿真结果如图6所示,和电场强度为2 V/nm时的情况一样,在10 ps左右,P(VDF50-TrFE50)晶胞的Z轴正向铁电畴已充分对齐,然后偶极矩矢量和缓慢增长,在100 ps后保持稳定。由此可知,当电场强度高于2 V/nm时,P(VDF50-TrFE50)晶胞的快速极化阶段不短于10 ps。

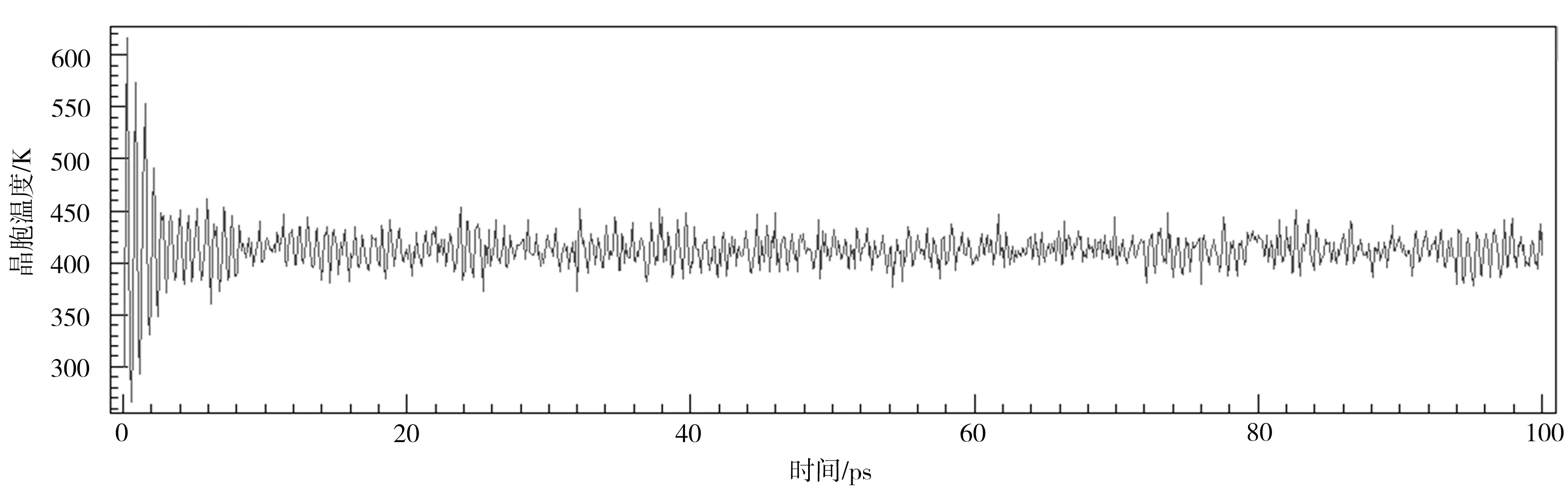
图5 413 K时P(VDF50-TrFE50)晶胞极化的温控曲线

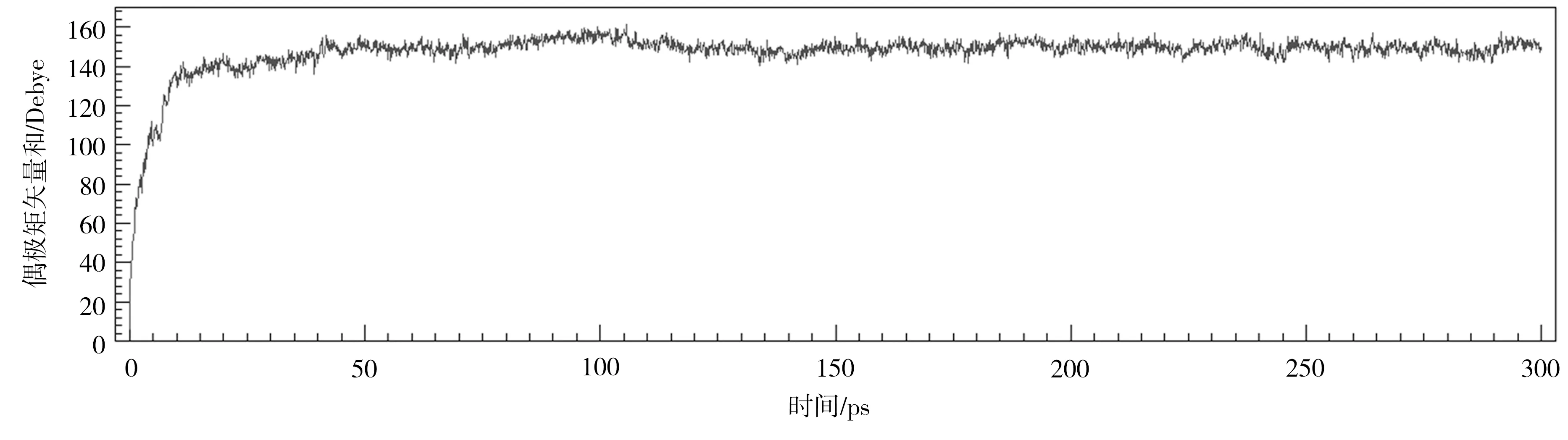
图6 P(VDF50-TrFE50)晶胞在413 K、3 V/nm条件下的极化曲线

综合考虑,为了得出准确的仿真结果并且节约计算时间,当电场强度小于2 V/nm时,仿真时间应在100～300 ps之间;当电场强度大于2 V/nm时,仿真时间应在10～100 ps之间。

2.2 电场强度对极化强度的影响

实际中P(VDF-TrFE)的极化常在333～413K条件下进行[18],本节仿真研究首先考察P(VDF50-TrFE50)晶胞由于分子热运动产生的自发极化现象。将极化温度设为413 K,在未施加电场时进行分子动力学模拟,结果如图7所示,可以看到P(VDF50-TrFE50)晶胞发生了热极化现象。然后保持极化温度为413 K,使用Perl语言脚本将电场方向设为Z轴正向,电场强度设为0.25 V/nm,进行100 ps的分子动力学模拟,结果如图8所示,可以看到,P(VDF50-TrFE50)晶胞在该条件下的极化强度不高于分子热运动产生的极化强度。

鉴于在电场强度小于0.25 V/nm的情况下,P(VDF50-TrFE50)晶胞未见明显极化现象,因此继续在电场强度为0.25～9 V/ nm时进行极化仿真,不同电场强度下的Z轴方向偶极矩矢量和与仿真时间的关系如图9所示。P(VDF50-TrFE50)晶胞极化时,外加电场强度与最大偶极矩矢量和的关系如图10所示。当电场强度小于2 V/nm时,取图9对应极化曲线中偶极矩矢量和的极大值作为图10纵坐标值;当电场强度大于2 V/nm时,取图9对应极化曲线后10 ps的偶极矩矢量和平均值作为图10纵坐标值。

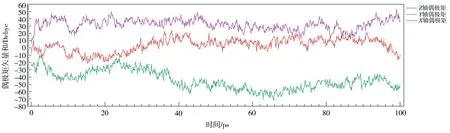
图7 未施加电场时P(VDF50-TrFE50)晶胞在413 K下的极化曲线

图10 电场强度与最大偶极矩矢量和的关系

由图10可知,P(VDF50-TrFE50)晶胞的极化强度与外加电场强度正相关,但当电场强度高于5 V/nm后,晶胞极化强度增长减缓。推测其原因是晶胞内部的分子偶极子已普遍对齐,此时的极化强度增量是由位移极化造成的。另外,在电场强度较低时,极化曲线并不平滑,这是由于电场力不足以使铁电畴克服晶体-非晶体相互作用,铁电畴无法对齐。

2.3 极化温度对极化过程的影响

为排除电场强度较低对P(VDF50-TrFE50)晶胞极化的不利影响,突显温度对极化过程的作用,本节仿真取较高的电场强度值。在10 V/nm的电场强度下,设置温度变化区间为298～473 K,进行100 ps的极化模拟,结果如图11所示。在4个温度值下,P(VDF50-TrFE50)晶胞均在1 ps左右达到最高极化强度的50%,并且最大偶极矩矢量和均在180～190 Debye(即极化强度93.8～99.0 mC/m2)之间。因此可以得出,极化温度与极化速率、极化温度与最高极化强度均没有明显的相关性,此时电场对偶极子的做功远大于该温度下分子的能量,无法使晶胞的偶极矩矢量和进一步增加。

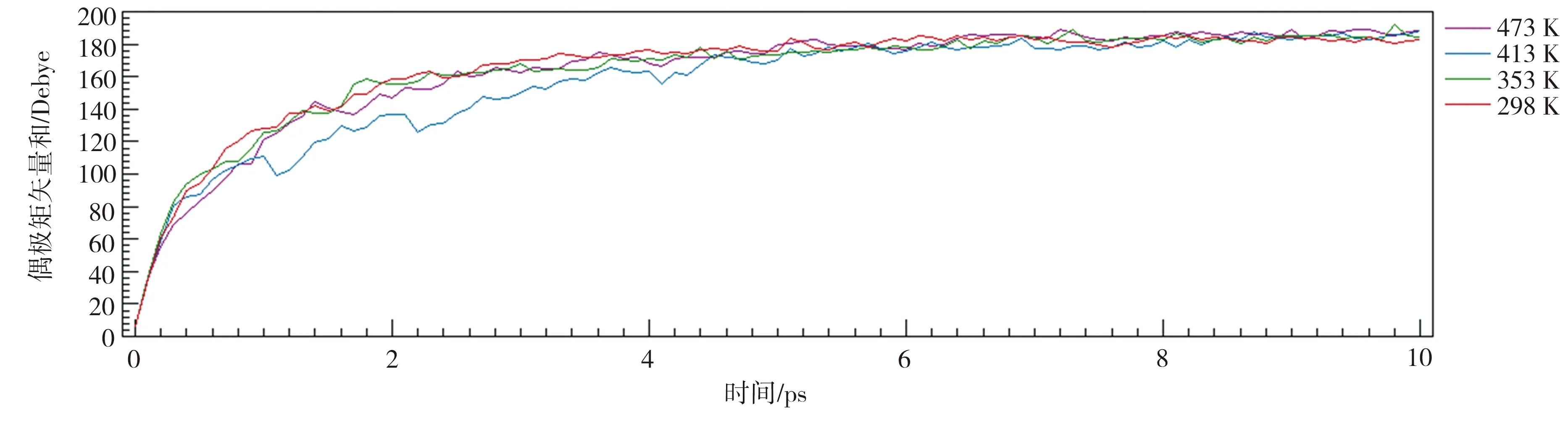
图11 P(VDF50-TrFE50)晶胞在10 V/nm、298～473 K条件下的极化曲线

3 P(VDF50-TrFE50)剩余极化仿真及结果分析

撤去被高电场极化之晶胞的外加电场后进行分子动力学计算,分析晶胞的剩余极化情况。选取轨迹文件中的偶极矩最大帧,输出为模型文件,对模型中的晶胞进行MS模拟。采用Forcite模块的Dynamic算法,选择CompassⅡ力场和Noes-Hoover控温方法,在不同温度下进行仿真计算,分两种情况对剩余极化进行讨论。

1)同一电场强度极化的P(VDF50-TrFE50)在不同温度下的剩余极化

首先在温度413 K、电场强度10 V/nm条件下进行P(VDF50-TrFE50)极化,仿真时间为100 ps,使其内部铁电畴充分对齐,此时晶胞如图12所示。然后撤去电场,在不同温度下进行分子动力学模拟,得到P(VDF50-TrFE50)的偶极矩矢量和,结果见图13。由图13可以看到, P(VDF50-TrFE50)晶胞在298 K和305 K的剩余偶极矩矢量和为100～120 Debye,即剩余极化强度为52～62 mC/m2,该结果与文献[17]报道的P(VDF-TrFE)剩余极化强度(见图14)基本相符。另外,在398 K的剩余极化归零,表示该温度下的晶胞由铁电相转变为顺电相,这与文献[17]指出的不同条件下P(VDF-TrFE)居里温度在353～413 K之间也相符。

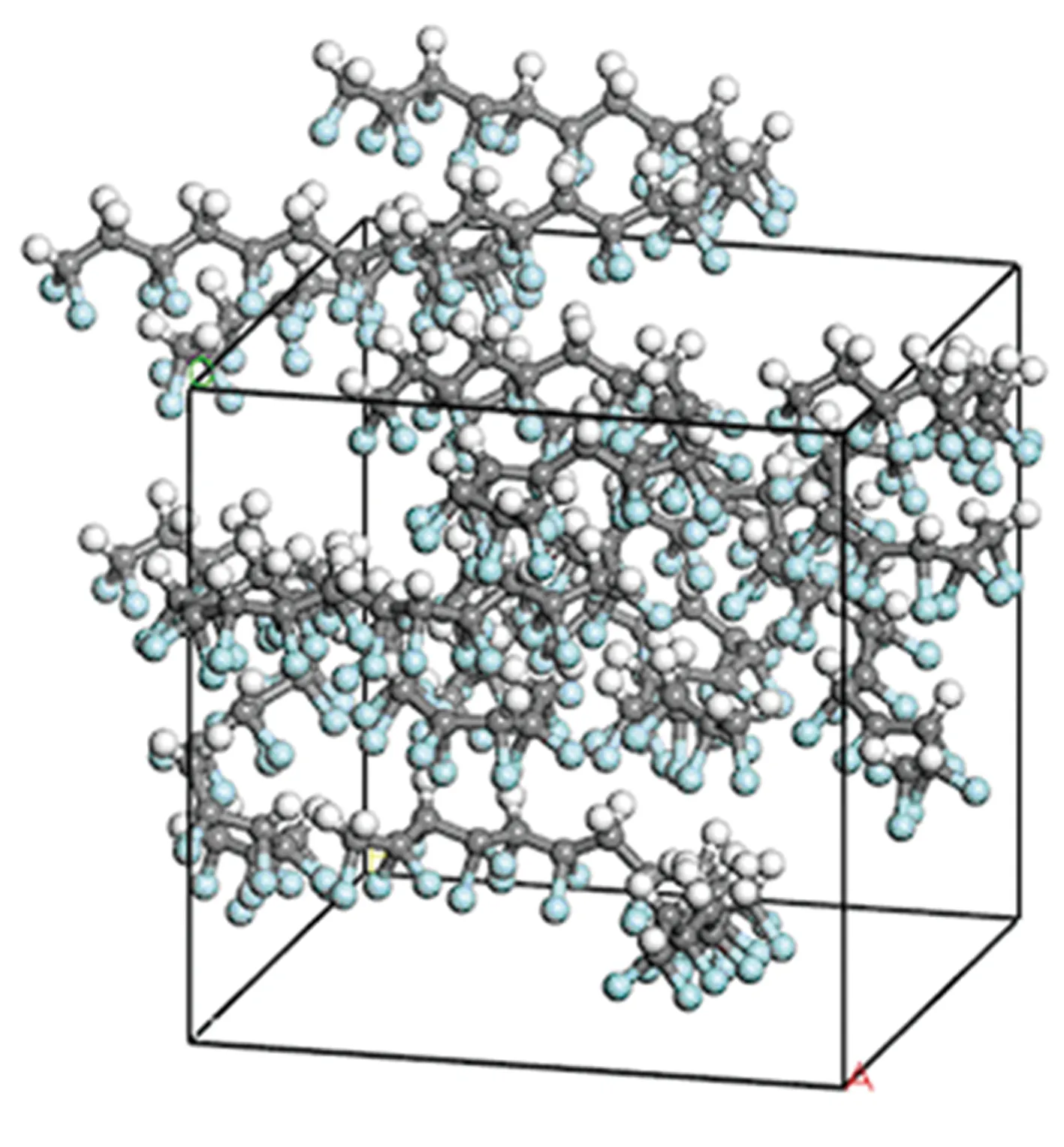
图12 P(VDF50-TrFE50)在10 V/nm电场强度下分子偶极子充分对齐的图像

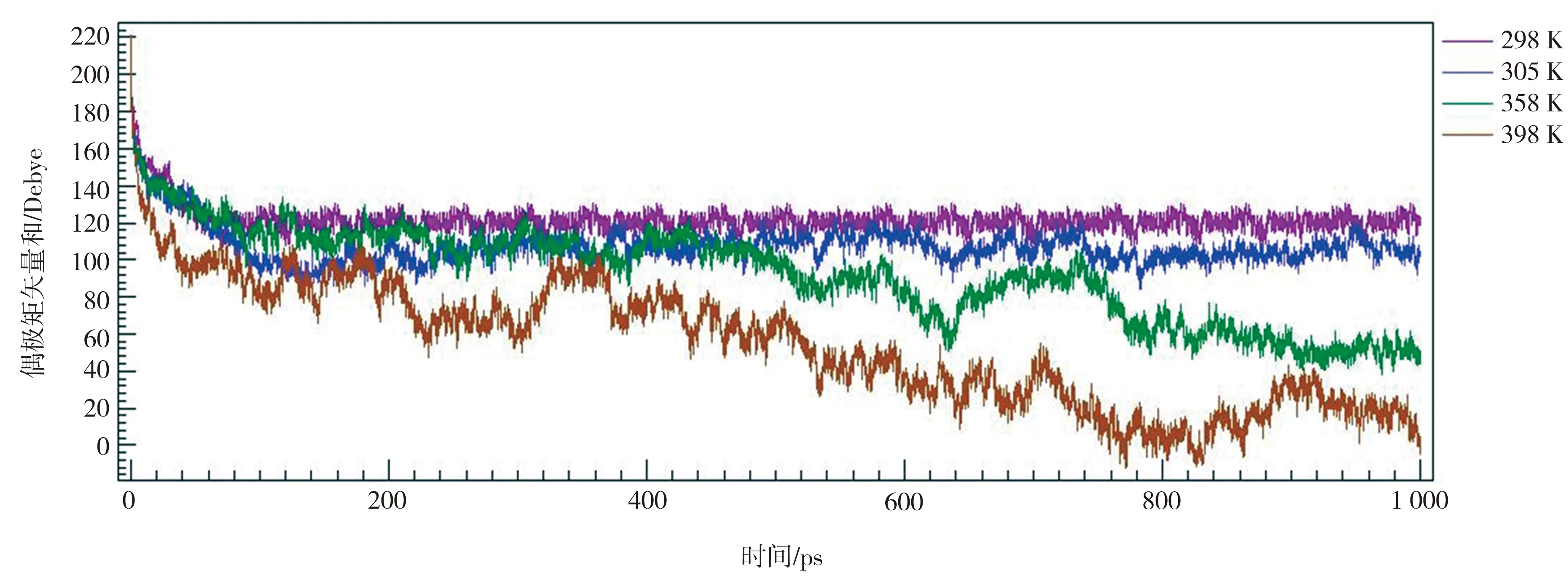
图13 P(VDF50-TrFE50)晶胞在不同温度下的剩余极化曲线

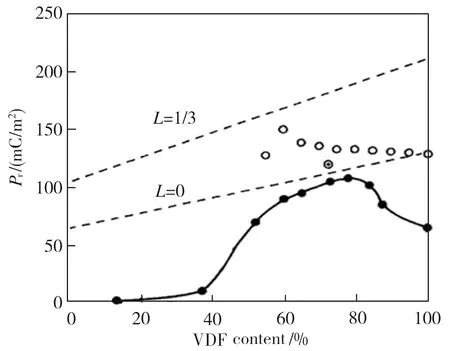
图14 VDF含量与P(VDF-TrFE)剩余极化强度之间的关系[17]

2)不同电场强度极化的P(VDF50-TrFE50)在相同温度下的剩余极化

首先在298 K和2～15 V/nm电场强度下对晶胞进行极化,确保晶胞内的铁电畴充分对齐至Z轴方向,然后撤去电场进行分子动力学仿真,结果如图15所示。在电场撤离后,大量极化对齐的分子偶极子在1 ps内产生随机翻转,P(VDF50-TrFE50)极化强度大幅下降,然后则缓慢降低。同时,由于部分分子偶极子被电场充分固定,因此在相同温度下,极化场强越高,晶胞的剩余极化强度也越高。将MS仿真后10 ps的数据取平均值,得出极化场强与剩余偶极矩矢量和的关系,如图16所示。

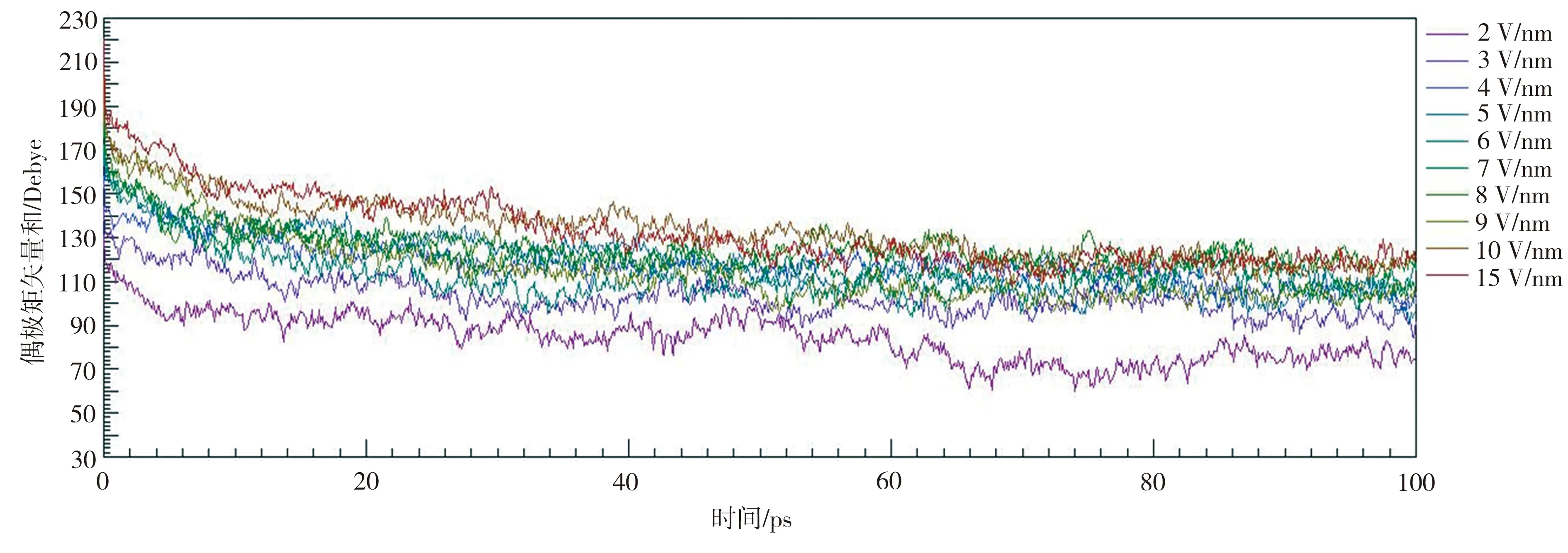
图15 在298 K和2～15 V/nm条件下极化的P(VDF50-TrFE50)晶胞的剩余极化曲线

根据两种情况的仿真结果,可以得出以下结论:

1)P(VDF50-TrFE50)的剩余极化与环境温度相关,为获得具有较高剩余极化强度的P(VDF-TrFE)薄膜,实验中应采用冷却装置将极化完成的P(VDF-TrFE)薄膜冷却至居里温度以下。

2)仿真得到的晶胞偶极矩矢量和与电场强度的关系曲线符合ExpAssoc分布模型。拟合曲线见式(4),决定系数r2为0.993。

∑p=6.193+25.144[1-exp(-E/8.556)]+

92.067[1-exp(-E/1.585]

(4)

式中:E为电场强度,V/nm。

3)当外加电场强度极高时,无论P(VDF50-TrFE50) 的最高极化强度有多大,其剩余偶极矩矢量和都将下降到115 Debye附近,即25 ℃下剩余极化强度约为59.94 mC/m2。

4 结语

本文在分析P(VDF50-TrFE50)的压电特性前提下采用MS分子动力学仿真软件对其高电场极化过程进行了仿真研究。

首先通过分子动力学仿真直观地展示出P(VDF50-TrFE50)内部偶极子在外电场作用下F原子和H原子绕C链旋转而发生的铁电畴对齐现象。P(VDF50-TrFE50)晶胞存在自发极化,且在高电场极化过程中显示出铁电畴翻转和位移极化两个阶段。

然后研究了极化过程中时间、温度和电场强度这3个条件对P(VDF50-TrFE50)极化强度的影响。P(VDF50-TrFE50)晶胞的极化强度与外加电场强度正相关,但当电场强度高于5 V/nm后,晶胞极化强度增长减缓。极化温度与极化速率、极化温度与最高极化强度均没有明显的相关性。

最后研究了晶胞剩余极化与外加电场强度、温度等因素的相互关系。温度的变化显著影响晶胞的剩余极化强度,晶胞在居里温度以上时存在失极化的现象;P(VDF50-TrFE50)聚合物在25 ℃下理论最高剩余极化强度约为59.94 mC/m2。仿真结果与文献[17]中报道的实验结果相符合,验证了基于分子动力学原理的MS软件模拟P(VDF-TrFE)材料铁电性能的能力。

本文结论可用于指导铁电相PVDF及其共聚物的d3i参数模拟研究方法的制定,并为后续试验研究及P(VDF50-TrFE50)材料的工程应用提供理论参考。