土石坝防渗墙抗水力劈裂特性研究

黎志源

(淮安市水利规划设计研究院有限公司广州分公司，广东 广州 510610)

伴随我国水利水电工程的快速发展，水库大坝对于经济社会的发展起到了不可替代的作用。土石坝由于取材方便及适应地形能力强的特点，被广泛应用于我国的水利建设。目前我国的土石坝已成为主要坝型，占比高达95%。但由于设计及施工缺陷，土石坝稳定性仍然是制约大坝安全运营的主要因素之一。其中坝体防渗墙水力劈裂问题就是影响大坝安全运营的重要因素之一。由于土石坝防渗墙水力劈裂可能会导致严重的后果，各国学者也对土石坝的水力劈裂问题开展了广泛的研究。殷宗泽等[1]对比分析了有效应力法和总应力法对于心墙堆石坝的水力劈裂计算结果的差异性，结果表明，防渗墙渗透性、饱和度及库水位上升速度等均会对水力劈裂产生影响。宁保辉等[2]基于数值模拟系统的研究了前坪水库大坝应力变形及抗水力劈裂响应。结果表明，坝体应力和变形分布符合一般规律，坝体最大竖向沉降发生在1/2～2/3坝高范围内，实际工程中，在大坝易出现裂缝部位可采取填筑高塑性土等工程措施防治渗流破坏。张红日等[3]基于二维数值模拟系统的研究了心墙水力劈裂与孔压关系。结果表明，坝体竣工期的拱效应，导致心墙竖向应力明显减小。此外，此压力梯度是水力劈裂发生的根本条件。魏松等[4]基于数值模拟分析了防渗心墙的拱效应及抗水力劈裂性能。研究结果表明，无廊道坝和有廊道坝的心墙内中主应力基本均大于或接近上游水压力。与无廊道相比，有廊道方案的混凝土防渗墙应力较大。实际工程中，提高覆盖层厚度模量可以有效降低防渗墙的变形。郭德全等[5]依托瀑布沟高土石坝工程，采用邓肯E-ν模型研究了高土石坝坝体和基础防渗墙在施工期和蓄水期的应力、变形分布规律，结果表明，大坝最大沉降均发生在水库满蓄期。此外，设置的高塑性黏土区改善了大坝的应力状况。邓建伟等[6]基于理论手段分析了沥青混凝土心墙坝水力劈裂发生机理。结果表明，沥青混凝土的低透水性是发生水力劈裂的重要物质条件。

既有研究中大多数没有考虑发生水力劈裂所需的前提条件，实际工程发现，防渗墙的裂缝特征对于水力劈裂效应是非常显著的。考虑目前的研究不足，本文依托某土石坝实际工程，采用ABAQUS建立理想均质土石坝模型，系统研究防渗墙裂缝特征及墙体的物理力学参数对水力劈裂的影响。本文的研究可为类似工程提供参考。

1 水力劈裂计算准则

防渗墙水力劈裂的时在水压力的作用下，主要是由于垂直裂缝面的拉应力和平行裂缝面的剪应力共同导致的。基于既有研究关于水力劈裂发生的条件[7-8]，本文提出了Ⅰ型和Ⅱ型裂缝的水力劈裂准则：

(1)

式中，KⅠ—Ⅰ型裂缝尖端的应力强度；KⅡ—Ⅱ型裂缝尖端的应力强度；KIC—材料的断裂韧度因子。

在上式中，当左端小于右端时，通常认为不发生水力劈裂，当左端大于右端时，通常认为发生水力劈裂，其中上式的左端由下式得到

(2)

式中，J—平面应变积分项；E—材料的弹性模量；μ—材料的泊松比，对于非弹性问题，两者取切线弹性模量和切线泊松比。

通过以上的分析可知，J积分的值越大，越容易发生水力劈裂，因此本文分析中主要通过计算J积分的大小确定是否发生水力劈裂以及影响水力劈裂的因素。

2 数值计算模型与参数

本文依托某土石坝水利工程，该坝是以防洪为主，结合灌溉、供水，兼顾发电的水利工程。坝体上下游坡比均为1∶1.8。设计防洪标准为500年，校核洪水标准为2000年。坝顶高程为1925m，最大坝高为200m，顶宽为14m。根据土石坝典型断面建立数值计算模型(如图1所示)。其中坝长为735m，坝高200m。顶宽14m。假定土石坝为均质材料。数值计算中采用的本构模型为邓肯-张模型。为了分析裂缝特征对水力劈裂的影响。本文假定防渗墙存在3条裂缝，由下到上分别定义为L1，L2和L3。其中L1距离坝底40m，L2距离坝顶100m，L3距离坝底160m。为了计算简便，本文不考虑裂缝产生的原因。此外，假定水位正常情况为180m，最大水位值为200m。模型约束条件为，约束左右两侧水平方向的位移，约束底部3个方向的位移。

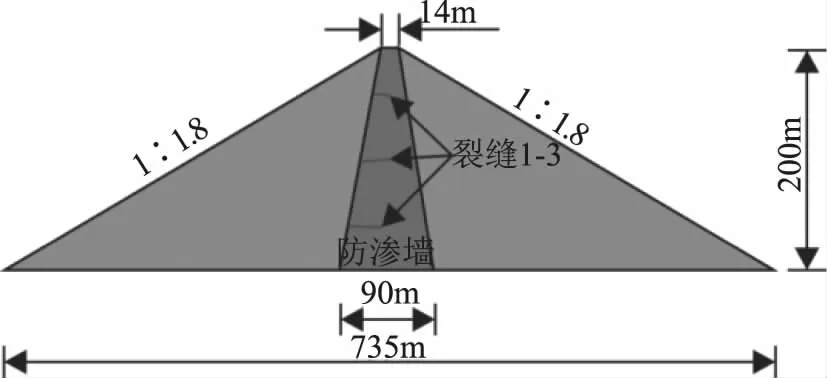
图1 数值计算模型

计算过程中，假定水位上升时瞬时的。此外，由于裂缝是假定直接存在于防渗墙上的，因此，假定蓄水时裂缝已经存，且裂缝弹性模量假定为大坝弹性模量的0.01%，泊松比为0.3。

3 计算结果与分析

3.1 水位对水力劈裂的影响

图2汇总得到了库水位对水力劈裂的影响关系。结果表明，J积分值的大小随水位的增大而增大，且两者呈比较明显的线性关系。在相同水位工况下，J积分数值的大小，随裂缝长度的增大而增大。也即在确定水位下，水位越高，越容易发生水力劈裂。此外，当裂缝长度为2.0m，J积分的数值大小基本不受水位高低的影响。因此可以发现，裂缝长度越大，受水位的影响也越大。实际工程中，如果裂缝长度比较小时，即使在水位比较大的时候，也不容易发生水力劈裂。

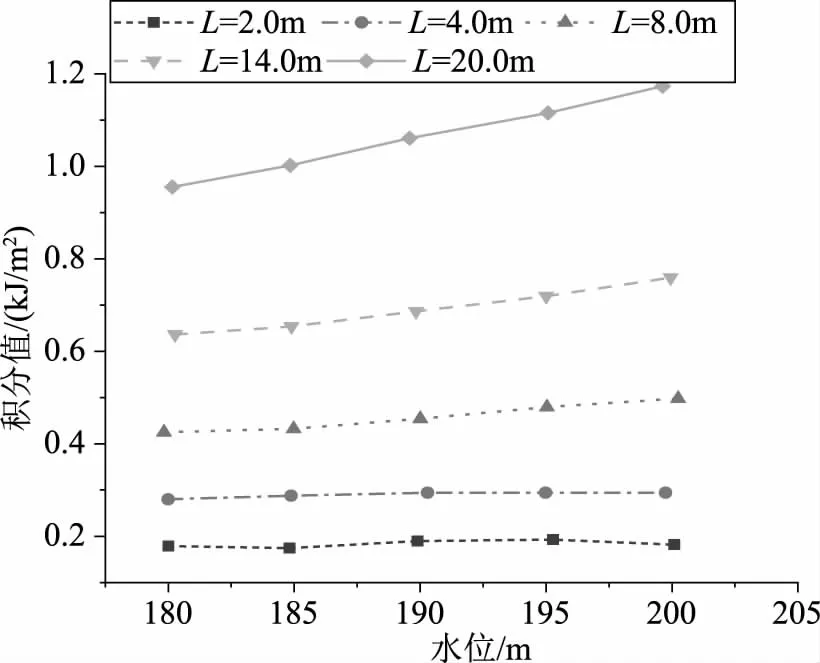
图2 库水位对水力劈裂的影响

3.2 裂缝长度水力劈裂的影响

图3汇总得到了裂缝长度对水力劈裂的影响。结果表明，在相同库水位情况下，J积分值的大小随裂缝长度的增大而增大。即对于确定的水位，裂缝长度越大，越容易发生水力劈裂。此外，在裂缝长度小于10m时，库水的波动对J积分的影响较小。证明，高库水发生水力劈裂的临界条件比低库水位发生水力劈裂的最小裂缝长度要小。

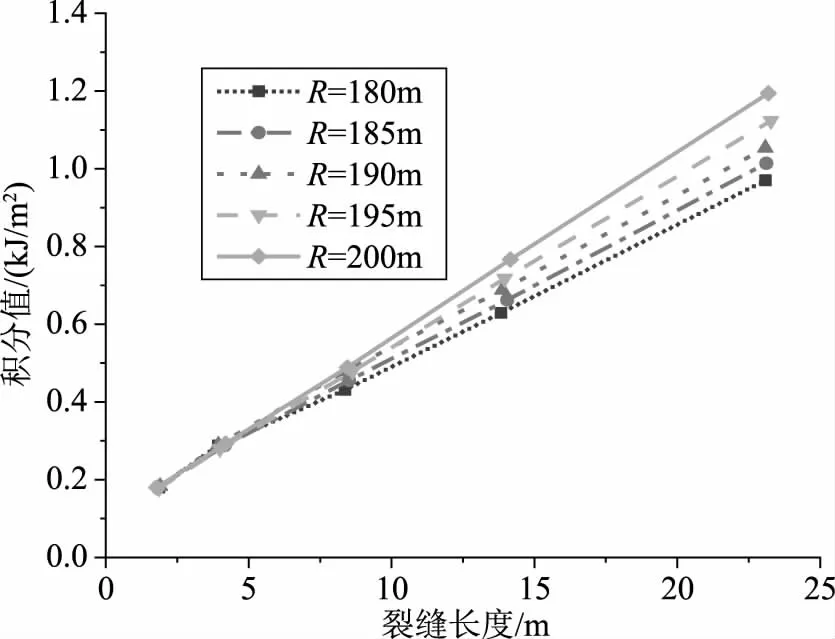
图3 裂缝长度对水力劈裂的影响

3.3 裂缝位置对水力劈裂的影响

既有研究表明，裂缝位置对水力劈裂的影响影响较大。通常外荷载作用下，裂缝往往出现在初始缺陷最严重的地方。裂缝时发生水力劈裂的基础条件。一些研究表明，最容易发生水力劈裂的位置是在坝体中上部。图4汇总得到裂缝位置对水力劈裂的影响。结果表明，相同裂缝长度下，J积分的大小与水位呈正相关的关系。在水位相同及裂缝长度相同的工况下，裂缝距离坝顶位置越小，越容易发生水力劈裂。

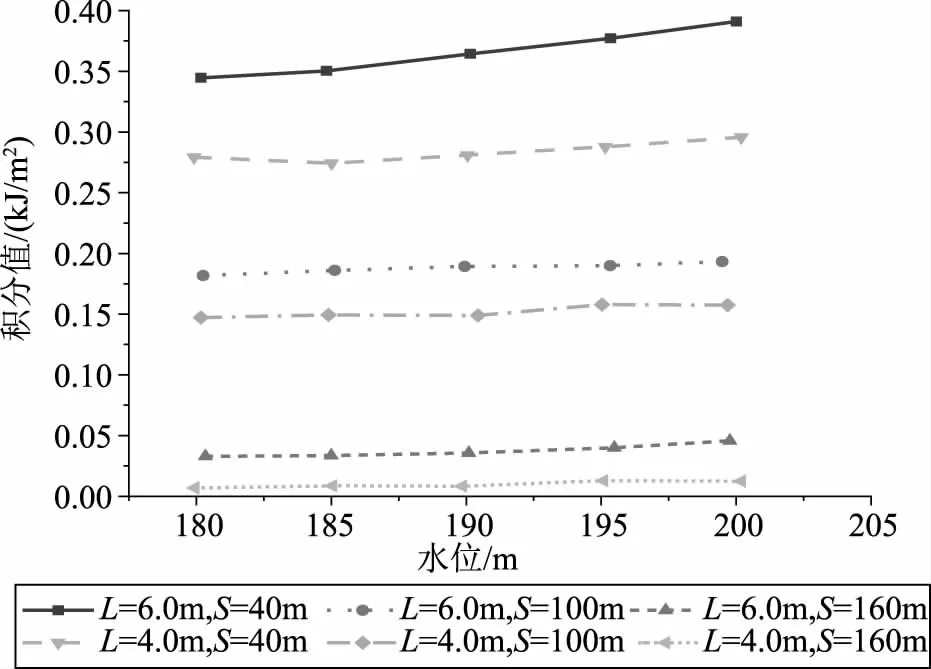
图4 裂缝位置对水力劈裂的影响

3.4 防渗墙力学参数对水力劈裂的影响

通常防渗墙裂缝会对水力劈裂产生影响。此外，防渗墙本身的力学属性也会对水力劈裂发生的条件产生影响。为进一步研究防渗墙力学特性对水力劈裂的影响，本文系统的分析了防渗墙弹性模量、泊松比及密度对水力劈裂的影响。

图5得到了防渗墙弹性模量对水力劈裂的影响。结果表明，J积分的大小随防渗墙弹性模量的增大呈非线性增大。证明提高墙体的刚度有利于提高防渗墙的抗水力劈裂能力。此外，提高防渗墙的弹性模量能够显著提高发生水力劈裂的最低水位要求。

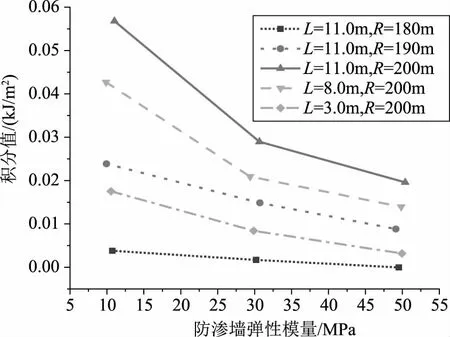
图5 防渗墙弹性模量对水力劈裂的影响

图6得到了防渗墙泊松比对水力劈裂的影响。结果表明，J积分的大小随防渗墙泊松比的增大呈线性减小。证明减小墙体的泊松比有利于提高防渗墙的抗水力劈裂能力。此外，与弹性模量对J积分的影响相类似，降低墙体的泊松比能够显著提高发生水力劈裂的最低水位要求。

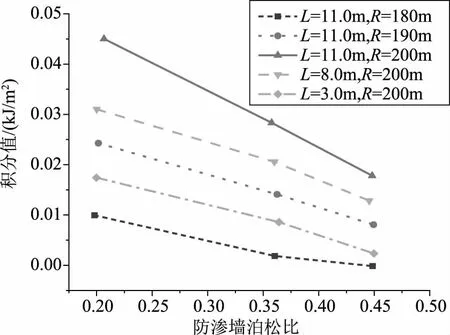
图6 防渗墙泊松比对水力劈裂的影响

图7得到了防渗墙密度对水力劈裂的影响。结果表明，J积分的大小随防渗墙密度的增大呈线性减小。但当裂缝长度为11m时，墙体的密度对J积分的大小影响不显著。相同库水位下。裂缝长度越大，J积分的值越大。综合来看，与弹性模量对J积分的影响相类似，提高墙体的密度能够显著提高发生防渗墙的抗水力劈裂能力。

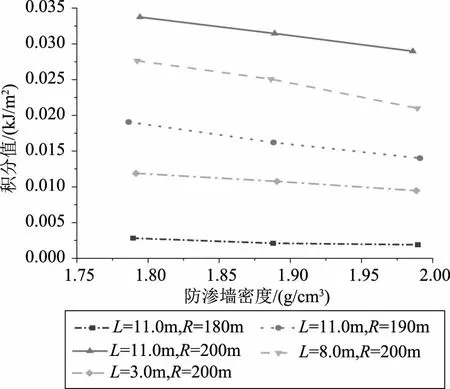
图7 防渗墙密度量对水力劈裂的影响

4 结语

本文依托某土石坝水利工程，采用ABAQUS分析了土石坝防渗墙的物理参数对水力劈裂效应的影响。结果表明J积分值随水位增大而增大。相同水位工况下，J积分数值的大小，随裂缝长度的增大而增大；相同库水位下，J积分值的大小随裂缝长度的增大而增大；J积分的大小随防渗墙弹性模量的增大呈非线性增大，随防渗墙泊松比的增大线性减小，随防渗墙密度增大而线性减小。提高防渗墙的弹性模量、降低墙体的泊松比及增大墙体的密度可显著提高防渗墙的抗水力劈裂能力。由于数值模拟结果与实际大坝的运行条件有较大差异，研究结果需要在工程实践中进一步的研究。