基于扩展傅里叶函数的VIC模型参数敏感度分析

白天竺

(辽宁省铁岭水文局，辽宁 铁岭 112000)

分布式水文模型可综合考虑流域下垫面条件变化对水文模拟的影响，近些年来在国内分布式水文模拟得到广泛应用[1]。分布式水文模型将流域离散成不同计算单元，通过设置各计算单元的模型参数，来实现流域分布式产汇流计算[2]。多个研究成果表明[3-8]，分布式水文模型由于各计算单元参数较多，其参数率定较为复杂，需要通过对分布式水文模型参数进行敏感性分析后，对敏感度较高的参数进行率定，从而提高模型参数率定的效率[9]。当前，在分布式水文模型参数敏感性分析较为成熟的方法为傅里叶函数[10-15]，其通过对模型进行敏感指数的分析，从而对各模型参数敏感度进行排序，但传统傅里叶函数由于不能考虑各参数之间的关联度，使得其在分布式水文模型参数敏感度分析时，对各参数进行单一敏感度的分析，敏感度分析在不同区域容易出现不同分析结果。为提高分布式水文迷行参数敏感度分析的效率，采用扩展傅里叶函数，综合考虑分布式水文模型参数之间关联程度，并以VIC模型为具体实例，探讨扩展傅里叶函数对VIC模型参数敏感度分析的适用性。研究成果对于分布式水文模型参数敏感性分析具有参考价值。

1 研究方法

扩展傅里叶函数可通过降低参数分析样本数据系列来提高模型参数敏感性分析的效率。模型参数的敏感性通过设定不同参数之间的敏感幅度来进行设定，模型参数敏感度随着其敏感幅度的增加而增加，扩展傅里叶函数对分布式水文模型参数进行标准化处理：

x=(x1，x2，…，xn)

(1)

其中在标准化处理的基础上对其进行均化处理：

(2)

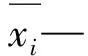
采用有效采样方法对模型参数敏感性分析进行数据处理，从而提高模型参数的可识别性，在进行参数处理时主要采用映射函数来建立不同参数之间的关联度：

xi=Gi[sin(Wis+φi)]

(3)

式中，s—参数之间的关联因子；Wi—参数敏感度变幅区间，通过设置不同变幅区间来对参数敏感度进行调整；Gi—参数搜索因子；φi—模型参数组合随机值。

各参数之间的映射函数采用Saltelli函数进行计算：

(4)

式中变量含义同前文所述。

在参数变幅区间内对样本序列进行选取，模型所用参数敏感度当参数关联因子S发生变化时呈现曲线变化，其变幅区间设置方程为：

Wi=MOD[i，int(wmax/2M)]

(5)

式中，MOD—函数取余数的计算符号；M—模型变量因子；Nr—模型分析变量个数。

分布式水文模型参数敏感度评价时主要基于映射函数的确定，其模型参数敏感度评价指标计算方程分别为：

(6)

(7)

(8)

式中，C—关联系数；R—洪峰相对误差，%；A—洪水过程确定性系数指标；Q—流量实测值，m3/s；Q′—计算的流量值，m3/s；N—计算序列个数；n—场次洪水数目。

模型参数敏感度在评价基础上采用各变量相互方差值进行计算：

(9)

对其进行转换计算：

Si=Di/D

(10)

Si，j=Di，j/D

(11)

式中，D—参数敏感度方差总值；Si—模型不同计算单元的参数敏感度方差值；Si，j—不同计算单元不同计算变量的参数敏感度方差值。

扩展傅里叶函数对分布式水文模型参数的敏感度进行求和计算：

(12)

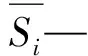
2 分布式水文模型参数敏感度

2.1 敏感度计算

以铁岭地区开原水文站以上流域作为研究区域，结合开原水文站1990—2020年实测洪水数据，分别采用扩展傅里叶和传统傅里叶函数对分布式水文模型VIC模型主要参数进行敏感度分析，分析结果见表1，并对VIC模型主要参数组合进行敏感度幅度分析，结果如图1所示。

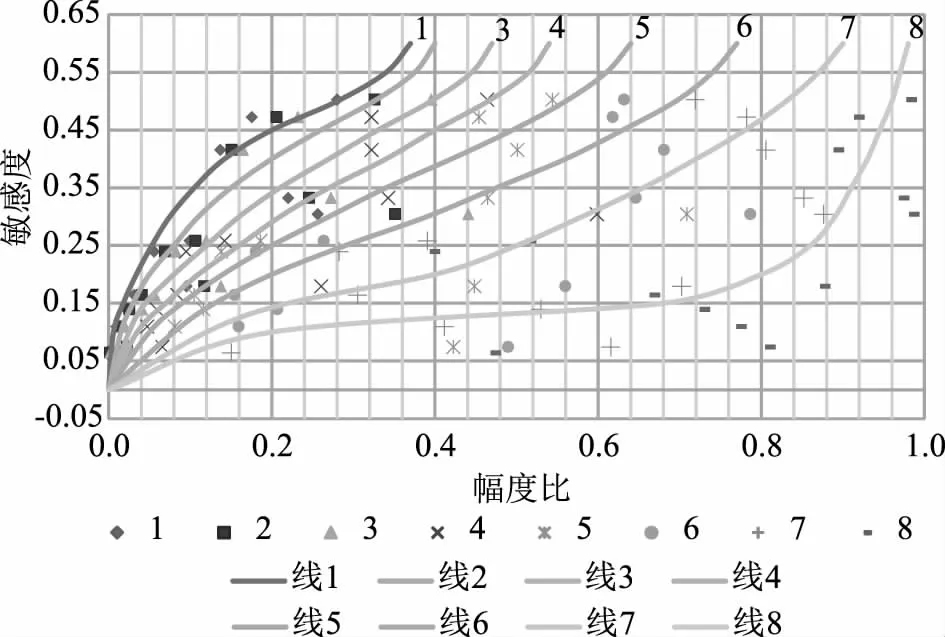
图1 扩展傅里叶函数不同模型参数组合的敏感幅度分析结果

从分布式水文模型VIC模型参数敏感度计算结果可看出，流域最大流速参数对于中小型河流洪水过程影响较大，而对于大型河流其洪水模拟影响相对较小，因此其敏感度较低。而采用传统傅里叶函数计算的VIC模型参数敏感度低于0.15的分别为洪水过程基流处理的非线性因子和土壤含水层第二层厚度，通过分析以上2个参数对于流域洪水模拟影响较高，传统傅里叶函数敏感度分析合理性程度不高，而扩展傅里叶函数下以上2个参数的敏感度均高于0.15。通过对VIC模型主要参数的敏感度进行分析，扩展傅里叶函数下下渗指数曲线的敏感度最高达到0.5795，敏感度最低的为流域最大流速，而传统傅里叶函数下敏感度最高的也为下渗指数曲线，其敏感度为0.5510，参数敏感度最低的为土壤含水层第二层厚度，2种方法下的参数敏感度不具有一致性，这主要是因为扩展傅里叶函数可综合考虑不同模型参数之间的关联度，因此其对模型参数敏感度分析要总体要比传统傅里叶函数要更为合理。从扩展傅里叶函数下不同模型参数组合下的敏感幅度分析结果可看出，在相同幅度比下模型下渗曲线指数变化幅度较大其敏感度也越高。

2.2 洪水模拟影响评价

分别结合扩展傅里叶函数和传统傅里叶函数下对参数敏感度分析结果，对比分析其对洪水模拟影响程度，结合铁岭地区开原水文站2010—2017年场次洪水资料，将不同方法参数敏感度较高的VIC模型的8个参数作为模型参数率定值输入，分别对比不同参数敏感度分析方法对洪水模拟的影响。对比结果见表2。

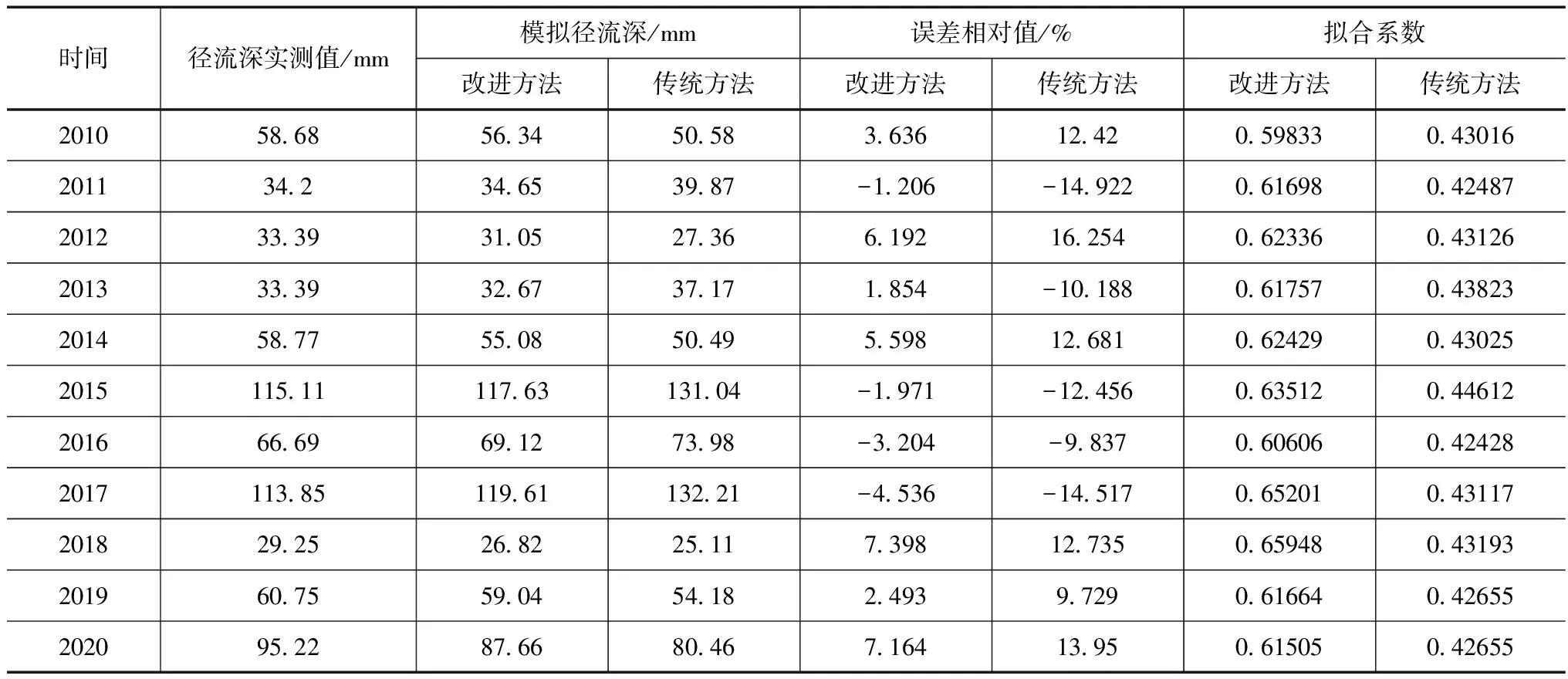
表2 洪水模拟影响程度评价结果

从扩展傅里叶函数和传统傅里叶函数参数敏感度分析结果对VIC模型洪水模拟影响分析结果可看出，采用扩展傅里叶函数对分布式水文模型VIC模型参数进行敏感性分析后，针对敏感度高于0.15的参数进行率定，而对于敏感度低于0.15的参数不进行率定，可明显提高分布式水文模型VIC模型在大型河流计算单元较多情况下的参数率定效率，可一定程度提高模型洪水模拟的精度，相比于传统傅里叶函数，其明显改善了开原站分布式水文模拟的精度，采用扩张傅里叶函数下其各场次洪水模拟相对误差均在±10%以内，相比于传统傅里叶函数，其洪水模拟相对误差均值可降低8.59%。此外，其对各场次洪水过程确定性系数也有所改善，分布式水文模型由于考虑流域下垫面条件，其对流域出口洪水模拟的确定性系数总体较低，而采用扩展傅里叶函数后相同降水条件下其洪水模拟的确定性系数均可在0.5以上，相比于传统傅里叶函数有所改善。

3 结论

(1)采用扩展傅里叶函数进行分布式水文模型参数敏感度分析时，对于参数敏感度高于0.15的参数进行率定，而对于敏感度低于0.15的参数可不进行率定，可提高分布式水文模型不同离散单元参数率定的效率。

(2)采用扩展傅里叶函数进行分布式水文模型参数敏感度分析时，各参数之间的映射函数应选用Saltelli函数，从而使得参数关联因子S呈现曲线变化。

(3)扩展傅里叶函数对于中小型河流分布式水文模型参数敏感性分析的适用性还需要进一步探讨。