坝口河沥青混凝土心墙风化料坝应力变形特性研究

罗 林，颜 明，李金成

(昭通市水利水电勘测设计研究院，云南 昭通 657000)

在过去的50年中欧洲和日本已经广泛地采用沥青混凝土作为土石坝的防渗材料[1]，最早的沥青混凝土心墙坝是葡萄牙1949年建成的Vale de Caio坝，高45m。作为坝体的防渗材料，沥青混凝土心墙主要具有以下优点[1]：良好的柔性、变形能力、抗震性、耐久性、防渗性和自愈性等优点。20世纪中期以来 欧洲、北美、中国和日本等地修建了大量的沥青混凝土心墙坝[2-3]。

受沥青混凝土心墙厚度较薄、受力后水平变位较大以及“拱效应”等因素影响，作为大坝的唯一防渗屏障，心墙的安全性问题、应力变形特性和水力劈裂越来越受到国内外研究人员的关注[4-5]。

本文基于邓肯-张非线性弹性模型，对坝口河水库沥青混凝土心墙坝的施工过程和蓄水期开展三维有限元应力变形分析，分析中考虑了上游坝体蓄水后的湿化变形，并对沥青混凝土心墙是否发生水力劈裂进行判别。本文工作为工程设计提供科学依据，对科学、合理地安排施工、制定蓄水方案具有指导意义，同时也可作为同类沥青混凝土心墙坝工程提供参考。

1 工程概况

坝口河水库位于云南省昭通市镇雄县东南部镇雄小河上游一级支流一头河干沟河段，距镇雄县城约9km，属乌江水系。水库坝址地理坐标：东经104°55′29″，北纬27°26′34″。该水库坝址区有乡村公路通过，交通较为便利。

大坝最大坝高71.40m，坝顶高程1609.20m，防浪墙顶高程1610.40m，坝顶宽度为10.0m，长度158m。坝体上游坝坡自上而下分别为1∶1.9、1∶2.0、1∶2.2，设有2级马道，宽2.0m，马道高程分别为1589.20、1569.20m；下游坝坡自上而下分别为1∶1.9、1∶2.0、1∶1.8，坝下游设有2级马道，宽2.0m，马道高程分别为1589.20、1569.20m；排水棱体顶高程1569.20m。坝体分区由上游至下游依次为上游填筑区(强-弱风化料)、过渡层、沥青混凝土心墙、过渡层、下游填筑区(强-弱风化料，弱风化料)、排水棱体组成。

沥青混凝土心墙防渗体顶部高程1608.90m，心墙顶部厚度0.5m，高程1594.20～1574.20m厚0.7m，高程1574.20～1554.20m厚0.9m，高程1554.20m以下厚1.1m。心墙底部设C25混凝土基座。

坝口河水库大坝的平面图和剖面如图1—2所示[6]。

2 三维有限元计算

2.1 本构模型

邓肯-张模型能较好的反应岩土材料应力变形的非线性特征，参数意义明确，通过三轴试验即可获得模型全部参数，在土石坝分析中得到广泛的应用，积累了丰富的工程实践经验。沥青混凝土是一种胶凝体散粒材料，其矿物颗粒的自身强度远大于沥青的粘结强度，破坏形式也更接近于剪切破坏，因此采用邓肯-张模型模拟非线性应力变形特征也是合适的。因此本文有限元分析中采用邓肯-张模型来描述坝体的本构关系。

邓肯-张E-B模型[7-8]的主要计算公式如下：

式中，Et—切线变形模量，kPa；K—切线模量基数；n—切线模量指数；φ—材料的内摩擦角，(°)；c—材料凝聚力，kPa；Rf—破坏比；Eur—卸载及再加载的弹性模量，kPa；Kur、nur—由试验确定的两个系数，其确定方法与K、n相似；Bt—体积模量，kPa；Kb—体积模量系数；m—体积模量指数；pa—大气压，kPa，量纲与σ3相同。

水库蓄水后，坝体除了自重外还受到水压力、浮托力和湿化三方面的影响，其中湿化变形会引起散粒体材料的收缩，影响坝体的应力变形结果。本文计算采用沈珠江院士的Cw-Dw模型[9]考虑坝体湿化变形的影响。为合理地模拟沥青心墙实际受力状态，沥青心墙与过渡料之间设置Goodman接触单元[10]模拟接触特性。

2.2 计算模型及参数

根据工程的试验参数报告[11]，坝口河水库大坝的应力变形参数取值见表1。

采用河海大学工程力学研究所开发的水工分析系统Autobank建立坝口河水库大坝的模型，并对其有限元离散，有限元计算模型如图3。模型中x、y、z三个方向分别为坝轴向指向左岸，竖直向上，垂直坝轴向指向上游。

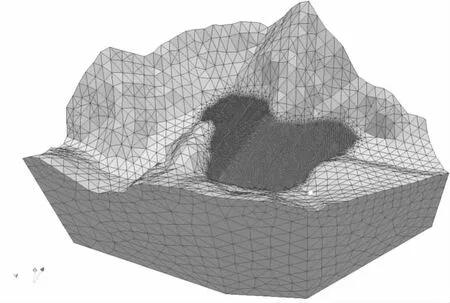
图3 大坝计算三维有限元模型

2.3 加载步及计算工况

在计算中按照大坝实际的填筑及蓄水过程进行模拟，采用分级加载的方式进行非线性模拟。共分12个加载步，其中1～8为大坝填筑至设计标高，9～12为蓄水加载步。为分析方便及简洁，本文主要列出完建期及蓄水后(正常蓄水位)两步结果并进行分析，竣工期考虑仅考虑地下水位和坝体自重影响。蓄水期分期蓄水加载至正常蓄水位，下游无水，荷载考虑为坝体自重、渗透力及坝体材料的湿化变形。

3 计算结果及分析

3.1 完建期计算结果

3.1.1位移结果

分层填筑坝体产生的沉降与一次加载填筑是有区别的，一次加载坝体内任意一点的沉降为该点以下土层沉降之和，假设土体为弹性均质体，则该沉降与该点至模型底部的平方成正比；若考虑分层加载，当填筑至某标高时，该点以下的沉降已经完成，即该点沉降为零，继续筑坝才能使该点产生沉降，由此计算得到的分层加载沉降体现为沿着坝高先增大后减小，顶部位移为0，最大位移发生在坝体内部。本次计算，完建期沉降最大值为25.15cm图4(b)，出现在1/2坝高偏上处，总量约为坝高的0.35%，其分布也符合一般分层加载筑坝的规律[12-13]，计算结果正常。

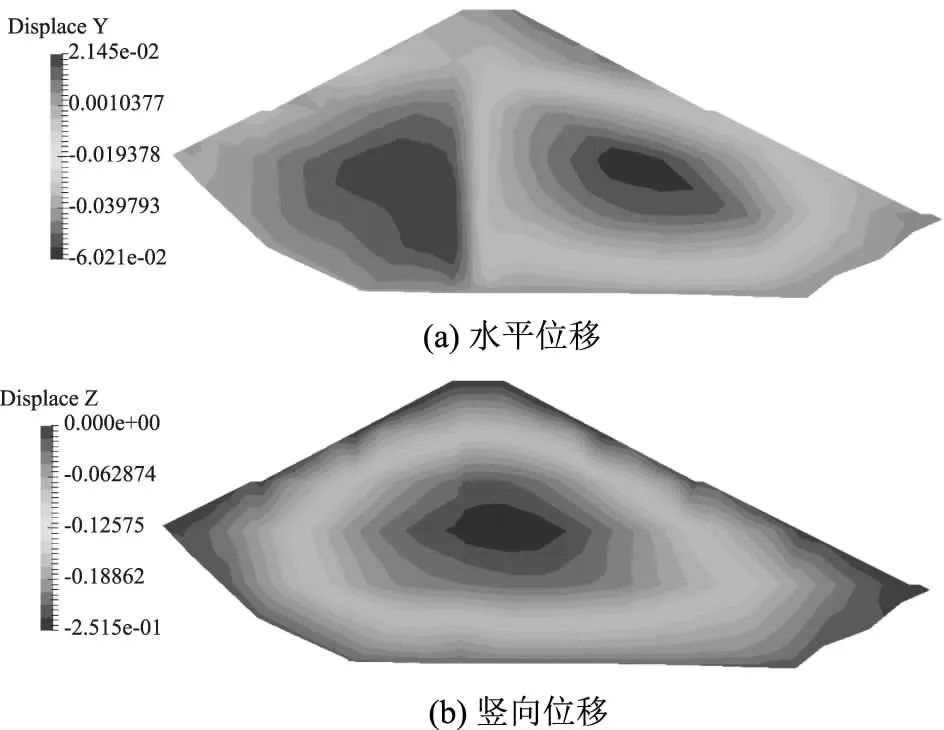
图4 完建期坝体位移云图

完建期坝体水平位移图4(a)主要为上、下游方向。受坝体体型影响，坝体上游部分的水平位移呈现向上游变位，最大值为2.15cm，发生在约2/5坝高附近，坝体下游部分呈现向下游变位，最大值为6.02cm，发生在约1/2坝高处。

3.1.2应力结果

图5(a)显示坝体断面最大压应力1775kPa，出现在坝体的底部位置的过渡层内，该区域填筑高度大且过渡层刚度较心墙大，受其影响压应力较大。

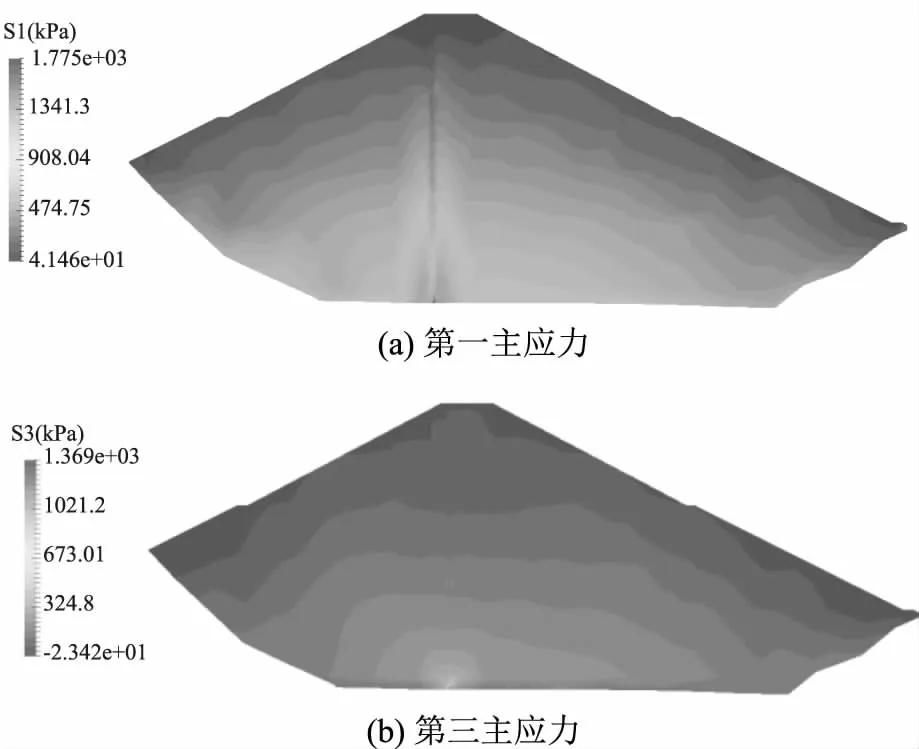
图5 完建期坝体主应力云图

坝体竣工后，随着坝体的沉降，坝坡上下游表面容易出现微小拉应力，最大值约-23.42kPa，深度较浅，不影响坝体的整体应力状态。完建期坝体应力水平最大约为0.601，应力状态良好。

整体而言，竣工期坝体基本处于三向受压状态。

3.2 蓄水期计算结果

3.2.1渗流结果

蓄水期渗流是影响坝体应力变形的重要因素，本处先对坝体进行蓄水期的三维渗流分析。水头与水压结果(图6(a)和图6(b))显示上下游堆石体内浸润面几近水平，其消耗水头差较小，绝大部分水头消耗发生在沥青心墙内，渗流状态良好，符合沥青心墙坝渗流状态的特点。

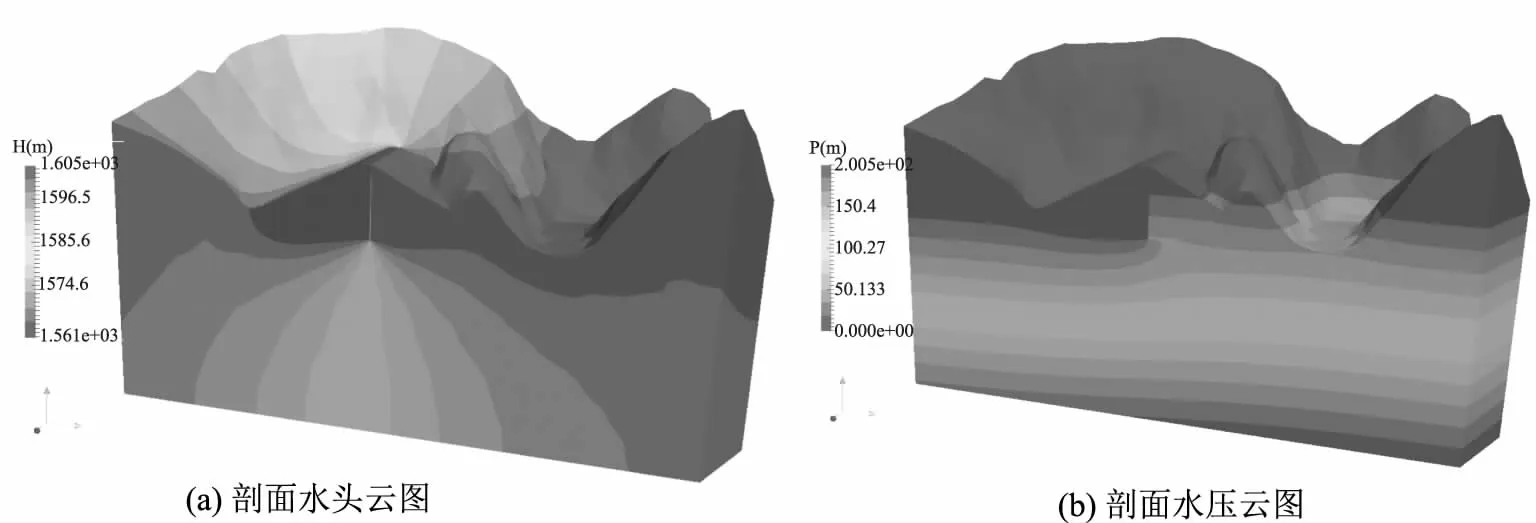
图6 正常蓄水位的渗流结果

3.2.2位移结果

蓄水期的坝体变形图如图7(a)，在渗流荷载作用下，坝体出现往下游方向的变形，坝体中部位移较两侧大，蓄水期心墙的y方向位移增量图(图7b)显示y方向位移增量主要出现在心墙中下部，最大为8.43cm，该区域为渗流荷载和坝体Y方向刚度两者综合出现的最大变位。坝体沉降大值为19.12cm，出现在大约1/2坝高处，沉降增量图(图7(f))显示在渗流荷载下，坝体上游表面呈现沉降，最大值为2.91cm，上游底部因为浮托力有向上的变位，最大值为3.19cm。

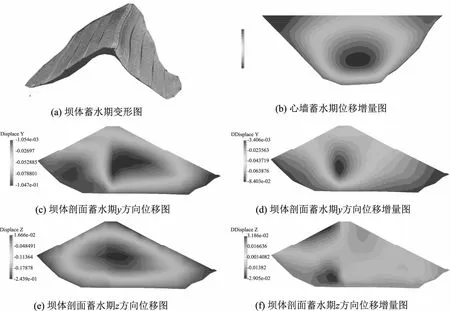
图7 蓄水期位移结果

蓄水期水平位移呈现整体往下游趋势，最大值为10.47cm，出现在心墙附近，水平位移增量图(图7(d))显示心墙坝在渗流荷载作用下心墙及过渡层位移较大，上下游坝壳出现往下游的挤压状变形。此时由于沥青心墙和坝体变形模量的差异，心墙附近出现明显的位移差。

3.2.3应力结果

相比于完建期主压应力结果，蓄水后下游侧过渡层底部出现了较大的压应力(图8(a))，最大值约1992kPa，拉应力整体较小，不足10kPa，主要出现在坝面处。由于沥青心墙的变形模量较小，同时接触面单元的存在，心墙能较好的适应坝体的变形，未出现较大拉压应力。

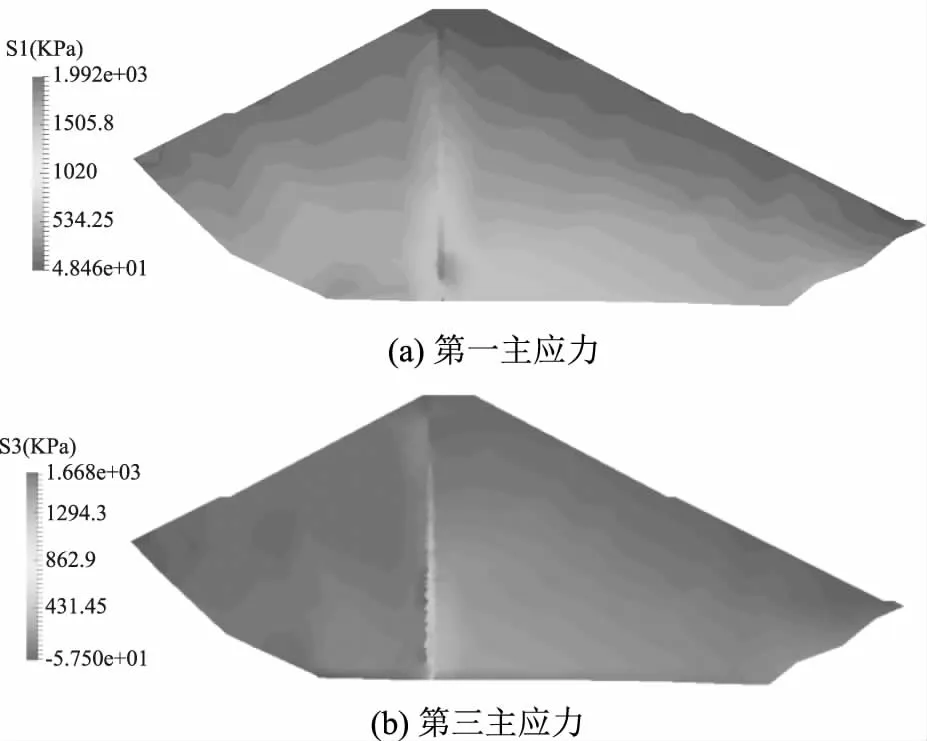
图8 蓄水期坝体主应力云图

蓄水期坝体应力水平最大约为0.805，整体而言，蓄水期坝体仍处于三向受压状态。

3.3 水力劈裂分析

当水压力超过防渗体中的压应力可能出现水力劈裂现象。坝体内的沥青混凝土心墙在受水压力作用下出现拱效应，如果拱效应过大将发生水力劈裂而导致心墙破坏，因此需要判别心墙是否发生水力劈裂[14]。文献[15]规定，应采用心墙上游面的竖向应力和水压力进行比较，其依据是拱效应会使防渗体的竖向应力减小。文献[16]建议用中主应力判别水力劈裂是否会发生，原因为中主应力比竖向应力小，使用中主应力更加偏于安全。竖向应力和中主应力的方向都与水压力垂直，竖向应力的方向沿竖直方向，中主应力的方向与坝轴线方向大体一致。水进入裂缝之后，作用方向分别与竖向应力和中主应力的方向相反，与二者进行抗衡。如果用竖向应力与水压力进行比较，实际上是判别水是否会沿着竖直方向将心墙劈开水平裂缝；如果用中主应力与水压力进行比较，则是判别水是否会沿着坝轴线方向将心墙劈开竖向裂缝。

为此，本文在心墙上游表面设置19个特征点(图9)，分别采用水压力与竖向应力的比值和水压力与第二应力的比值，对水力劈裂的安全性进行了判别，特征点分析结果见表2。可见采用两种方法进行水力劈裂判断，各水位工况下结果都是安全的，因此心墙发生水力劈裂的可能性很小。

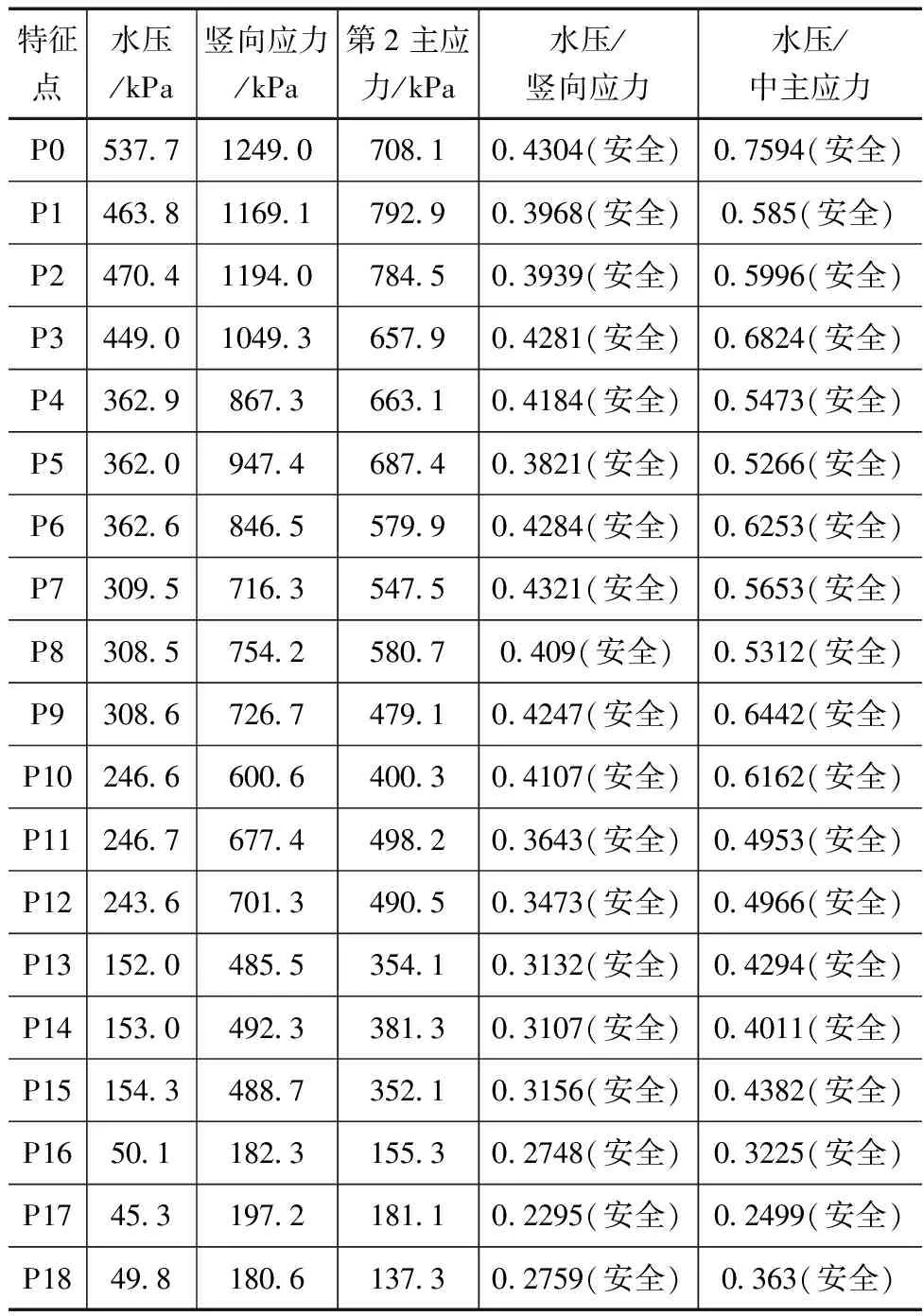
表2 特征点水力分析表

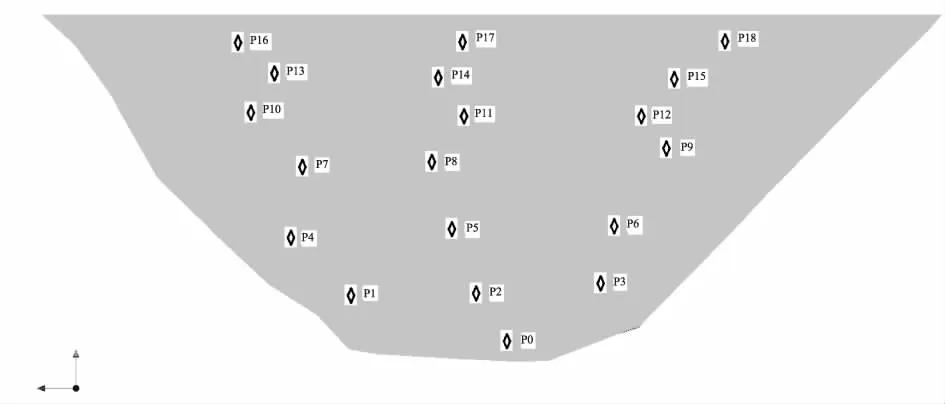
图9 水力劈裂特征点位置(心墙上游面)

4 结语

(1)坝体变形分布符合一般规律，完建期最大沉降25.15cm，约为坝高的0.35%，水平位移最大为6.02cm。蓄水后最大竖向位移为19.12cm，坝壳最大水平位移为10.47cm，心墙最大水平位移为8.43cm。

(2)坝体基本处于三向受压状态，沥青心墙具有良好的柔性，未出现较大的拉、压应力，坝体应力水平状态比较理想。

(3)两种判别方法结果表明发生水力劈裂的可能性很小。

(4)邓肯-张模型能较好的体现材料非线性，但更为科学的描述应力变形尚需要更加精细的本构模型。

本文结果表明，坝体和心墙的变形均处于合理范围，筑坝材料满足强度要求。可为同类工程设计管理提供参考。