基于结构动态可靠度的水闸使用寿命预测分析

阿里木·阿布都克然木

(塔里木河流域干流管理局，新疆 库尔勒 841000)

水闸作为一种低水头水工建筑物，具有挡水和泄水的双重功能，在水利工程建设中具有广泛的应用和重要的地位。我国的水闸大多建设于上世纪中期，受到当时经济技术水平等诸多因素的制约，普遍存在工艺落后、配套不足的问题，病险问题比较突出[1]。因此，随着我国科技和经济实力的提升，水闸的安全性问题日益受到重视，并着力进行除险加固，以提升水闸的运行安全。关于水闸的安全评价，目前国内外学者已经进行了广泛而深入的研究，但是仅通过现场监测和分析对水闸进行安全性评价是不够的，因为水闸的安全性是一个动态变化的过程，单纯的安全性评价并不能较好预测其结构安全的动态发展趋势[2]。因此，对水闸的剩余使用寿命进行合理预测，有助于对水闸结构及时进行维修、改造和加固，保证水闸处于良好的服役状态，有效减少安全事故的发生。同时，还可以为水闸管理部门提供维护管理的决策依据，实现服役周期内除险加固成本的有效控制。因此，以概率分析为基础的水闸结构寿命动态可靠度分析就成为当前研究的重要方向。

1 计算模型

1.1 计算原理

目前，国内外学者在时变可靠度方面进行了广泛而深入的研究，且颇有成效。Nowak在进行混凝土结构桥梁可靠度研究过程中充分考虑了抗力退化的影响，使评价结果更接近工程实际[3]；B.Radhika在研究中以既有结构的静态随机动力激励，提出一种专门针对结构系统时变可靠性的分析方法[4]。王光远提出动态可靠度的概念，并对混凝土结构的时变可靠度进行了深入分析和研究[5]。陈远通过构建完整的抗力随机过程模型，实现了利用可靠度理论对结构和体系时变可靠度的求解[6]。显然，上述所有研究均可以为此次研究的顺利进行提供理论层面的支持和借鉴。当然，对水闸而言，其闸室和地基为一个有机整体，在荷载作用下会有沿着地基面滑动的可能性，甚至荷载过大时还可能出现失稳破坏[7]。基于此，此次研究中引入各种失效模式，对闸室和地基之间的专递能力进行分析计算，验算其抗滑稳定性和可靠度，最后利用时变可靠度理论对水闸的使用寿命进行预测分析。

1.2 极限功能函数

在水闸工程的设计和校核计算中，结构稳定是最为重要的内容之一，需要根据工程不同结构的特点和功能需求，建立可靠度分析的极限功能状态函数[8]，具体的计算状态及表达式如下。

1.2.1闸室抗滑稳定极限状态

Z1=f∑G+CA-∑P=0

(1)

式中，∑G—所有竖向应力之和，kN；∑P—所有水平应力之和，kN；f—闸室混凝土和地基之间的摩擦系数；C—闸室底板和地基的粘聚力，kN；A—闸室底板总面积，m2。

1.2.2下游闸趾抗压强度极限状态

(2)

式中，f0—地基承载力，kPa；∑M—闸室上竖向和水平荷载对底面垂直水流方向的形心轴力矩，kN·m；W—闸室上竖向和水平荷载对底面垂直水流方向的形心轴截面矩。

1.2.3上游闸踵不出现拉应力极限状态

(3)

1.2.4上下游应力比控制极限状态

(4)

式中，k—应力允许比值。

按照《水闸设计规范》(SL 265—2016)中的相关规定，闸室基地应力的最大值和最小值的比值应该满足表1。

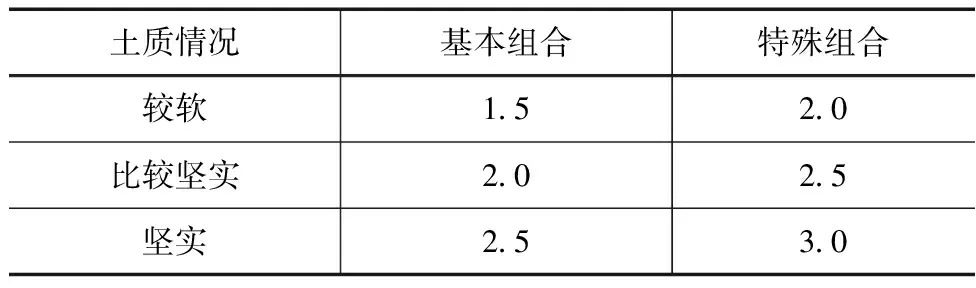
表1 闸室基底应力最大值和最小值比值允许值

1.3 寿命终止标准

水闸的使用寿命指的是在正常维护和使用的条件下，工程本身能够发挥功能的时间，也就是开始使用到达到破坏极限状态的时间[9]；剩余使用寿命指的是现状水闸在不采取修复加固措施，仍能够保持其基本功能而可以继续使用的年限。当然，这里的结构安全和功能发挥是概率层面的内涵，并不具有绝对性，因此使用寿命本身也是一个不可预测的随机变量[10]。

当然，水闸的失效概率大于设定值时，并不是工程已经倒塌需要拆除，而是某些功能已经不能正常发挥。按照该领域的研究成果和相关规范要求，包括水闸在内的结构构件承载极限状态目标可靠指标βt不应低于表2的规定。

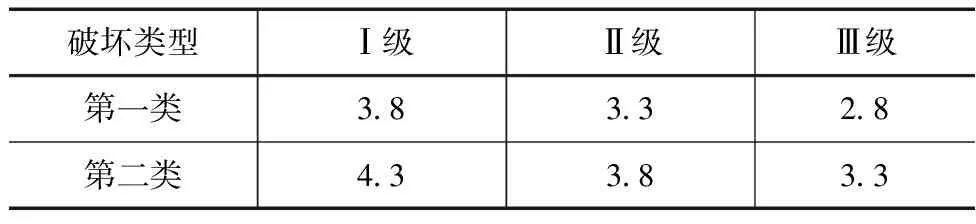
表2 水工结构构件目标可靠指标βt允许值

按照上述思路，水闸工程的剩余寿命计算流程如下：①以水闸的寿命终止指标为基础确定目标可靠度；②收集与水闸工程有关的物理特征、相关参数以及环境等方面的资料和数据；③构建水闸结构的荷载效应以及抗力衰减模型；④构建水闸结构极限状态方程和失效模式；⑤按照合理的时间步长对动态可靠度进行计算；⑥根据小于目标可靠度的动态可靠度对应时间确定水闸的剩余使用寿命。

2 工程应用

2.1 工程背景

某水闸于1967年1月动工，1970年6月竣工，为大(Ⅰ)型水利工程。经过约50a的运行，工程主要建筑物破损、老化严重，已危及工程的安全使用，拟采用水闸主体重建的加固处理方案。工程与2015年5月开始施工建设，2016年5月竣工验收并投入使用。竣工后的水闸主要水工建筑物为一级，按照100a一遇洪水标准设计，按照300a一遇洪水标准校核。水闸的单孔净宽为7.5m，两孔一联，共5联，在闸室段上设有检修工作桥、排架和启闭机房等附属设施

2.2 计算模型与参数

根据失效模型和极限状态方程，水闸的安全稳定状态的影响因素较多并具有随机性，而这些随机变量的统计资料往往比较缺乏。因此，研究中选择水闸的基底面与基土之间的内摩擦角、混凝土容重、上游水位、下游水位以及地基承载力作为研究中的参数随机变量，不考虑地震荷载、封冻期冰压力和泥沙压力的影响。结合工程设计运行资料和相关工程规范，确定上述参数的均值、变异系数和分布类型，结果见表3。

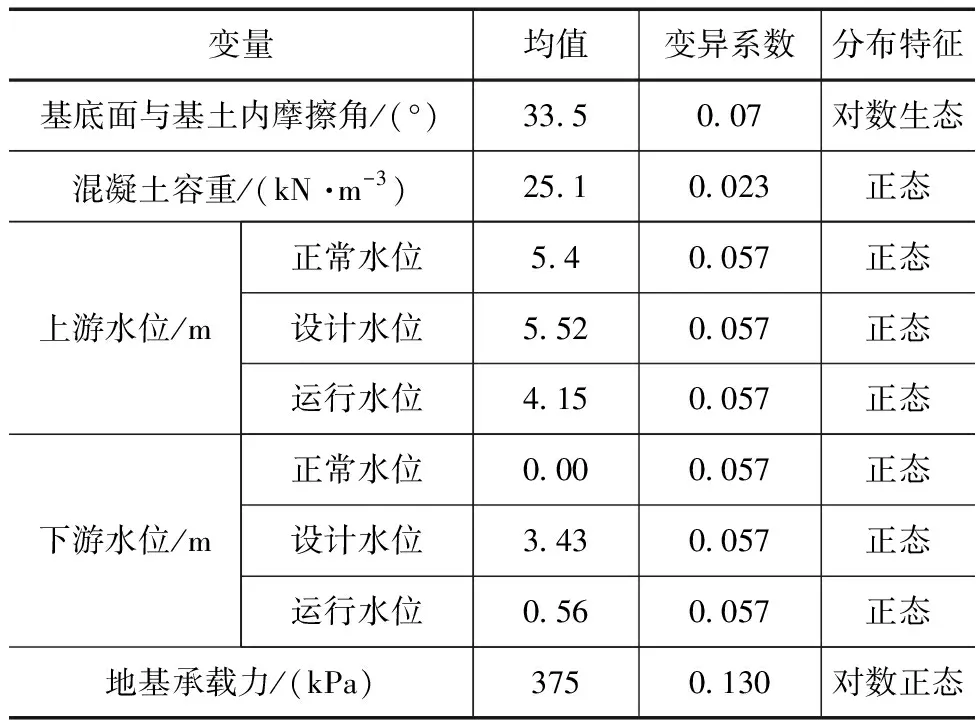
表3 模型随机变量特征统计表

在水闸的长期服役过程中，受到内部和外部诸多环境因素的影响，混凝土重度、摩擦系数以及粘聚力等参数均会随着时间的延长而不断减小，而地基土在长期荷载的作用下，会产生一定的压密效应，土性会有所提高，因此承载力的特征值和极限值也会相应增加。但是，由于工程建设中水闸的地基处理效果良好，因此在服役过程中的提升值较为有限。同时，工程项目区的地基土为低压缩土层，因此地基沉降量满足要求且该失效模式对水闸的后续失效不存在影响，因此不再对地基承载力的状态进行相关参数和时变可靠度的计算。基于此，研究中充分结合背景工程的资料和相关研究文献，确定主要随机变形的时效变化，分别计算背景工程在运行20～90a之后的具体值，结果见表4。

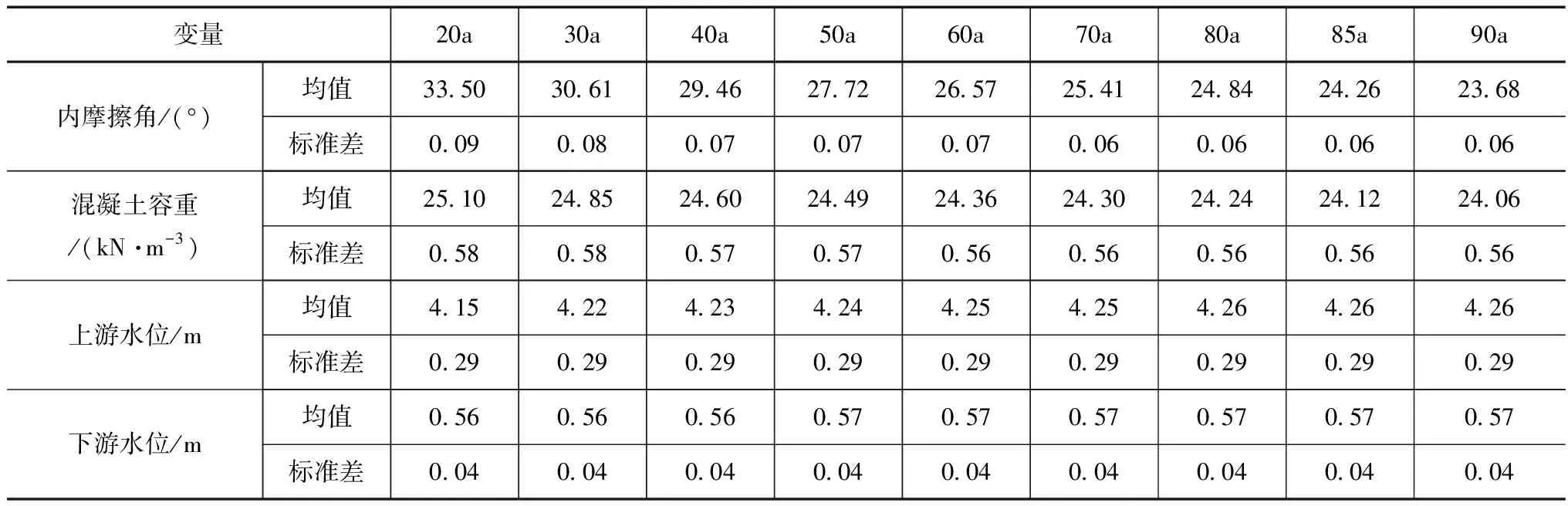
表4 各变量在使用期内的变化情况统计计算结果

2.3 计算结果与分析

水闸的服役寿命预测需要以水闸的安全现状为基础进行。基于此，为了保证除险加固设计的可靠性，首先对不同工况下的水闸静态可靠度进行计算分析。计算过程中首先将表3中的随机变量值代入计算模型的极限状态方程，并利用蒙特卡罗法计算出可靠度指标，结果见表5。

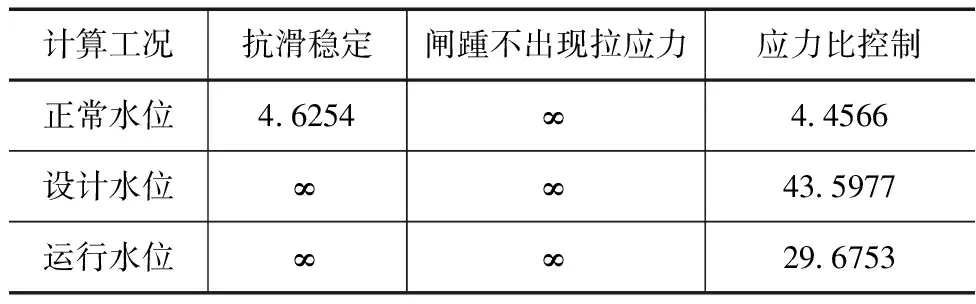
表5 水闸静态可靠度计算结果

由于背景工程的安全等级为一级，因此需要按照第一类破坏类型分析。从表中的计算结果可以看出，四种失效模式在3种不同运行工况下的可靠度指标均显著大于3.8，说明在进行除险加固之后水闸的安全系数显著提高，完全满足规范要求。

当然，随着水闸服役年限的增加，各变量参数也处于动态变化之中，因此研究中将表4中的随机变量值代入极限状态方程，对相应的可靠度进行计算。鉴于正常蓄水位工况为最危险工况，此时工作闸门关门挡水，水闸的上游有水，下游无水，上下游水位相差最大，因此水平压力也最大。所以，研究中仅针对该工况进行计算。计算过程中以除险加固工程完工投入运行为0a，具体的计算结果见表6。

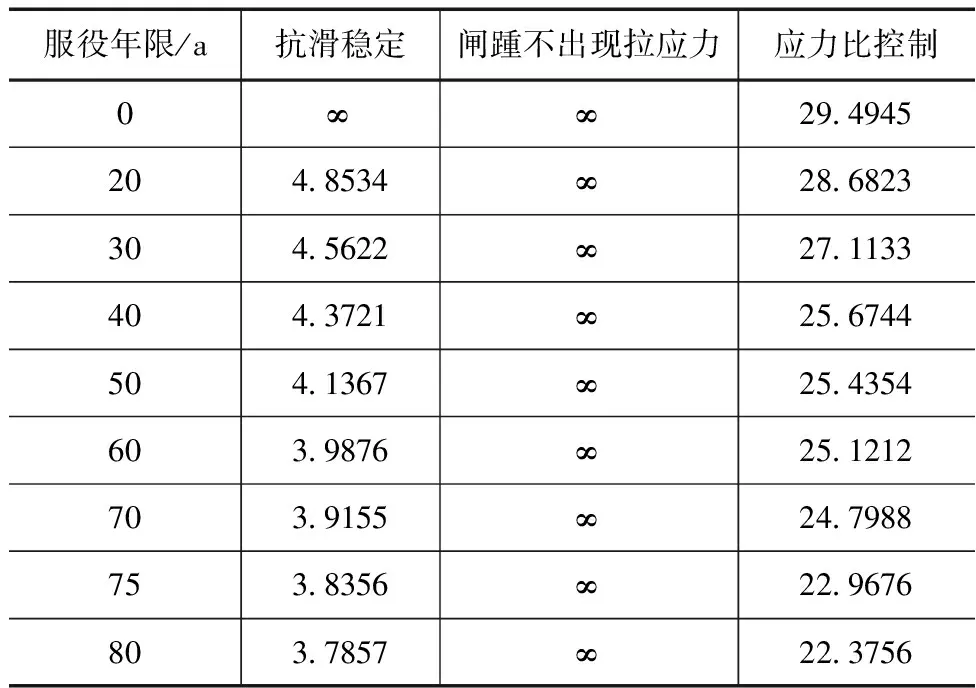
表6 水闸时变可靠度计算结果

根据背景工程除险加固设计，水闸的使用年限为90a。由于背景工程的安全等级为一级，因此需要按照第一类破坏类型分析，因此剩余使用寿命计算中的目标可靠度值为3.8。从计算结果来看，变化最快的是抗滑稳定失效模式。另一方面，在水闸的使用过程中，闸踵拉应力和应力比均满足要求，不会因为该指标不满足要求而失效。

在水工结构可靠度统一标准中指出，某一个结构件的失效并不意味着整个水利工程结构的失效，也就是单个结构的可靠度并不能代表整个结构体系的可靠度。但是，从本文的计算结果来看，由于闸踵出现拉应力导致破坏的可能性很小，而闸室滑动失效的概率显著偏大。另一方面，由于水闸工程的设计使用年限相对较长，必须要从偏安全的角度进行计算评价。基于此，此次研究中认为3种失效模式中由一个失效。由此可见，当加固完成后第75a时，抗滑稳定可靠度为3.8356，处于失效临界状态，达到剩余寿命的终止目标。当然，者并不意味着75a后水闸不能在使用，而是需要采取一定的补强加固措施，提高指标的可靠度。目前，水闸在加固后已经运行了7a，而计算中也没有考虑极端天气和自然灾害等因素的影响，因此实际寿命应该略小于75a。因此，建议水闸在继续60～65a时加强检测，必要时采取维修加固措施，以延长其继续使用时间。

3 结语

基于结构动态可靠度理论，对某加固后的水闸使用寿命进行预测，结果报名该水闸在加固后，可服役75a，75a后水闸的抗滑稳定可靠度将处于失效临界状态，若考虑极端天气和自然灾害情况，水闸的实际寿命会小于75a，建议在60～65a时加强水闸检测，必要时采取加固措施，以防止安全事故发生。由于受到研究对象复杂性和背景工程地理位置等因素的影响，没有考虑作用在闸室上的地震、台风等动力荷载，建立的寿命预测模型也相对比较简单，在今后的研究中需要关注和引入更多的服役寿命影响因素，实现对模型的不断改进和优化，使计算结果更贴近工程实际。