一类具有预设跟踪性能的约束控制器设计
刘勇华,潘则丞,乔瑜姣
(广东工业大学自动化学院,广东 广州 510006)
0 引 言
在工业生产过程中,出于安全与性能方面的考虑,通常要求控制系统满足各种约束条件,包括执行机构中存在的物理安全约束以及工业生产中的工艺性、经济性和社会性等指标约束.在系统运行过程中,若这些约束条件无法得到满足,工业生产将会受到很大的影响[1,2]。因此,建立约束控制理论来解决约束系统的控制问题具有重要的理论意义与实际价值[3-10]。经过十多年来学术界与工业界的努力,约束控制理论取得了很大的进展,涌现出Reference Governor[11]、模型预测控制[12]、滑模控制[13]、基于不变集的控制器设计[14]与极值搜索控制[15]等多种约束控制方法。
近年来,基于障碍Lyapunov函数(Barrier Lyapunov Function,BLF)的约束控制方法受到越来越多学者的关注[16-18]。针对一类含有输出约束的严格反馈非线性系统,文献[16]分别提出了基于对称BLF和非对称BLF的状态反馈控制算法,所设计的控制器不仅能够满足给定的输出约束条件,且能实现渐近跟踪。在文献[16]的基础上,文献[17]通过构造非对称时变BLF解决了一类含有时变输出约束的严格反馈非线性系统的控制问题。针对一类具有全状态约束的严格反馈非线性系统,文献[18]给出了一种基于积分型BLF的自适应神经网络控制方案。该方案在满足系统状态约束的同时,可保证闭环系统所有信号是半全局一致有界的。
值得指出的是,上述基于BLF的约束控制方法均无法直接对系统的输出或状态进行约束,仅能通过约束状态误差来间接约束系统的输出或状态,使得受约束输出或状态的初始值必须限制在一个比给定约束条件更小的区域内,因而所提控制算法具有较大的保守性。为解决这一问题,文献[19]采用非线性映射技术,将含有输出约束的非线性系统转化为无约束系统,设计了一种满足输出约束的自适应反推控制算法。文献[20]结合坐标变换与动态面控制方法,探讨了一类全状态约束非线性系统的自适应控制问题。然而,这些结果仅能满足系统的输出或状态约束,无法兼顾系统的瞬态与稳态性能。
为预先设定系统的瞬态与稳态性能,Ilchmann等受到高增益控制思想的启发,提出了一种漏斗控制(Funnel Control,FC)方法[21]。随后,文献[22]将该方法推广至一类Brunovsky型非线性系统。文献[23]进一步研究了一类具有未知幂次的高阶不确定非线性系统的预设性能控制问题,得到了一种基于BLF的漏斗控制方案。与此同时,Bechlioulis和Rovithakis利用误差变换技术,提出了一种预设性能控制(Prescribed Performance Control,PPC)策略[24,25]。在未知动态环境下,文献[26]和[27-28]分别探讨了具有未知控制方向的严格反馈非线性系统的预设性能镇定与跟踪问题。为同时满足系统的输出约束与预设性能约束,文献[29]通过选取合适的性能函数,设计了一种基于BLF的自适应控制算法。针对一类全状态约束的欧拉-拉格朗日系统,文献[30]利用BLF给出了一种预设性能自适应控制方案。然而,文献[29-30]中的控制方法不可避免地保留了BLF引起的保守性问题。此外,这些方法中的性能函数无法完全根据预先设定的瞬态与稳态性能进行选取,需要折衷考虑系统的输出或状态约束。
基于以上讨论,本文针对一类含有输出约束的严格反馈非线性系统,提出了一种具有预设跟踪性能的约束控制方法。该方法根据系统的输出约束和预设性能要求,设计了一种新颖的坐标变换。与基于BLF的控制算法相较,本文所提控制器的显著优点包括:1)采用坐标变换直接对系统的输出与跟踪误差进行约束,去除了BLF引起的保守性问题;2)性能函数不依赖于系统的输出约束条件,其选取具有更大的灵活性。最后,仿真结果表明了本文所提控制算法的有效性。
1 问题描述
考虑如下一类严格反馈非线性系统[18]
(1)
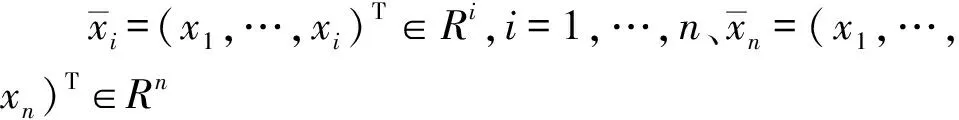
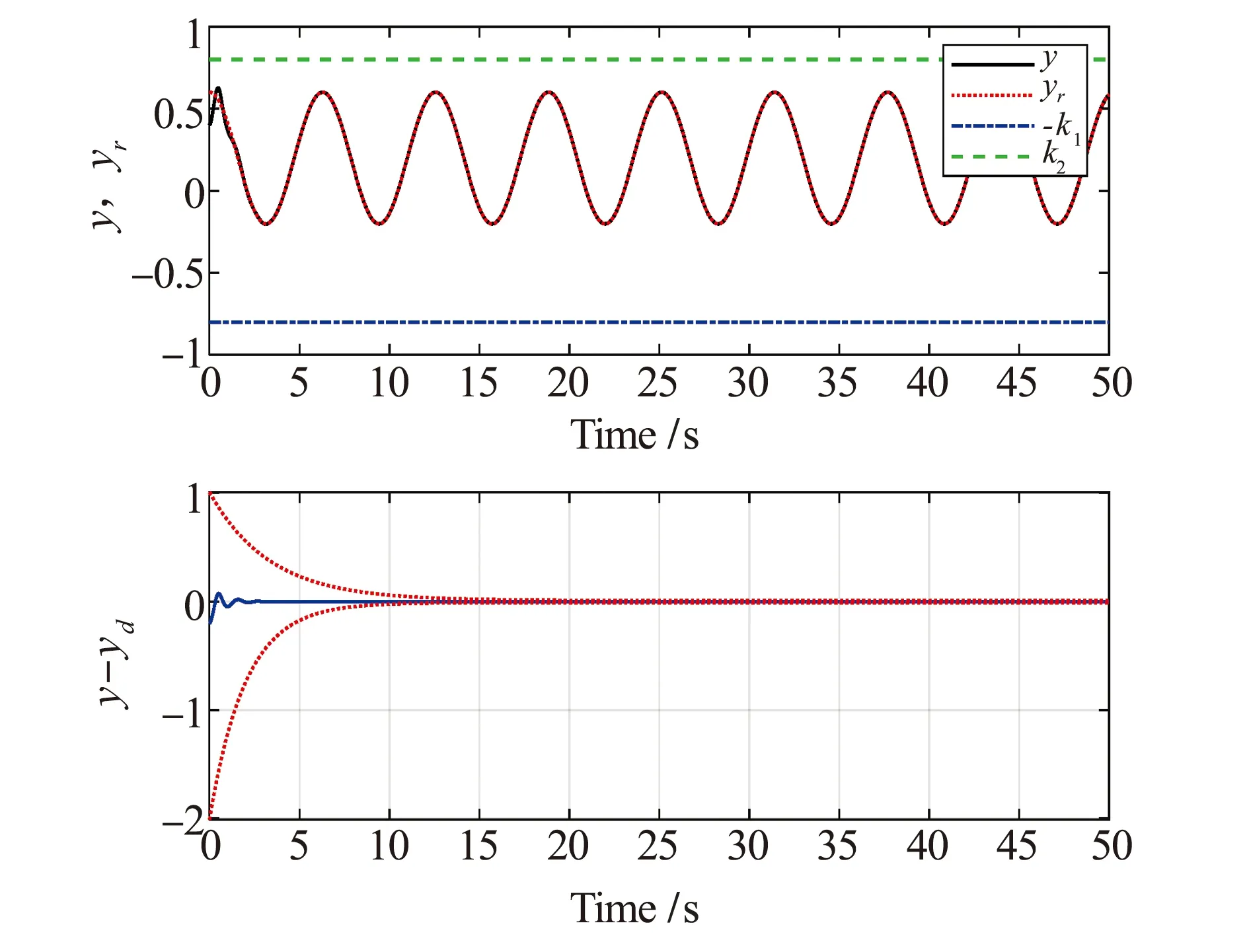
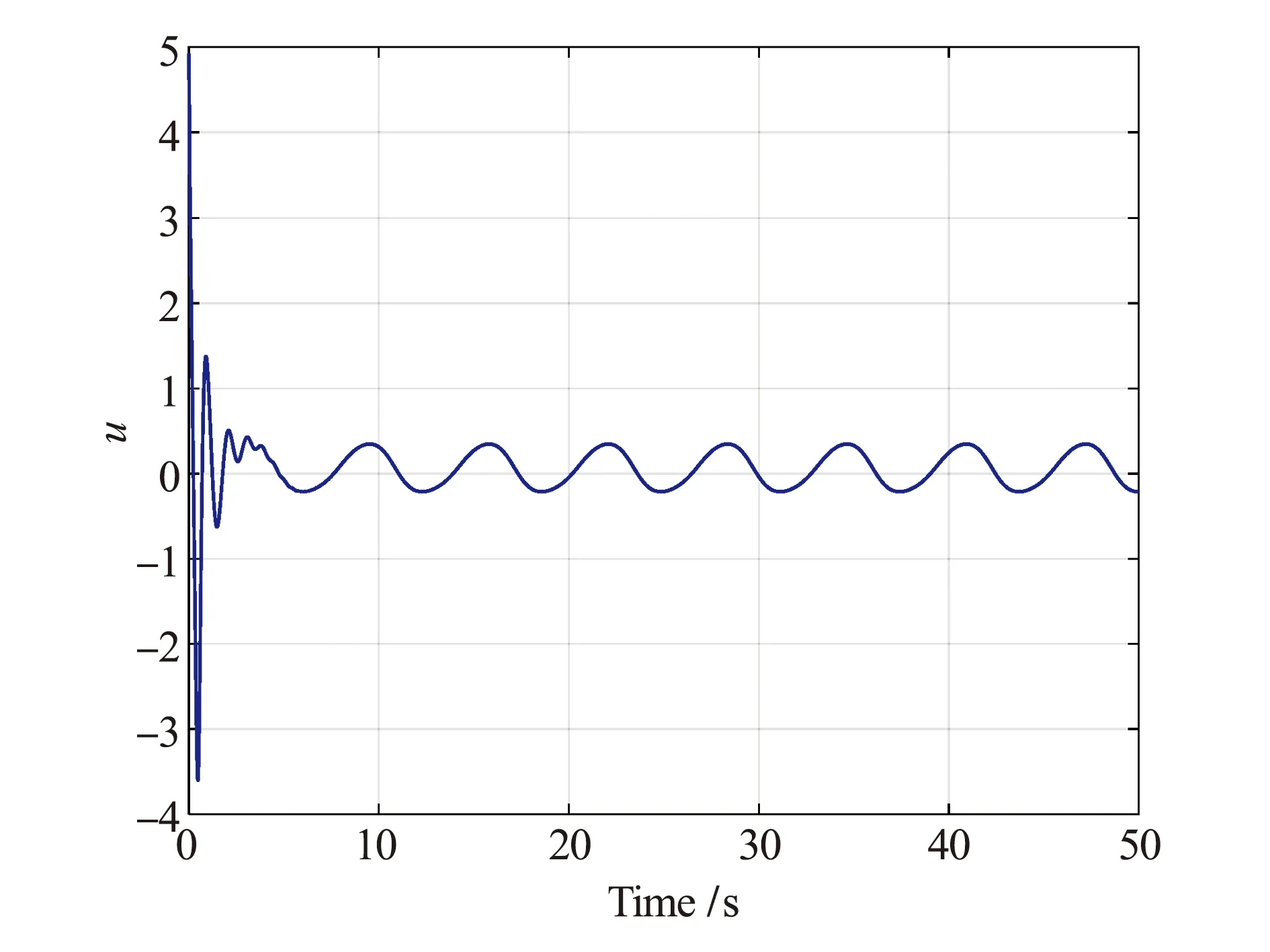
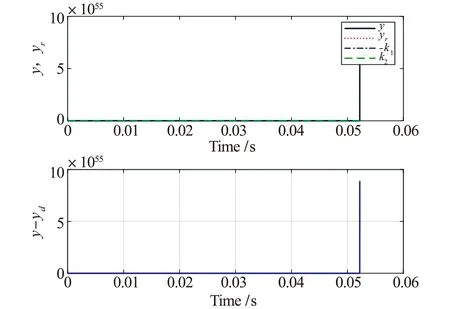
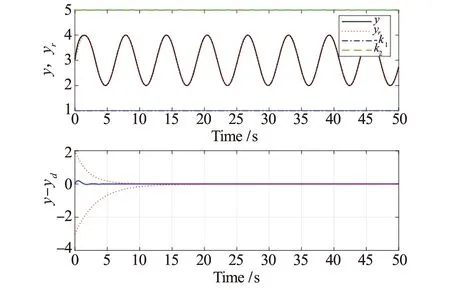
k1 (2) 公式中:k1,k2为约束常数,且k2>k1。 本文的控制目标:设计一个状态反馈控制器u,使得系统输出满足给定的约束条件(2),且跟踪误差y-yr保持在预设性能边界内,即 -ρ1 (3) 公式中:ρi(t),i=1,2为性能函数,满足 1)ρi(t)是正的且严格递堿; 2)limt→∞ρi(t)>0。 注1本文中性能函数ρi(t),i=1,2可选取为如下形式[22-23] ρi(t)=(ρi,0-ρi,∞)e-λit+ρi,∞,i=1,2 (4) 公式中:ρi(0)=ρi,0为预设性能函数的初始值;limt→∞ρi(t)=ρi,∞为稳态误差边界;ρi,0>ρi,∞>0、λi>0分别为误差收敛速度;ρi(0)需满足-ρ1(0) 引理1(LaSalle-Yoshizawa定理)[31]:针对非自治系统x=f(x,t),x(0)=x0,其中,f(x,t):Rn×R+→Rn满足局部Lipschitz条件。若存在一个连续可微Lyapunov函数V:Rn×R+→R满足 (ⅰ)V(x,t)>0和V(0)=0; (ⅲ)V(x,t)→∞当‖x‖→∞(径向无界), 公式中:W(x)为一个连续函数。则系统的所有解x(t)都是一致全局有界的,并且limt→∞W(x(t))=0。另外,当xe=0为系统的平衡点且W(x)>0时,系统在该平衡点为一致的全局渐近稳定。 为保证系统输出在给定的约束区间内,且跟踪误差z1满足预设的瞬态和稳态性能要求,定义如下坐标变换 (5) z11=x11-y1r (6) zi=xi-αi-1,i=2,…,n (7) 注2与基于BLF的控制方法不同[29-30],本文设计了一种新颖的坐标变换公式(5)~公式(7),分别对系统输出x1与跟踪误差y进行约束。 考虑如下Lyapunov函数 (8) (9) 设计虚拟控制器αi,i=1,…,n-1和控制律u为 (ρ1+z1)(ρ2-z1)×(x1-k1)(k2-x1))) (10) (11) (12) (13) 公式中:ω=(k2-k1)(ρ1+z1)(ρ2-z1)+(ρ1+ρ2)(x1-k1)(k2-x1);ci,i=1,…,n为正的设计常数。对虚拟控制器αi-1,i=2,…,n求导,则有 (14) 根据等公式(1),公式(5)~公式(7),公式(10)~公式(14),可得 (15) (16) (17) (18) 最后,对Vn求导,将公式(15)~公式(18)代入公式(9)可得 (19) 定理1考虑由系统(1),虚拟控制器(10)~(12),控制律(13)组成的闭环系统.若假设1成立,且初始条件满足k1 1)闭环系统所有信号有界; 2)系统输出满足给定的约束条件(2); 3)跟踪误差z1符合预先设定的性能要求,即-ρ1 4)limt→∞z1=0。 (20) 公式中:ξ=ρ1(k2-x1)(yr-k1)+ρ2(x1-k1)(k2-yr)+ρ1ρ2(k2-k1),注意到ξ>0,故limt→∞z1=0。 -b1 (21) 则可推得系统输出x1(t)满足给定的约束条件,即 -k1<-b1+yr (22) 然而,(22)也隐含着初始条件x1(0)须满足 -k1+A0+yr(0) (23) 即x1(0)必须限制在一个比给定约束条件Ω更小的区域内,这使得该方法具有较大的保守性。与基于BLF的控制方法不同[16-18,29,30],本文所提控制算法采用新的坐标变换(5)~(7)直接对系统输出进行约束,即初始条件x1(0)应满足 -ρ1(0)+yr(0) (24) 设置预设性能函数的初始值满足以下条件: -ρ1(0) (25) 能确保以下不等式成立 yr(0) (26) 即x1(0)适用于在给定约束条件Ω区域内的任何值,避免了BLF引起的保守性问题。此外,性能函数ρ1,ρ2不依赖于系统的输出约束条件(2),增大了其选取的灵活性。 在本节中,我们用两个仿真来测试本文控制策略的有效性和实用性。第一个仿真是将本文控制方法与基于BLF的控制方法对比;第二个仿真是将该控制方法应用于实际系统中。 例1:考虑如下一类二阶非线性系统 (27) 公式中:系统初始值设置为[x1(0),x2(0)]T=[0.4,0.1]T;参考轨迹yr=0.2+0.4cos(t);约束常数k1=-0.8;k2=0.8,控制器参数c1=1,c2=2;性能函数ρ1=2e-0.5t+0.01,ρ2=e-0.3t+0.01。仿真结果如图1和图2所示。图1和图2分别为输出跟踪性能和控制信号u。从图1可以看出,在本文所提控制策略下,系统输出y满足给定的约束条件k1 图1 输出跟踪性能Fig.1 Output tracking performance 图2 控制信号uFig.2 Control signal u (28) (29) 其中,b1=k2-A0=0.2。仿真结果如图3和图4所示。图3和图4分别为采用BLF的控制方法时的输出跟踪性能和控制信号u。从图3和图4可以看出,该控制策略在时间0.05 s-0.06 s时失效,根据公式(23)计算可知,x1(0)的适用区间为(0.4,0.8),在本次仿真中初始状态所设值x1(0)=0.4,在适用区间外,所以控制器失效。对比本文的控制方案中初始条件x1(0)只需满足给定的约束条件k1 图3 BLF输出跟踪性能Fig.3 BLF output tracking performance 图4 BLF控制信号uFig.4 BLF control signal u 例2:为了测试所开发的控制策略的实际应用,考虑了一个倒立摆系统,其动力学模型可以表示为[33] (30) 其中 公式中:x1和x2分别为钟摆的角位移和角速度;g=9.8 m/s为重力加速度系数;Mc和Mp分别为小车和杆子的质量;L为杆的半长;u为施加的力控制;Mc=1.0 kg;Mp=0.1 kg;L=0. 5m。初始状态[x1(0),x2(0)]T=[3,2]T,控制目标是使y=x1跟踪yr=3+sin(t);约束常数k1=1,k2=5,控制器参数c1=1,c2=2,性能函数ρ1=2e-0.5t+0.01,ρ2=3e-0.3t+0.01,仿真结果如图5和图6所示。图5和图6分别为输出跟踪性能和控制信号u。从图中可以看出,在本文所提控制策略下,系统输出y满足给定的约束条件k1 图5 角位移输出跟踪性能Fig.5 Angular displacement output tracking performance 图6 力控制信号uFig.6 Force control signal u 本文研究了一类含有输出约束的严格反馈非线性系统的预设性能控制问题.结合系统的输出约束条件与预设性能要求,设计了一种新颖的坐标变换.与基于BLF的控制方法不同,本文采用坐标变换直接对系统输出与跟踪误差进行约束,避免了BLF引起的保守性问题.此外,性能函数不依赖于系统的输出约束条件,增大了其选取的灵活性.仿真结果验证了该控制方案的有效性和实用性.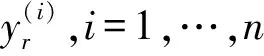
2 控制器设计

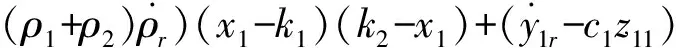
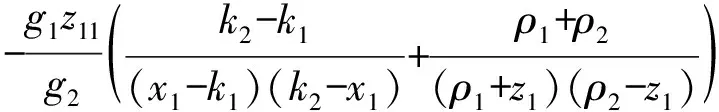
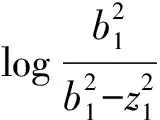
3 仿 真

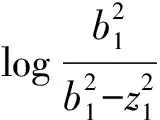



4 结 论

