解答数学题的四个常规步骤
周佳琦


数学家波利亚在《怎样解题》中对怎样解题进行了深入而又细致的分析与讨论,并提出在解题过程中所需要经历的四个阶段,第一阶段:理解题目,看清题目中的要求是什么;第二阶段:掌握题目中所涉及的相关项目是如何关联起来的,已知量与未知量之间具有什么样的关系;第三阶段:执行所设计的方案;第四阶段:回顾解题的过程并进行检查与讨论.仔细研究可发现,这就是解题的四个步骤:审题——寻找解题思路——确定解题方案并实施——检验解题过程.
解题的第一步是审题.我们需要仔细读题,明确题意:
(1)弄清楚题目中给出的已知条件以及所求的目标;
(2)确定哪些是已知量,哪些是未知量,隐含条件有哪些;
(3)判断所给的条件充足与否;
(4)判断题目属于什么类型;
(5)明确涉及了哪些知识点;等等.
第二步,需要在找出有用的数据和信息后,将其关联起来,仔细分析问题,寻找解题的思路.最重要的是确定题目中的未知量与已知量之间的关系,并将其关联起来,可用相关的公式,引入辅助元,构造辅助数列,用已有的知识与过去的解题经验,寻找解题的思路.
第三步,确定并实施解题方案.这一步是解题的关键,需要对上一阶段中所确定的解题思路进行分析、整理、优化,可画出相应的表格、图象,以辅助解题.在这个过程中,需确定解题的每一个步骤,列出关系式、建立数学模型,根据已知条件、相关定理、公式、性质、运算法则进行推理、运算,确保推理有理有据,计算准确,解题的过程简洁、有条理,答案正确.
第四步,检查上一阶段中得到的解题过程,并进行验算,主要检查:
(1)运用到的公式、定义、性质是否正确;
(2)运算过程是否正确;
(3)用到的数据是否正确;
(4)图表是否正确.若存在错误,需及时改正.对于解题或证明过程相对繁杂的题目,这一步尤为重要.在该过程中,要对题目进行反复斟酌,并对所获得的解题过程进行回顾,以确定得到答案的正确性.
[C. 以MN为直径的圆与l相切]
[D. ΔOMN为等腰三角形]
分析:题目中的已知量有:
④直线[l]为抛物线C的准线.
未知量有:①[ p]的取值;
②线段|MN|的长度;
③以MN为直径的圆与直线[l]的位置关系;
④[ΔOMN]的形状;
解题思路:由抛物线的焦点坐标可以确定[p]的取值;由直线MN的倾斜角与圆锥曲线的定义可以确定线段|MN|的长度;通过图象可以研究以MN为直径的圆与直线[l]的位置关系,判断出[ΔOMN]的形状.这样便将未知量与已知量关联起来了.
本题的解答过程为:
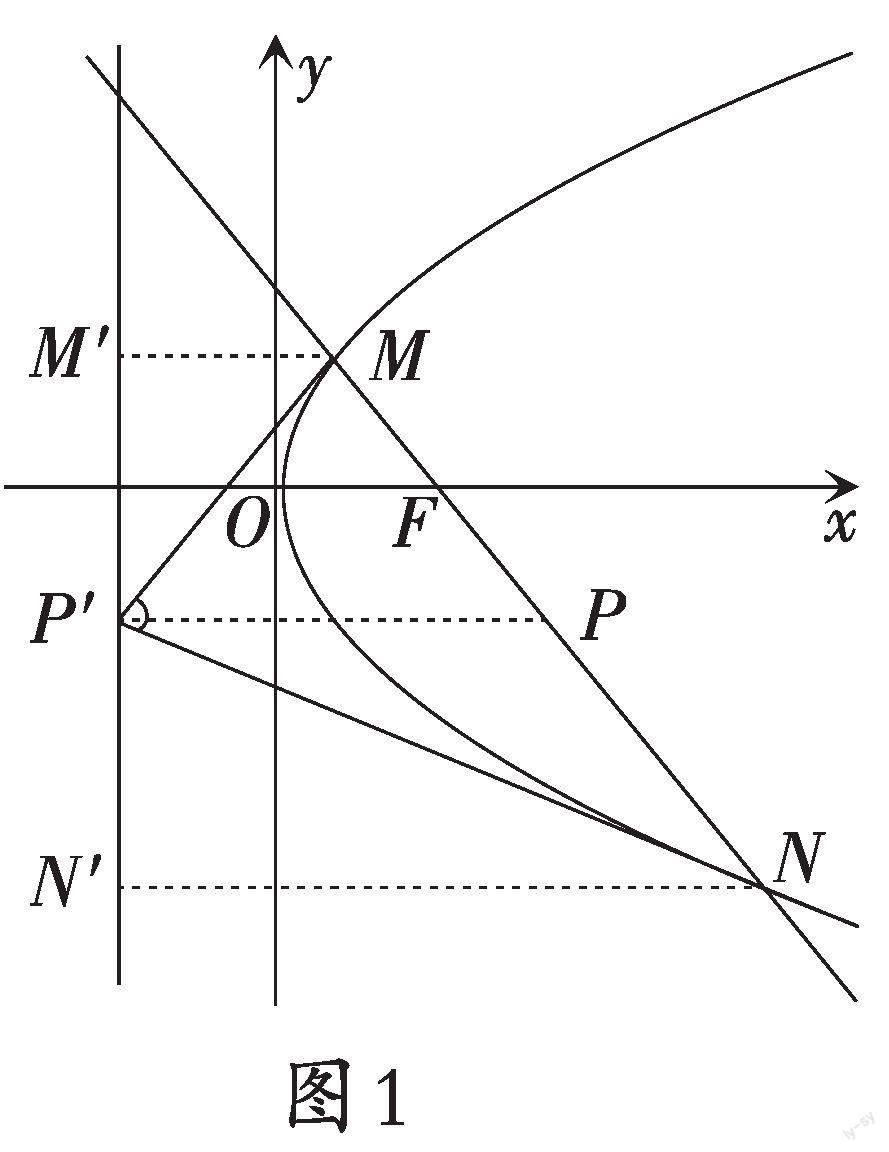
根据题设条件画出圆锥曲线的图象,如图1所示.由抛物线的定义可知,焦点[F]的横坐标为1,则[p=2],故A选项正确;
过点[M]作准线[l]的垂线,交[l]于点[M];过点[N]作准线[l]的垂线,交[l]于点[N];取[MN]的中点为[P],过点[P]作准线[l]的垂线,交[l]于点[P],连接[MP]、[NP],
由抛物线的定义知[|MF|=|MM|],[|NF|=|NN|],
所以[|MN|=|MM|+|NN|].
即[|PP|=|MP|=|PN|],
所以以[MN]为直径的圆与直线[l]相切,故[C]选项正确;
通过观察图象可知,[ΔOMN]不是等腰三角形,故[D]选项错误;
所以本题的答案为[AC].
经检验,所得的结果正确.
(1)求[C]的方程;
(2)记[C]的左、右顶点分别为[A1,A2],过点[B(-4,0)]的直线[l]与C的左支交于[M,N]两点,[M]在第二象限,直线[MA1]与[NA2]交于[P],证明:[P]在定直线上.
分析:题目中的已知量有:
①该圆锥曲线是以中心为坐标原点的双曲线;
④直线[l]过定点[B(-4,0)];
⑤点[P]为直线[MA1]与[NA2]的交点;
未知量有:①双曲线[C]的方程;
②点[P]是否在定直线上.
解题思路:通过已知的[a,e]的取值,结合双曲线的定义,就可以确定双曲线的方程;依题意可知,直线[l]过定点[(-4,0)],可以令直線[l]为[x=ty-4].另外,结合(1)可以得出点[A1,A2]的坐标,设[M(x1,y1),N(x2,y2),P(x0,y0)],就可以得出直线[MA1]与[MA1]方程,接着联立方程,即可得解.
解答本题的过程为:
根据题设条件画出圆锥曲线的图象,如图2所示.
解得[x0=-1],所以点[P]在定直线[x=-1]上.
经检验点[P]在定直线[x=-1]上,且满足题意.
很多同学在解题时常常不清楚应该如何下手,由哪个地方切入,掌握了解题的这四个步骤,就能高效、正确的完成解题.审题、寻找解题思路、确定并实施解题方案、回顾或检查解题的过程,每一个步骤都不可或缺,并有一定的先后顺序,上一个阶段是下一个阶段的前提,下一个阶段是对上一个阶段的完善.这四个步骤虽然不一定适用于所有的题目,却能为同学们解题提供一个大致的方向,这有利于培养同学们良好的解题习惯,进而提高解题的效率.

