基于动态广义正交模糊集的多属性决策方法
柳晓燕,张晨雪,李小南,冯 锋
(1.西安邮电大学 理学院,陕西 西安 710121; 2.西安翻译学院 信息工程学院,陕西 西安 710105; 3.西安电子科技大学 数学与统计学院,陕西 西安 710126)
随着时间的推移,人们在社会经济活动中面临着越来越复杂的决策问题。决策中涉及的不确定因素不断增加,导致处理决策问题所需要的知识在深度和广度上也随之提升[1]。经典多属性决策理论不能有效地刻画实际决策过程中的复杂性和不确定性,使得现代决策科学愈发重视和发展处理不确定性问题的数学理论和模型,并用其来解决复杂的决策问题。面对这一挑战,Zadeh[2]在1965年提出了模糊集的概念,以程度化的方式表达和处理不确定性。在处理更复杂的问题时,往往需要从正反两方面进行考虑,Atanassov为此于1983年提出了直觉模糊集[3]。Xu和Yager[4]将直觉模糊集中各元素的隶属度和非隶属度组成的序对称为直觉模糊数。2013年,Yager[5]松弛了隶属度和非隶属度的约束条件,定义了毕达哥拉斯模糊集,并应用于解决实际决策问题。随后,Yager[6]再次推广了毕达哥拉斯模糊集的定义,提出了广义正交模糊集。广义正交模糊集满足隶属度的q次方与非隶属度的q次方之和不超过1,扩展了直觉模糊集和毕达哥拉斯模糊集的适用范围,在实际应用中更加灵活方便。
自广义正交模糊集问世以来,很多学者研究了基于广义正交模糊集的多属性决策方法。在广义正交模糊决策研究中,广义正交模糊数的比较、排序和集结方法发挥了核心作用。广义正交模糊数的排序方法可以归结为两类:第一类,根据得分函数[7]和精确函数[8]进行排序;第二类,根据基于几何表示的方法[9-15]进行排序。杜文胜[9]研究了广义正交模糊数的Minkowski距离,并给出了相关排序方法。在广义正交模糊信息集结方面,卫贵武等[16]研究了广义正交模糊数的广义海伦平均算子和几何海伦平均算子,并对其相关性质进行了研究。王军等[17]提出了广义正交模糊Maclaurin对称平均算子和广义正交模糊加权Maclaurin对称平均算子。杜文胜[18]提出了广义正交模糊数的算术运算,并研究了一些相关性质。在文献[19]中,杜文胜又提出了广义正交模糊加权幂平均算子和广义正交模糊有序加权幂平均算子,对其基本性质进行了详细的研究,并将其应用于解决多属性决策问题。
在实际决策问题中,备选方案往往处于动态变化中,需要考虑备选方案在不同时间段内的动态表现并进行综合决策。但经典多属性决策方法仅能对当前状态下的备选方案进行评价和排序,具有一定的局限性。为此,学者们将静态的经典多属性决策问题向动态方向拓展,提出了动态多属性决策,在理论深度和应用广度上极大地丰富了多属性决策研究。一些学者将逼近理想解排序法[20-22](Technique for Order Preference by Similarity to Ideal Solution,TOPSIS)和多准则妥协解法[23-24](VIseKriterijumska Optimizacija I Kompromisno Resenje,VIKOR)等传统决策方法扩展应用到动态多属性决策中,在这些研究中集结算子和权重确定方法至关重要。在集结算子研究方面,Xu和Yager[20]提出了动态直觉模糊加权平均(Dynamic Intuitionistic Fuzzy Weighted Averaging,DIFWA)算子,并结合基于Minkowski距离的TOPSIS法研究了动态直觉模糊多属性决策方法。权重的确定方法包括属性权重和时间权重两方面:属性权重客观确定方法包括离差最大化法[25]、熵权法[26-27]和主成分分析法[28]等;时间权重确定方法[29]包括基本单位区间单调(Basic Unit-interval Monotonic,BUM)函数法、正态分布法和指数分布法等。此外,部分学者认为集结过程会造成信息损失,通过构建评价模型[30-31]进行综合计算,以此解决动态多属性决策问题。
目前,现有文献中对广义正交模糊环境下的动态多属性决策方法鲜有探索。为此,拟着重关注动态广义正交模糊集及其在动态多属性决策中的应用。首先,给出动态广义正交模糊集及其基本运算的定义。然后,在动态广义正交模糊环境下探索决策信息的集结问题,提出一种动态广义正交模糊多属性决策方法。最后,将所提决策方法应用于5G通信企业评估问题,并通过对比分析验证其合理性。
1 预备知识
模糊集、直觉模糊集、毕达哥拉斯模糊集、广义正交模糊集及其运算等基础知识概述如下,若无特殊说明,论域均表示为U。
1.1 模糊集与毕达哥拉斯模糊集
定义1[2]映射μ:U→[0,1]称为论域U中的一个模糊集。表示模糊集的映射μ称为隶属函数,称μ(u)为u对于μ的隶属度,用于量化u属于μ的程度。
定义2[3]论域U上的直觉模糊集定义为
I={(u,tI(u),fI(u))|u∈U}
式中:映射tI:U→[0,1]和fI:U→[0,1]分别称为I的隶属函数和非隶属函数;函数值tI(u)和fI(u)分别称为u对于I的隶属度和非隶属度,且满足0≤tI(u)+fI(u)≤1。
定义3[5]论域U上的毕达哥拉斯模糊集定义为
P={(u,tP(u),fP(u))|u∈U}
1.2 广义正交模糊集
定义4[6]论域U上的广义正交模糊集定义为
G={(u,tG(u),fG(u))|u∈U}

定义5[6]论域U上的广义正交模糊集
A={(u,tA(u),fA(u))|u∈U}B={(u,tB(u),fB(u))|u∈U}
的交、并、补运算分别定义为
A∩B={(u,min{tA(u),tB(u)},max{fA(u),fB(u)})|u∈U}A∪B={(u,max{tA(u),tB(u)},min{fA(u),fB(u)})|u∈U}A′={(u,fA(u),tA(u))|u∈U}
定义6[6]设

其中,(a1,a2)和(b1,b2)为广义正交模糊数。
广义正交模糊数的一些基本运算定义如下。
定义7设A=(a1,a2)和B=(b1,b2)是广义正交模糊数,若λ为任意正实数,则有
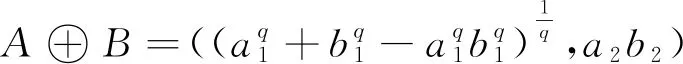
2 动态广义正交模糊集
设GOFSq(U)表示U上全体广义正交模糊集构成的类。将(U,T)称为动态论域,其中T是与U中对象关联的所有时间参数构成的集合,称为时域空间。应当注意,即使U是有限集时,T也可以是一个无限集。
定义8二元组I=(ω,A)称为论域U上的一个动态广义正交模糊集,其中A⊆T称作I的时间参数集,映射ω:A→GOFSq(U)(q≥1)称为I的动态近似函数。
通过引入时间参数,动态广义正交模糊集给出了动态不确定概念在不同时刻的静态近似描述。对任意的t∈A,称ω(t)∈U为I的t-近似元集。
为了更好地描述和处理广义正交模糊环境下的动态决策问题,下面将广义正交模糊集的运算进行动态扩展。
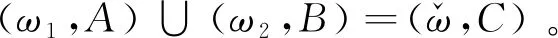
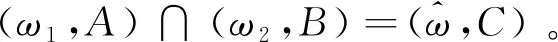

定义12设I=(ω,A)是论域U上的一个动态广义正交模糊集,λ为任意正实数。λ和I的标量积为一个动态广义正交模糊集Ω=λI=(θ,A)。∀t∈A和∀u∈U,Ω的动态近似函数θ定义为

(1)

3 动态广义正交模糊多属性决策
3.1 动态广义正交模糊信息集结方法
定义13设(P1,≤1)和(P2,≤2)为两个偏序集,P1×P2上的字典序定义为
(a1,b1)≤(a2,b2)⟺(a1<1a2)∨(a1=a2∧b1≤2b2)
其中,(a1,b1),(a2,b2)∈P1×P2。
下面将文献[32]中直觉模糊数的字典序定义推广至广义正交模糊数的范畴,具体如下。
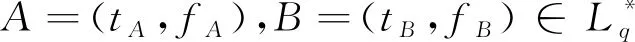
(2)
在广义正交模糊决策中,集结算子可将一组输入数据融合为一个输出数据,其定义如下。
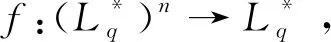

条件2f(a1,a2,…,an)=(0,1),其中ai=(0,1) (i=1,2,…,n)。
条件3f(a1,a2,…,an)=(1,0),其中ai=(1,0) (i=1,2,…,n)。
条件1a1≤b1∧…∧an≤bn⟹
f(a1,a2,…,an)≤f(b1,b2,…,bn)
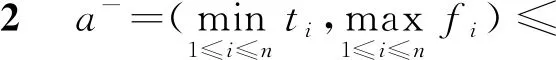
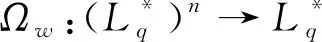
Ωw(a1,a2,…,an)=w1a1⊕w2a2⊕…⊕wnan

根据定义17,用数学归纳法可证关于GOFWA算子的如下结论。
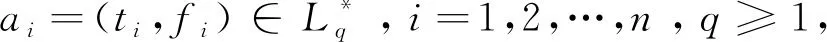
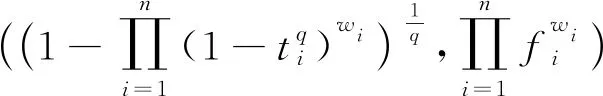
(3)
其中,w=(w1,w2,…,wn)T是权重向量。
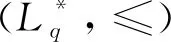
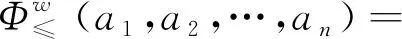

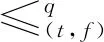


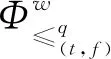
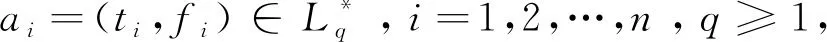

(4)
其中,w=(w1,w2,…,wn)T是算子权重向量。
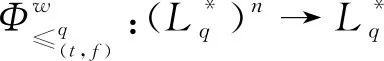
证明根据定义16,分别证明以下两个条件。
条件1考虑算子集结后仍是一个广义正交模糊数,分别令

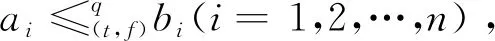
设共有k组ai和bi满足ti 情况1若k≠0,则tσ(i)≤uσ(i)(i=1,2,…,n)(当k=n时,有tσ(i) 于是, 因此, 情况2若k=0,则tσ(i)=uσ(i)∧fσ(i)≥vσ(i)。类似情况1中的推导过程,可得 条件2根据广义正交模糊数的交与并的定义,分别令 再根据其单调性可得 其中, 且i=1,2,…,m,j=1,2,…,n,k=1,2,…,l。 由定义20和定理2,可以证明如下结论。 定理4设I=(ω,A)是动态有序加权平均广义正交模糊集,则可计算其动态近似函数 ω(tj)(ui)= (5) 其中, 其中,q≥1且i=1,2,…,m。 由定义21和定理1,可证如下结论。 定理5给定论域U={u1,u2,…,um}上一个动态广义正交模糊集I=(ω,A),其中时间参数集A={t1,t2,…,tn},且 (6) (7) 考虑到不同时间段内,不同属性的重要程度也会随之变化,因而应给不同时间段的属性不同的权重值。为此,下面采用文献[25]中的最大偏差法确定属性权重。属性评价值均为广义正交模糊数,选择常用的汉明距离度量偏差。两个q阶广义正交模糊数a=(a1,a2)和b=(b1,b2)之间的汉明距离为 (8) 在tj(j=1,2,…,n)时刻属性ek(k=1,2,…,l)下所有备选方案的属性评价值的偏差之和为 (9) 如果每个备选方案的评价值在某个属性下偏差和较小,即几乎没有差异,则表明该属性在方案排序过程中的作用较小,应被赋予较小的权重;相反,如果某个属性的评价值偏差和较大,则该属性在方案排序中有重要作用,应分配较大的权重。在此仅考虑属性权重信息完全未知的情况,根据上述思想,即求解优化模型获得属性权重,优化模型为 (10) 而后将求得的属性权重进行归一化,即可得到属性权重 基于广义正交模糊集的多属性决策方法中,阶数q大多采用了直接指定的处理方式。这种方式依赖于决策者的主观判断,会在一定程度上对决策结果的客观性产生影响。如何给出确定阶数的合理方法是一个重要问题。Riyahi等提出了一种确定广义正交模糊集的合理阶数的基本策略[34]。借鉴文献[34]中的思想,下面给出一种简便方法,以便在实际应用中确定动态广义正交模糊集的阶数q。 设I=(ω,A)是论域U上的动态广义正交模糊集,A为时间参数集。记 ω(a)(u)=(tω(a)(u),fω(a)(u)) 其中,a∈A且u∈U。令 (11) 当阶数q满足条件Mq+Mq≤1时,I中所有广义正交模糊数均可满足对应的约束条件。由此可得 (12) 为降低幂运算造成的信息损失,实际应用中可选取使上式成立的最小正整数作为动态广义正交模糊集的最优阶数。 I(k)=(ω(k),T) (k=1,2,…,l) 记其动态近似函数为 基于GOFOWA算子的动态广义正交模糊多属性决策方法的流程如图1所示,具体步骤如下。 图1 动态广义正交模糊决策方法流程 步骤1根据给定的动态决策信息在论域U上建立l个动态广义正交模糊集 步骤2将属性集合E按照效益型属性和成本型属性划分为两个不相交的子集Eb和Ec。 步骤6给定广义正交模糊有序加权平均算子的算子权重w=(w1,w2,…,wl)T。 步骤8利用时间熵最大化方法确定时间权重向量η=(η1,η2,…,ηn)T。 运用数值实例与现有方法进行比较,验证所提动态广义正交模糊多属性决策方法的合理性。 5G是第五代移动通信技术的简称,其并不是一种独立的、全新的无线接入技术,而是现有无线接入技术(包括2G、3G、4G和WiFi)的演进,以及通过集成一些新的互补无线接入技术形成的解决方案的总称[35]。与传统的通信技术相比,5G是一种将多种通信技术相结合的综合性新技术,具有速度快、流量密度高、时延短、能效高、支持海量连接及增强移动宽带等诸多优点。5G技术优势显著,其将带动多行多业的发展,且具有非常广阔的应用前景。运营商选择5G通信企业合作伙伴时,会先从多个方面对企业的5G通信产品进行评估,再综合各项评价给出最优选择。在此过程中,需要有合理、可靠的评估指标为决策过程提供支持,以保证决策结果的科学性和可用性。 选用文献[35]中的e1、e2、e3、e4和e5等5个指标作为评估的关键因素,其中:e1表示峰值数据速率,描述了最大可实现数据速率;e2表示用户体验的数据速率,描述了覆盖区域可实现数据速率;e3表示区域流量容量,描述了覆盖区域总流量;e4表示能量效率,描述了每单位能耗发送/接收的数据;e5表示延迟,描述了数据包在网络中传输的延迟时间。 设论域U={u1,u2,…,u5},其中ui(i=1,2,…,5)分别代表三星、中兴、爱立信、华为及诺基亚。某运营商计划从这5家领先的5G企业中选择一家进行合作。将上述5个指标构成的属性集记作E={e1,e2,e3,e4,e5},时域空间记为T={t1,t2,t3},并取时间参数集A=T。专家将从t1(2018年)、t2(2019年)和t3(2020年)等3个时段依照上述5个评价指标对待选企业进行评估。根据指标含义,指标e1、e2、e3、e4均为效益型属性,指标e5为成本型属性。专家打分通过转换处理后均以广义正交模糊数的形式量化,如表1所示。 表1 动态广义正交模糊集 利用所提动态广义正交模糊多属性决策方法求解步骤如下。 步骤2将属性集合E按照效益型属性和成本型属性划分为两个不相交的子集Eb={e1,e2,e3,e4}和Ec={e5}。 表2 动态广义正交模糊集I(5)=(ω(5),T) 步骤4根据式(12)分别求出动态广义正交模糊集I(k)(k=1,2,3,4,5)的最优阶数分别为 步骤5根据式(8)和式(9)求得在tj时刻属性ek下所有待选企业之间决策信息评估值的偏差之和分别为 将上述结果代入式(10)求解优化模型 求得的权重向量分别为 经过归一化处理后,分别得到tj(j=1,2,3)时刻下的3个属性权重向量分别为 w(1)=(0.073 6,0.108 2,0.037 5,0.093 4,0.687 4)Tw(2)=(0.326 5,0.077 5,0.027 9,0.125 9,0.442 2)Tw(3)=(0.023 2,0.282 8,0.022 5,0.052 6,0.618 9)T 步骤6取态度特征值为0.1,计算可得GOFOWA算子的算子权重为 w=(0.347,0.277,0.214,0.124,0.038)T 2)将5个加权动态广义正交模糊集Ω(k)=(θ(k),T)中的广义正交模糊数进行排序,使 成立,其中i=1,2,…,5,j=1,2,3,k=1,2,3,4,5,且(σ(1),σ(2),…,σ(5))为(1,2,3,4,5)的一个置换。 3)根据定义20和式(5),利用算子权重w=(w1,w2,w3,w4,w5)T将置换后得到的5个加权动态广义正交模糊集集结为1个动态有序加权平均广义正交模糊集I=(ω,T),如表3所示。 表3 动态有序加权平均广义正交模糊集I=(ω,T) 步骤8假设决策者在各时段数据中较重视近期数据,根据文献[33]中时间度的标度参考表,取时间度λ=0.3,根据式(7)求解非线性规划模型 可得到时间权重向量为η=(0.15,0.30,0.55)T。 步骤9根据定义21和式(6),由η和I求得时间加权平均广义正交模糊集分别为 G(u1)=(0.356,0.901)G(u2)=(0.560,0.868)G(u3)=(0.311,0.919)G(u4)=(0.581,0.868)G(u5)=(0.473,0.904) u4≻u2≻u5≻u1≻u3 根据偏好排序结果给出决策建议,在当前决策环境下,建议选择的合作企业是华为。 为了研究阶数q对方法结果的影响,现保持上述其余变量不变,仅改变阶数q的取值,所得排序结果如表4所示。 表4 不同阶数q下的排序结果 从表4排序结果可见,q=3时的排序与其余结果存在些许差异,而由式(12)所确定范围内的阶数q对应的排序结果完全一致,这表明3.2节中所提最优阶数的确定方法是合理的。 各种方法所得排序结果如表5所示。 表5 不同决策方法的结果比较 由表5中的排序结果可见,所提方法与文献[20]和文献[21]中动态多属性决策方法给出的排序结果基本一致,u4和u2在排序中均处于前两位,u3均处于最末位。排序结果存在微小差异的原因在于文献[20]和文献[21]使用直觉模糊集或毕达哥拉斯模糊集描述决策信息,而4.2节中的部分数据并不满足直觉模糊集或毕达哥拉斯模糊集的约束条件。所提方法先结合属性权重计算加权动态广义正交模糊集,然后综合考虑各个时刻对备选方案整体评价的影响,且评价信息的表示由直觉模糊集或毕达哥拉斯模糊集扩展为动态广义正交模糊集,扩大了相关决策方法的应用广度和深度。 文献[9]中方法基于Minkowski距离计算备选方案的贴近度(即备选方案远离负理想且接近正理想的程度)并给出方案排序。参数p不同时,分别对应汉明距离(p=1)、欧几里得距离(p=2)和切比雪夫距离(p=∞),对应排序结果略有差异。由于文献[9]方法并未考虑时间因素的影响,其排序结果与上述方法相比差别较大。文献[35]在毕达哥拉斯模糊环境下扩展了CoCoSo多属性决策法,该方法与所提方法的排序结果基本一致,均认为u4是最优方案,u3是最劣方案。与文献[9]和文献[35]相比,所提方法考虑了时间因素对决策过程的影响,能够捕捉不同时刻决策信息的变化,从而做出更符合实际情况的科学决策。 考虑到在实际决策环境中,备选方案在不同时刻的重要性往往处于动态变化之中,因此,对广义正交模糊集进行动态扩展,定义了动态广义正交模糊集及其基本运算。利用动态广义正交模糊集和广义正交模糊有序加权平均算子,提出了动态广义正交模糊环境下的一种多属性决策方法。该决策方法考虑了时间因素对决策过程的影响以及不同时间段内决策信息的重要程度,充分反映了专家对备选方案的总体评价随时间变化的特点。最后,通过5G通信企业评估问题验证了所提方法的有效性,并与现有几种方法进行了对比分析,结果表明,基于动态广义正交模糊集的多属性决策方法考虑了时间因素对决策过程的影响,能够动态捕捉不同时刻决策信息的变化,从而做出更符合实际情况的科学决策。 上述研究仅将动态广义正交模糊集与GOFOWA算子进行结合,今后可尝试将其他算子与动态广义正交模糊集相结合,提出更符合实际应用需求的动态多属性决策方法。
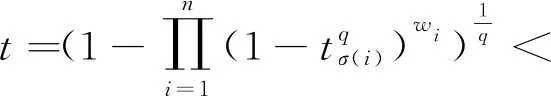
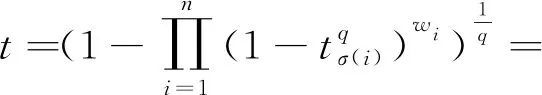
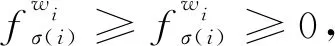
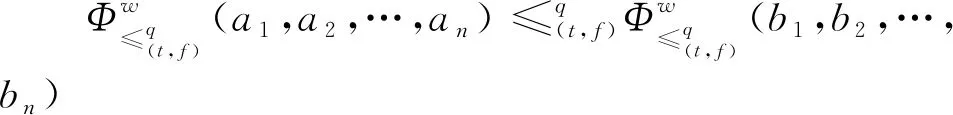
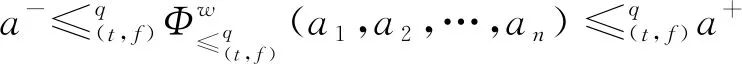
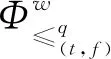

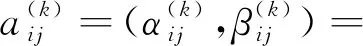
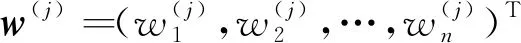

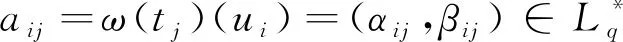
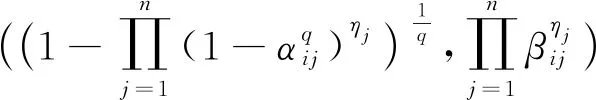
3.2 动态广义正交模糊多属性决策方法



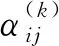
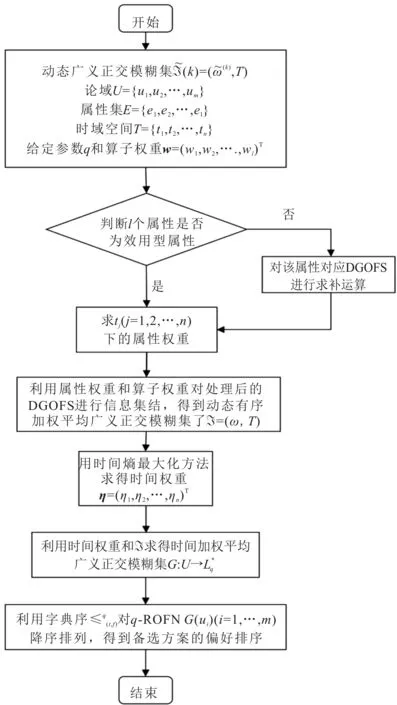
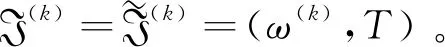
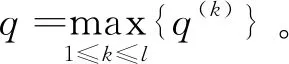
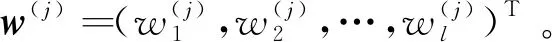
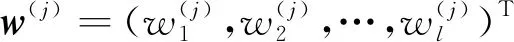

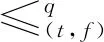
4 算例分析
4.1 5G通信企业评估问题
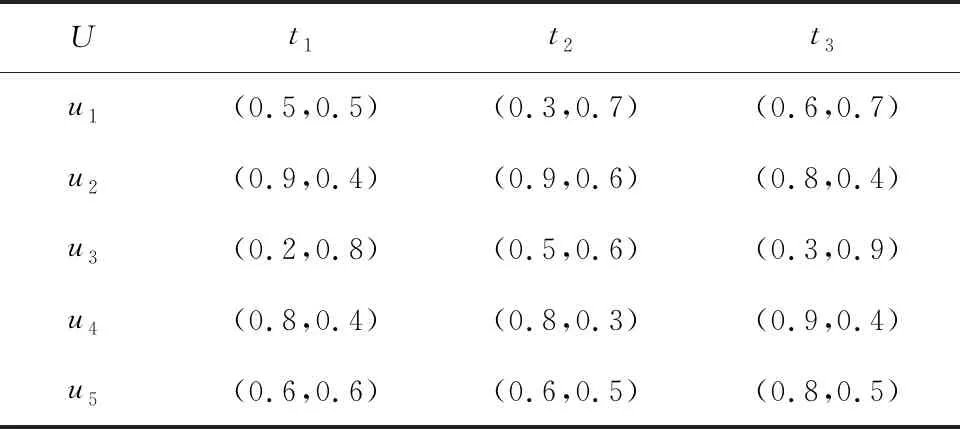
4.2 问题求解
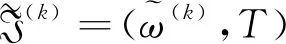

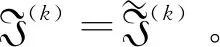
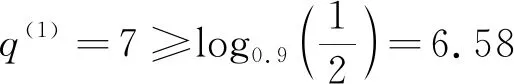

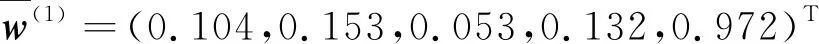
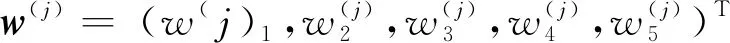






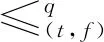

4.3 对比分析
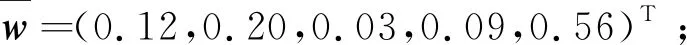

5 结语

