具有输出约束的多机械臂系统模糊控制器设计
范永青,张占磊
(西安邮电大学 自动化学院,陕西 西安 710121)
机械臂是一种通过程序移动并操控机械手进行抓/放操作的装置。随着计算机的发展,机械臂被应用在生态系统监测[1]、航空航天[2]和医学工程[3]等工程领域。机械臂作为机器人系统中的重要组成部分,可以执行工业装配、安全防爆和医疗协助等工作。目前,对机械臂的研究主要集中在作用任务物体时实现精准的控制。文献[4]通过采用人机接口,提出了一种精确搬运物体的控制方法。文献[5-6]指出在不受外界因素影响的条件下,虽然精确校准过的机械臂也能够确保控制过程中系统的稳定性,但当外部环境和设备磨损、电流波动及信号延迟等内部参数变化时,系统的控制性能通常是不稳定的,这使得校准过的系统运动适应性较差。同时,机械臂系统的工作场景往往是高度非线性的,如在工程应用中,当机械臂抓取多个不同尺寸的物体时,机械臂的动力学参数会发生较大的变化,因此这类系统被称为动力学方程未知的机械臂系统。为了使机械臂广泛应用于非线性的工作场景,研究动力学方程未知的机械臂系统成为实现精准控制的一个重要内容。
在动力学方程未知的机械臂系统中,为解决非线性问题,常用的方法有模糊逻辑系统(Fuzzy Logic System,FLS)和径向基函数,其中FLS中的推理机制能够将某些知识转化成人类能力,如学习、适应、容错和并行[7-8]。根据这一特性促使许多研究者提出了用于处理不确定性的有效自适应控制器[9-10]。但是,FLS的万能逼近原理[11]只适用于一些特定的域内,如果系统状态超出该域,自适应控制的能力将会减弱,只能保证系统状态半全局一致最终有界(Semi-Globally Uniformly Ultimately Bounded,SGUUB)。对于局限于特定域内的机械臂而言,设计不受定义域所约束的通用控制器更能符合实际工业中的需要。例如,当未知函数的状态扩展到FLS域外时, Hwang[12]设计了一种模糊自适应方法实现全局渐近跟踪稳定,但该方法通过FLS逼近未知非线性项时需要大量的模糊规则。为了减少模糊规则产生庞大的在线计算量,文献[13]提出了一种具有少量规则的全局自适应模糊一致性控制器,这种控制方法能保证系统中的所有信号一致最终有界(Uniformly Ultimately Bounded,UUB),并可以减轻具有不确定性的一阶和二阶多智能体系统的计算负担。在文献[12-14]中,指出全局自适应控制方法通常适用于某些类型的结构系统,如移动机械臂和单输入单输出非线性系统,在针对较复杂的被控系统时,设计一种不仅具有少量模糊规则,还能有较高逼近精度的全局模糊自适应控制器更具广泛性。
机械臂的研究可分为关于单机械臂与多机械臂的研究,在处理分拣、搬运小型物体等过程中,单机械臂的系统就能够实现,还可以降低硬件成本。但是,在处理需要协调操作及搬运大型物体的任务时,达不到多机械臂系统的控制效果,因此多机械臂的协调控制研究受到广泛关注[15-16]。文献[17]提出了一种半分散模糊自适应控制方法,用于多机械臂在运动和内力跟踪下的协作问题。Yang等[18]使用近似雅可比矩阵估计双臂机器人的模糊控制,其中一些模糊逻辑系统补偿了非线性项的不确定性。对于多机械臂抓取一个共同物体的跟踪问题,设计了一种基于阻抗法的新型分散自适应模糊控制系统[19]。Li等[20]对于多机械臂协作搬运具有阻抗作用的物体时,提出了一种基于合并干扰观测器的分散自适应模糊控制。近年来,对多机械臂携带物体运动问题的研究发现,物体的位置往往会受到空间因素的约束,超出这些约束会导致系统的性能下降,甚至可能导致系统损坏。考虑到被控对象的安全性能,需要对系统的输出进行约束,选择合适的积分障碍李雅普诺夫函数(Integral Barrier Lyapunov Function,IBLF)既能避免违反输出限制,又能使系统不遭到破坏。文献[21]提出了一种具有约束的多机械臂基于模糊神经网络的控制方法,通过 IBLF的稳定条件设计相应的自适应律,保证了系统跟踪误差一致最终有界。在文献[22]中,针对具有输出约束的多机械臂系统,提出了一种自适应神经网络的方法,通过IBLF解决环境限制所产生的约束。因此,在设计具有输出约束的机械臂控制方法时,采用IBLF的稳定性条件能够很好地改善约束问题。但是,这些研究所设计的自适应律数量多,为了减少自适应律的数量,则需要考虑在多机械臂系统研究中加入一个非零时变参数。
针对具有输出约束的多机械臂协调搬运同一物体时轨迹跟踪问题,拟设计一种基于IBLF的模糊自适应控制器。该控制器采用具有非零参数的FLS万能逼近原理估计系统中的非线性项,并通过IBLF的稳定性条件构造能够在线更新的自适应律。当系统状态超出FLS逼近域时,利用滑模控制将域外的状态量拉回到域内,保证闭环系统中的所有信号一致最终有界。为了验证模糊自适应控制器的有效性,在常数约束条件下,将其与自适应控制器和模糊比例微分(Proportional Derivative,PD)控制器进行位置跟踪轨迹对比。
1 系统描述
1.1 机械臂介绍
系统动力学方程需要联立机械臂动力学方程与物体动力学方程,其中第i个n自由度机械臂的动力学方程[23]为
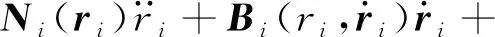
(1)
式中:ri=[ri1,ri2,…,rin]T∈n表示关节位置;n是关节速度;n定义为关节加速度;Ni(ri)∈n×n表示对称正定惯性矩阵;n×n表示科里奥利离心扭矩矩阵;Hi(ri)∈n是关节重力向量;ζi∈n表示控制输入转矩矢量;Γi(ri)∈n×n表示雅可比矩阵;Pi∈n是作用在第i个机械臂末端执行器上的力矢量。
根据式(1),m个机械臂的动力学方程为
(2)
其中,
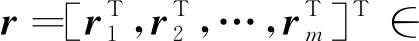
Γ(r)=blockdiag[Γ1(r1),Γ2(r2),…,Γm(rm)]∈(mn)×(mn)N(r)=blockdiag[N1(r1),N2(r2),…,Nm(rm)]∈(mn)×(mn)
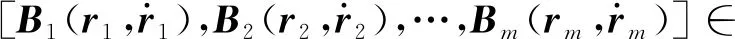
为了将机械臂系统与物体系统联立,需引入物体动力学,其中被搬运的物体动力学[23]方程为
(3)
式中:xo∈n是物体的位置向量;和分别表示物体的速度与加速度;ξ∈n表示m个机械臂的组合力矢量;E∈n是来自未知环境的力矢量,作用于物体的中心;D(xo)∈n×n表示对称正定惯性矩阵;n×n表示科里奥利离心矩阵;W(xo)∈n是重力矢量。
ξ和P之间的关系[23]为
ξ=JT(xo)P
(4)
其中,

式中:Ji(xo)是第i个机械臂末端执行器和物体之间的雅可比矩阵;P可以分解为两个正交分量,其表达式为
P=(JT(xo))+ξ+fI
(5)
式中:(JT(xo))+表示JT(xo)的伪逆矩阵,(JT(xo))+ξ是有助于物体运动的动力矢量;fI指内力矢量,其内力误差是有界的[23],fI在JT(xo)的零空间中满足
JT(xo)fI=0
(6)
考虑被控物体和末端执行器间可能会存在相对运动的情况,但在多机械臂搬运物体过程中暂不考虑柔性的情况,因此得出以下假设。
假设1物体和末端执行器之间不存在相对运动,意味着末端执行器在其工作场中刚性地接触物体。
考虑到xi和ri之间的函数关系,其中xi表示第i个机械臂末端执行器的位置,可得到第i个机械臂关节速度与末端执行器速度之间的关系
(7)
类似地,第i个机械臂末端执行器的速度和物体速度的表达式为
(8)
由式(7)和式(8)可以进一步得到机械臂速度与物体速度之间的关系,表达式为
(9)
为了确保多机械臂工作在非奇异区域,需要假设Γi(ri)的逆矩阵存在,考虑到多个机械臂作用于一个物体,可以得到机械臂关节速度与加速度的表达式分别为
(10)
(11)
将式(10)和式(11)代入式(2),并与式(3)相结合,则机械臂与物体的总动力学方程表达式为
(12)
其中,
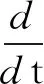
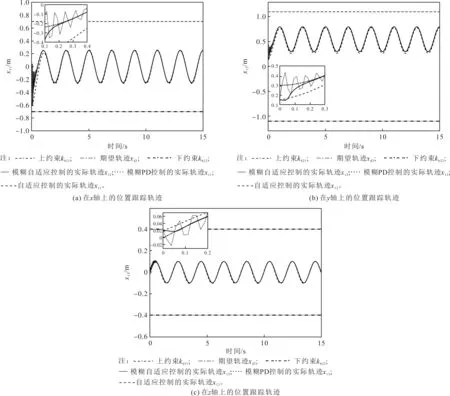
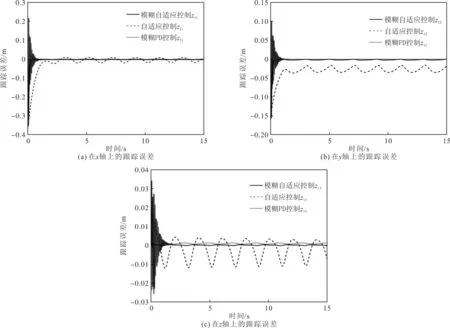
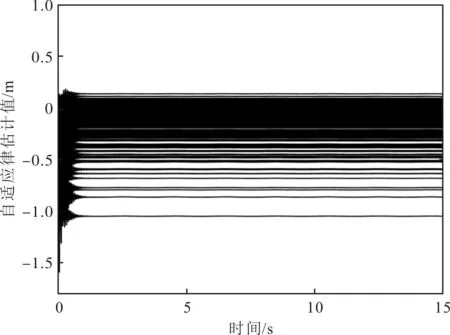
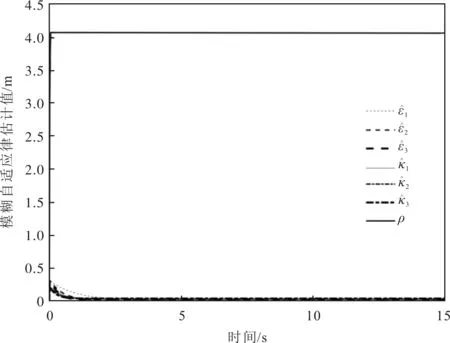
由于不考虑外界环境力的影响,即式(12)中的Fe=0,物体的位置xo=[xo1,xo2,…,xoi]T受常数向量kb=[kb1,kb2,…,kbi]T约束,其中kbi>0,则满足|xoi| 根据式(12),当两个机械臂协作搬运同一物体时,能够按照给出的期望轨迹完成指定的动作,被控物体在笛卡尔空间中跟踪期望轨迹的示意图如图1所示。 图1 两个机械臂作用于一个物体的示意图 性质1式(12)中正定惯性矩阵M与C满足[23] (13) 性质2正定惯性矩阵M满足 λmin(M)‖y‖2≤yTMy≤λmax(M)‖y‖2 (14) 时,条件一致有界[23]。 式中:λmin(M)和λmax(M)分别对应假定的两个已知正常数的最小和最大特征值;‖*‖表示二范数。 在控制工程中,模糊逻辑系统通常用于逼近系统中的未知非线性函数。应用模糊逻辑系统f的万能逼近原理估计未知的连续函数f:s→,Z(t)=[Z1,Z2,…,Zs]T∈s,其中FLS是由IF-THEN规则构造。如果Z1是是是则Y是El,其中:l=1,2,…,Q,Q表示模糊规则的条数;Zi(1≤i≤s)是FLS的输入;表示专家的语言变量。 在应用单值模糊化器、乘积推理和中心平均解模糊器后,FLS估计未知非线性函数的值可以表示为 (15) (16) 为了提高逼近精度与逼近效率,设计了一种具有非零时变参数的FLS万能逼近性质,由此得出引理1。 引理1在紧集U∈n中,对于任何给定具有李普希兹系数κi的连续未知函数Ψi(Z),存在一个FLSFi(Z)满足表示近似误差。然后在紧集中,β是由用户提供的已知正常数,则具有非零参数的万能逼近不等式为 (17) (18) 从引理1的结果可知,通过应用式(15)推导出式(16)的近似精度,表明FLS的输出值可以通过未知非线性函数的非零时变参数ρ和李普希兹系数κi在线更新近似精度。 (19) 式中,x2=[x21,x22,…,x2n]T。 物体的期望轨迹表示为xd=[xd1,xd2,…,xdn]T,于是跟踪误差变量定义为 (20) 式中:z1=[z11,z12,…,z1n]T;z2=[z21,z22,…,z2n]T;c=[c1,c2,…,cn]T表示虚拟控制矢量,以确保跟踪位置误差z1可以收敛到一个以零为原点的邻域内。 考虑到物体位置x1的约束,并为了确保系统的稳定性,选择IBLF,其表达式为 (21) 引理2在{|x1i| (22) 对式(21)求导,可以得到 (23) 其中, 式中,ci为虚拟控制器,其表达式为 (24) 式中,pi表示正控制增益。 (25) 由于|xdi| 将式(24)代入式(23),得到 (26) 为确保系统稳定性,构造新的IBLF,其表达式为 (27) 对式(27)求导,可以得到 (28) (29) 将式(24)和式(29)代入式(28),并结合性质1和性质2,式(28)进一步可以表示为 (30) 其中, 根据引理1的万能逼近性,Ψ中的未知连续函数向量可以用模糊逻辑系统近似,则Ψ可以表示为 (31) 其中, κ=[κ1,κ2,…,κn]T ε=[ε1,ε2,…,εn]T Fo=O1×n (32) (33) (34) (35) 证明若滑模面选择为 (36) (37) 通过式(37)可以实现定理1,证毕。 当系统状态到达滑模面s=0时,意味着‖Z‖≤β|ρ|满足。在这种情况下,可以得到‖z2‖≤β|ρ|,于是将模糊自适应控制器和3个自适应律分别设计为 (38) (39) (40) (41) 其中, 式中,参数γ,μ2,τi,η2i,λi和δ2i是由用户给出的正常数。将式(31)和式(38)代入式(28),则可得 (42) 选择如下IBLF,其表达式为 (43) 对V3微分,可得 (44) 考虑到不等式 (45) (46) 将式(45)和式(46)代入式(44)中,得到 (47) (48) 为确保跟踪误差收敛到一个以零为原点的零域内,则对式(48)积分,表达式为 (49) 由此可以得出定理2。 定理2如果同时满足假设1和假设2,并在‖Z‖≤β|ρ|紧域上时,所设计的自适应律式(39)至式(41)和自适应控制器式(38),可以确保多机械臂携带同一物体时的跟踪误差收敛到一个以零为原点的邻域内。同时,保证闭环系统中的所有信号一致最终有界。 为了总结控制设计技术,控制方案的稳定性过程由定理3描述。 多机械臂系统包括两个机械臂、一个物体和两个机械臂末端执行器上的力传感器。 物体的期望轨迹选择为 式中,t为期望轨迹的时间。 物体动力学系统式(3)的参数为 式中:参数mo表示物体的重量;g表示重力加速度;mo=5 kg,g=9.8 m·s-2。 第i个机械臂的参数设置为 式中:Ni11=bi1+2bi2cos(ri2)+2bi3cos(ri3)+2bi4cos(ri2+ri3);Ni12=bi5+bi2cos(ri2)+2bi3cos(ri3)+bi4cos(ri2+ri3);Ni13=bi6+bi3cos(ri3)+bi4cos(ri2+ri3)Ni21=Ni12;Ni22=bi5+2bi3cos(ri3);Ni23=bi6+bi3cos(ri3);Ni31=Ni13; bi7cos(ri1)+bi8cos(ri1+ri2)+bi9cos(ri1+ri2+ri3);Hi2=bi8cos(ri1+ri2)+bi9cos(ri1+ri2+ri3);Hi3=bi9cos(ri1+ri2+ri3)。定义Ii=[bi1bi2bi3bi4bi5bi6bi7bi8bi9]T表示第i个机械臂的物理参数,参数设置为I1=I2=[4.81 1.29 0.05 0.05 1.30 0.12 3.62 1.29 0.05]T。 第i个机械臂末端执行器和关节的雅可比矩阵Γi(ri)的参数选择为 式中:Γi11(ri)=-li1sin(ri1)-li2sin(ri1+ri2)-li3sin(ri1+ri2+ri3);Γi12(ri)=-li2sin(ri1+ri2)-li3sin(ri1+ri2+ri3);Γi13(ri)=-li3sin(ri1+ri2+ri3);Γi21(ri)=li1cos(ri1)+li2cos(ri1+ri2)+li3cos(ri1+ri2+ri3);Γi22(ri)=li2cos(ri1+ri2)+li3cos(ri1+ri2+ri3);Γi23(ri)=li3cos(ri1+ri2+ri3);Γi31(ri)=Γi32(ri)=Γi33(ri)=1。参数li1、li2和li3分别表示第i个机械臂的连杆1、连杆2和连杆3的长度(i=1,2),其中l11=l21=2 m,l12=l22=1.5 m,l13=l23=0.5 m。 第i个机械臂末端执行器和被抓取物体的雅可比矩阵Ji(xo)选择为 式中,lio是第i个机械臂末端执行器到物体质量中心的长度,lio的实际值为l1o=l2o=0.5 m。 为补偿未知非线性函数Ψi,选择语言变量的域为 式中,r=1,2,…,18是第r个状态变量,标记负大(Negative Big,NB)、负中(Negative Middle,NM)、负小(Negative Small,NS)、负零(Negative Zero,NZ)、正零(Positive Zero,PZ)、正小(Positive Small,PS)、正中(Positive Middle,PM)和正大(Positive Big,PB)表示语言变量。 图2 位置跟踪轨迹的3种方法 图3 3种方法的跟踪误差 由图2和图3可以看出,模糊自适应控制的位置跟踪速度最快,逼近误差更小,并且位置跟踪误差可以收敛到以零为原点的邻域内。在未违反输出约束条件下物体沿着期望信号运动过程中,可以看出模糊自适应控制的跟踪轨迹与跟踪误差效果优于自适应控制与模糊PD控制。 为了说明模糊自适应控制中的自适应律较少,将模糊自适应控制中的自适应律与模糊PD控制中的自适应律进行比较,具体分别如图4和图5所示。 图4 模糊PD控制中的自适应律 图5 模糊自适应控制中的自适应律 由图4和图5中可以看出,模糊自适应控制相较于模糊PD控制而言,具有较少的自适应律,且能够提高计算效率。 为了更清楚地体现出模糊自适应控制具有精准的跟踪效果,对物体在笛卡尔空间中跟踪期望轨迹进行分析,具体如图6所示。由图6可以看出,在笛卡尔空间中,物体在跟踪理想轨迹xd运动时具有较好的跟踪效果。 图6 在笛卡尔空间中物体的运动轨迹 关于模糊自适应控制中的速度跟踪响应及跟踪误差的情况具体如图7和图8所示。由图7和图8可以看出,模糊自适应控制具有稳定的速度跟踪性能,并且跟踪误差能够收敛到以零为原点的邻域内。在多机械臂携带物体运动的过程中,通过系统施加在物体上控制扭矩的大小确保模糊自适应控制器Fo的有效性,具体如图9所示。由图9可以看出,系统施加于物体的控制扭矩是平滑且有界的,并能够在短时间内稳定到一个相对较小的范围中,因此所提的模糊自适应控制器Fo是有效的。 图7 模糊自适应控制中的速度跟踪响应 图8 跟踪误差 图9 系统施加于物体的控制扭矩 针对具有未知动力学和输出约束的多机械臂系统,设计了一种基于逼近精度和李普希兹系数的自适应模糊逻辑系统控制器。首先,通过对FLS系统的万能逼近原理引入了一个非零参数来逼近非线性函数。其次,利用IBLF的稳定性原理设计的控制器与自适应律保证了系统在FLS逼近域内时的稳定性,针对系统状态在FLS域外时的情况,通过滑模控制的方法将状态拉回到FLS域内。最后,将所设计的模糊自适应控制器与自适应控制器和模糊PD控制器进行仿真对比。仿真结果表明,与这两种控制器相比,所提出的控制器可以确保在不违反输出约束的情况下,具有良好的跟踪性能,同时能在线更新自适应律,并且闭环系统中的所有信号均满足一致最终有界。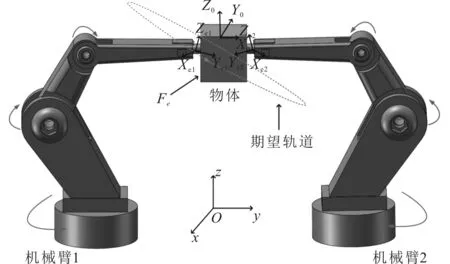

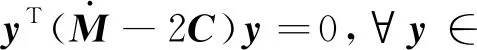

1.2 FLS系统
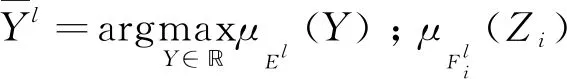
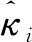

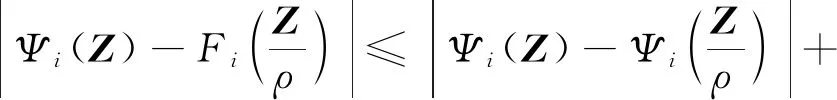
2 具有输出约束的控制器
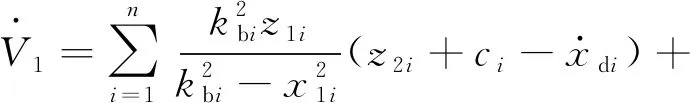
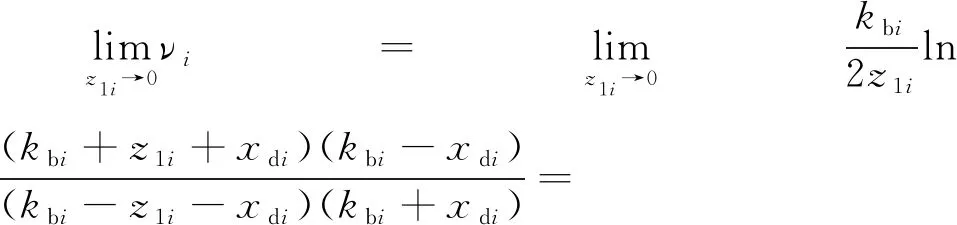
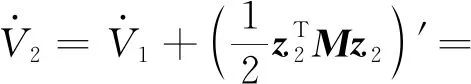
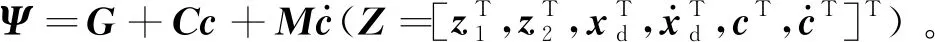
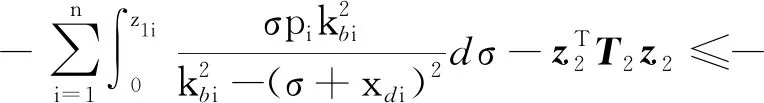
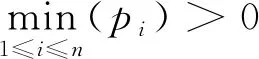
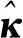
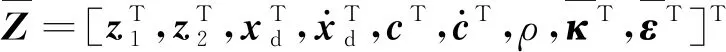
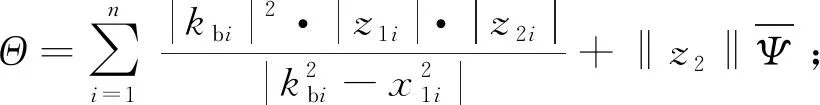
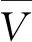

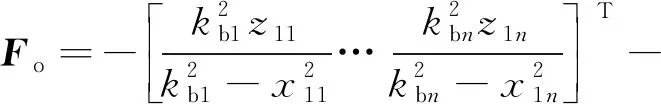

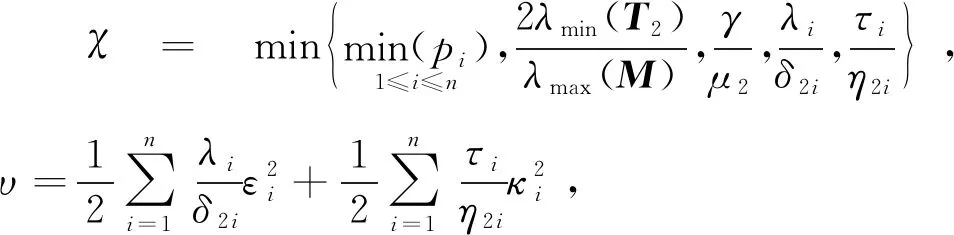
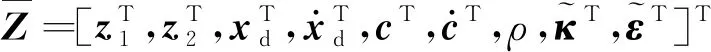
3 仿真结果及分析
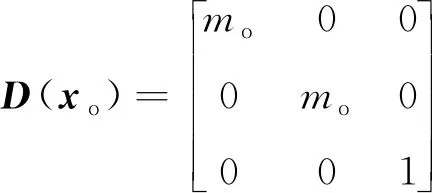
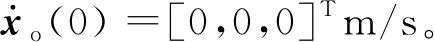

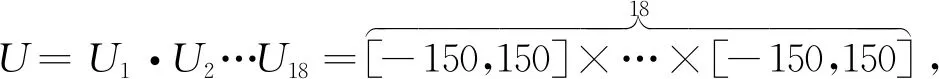
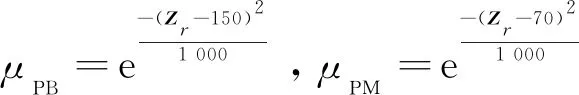
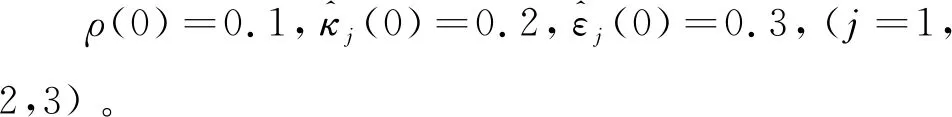




4 结语

