一种塔吊钢丝绳损伤检测信号降噪方法

杨春杰,李聪聪,刘满仓

(1.西安邮电大学 自动化学院,陕西 西安 710121;2.陕西昱琛航空设备股份有限公司 质量与售后中心,陕西 西安 710089)

塔吊钢丝绳安全事故在世界范围内屡见不鲜,为了有效防止钢丝绳断裂事故的发生,亟需研究有效的钢丝绳损伤检测方法。目前,钢丝绳损伤检测方法主要包括漏磁检测法、声学检测法、涡流法、辐射法和机械振动法。其中,漏磁检测方法具有不受油污干扰、便于使用等优点,在工程中应用更为广泛。为了扫描整个钢丝绳表面,研究人员经常使用磁传感器阵列收集多通道损伤信号,提供丰富的损伤诊断信息[1]。

钢丝绳损伤检测信号中的噪声来自钢丝绳本身的结构特性及其运行环境,主要包括钢丝绳的股波噪声、钢丝绳运行过程中的抖动以及检测环境周围复杂磁场等干扰[2]。同时,传感器也会受到环境温度变化等因素影响,加剧采集信号的“零漂移”现象,对检测信号造成强烈干扰[3]。因此,对采集的原始钢丝绳漏磁损伤信号进行降噪预处理尤为重要。

传统降噪方法是使用有限长单位冲激响应 (Finite Impulse Response,FIR) 滤波器或无限脉冲响应(Infinite Impulse Response,IIR) 滤波器滤除噪声,从而保留真实损伤信号。然而,传统滤波方法要求输入信号的频率范围已知,很难区分未知频率的干扰信号,降噪后也存在“Gibbs”现象[4]。钢丝绳漏磁检测信号是一种非平稳、非周期性的冲击信号[5],小波阈值降噪[6-7]可以有效地处理这种非平稳信号,实现损伤信息的提取、降噪,但小波变换需要一定的先验知识,降噪效果取决于小波基函数和分解层数的选择,并且只有针对已知噪声的频率范围且信号和噪声的频带相互分离时是有效的。经验模式分解法(Ensemble Mode Decomposition,EMD)不需要先验知识,具有很强的适应能力。文献[8]将EMD与排列熵或小波变换相结合,提取了钢丝绳断裂的信号特征,但在损伤信号中仍然存在“模态混合”和“端点效应”的问题。为此,Huang等[9]又提出集合经验分解(Ensemble Empirical Mode Decomposition,EEMD),虽然EEMD方法改善了模态混频问题,但该方法会使信号失真。考虑到EEMD在分解过程中没有消除增加的噪声,存在信号重建误差增加的问题,M.E.TORRES等[10]提出了自适应噪声完备集合经验模态分解(Complete Ensemble Empirical Mode Decomposition with Adaptive Noise,CEEMDAN)。基于CEEMDAN和最优小波的心音降噪方法[11]对心音信号降噪的效果明显。CEEMDAN结合小波阈值去噪[12]处理超声无损检测缺陷信号,相比于EEMD方法,提高了信噪比,降低了迭代次数。然而,小波阈值去噪方法更适用于处理噪声信号频率已知的缺陷,针对未知频率信号降噪处理,小波包阈值降噪(Wavelet Packet Threshold Denoising,WPTD)方法可以提供更细致的频率分解,更好地保留处理信号的频率特性。因此,为解决钢丝绳漏磁检测信号中存在的未知频率噪声干扰问题,拟提出一种基于多尺度样本熵(Multi-scale Sample Entropy,MSE)的CEEMDAN联合WPTD方法。先将钢丝绳漏磁检测信号通过CEEMDAN分解为多个本征模态函数(Intrinsic Mode Functions,IMF)分量,计算各IMF分量的多尺度排列熵区分含有未知频率噪声干扰的IMF分量。然后通过实验确定小波包阈值去噪的最优先验条件,对含有噪声的IMF分量进行降噪处理,从而达到噪声与有用信号的干净分离。

1 联合降噪方法

基于多尺度样本熵的CEEMDAN联合WPTD方法先利用CEEMDAN将检测信号分解得到多个固有模态分量,通过计算各固有模态分量的多尺度样本熵筛选出含有噪声的固有模态分量,然后通过小波包分析阈值降噪,将降噪的新模态分量与保留的模态分量重构得到干净的损伤信号。钢丝绳漏磁检测信号经过联合降噪方法处理过程如图1所示。

图1 联合降噪方法处理过程

1.1 检测信号分解

假设钢丝绳漏磁原始检测信号为x(t),则检测信号x(t)经过CEEMDAN处理具体步骤如下。

步骤1将添加的符合正态分布的高斯白噪声Ni正负成对的多次加入到x(t)中,经过EMD分解,得到第一阶模态分量

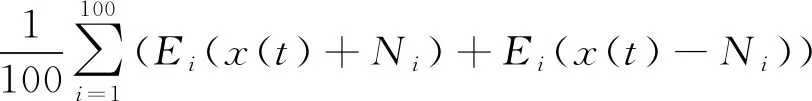
(1)

式中:i为添加噪声次数;Ei(•)为第i次加入高斯白噪声时的EMD分解。

步骤2分离第一阶态分量,计算剩余残差

r1(t)=x(t)-F1

(2)

步骤3将r1(t)作为新输入,重复步骤1,得到第二阶模态分量

(3)

步骤4分离第二阶模态分量,计算剩余残差

r2(t)=r1(t)-F2

(4)

步骤5重复上述步骤,直至获取的残差只有2个极值点(单调函数),不能继续分解,停止计算。假设共分解出k个IMF分量,则此时原始信号x(t)可以表示为

(5)

式中,Fm为第m个IMF分量。

1.2 各IMF分量的多尺度样本熵计算

样本熵确定单一尺度信号的复杂程度,但是,样本熵并没有考虑到时间序列信号中存在不同的时间尺度,为了计算不同尺度下信号的复杂性,将多尺度样本熵[13](Multi-scale Sample Entropy,MSE)引入其中。钢丝绳漏磁信号经过CEEMDAN分解得到多个IMF分量,计算各IMF分量的MSE,衡量各IMF分量的复杂度,进而区分含噪IMF分量和信号IMF分量,具体步骤如下。

步骤1对CEEMDAN分解得到的IMF分量进行粗粒化,以创建新序列。以IMF分量Fm(t)为例,通过计算τ个连续数据点的平均值形成粗粒化后的序列为

(6)

式中:N为数据长度;τ为时间尺度,值取正整数。当τ=1时,结果就是原始时间序列。

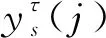
步骤3计算各IMF分量的多尺度样本熵,并进行归一化处理,多尺度样本熵可表示为

(7)

式中:p为嵌入维数;q为匹配阈值。

多尺度样本熵的阈值一般取0.6,熵值大于0.6即可认定为信噪混合分量[14],将熵值大于0.6的分量进行降噪处理,熵值小于0.6的分量保留。

1.3 小波包阈值降噪

WPTD是在小波变换的基础上提出来的,小波包分析能够处理小波降噪过程中忽略的高频分量,可以进一步处理高频噪声分量。假设原始钢丝绳漏磁信号经CEEMDAN得到的多个IMF分量,经过计算各分量的多尺度样本熵并分析出含噪IMF分量和干净IMF分量,则对含噪IMF分量进行降噪的具体步骤如下。

步骤1确定小波包阈值降噪的先验知识。如分解层数、小波基函数的选取、阈值函数以及阈值判断方法。

步骤2对被处理的含噪IMF分量进行多层小波包分解。

步骤3针对每个含噪IMF分量分解的小波包系数选取合适的阈值进行阈值量化。

步骤4通过小波包重构还原IMF分量。

在进行小波包分析时,需选择一个合适的阈值和阈值函数。如果阈值设置太大则造成有用信号的损失,设置太小噪声则没有被完全的清除,过滤效果较差。

2 实验及结果分析

钢丝绳漏磁检测基于电磁感应[15],利用磁化体励磁钢丝绳产生磁场。当励磁后的钢丝绳经过检测终端时,终端中感应线圈产生感应电动势。如果钢丝绳发生断裂损伤,则感应线圈感应的电动势将发生变化,感应电动势变化的大小则反映钢丝绳的损伤程度。为了验证联合降噪方法的有效性,搜集了几根不同直径和断丝根数的钢丝绳作为检测对象,损伤情况如表1所示。

表1 不同类型钢丝绳损伤情况

实验分别采用直径为14 mm、16 mm和20 mm的钢丝绳,并制造 6根,9根和12根断丝损伤。设置原始信号点数N=2 000,采样频率fs=200,采样时间为T=10 s,原始钢丝绳漏磁信号经CEEMDAN分解得到的11个IMF分量(IMF1～IMF11)和1个剩余残差r11如图2所示。

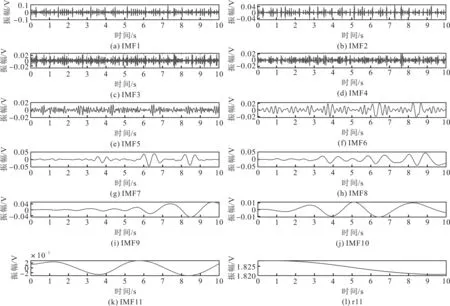
图2 IMF分量及剩余残差波形

计算每个IMF分量的多尺度样本熵EMSE,并进行归一化处理,结果如表2所示。

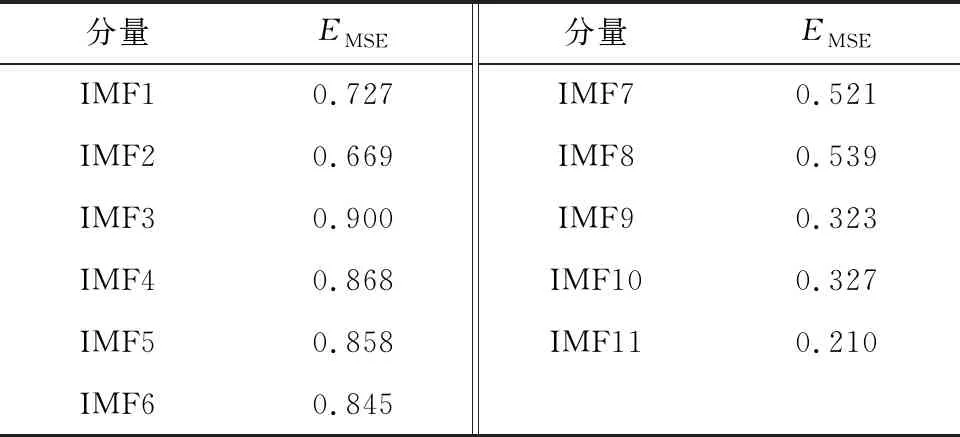
表2 各IMF分量的多尺度样本熵均值

熵值越大,信号复杂度越高。从表2可以看出,通过CEEMDAN分解得到固有模态分量的前6层IMF分量的多尺度样本熵的均值大于0.6,说明前6层IMF分量包含噪声信息。

各IMF分量幅频如图3所示。前5层IMF分量主要频率均大于10 Hz,由于钢丝绳漏磁信号传感器检测的钢丝绳损伤信号频率范围在3 Hz～7 Hz,因此对图3幅频分析可知,IMF1～IMF5分量确实存在噪声干扰,IMF6分量可能包含少部分噪声信息。

图3 各IMF分量幅频

为了分析不同小波基函数和阈值函数对检测信号降噪效果的影响,以信噪比(Signal-to-Noise Ratio,SNR)和均方根误差(Root Mean Squared Error,RMSE)作为降噪评价指标,选取daubechies小波系列(db小波)、symlets小波系列(sym小波)、colief小波系列(coif小波)和biorN.N小波系列作为备选小波基函数,对上述采集到的10 s钢丝绳损伤检测检测信号进行分析,不同小波基函数降噪结果如表3所示。在对信号进行降噪过程中,将小波分解层数设置为6层。

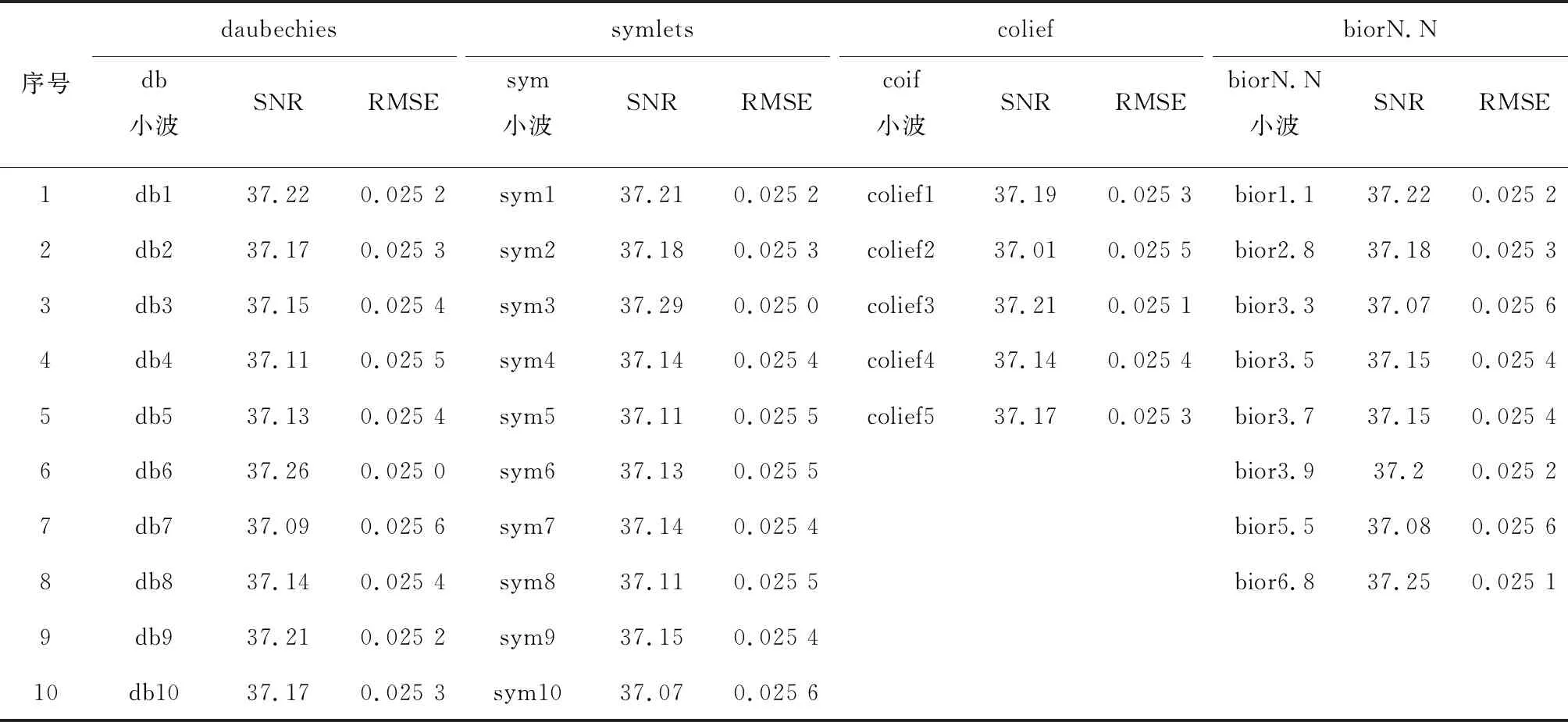
表3 不同小波基函数的降噪结果

从表3可以看出,db6小波、sym3小波、coif3小波和bior6.8小波分别在各自系列小波函数中降噪性能最好。因此,初步选取此4种小波基函数对钢丝绳损伤检测信号进行降噪。

在降噪的过程中,为确定钢丝绳漏磁检测信号降噪的最佳分解层数,将db6、sym3、coif3和bior6.8小波函数将钢丝绳损伤检测信号分解为1～10层,不同分解层的降噪结果如表4所示。

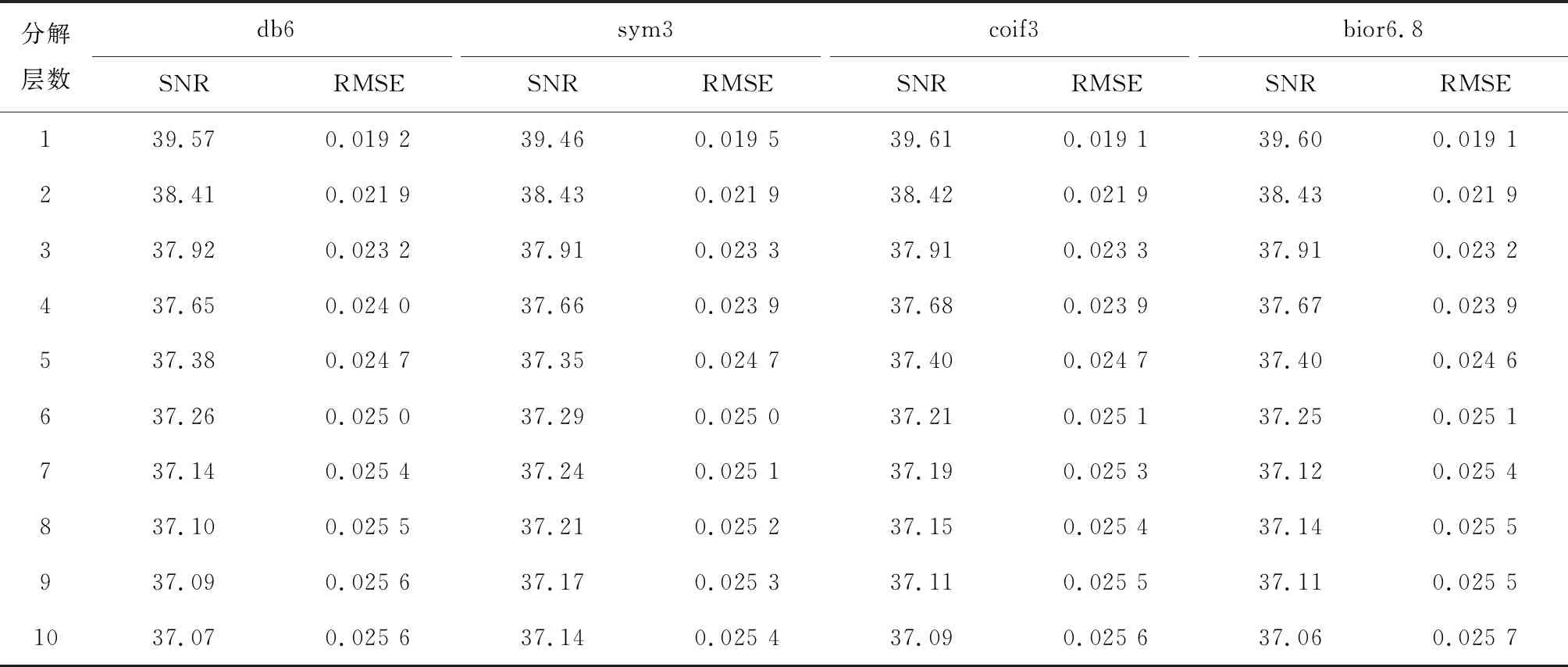
表4 不同分解层数检测信号的降噪结果

从表4可以看出,除随分解层数的变化速率外,降噪评价指数随分解层数的递增趋势一致。

为确定最佳分解层数,采用均方根误差量和信噪比作为降噪效果的评价指标,均方根误差变化量和信噪比变化量随分解层数的变化对比结果如图4所示。从图4可以看出,均方根误差变化量和信噪比变化量均在第8个值之后趋于稳定。因此,钢丝绳损伤信号的最佳分解层数为8层或9层,为了减少检测信号降噪过程中的计算量,选取8层进行分解。

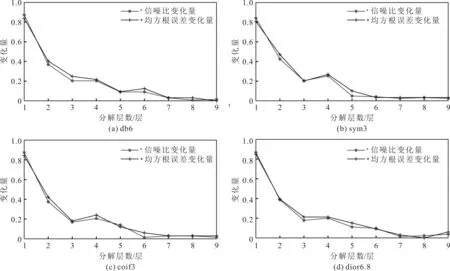
图4 均方根误差变化量和信噪比变化量随分解层数的变化对比结果

根据上述选取的小波基函数和分解层数分别选取启发式阈值法(heursure)、无偏似然估计法(rigrsure)、固定阈值法(sqtwolog)和极大极小原理阈值法(minimaxi) 等常用的4种阈值规则对损伤检测信号进行硬(hard)、软(soft)阈值[6]降噪,结果如表5所示。

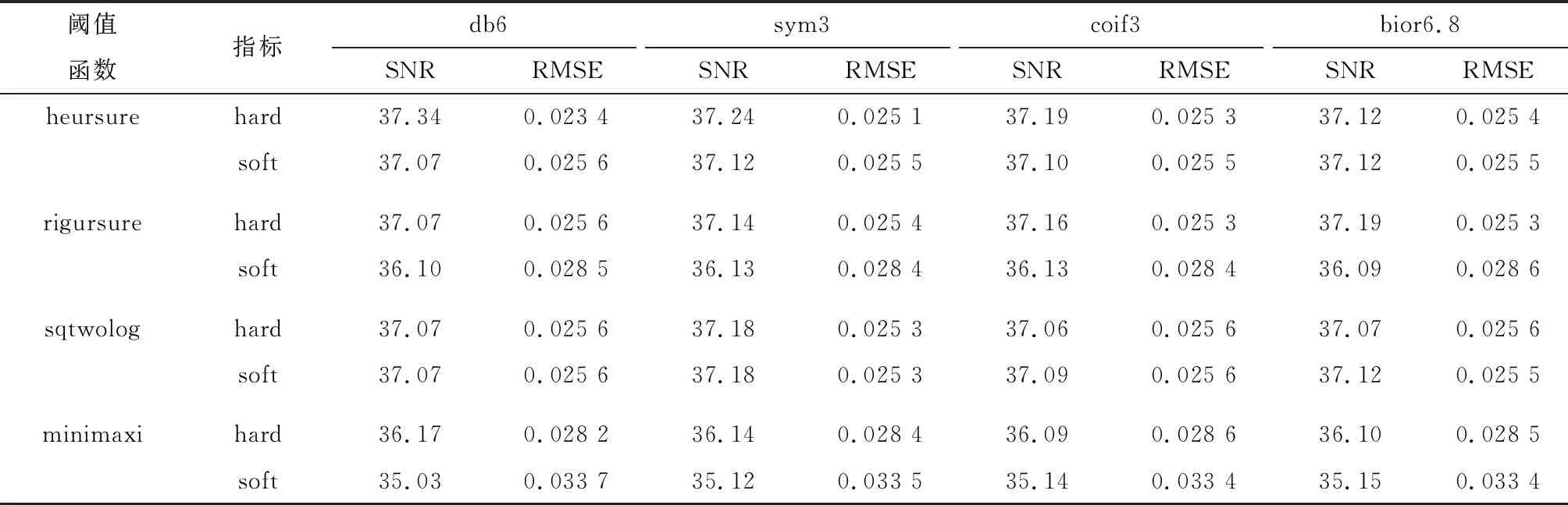
表5 4种阈值规则下的降噪结果

由表5可知,选择heursure阈值规则下的硬阈值处理去噪效果最好。综合表3至表5结果,设置db 6小波函数,8层小波包分解,heursure阈值规则下的硬阈值处理,恢复信号降噪效果最好。

为评价该方法降噪效果,将联合降噪方法与WPTD、变分模态分解(Variational Mode Decomposition,VMD)、CEEMDAN和EMD-MSE-WPTD等5种方法进行对比,结果如图5所示。从图5可以看出,WPTD处理后的信号仍含有大量的噪声,VMD方法对信号尾部进行了扭曲,CEEMDAN方法和EMD-MSE-WPTD方法处理的结果均没有该联合降噪方法平滑。

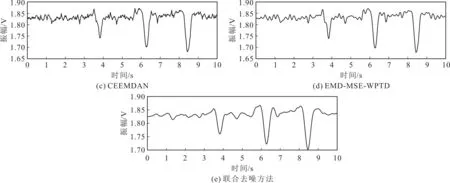
(续)图5 5种降噪方法降噪结果

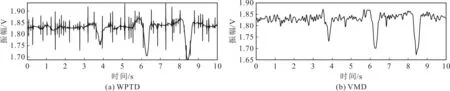
图5 5种降噪方法降噪结果

降噪后的信号频谱分析如图6所示。可以看出,所提联合降噪方法对钢丝绳损伤信号的降噪效果更显著,将有用信号保留在10 Hz以内,得到的信号更加平滑,无杂波混叠,更有利于特征提取,在保持局部波形特征和峰值不变的情况下,基本消除了噪声分量,而其他4种方法的频谱图显示降噪后信号在大于10 Hz频率信号中仍含有噪声,噪声与有用信号难以有效分离,干扰了钢丝绳损伤检测信号。

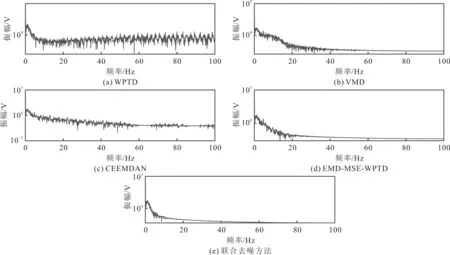
图6 5种方法降噪信号的频谱

将信号降噪后的SNR、RMSE、平滑度r和余弦相似度c作为降噪评价指标分析5种方法的降噪效果,对比结果如表6所示。

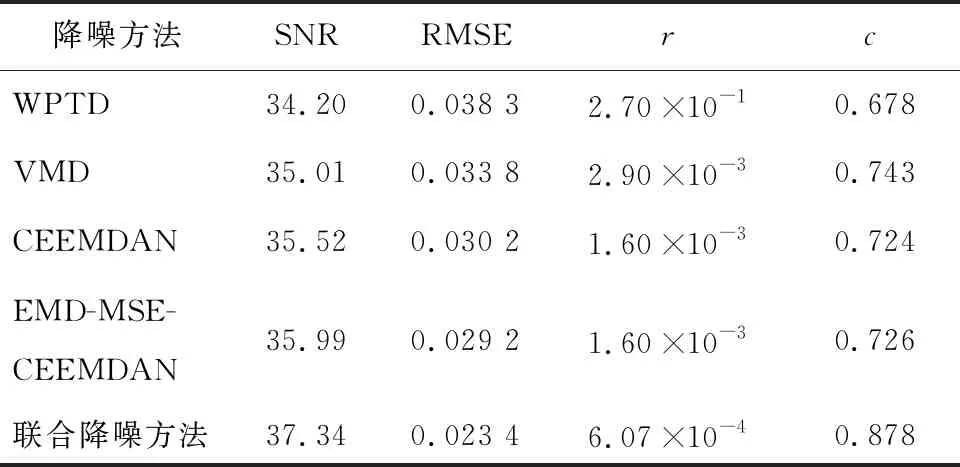
表6 5种方法的降噪评价指标对比

由表6可以得出,联合降噪方法的SNR(37.34 db)最大,RMSE(0.023 4)最小,信号平滑度最小(6.07×10-4),余弦相似度最大(0.878),降噪效果最好。与小波包阈值降噪方法相比,SNR提高了3.14 dB,RMSE降低了0.014 9。与VMD降噪方法相比,SNR提高了2.33 dB,RMSE降低了0.010 4。与CEEMDAN降噪方法相比,SNR提高了1.82 dB,RMSE降低了0.006 8。与EMD-MSE-WPTD降噪方法相比,SNR提高了1.35 dB,RMSE降低了0.005 8。该联合降噪方法计算的信号平滑度也明显小于其他4种降噪方法。在余弦相似度方面,联合降噪方法计算出的c值最大,说明该方法得到的降噪信号与原始信号最接近,处理效果最佳。

3 结语

基于多尺度样本熵的CEEMDAN联合WPTD降噪方法处理钢丝绳损伤检测信号,能够有效地区分出纯净分量和含噪分量,利用WPTD对含噪分量进行处理,得到降噪后的分量,将其与保留的纯净分量进行重组得到降噪后的检测信号,解决了检测信号中含有未知频率噪声干扰的问题。实验结果表明,当小波基函数为db6,分解层数为8时,heursure准则下的硬阈值最适合用于钢丝绳损伤检测信号的降噪预处理。将该方法降噪结果分别与WPTD、VMD、CEEMDAN和EMD-MSE-WPTD等方法进行比较,经过联合降噪方法的信噪比最大,均方根误差最小,处理后的钢丝绳损伤检测信号更加平滑,检测信号的损伤特性得到很好的保留。因此,该联合降噪方法具有更好的降噪效果,并验证了联合降噪方法在钢丝绳损伤信号降噪预处理中的可行性。