素养立意 结构化选材——以人教版教材三年级上册“多位数乘一位数”单元复习为例

□徐 佳

单元复习课中选择的学习材料容易局限于单元内知识的整理，缺少知识应用的情境，缺少核心概念的引领，使单元复习教学变得琐碎零散，难以满足不同层次学生的学习需求。计算相关单元的复习该怎么选取学习材料？怎样的学习材料有助于组建核心任务，助推学生的学习进阶？笔者基于结构化选材的视角，对人教版教材三年级上册“多位数乘一位数”单元复习进行了以下尝试。

一、以运算本质引领核心内容

单元复习教学要在核心素养的统领下提炼单元核心内容，利用任务驱动筛选学习材料。因此，教师要明确复习内容的领域和主题特色，整体解读教材编排结构。

首先，聚焦素养分析主题特色。“多位数乘一位数”单元属于“数与运算”主题，发展数感、提升运算能力是本单元学习材料设置的出发点。进一步分析单元关键要素，人教版教材按两位数乘一位数、多位数乘一位数，再到三位数乘两位数的顺序编排，其本质核心是运算律的应用。学生在学习两位数乘一位数时，就已经接触了分拆计算再合并相加的长算式，从而由口算过渡到笔算，逐步感悟分别相乘再相加的过程。在此基础上向后延伸，迁移“分—算—合”的过程，就是应用运算律的过程。算理前后一致，算法前后延伸。可以说，多位数乘一位数是整数乘法承前启后的节点。

其次，梳理教学内容分析单元基本内容。“多位数乘一位数”单元的教学内容包括口算乘法、笔算乘法和应用乘法解决问题三个部分，共11个例题。其中，解决问题中还设置了用估算解决问题、归一问题和归总问题三类问题。解决问题是乘法计算的应用，其中数量关系的分析是本单元的教学重点之一。

由此明确复习的核心内容应聚焦笔算，联系口算、估算和简算等不同的计算形式；关联归一问题和归总问题的数量关系，建立数学模型。同时明确正确运算、理解算理、灵活选择合适的计算方法，培养学生读图析题的能力是本单元复习的综合目标；发展数感，提升运算能力是计算复习的终极目标。

二、以实证分析确立核心任务

素养立意的学习材料要基于学情选取，以实现单元复习教学查漏补缺的功能。因此，教师要基于实证分析来了解学情，把握学生学习中的易错点和差异点，确立核心任务。

（一）易错点——连续进位的乘法

单元复习教学前，教师根据笔算乘法中的不同题型设置了前置式任务：189×6、309×6、514×4、890×7、668×9。测试结果显示，对于笔算乘法中的连续进位情况，学生运算的准确率较低。而在连续进位乘法中，笔算189×6 的正确率比笔算668×9 的正确率高。可见，因数较大的计算更容易出现错误，即使是像890×7 这种其中一个因数末尾有0 可以转化为两位数乘一位数的乘法，一旦因数数据大且连续进位，学生的错误率就会很高。因此，在计算教学中夯实基础、操练技能仍然是复习课的关注点。

（二）差异点——主动优化算法

前置式任务中的解决问题是：陈伯伯家一共摘了180千克苹果，1个箱子最多可以装6千克苹果，32 个箱子能装下这些苹果吗？测试结果显示，只有约13%的学生能主动利用估算解决问题，其余学生都是用笔算解决问题的。由此可见，学生认为笔算是保证计算准确性的最优选择，缺少灵活选择算法的意识。为此，教师在教学中要提供情境性的学习材料，以多层次的问题驱动，促使学生灵活选择计算方式，在对比中感受使用不同计算方式的优势，在计算方式的选择中提升运算能力。

三、以结构化材料驱动任务

单元复习教学要利用结构化学习材料，推动学生主动学习，促进学生对知识本质的理解，使学生随着学习任务的不断递进和学习内容的不断扩展，不断完善知识结构的建构。

（一）情境性材料，再现计算方法

以问题情境驱动任务，可以使学生在学习进阶中完成计算方法的自主选择，实现对笔算方法的再现回顾。因此，教师在“多位数乘一位数”的单元复习中，创设了基于8张数卡的主题情境（如图1）。

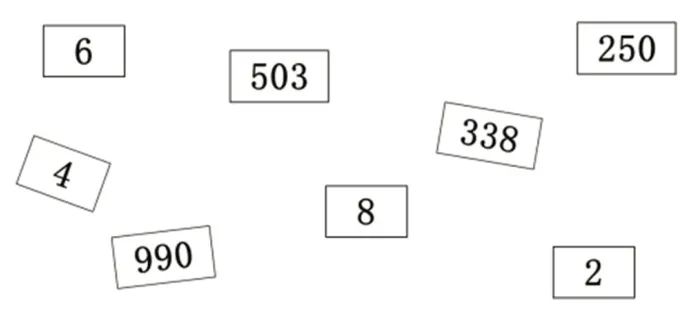
图1

任务一：找出相乘的积接近2000 的两个数。

在问题“哪两个数相乘的积接近2000”的驱动下，学生可能会猜想的算式是：①250×8；②338×6；③503×4；④990×2。教师提问：“你们是怎么想到这些算式的？”结合学生的回答，引导他们复习口算和估算的计算方法。其中，算式503×4、990×2、338×6既可以用四舍五入法进行估算，也可以采用首位估算的方法。由此，学生感受到估算的基础是口算，这些方法方便快捷。

递进任务1：在积接近2000 的三道算式（503×4、990×2、338×6）中，哪道算式的积最接近2000？学生发现用估算和口算不能解决问题，从而产生了用笔算的需求，从中进一步感悟到笔算的精确性。这三道笔算乘法分别涉及因数中间有0、因数末尾有0以及连续进位等情况，学生可借助不同类型的笔算乘法，复习多位数乘一位数的计算方法。

递进任务2：教师呈现前置式任务中学生出现的错误（如图2），让学生思考“可以用什么方法来判断计算结果是错误的”，引导学生用乘数末位相乘的方法判断②号竖式和③号竖式的计算结果是错误的，通过计算发现①号竖式是连续进位造成的错误。在此基础上，让学生改正错误，说明计算过程中需要注意的地方。

图2

判断下列题目是否正确，并对不正确的进行修改。

在整体性的任务情境中，教师结合口算、估算和笔算的方法，引导学生回顾运算中的算理和算法，展现了学生自主选择的过程。同时引导学生运用相关知识进行合理的估算、判断和解释，发展了学生的数感和运算能力。

（二）关联性材料，理解运算本质

在教学中设计整体性的学习材料，有助于学生构建对后续学习有支撑意义和迁移应用价值的认知结构。计算复习教学的核心任务是计算方法的关联、迁移，但学生的迁移学习是有条件的，需要教师引导学生发现笔算乘法之间的共同特征，寻找它们之间的联系，感悟运算本质。

教师可以任务二为问题驱动，让学生在自主整理的过程中感受运算本质的一致性（如图3）。教师可以让学生自己举例，也可以借助前面任务一的多位数乘一位数算式，引导学生回顾多位数乘一位数的计算方法。如890×7，如果把890 看成89 个十，那么三位数乘一位数就变成了两位数乘一位数，通过比较两种计算方法，总结得到“都是从个位算起，用一位数依次乘多位数的每一位，哪一位上乘得的积满几十，就向前一位进几”。在此基础上，教师提问：大家猜一猜，以后还会学习怎样的乘法？学生猜测会学习四位数乘一位数、五位数乘一位数等内容。教师告诉学生以后不再继续学习多位数乘一位数，学生讨论其原因后感悟算法的共性，发现都是先拆分，再用一位数依次乘多位数的每一位，最后把每一位上的积合并相加，最终概括得出“分—算—合”的算法共性，为后续学习两位数乘两位数的计算方法做好铺垫。

图3

任务二：想一想、填一填，找一找关系。

通过关联性学习材料，将学习内容从两位数、三位数乘一位数，拓展到多位数乘一位数，总结出多位数乘一位数的计算法则，实现计算方法的关联，理解运算的本质。

（三）多元化材料，实现综合应用

针对不同学生的差异点，教师可以创设真实情境，借助多元结构化的学习材料，用问题解决的方式推进学生学习，丰富计算复习的教学内容。

1.图式性材料，辨析关系解释模型

教师可以让学生在图式的演示和辨析（如图4）中，理解归一问题和归总问题的数量关系，培养学生的几何直观和模型意识。

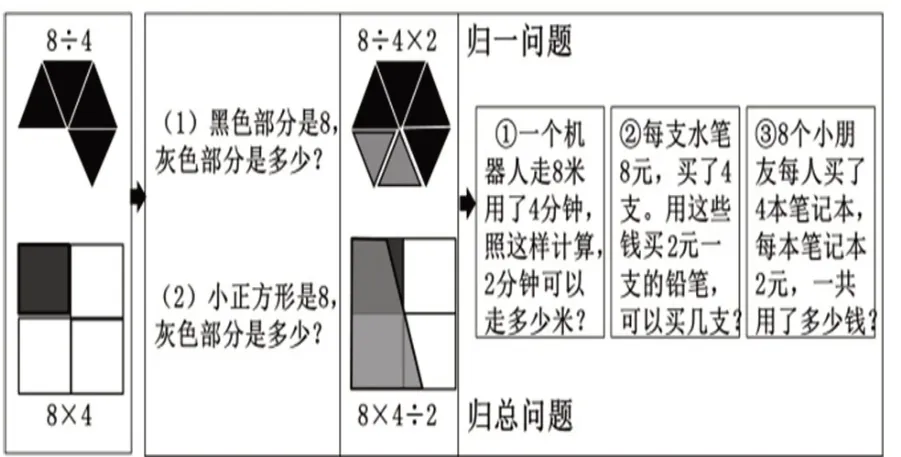
图4

任务三：根据图想算式，根据算式找题目。

第一层分析数量关系。针对图4，教师提问：想一想，如果4个三角形表示的是8，那么1个三角形是多少？如果1 个小正方形表示8，那么8×4 又表示什么？引导学生辨析8÷4 和8×4，理解平均分可得到“单一量”，以及几个几相加可求得总数。教师进一步提问：如果黑色部分是8，那么灰色部分是多少？如果小正方形是8，那么灰色部分是多少？引导学生思考：8÷4×2和8×4÷2这两个算式分别先求什么？让学生结合图式、文字、算式进行解释：8÷4×2先求1个三角形表示多少，再求2个三角形是多少；8×4÷2 先求总量表示多少，再算总量的一半是多少。由此，帮助学生理解归一问题、归总问题的数量关系。

第二层解释应用模型。教师让学生通过想一想、连一连、说一说，在图4的右边找出与8÷4×2和8×4÷2 对应的问题。引导学生分析题目：为什么题①用8÷4×2，题②用8×4÷2，题③用8×4×2？题①是有关行程的情境，速度是不变量，先用8÷4 求出速度；题②和题③都是购物的情境，其中题②的总价是不变量，先用8×4求出总价。通过几道题目的比较、辨析，学生初步理解了归一问题和归总问题的数学模型。

2.体验性材料，实际应用发展数感

教师可以让学生根据情境中的问题，灵活选择合适的方法解决实际问题，体会算用结合，增强学生综合解决问题的能力，发展数感（如图5）。

图5

解决问题（1）需要将问题转化为：分析行驶4分钟后的路程与1000米之间的关系，计算268×4的积时可以精算也可以估算。解决问题（2）则只需要估一估问题（1）的结果与2000 的关系。这两个问题都涉及多位数乘一位数的计算，问题解决的过程涵盖位置方位和对数大小的感知，以及灵活选择算法解决问题的能力。

核心素养立意下的计算单元复习教学，须凸显主题内容，以结构化学习材料为载体，利用多维度学习路径助推算法的选择，提升学生的知识技能。要让学生在联系中理解运算本质，构建认知结构；在综合应用中发展数学思维，提升运算能力，发展数感。