尼尔森体系系杆拱桥索力测试影响因素分析

秦 宁，李晶晶

（1.山东滕建建设集团有限公司，山东 枣庄 277500；2.滕州市智星电力电子工程有限公司，山东 枣庄 277500）

0 引言

近年来，随着高速铁路的快速发展，越来越多的系杆拱桥出现在铁路建设中。尼尔森体系系杆拱桥作为系杆拱桥的一种特殊形式，它是将斜吊杆代替普通系杆拱桥中的竖吊杆，大幅提高了结构的整体刚度，更好地满足桥梁在列车高速冲击下的动力要求。尼尔森体系系杆拱桥内部是一种超静定结构，任何一根吊杆索力发生变化都会影响整个吊杆系统的内力重分布，近而影响整个桥梁的安全性能［1］。因此，吊杆作为拱肋与系梁的传力构件及关键部分，对其索力的精确测试具有重要意义。目前，索力的测试方法主要有压力表对数法、压力传感器法、振动频率法、磁通量法等，各方法优缺点不一，测试误差不同，而在实际工程中，多选取振动频率法作为吊杆的主要测试方法。

1 振动频率法原理

振动频率法的工作原理是通过固定在吊杆上的加速度传感器，索力动测仪自动采集吊杆在受到拉力作用下的振动加速度信号，经分析后由频谱图确定吊杆的自振频率，然后根据吊杆的自振频率与吊杆索力之间的特定关系来确定吊杆索力［2］。

根据结构动力学原理［3］建立吊杆在轴向拉力作用下的自由振动方程见式（1）。

式中：m为吊杆的单位长度质量；u（x，t）为吊杆的横向位移；N为作用在吊杆两端不随时间变化的轴向拉力；为沿吊杆长度方向变化的抗弯刚度。

由式（1）可得吊杆两端铰接状态下的自振频率见式（2）。

振动频率法是基于弦振动理论推导出的索力测试方法，因此测试过程中必须满足以下假设：①吊杆两端边界条件看作铰接；②不受阻尼的影响；③不考虑垂度的影响。

但在索力实际测试过程中以上假设条件并不能完全满足，因此本文通过对以上影响因素分析，提出相应的解决办法以减少测量误差，使吊杆索力更符合设计要求。

2 工程概况

本文以某系杆拱桥为工程实例，该桥系梁全长148 m，计算跨度 144 m，梁端采用实心矩形截面，普通段采用单箱三室截面；拱肋立面投影矢高 28.52 m，矢跨比 1/5，拱肋采用二次抛物线并在横桥向内倾 8°呈提篮式，拱肋截面为哑铃型钢管混凝土等截面，上、下钢管及腹腔均为钢-混组合结构，拱内灌注 C55 自密实补偿收缩混凝土；两拱肋在拱顶处设1道一字撑，在拱顶至拱脚间设 6 道K型横撑；全桥共设 32 对吊杆，采用尼尔森体系布置；设计速度为 350 km/h，全桥立面图如图1 所示。

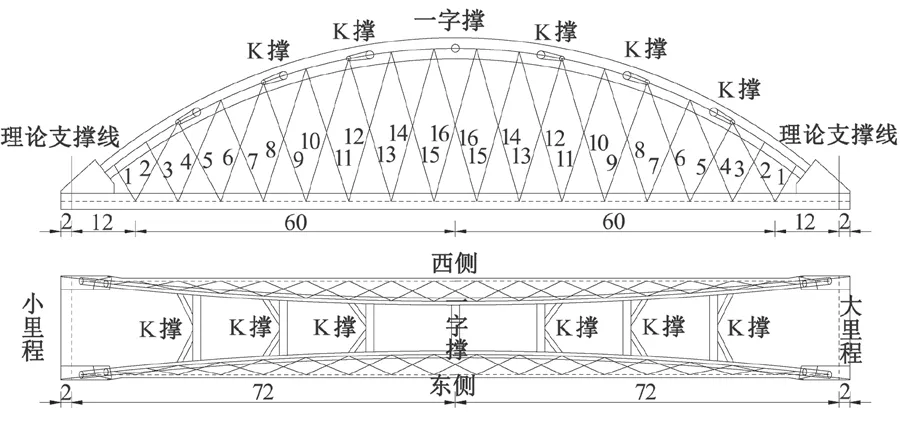
图1 全桥布置图（单位：m）

3 影响因素分析

3.1 边界条件的影响

吊杆在实际锚固过程中常采用螺母固结，由于每根吊杆索力大小不同，吊杆边界条件会偏向于铰接或固接［4］，因此在运用振动频率法测试索力时，并不能够完全满足上述假设条件。文献［5］指出，通过理论修正吊杆长度来消除锚头约束的影响，但文章并没有得出一个计算索力有效长度的解析式。结合工程情况，本文运用曲线拟合的方法得到吊杆有效长度的理论计算公式，并通过对比分析检验该公式的准确性。

吊杆在初张拉过程中，千斤顶张拉到设计值后在油泵不卸压的情况下测量每根吊杆的 1～6 阶频率，限于篇幅，现列出西侧小里程奇数号吊杆频率实测值如表1 所示。

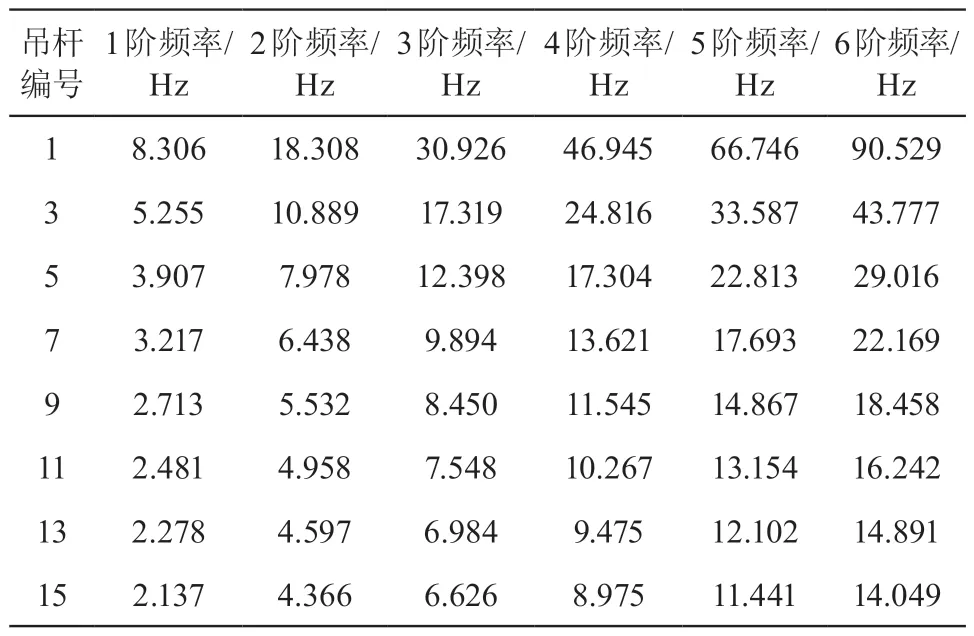
表1 吊杆频率实测值

由表1 分析可知，各阶频率之间并不成倍数关系，即频率从低阶到高阶依次呈增长的关系，这主要是由吊杆抗弯刚度的影响所致。因此，在该桥的索力测试过程中必须考虑吊杆抗弯刚度的影响，提高测试结果的精度。

在已知吊杆初张拉力、单位长度质量、抗弯刚度及各阶频率值的情况下，根据公式（4）分别计算每根吊杆在 1～6 阶频率下的长度L（1），L（2），…，L（6），将每根吊杆在 1～6 阶频率下的长度取平均值，即L1，L2，…，L6。运用软件 ORIGIN 将每根吊杆长度平均值进行公式拟合，根据拟合结果，可得吊杆的有效长度拟合公式见式（5）。

式中：l为吊杆有效长度，L为吊杆两锚固点间长度。

将西侧小里程奇数号吊杆两锚固点间长度代入公式（5）算出吊杆的有效长度，结合吊杆 1 阶频率分别计算各吊杆索力，并将计算结果与初张拉设计值对比，对比结果如表2 所示。

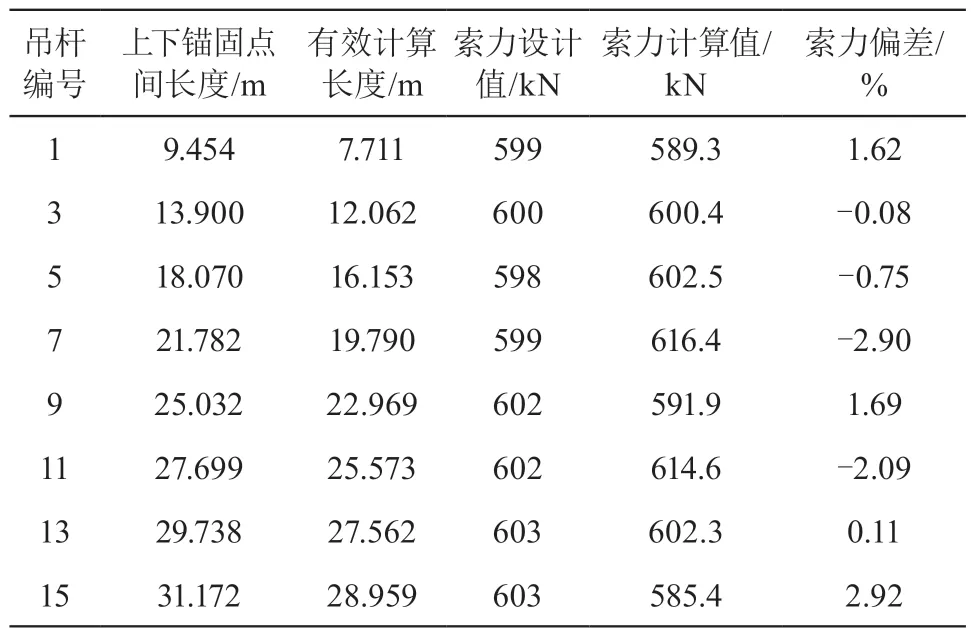
表2 吊杆索力设计值与有效长度计算值对比

由表2 分析可知，由于吊杆边界条件的影响，吊杆实际有效长度相对于上下锚固点间长度较短，通过有效长度算出的吊杆索力值与初张拉设计值偏差均在±3 %以内，说明通过拟合公式计算的有效长度可以等效替代基于弦振动理论所假设的边界条件，验证了吊杆有效长度的正确性。

3.2 减振器的影响

在吊杆初张拉完成后，为预防吊杆因振动幅度过大产生疲劳破坏，一般会在预埋钢管口处安装吊杆减振器［4］，安装位置如图2 所示。减振器的安装会对吊杆的频率产生影响，特别在吊杆二次调索阶段，对确定吊杆有效长度难度较大。文献［6］指出，阻尼器的影响可通过修正吊杆长度取其L-d（d=d上+d下）来消除，但其在理论推导该长度的过程中默认吊杆两锚固端是铰接状态，而在弦振动理论中两铰接点之间的实际长度并不等于L，因此在该理论的基础上提出了新的吊杆长度修正公式见式（6）。

图2 吊杆构造示意图

式中：Lj为考虑减振器影响的吊杆等效长度；d为锚固点到减振器中心位置的长度之和。

由于在初张拉完成后吊杆索力已重新分布，在安装了减震器的情况下无法确定吊杆索力实际值。结合ANSYS 有限元软件，建立长度修正后的吊杆有限元模型模拟实际情况，其中吊杆采用 LINK10 单元进行模拟并提取在初张拉力作用下的基频，同时将修正后的长度代入公式（3），按初张拉力大小计算基频。限于篇幅，现列出西侧小里程奇数号吊杆的两种基频计算结果如表3 所示。

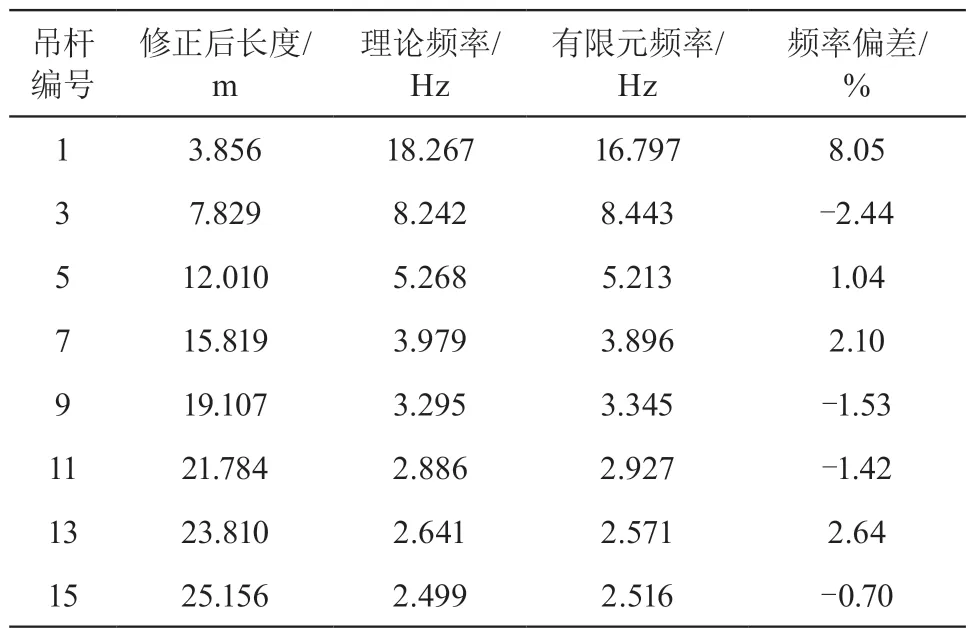
表3 理论计算频率与有限元计算频率对比

由表3 分析可知，1 号吊杆频率偏差达到 8.05 %，这因为当吊杆有效长度＜5 m 时，吊杆实际的振动不再符合弦振动理论，理论频率与实测频率相差较大［7］。对于有效长度＞5 m 的吊杆，通过两种方式计算出的频率偏差均在 ±3 % 以内，验证了该长度修正公式的正确性。

3.3 垂度的影响

关于吊杆垂度对索力的影响，文献［8］引入无量纲参数K，见式（7）。

式中：H为索力水平分量，lc为吊杆水平投影长度，A为吊杆截面面积，E为吊杆的弹性模量。

文献［9］分析了吊杆的振动频率f随参数K的变化规律，由结果可知，若使垂度对基频的影响控制在 5 % 以内，则相应的K值必须＞2.5。同时，吊杆垂度对 4 阶及以上频率的影响较小，即使K值小至 0.5，其影响也不超过 5 %。本文通过对系杆拱桥在初张拉力作用下进行K值计算，分析垂度对基频影响的大小。限于篇幅，现列出西侧小里程吊杆K值计算结果如图3 所示。

图3 吊杆 K 值变化图

由图3 可知，各吊杆的参数K值均＞24，由此得出该系杆拱桥吊杆垂度对基频影响很小，在满足工程允许误差范围内可对吊杆垂度忽略不计。同时，在吊杆有效长度拟合公式求解过程中，可以考虑仅使用 4～6 阶频率去计算，以此得到的结果更加精确。

4 结论

通过对吊杆影响因素的分析，得出以下结论。

1）在考虑边界条件的影响过程中，利用千斤顶张拉法测得吊杆的 1～6 阶频率，通过实测频率分析出吊杆弯曲刚度对频率的影响不能忽略，同时根据计算结果对吊杆有效长度进行公式拟合，对比分析运用拟合公式计算的吊杆索力与初张拉设计值偏差在 ±3 % 以内，验证了拟合公式的可靠性。

2）在考虑减振器的影响过程中，在原有吊杆长度修正公式的基础上提出新的吊杆长度修正公式，由于缺少实测数据检验，利用 ANSYS 有限元软件建立吊杆实际结构模型，通过对两种基频结果的分析得出在吊杆有效长度＞5 m 时，两种基频偏差均在 ±3 % 以内，验证了吊杆新长度修正公式的正确性。

3）在考虑垂度的影响过程中，通过分析吊杆的振动频率f随参数k的关系确定垂度对频率影响的大小，通过计算，每根吊杆的参数K值均＞24，得出垂度对吊杆频率影响很小，可以忽略不计。同时，建议在有效长度公式拟合时采用 4～6 阶频率，进一步提高结果的精度。Q