基于后验信息的压缩感知图像重构方法

李德高　程涛　许聪　王应山

摘 要：单像素相机的测量数据可采用正交匹配追踪（orthogonal matching pursuit，OMP）算法重构，但是重构得到的图像质量不好。本文提出一种提高图像重构效果的方法，该方法利用先验信息（列模平均值）判断重构效果优劣；通过测量数据相邻列相减的操作，以增强稀疏度。首先，基于OMP对测量数据逐列重构；然后，对重构效果差的列，作相邻列相减的操作后逐列重构；最后，通过逐列累加操作得到重构效果更好的图像。实验结果表明，该方法在仅使用OMP的情况下可以使重构图像的信噪比（signal to noise ratio，SNR）得到很大提高，虽然重构图像上有很明显的条纹，但是重构结果依然获得很大改善。

关键词：压缩感知；后验信息；正交匹配追踪；单像素相机；近似矩阵

中图分类号：TP391.41 DOI：10.16375/j.cnki.cn45-1395/t.2023.04.002

0 引言

根据奈奎斯特采样定理，当采样频率达到信号最高频率的2倍及以上时才能精确地重构出原始信号。压缩感知理论的出现打破了这一局面，它的核心是减少测量点数，实现对原始信号的精确重构，并且在采集信号的同时对信号进行高压缩[1]。因此，压缩感知一经出现就在超分辨率显微镜[2-3]、遥感[4-5]、磁共振成像[6]、电子计算机断层扫描[7]和图像处理[8-9]等领域崭露头角。

Duarte等[10-12]基于压缩感知理论提出的单像素相机中，其核心部件是数字微镜器件（digital micromirror decive，DMD）。DMD上微镜的翻转可以表示为0或1，0表示微镜不能将光反射到单像素摄像头，1表示微镜可以将光反射到单像素摄像头。单像素摄像头通过DMD采集和压缩数据。单像素相机的测量矩阵通过编程控制DMD上微镜的翻转来表示0-1随机矩阵或0-1循环矩阵。相较于0-1循环矩阵，0-1随机矩阵具有更好的随机性，但不利于编程实现。0-1循环矩阵的随机性不足，但胜在更易于编程实现。这2种矩阵所需存储空间小而且运算速度快。

2 基于相邻列相减压缩感知模型的重构结果

对原始图像的压缩感知测量数据作相邻列相减处理，然后基于式（7）采用OMP算法求解重构，最后再对重构结果作相邻列相加得到最终重构图像。

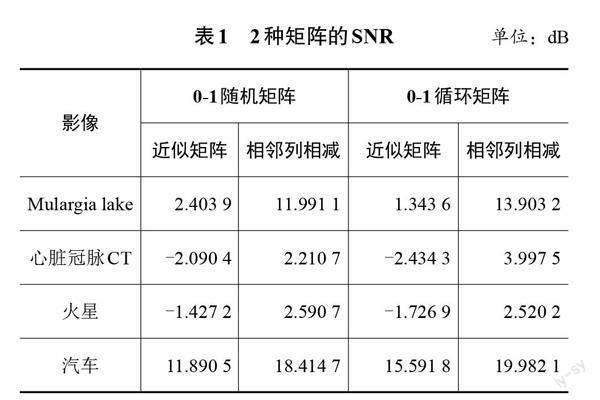
图1、图2和表1是基于相邻列相减压缩感知模型对遥感影像Mulargia lake、心脏冠状动脉CT影像、火星以及汽车的重构结果。Mulargia lake是意大利撒丁岛Mulargia湖的2个遥感影像的差值图，由Landsat-5卫星在波段4分别拍摄于1995年9月和1996年7月。该图反映了Mulargia湖水位上升而造成的陆地淹没情况。为满足稀疏条件，对2个时相的原始遥感影像作简单处理，差值图中未变化区域的灰度值都为0。

图1和图2中从左往右，第一列是近似矩阵的重构结果，第二列是近似矩阵采用相邻列相减压缩感知模型的重构结果，第三列为原始图像。对比第一列和第二列的图像可以清楚地看到，近似矩阵采用相邻列相减压缩感知模型的重构效果远远好于近似矩阵的重构效果。第一列图像有模糊不清的条带，第二列图像虽没有第一列图像的模糊不清，但是多了许多条纹，而且条纹范围大。这些条纹极大地影响了图像的重构效果，若能降低条纹的影响，会得到更好的重构效果。

为了更加直观地比较重构图像效果，本文用信噪比（signal to noise ratio，SNR）来表示图像的重构效果。SNR计算公式如式（8）所示，

（8）

式中：SNR表示SNR的值；[x]是真实信号，[x∈RN]；[xR]表示[x]的重构结果；[||?||2]表示向量的模。

从表1中可以看出，相邻列相减压缩感知模型对这4幅图像均有提升。其中对Mulargia lake图像的提升最大，0-1随机矩阵的SNR能提高约9.6 dB，0-1循环矩阵的SNR能提高约12.6 dB。对火星图像的提升最小，0-1随机矩阵的SNR仅能提高约4.0 dB，0-1循环矩阵的SNR仅能提高约4.2 dB。

尽管该模型能提高重构效果，但是该模型也有缺陷，使用该模型重构图像会有很显著的条纹影响，这些条纹无法避免，只能采取某些方法降低它的影響。该模型的本质是利用图像相邻列像素值一般不发生突变甚至有少许值是一样的这一特点，将相邻列像素值相减，让列变得更为稀疏。即使有些列变得更为稀疏了，但对于OMP算法，仍然会有重构误差，不能非常精确地重构出来。该模型重构图像的最后一步是通过相邻列相加来还原图像，因此，对于有重构误差的列，在相邻列相加之后，重构误差会逐渐累积，导致越靠后，偏差累积的越多，条纹越明显。图1和图2中第2列图像的条纹正是由于这个原因引起的，而且这些条纹越靠右越清晰可见。

3 基于后验信息的压缩感知重构

当原始图像灰度矩阵的某些列足够稀疏的时候，OMP算法可以获得更好的重构结果。基于后验信息的压缩感知重构详细算法：1）基于式（2）逐列采集得到测量数据y；2）通过OMP算法重构得到Δx，并计算前文后验信息中的判断值m，将Δx分为重构好的列与重构不好的列；3）根据测量数据y采用相邻列相减压缩感知模型，并用OMP算法重构得到x；4）将Δx中重构不好的列替换成x中的对应列，从而得到基于后验信息的压缩感知重构结果X。

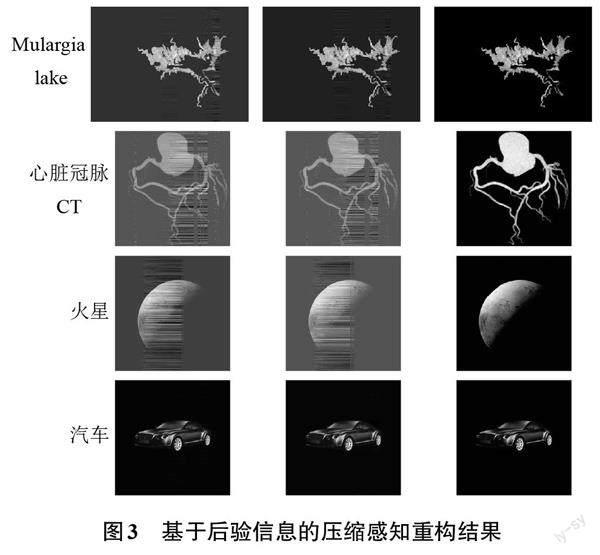
基于后验信息的压缩感知重构结果如图3所示。从左至右第一列图像是0-1随机矩阵的近似矩阵重构结果，第二列图像是0-1循环矩阵的近似矩阵重构结果，第三列图像是原始图像。对比图3与图1、图2可知，基于后验信息的压缩感知重构结果的条纹影响更小，重构效果更好。

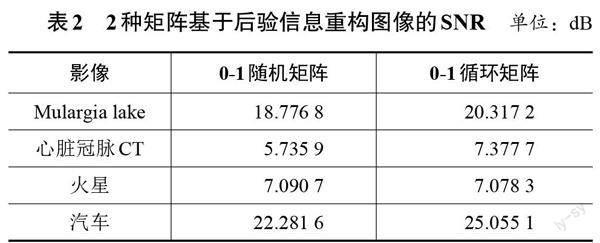
基于后验信息重构图像的2种矩阵的SNR结果如表2所示。对比表2和表1可知，相较于近似矩阵，基于后验信息重构的0-1随机矩阵和0-1循环矩阵，对于Mulargia lake图像，其SNR分别提高了约16.4、19.0 dB；对于心脏冠脉CT图像，其SNR分别提高了约7.8、9.8 dB；对于火星图像，其SNR分别提高了约8.5、8.8 dB；对于汽车图像，其SNR分别提高了约10.4、9.5 dB。由此可知，基于后验信息的压缩感知重构对这4幅图像的SNR均有较大提升。

基于后验信息的压缩感知重构在一定程度上降低了相邻列相减压缩感知模型带来的条纹影响，但是只适用于类似于这4幅图的稀疏图像。对于不稀疏的图像，因为受限于OMP算法只对足够稀疏的信号有很好的重构结果，所以該方法的重构图像会受到更为显著的条纹影响，而且重构效果不好。

4 结论

本文提出了在重构稀疏图像时判断OMP算法重构好坏的后验信息、相邻列相减压缩感知模型以及基于后验信息的压缩感知重构方法，并通过实验给出判断经验式作为后验信息。虽然该模型在OMP算法重构上会有明显的条纹，但是重构结果依然有很大的改善。基于后验信息的压缩感知重构方法充分利用了发现的后验信息，进一步提高重构效果。该方法只使用了OMP算法，具有OMP算法计算速度快的优点，且SNR得到较大提高，但是该方法对不稀疏的图像不适用。

参考文献

[1] DONOHO D L.Compressed sensing[J].IEEE Transactions on Information Theory，2006，52（4）：1289-1306.

[2] CHENG T，CHEN D N，YU B，et al.Reconstruction of super-resolution STORM images using compressed sensing based on low-resolution raw images and interpolation[J].Biomedical Optics Express，2017，8（5）：2445-2457.

[3] ZHU L，ZHANG W，ELNATAN D，et al.Faster STORM using compressed sensing[J].Nature Methods，2012，9（7）：721-723.

[4] YIN X Q，QIAN J S，GUO X G，et al.Compressed sensing of remote image based on photograph LDPC codes matrix[J].Journal of Intelligent and Fuzzy Systems，2019，37（4）：4605-4613.

[5] 辛蕾，李峰，鲁啸天，等.面向光学遥感影像的高效编码与重构[J].光学精密工程，2021，29（12）：2956-2963.

[6] FESSLER J A.Optimization methods for magnetic resonance image reconstruction：key models and optimization algorithms[J].IEEE Signal Processing Magazine，2020，37（1）：33-40.

[7] PERELLI A，LEXA M，CAN A L，et al.Compressive computed tomography reconstruction through denoising approximate message passing[J].SIAM Journal on Imaging Sciences，2020，13（4）：1860-1897.

[8] LIANG Z Y，YU D B，CHENG Z D，et al.Compressed sensing fourier single pixel imaging algorithm based on joint discrete gradient and non-local self-similarity priors[J].Optical and Quantum Electronics，2020，52（8）：1-15.

[9] QIN S.Simple algorithm for L1-norm regularisation-based compressed sensing and image restoration[J].IET Image Processing，2020，14（14）：3405-3413.

[10] DUARTE M F，DAVENPORT M A，TAKHAR D，et al.Single-pixel imaging via compressive sampling[J].IEEE Signal Processing Magazine，2008，25（2）：83-91.

[11] EDGAR M P，GIBSON G M，PADGETT M J.Principles and prospects for single-pixel imaging[J].Nature Photonics，2019，13（1）：13-20.

[12] 吴小龙，程涛，杨明.单像素相机内部元素对重构矩阵性能的影响[J].广西科技大学学报，2021，32（1）：71-77.

[13] CANDES E J，PLAN Y.A probabilistic and RIPless theory of compressed sensing[J].IEEE Transactions on Information Theory，2011，57（11）：7235-7254.

[14] 柯钧，张临夏，周群.压缩感知在光学成像领域的应用[J].光学学报，2020，40（1）：98-123.

[15] ELAD M.Optimized projections for compressed sensing[J].IEEE Transactions on Signal Processing，2007，55（12）：5695-5702.

[16] DUARTE-CARVAJALINO J M，SAPIRO G.Learning to sense sparse signals：simultaneous sensing matrix and sparsifying dictionary optimization[J].IEEE Transactions on Image Processing，2009，18（7）：1395-1408.

[17] 程濤，朱国宾，刘玉安.基于0-1稀疏循环矩阵的测量矩阵分离研究[J].光学学报，2013，33（2）：172-177.

[18] CHENG T.Reconstruction improvement of single-pixel camera based on operator matrix-induced compressive sensing[J].Geodetski List，2020，74（3）：283-296.

[19] 魏子然，张建林，徐智勇，等.一种基于单像素相机的压缩感知图像重建优化算法[J].半导体光电，2019，40（3）：449-454.

[20] SHIN Z Y，LIN H S，CHAI T-Y，et al.Programmable spatially variant single-pixel imaging based on compre-

ssive sensing[J].Journal of Electronic Imaging，2021，30（2）：1-15.

[21] TROPP J A，GILBERT A C.Signal recovery from random measurements via orthogonal matching pursuit[J].IEEE Transactions on Information Theory，2007，53（12）：4655-4666.

[22] 吴小龙，伍松.一种改进的变步长OMP图像重建算法[J].广西科技大学学报，2019，30（4）：64-69，76.

Compressed sensing image reconstruction method

based on posterior information

LI Degao， CHENG Tao*， XU Cong， WANG Yingshan

（School of Mechanical and Automotive Engineering， Guangxi University of Science and Technology， Liuzhou 545616， China）

Abstract： The measurement data of a single pixel camera can be reconstructed with the orthogonal matching pursuit （OMP） algorithm， which， however， generates reconstructed images of non-desirable quality. We propose a method to improve the image reconstruction. We can judge the quality of the reconstruction using prior information （column modulus mean value） in this method. The sparsity is enhanced by subtraction of adjacent columns of measurement data. Firstly， measurement data are reconstructed column by column based on OMP. Secondly， for columns with poor reconstruction results， subtraction of adjacent columns is conducted and then they are reconstructed one by one. Finally， better-reconstructed images are obtained through accumulating column by column. The experimental results show that this method can significantly improve the signal to noise ratio （SNR） of reconstructed images when only OMP is used. Although there are obvious stripes on the reconstructed images， significant improvement is still achieved in the reconstruction.

Key words： compressed sensing; posterior information; orthogonal matching pursuit; single-pixel camera; approximate matrix

（责任编辑：黎 娅）

收稿日期：2022-12-17

基金项目：广西自然科学基金项目（2022GXNSFAA035593）；国家自然科学基金项目（41461082，81660296）资助

第一作者：李德高，在读硕士研究生

*通信作者：程涛，博士，研究员，研究方向：压缩感知和遥感，E-mail：ctnp@163.com