翼伞系统在复杂环境下的组合式归航轨迹规划

何伟朝　文家燕　赵旭东　闻海潮

摘 要：在较为复杂的空投环境中进行翼伞系统归航任务时，必须考虑风场以及复杂地形的影响。针对该问题，本文将翼伞空投区域分为障碍区、过渡区以及着陆区，并提出一种基于风场下的复杂多约束条件的翼伞系统组合式航迹规划策略。在该方法中，将障碍区的复杂地形环境约束转化为实时路径约束，借助风场干扰下的翼伞系统模型，把控制量消耗最小作为目标函数并采用高斯伪谱法进行求解；为了使翼伞系统能更平滑精准地到达目标点，设立过渡区以实现翼伞系统控制量调整，并在着陆区采用分段归航的方式设计归航轨迹；最后基于改进Tent映射的混合混沌粒子群算法求解目标参数。仿真结果表明：与高斯伪谱法直接归航对比，本文方法规划出的航迹具有更好的可行性和实用性；与传统混沌粒子群算法相比，本文的改进混沌粒子群算法具有更好的收敛性，规划出的翼伞航迹具有更高的精准度。

关键词：翼伞系统；航迹规划；复杂环境；高斯伪谱法；分段归航；粒子群算法；改进Tent映射

中图分类号：TP273；V249 DOI：10.16375/j.cnki.cn45-1395/t.2023.04.014

0 引言

翼伞系统是一种可以依靠开伞后冲压空气形成的气室来维持翼型，并提供升力和前进力的柔性飞行器[1]，具有良好滑翔性、可控性和稳定性。翼伞系统可以通过下拉操纵绳以改变翼伞在空中的姿势，从而精确控制整个系统航向。但传统降落伞系统只能随风而动[2]，不受控制。随着我国综合国力的不断增强，翼伞系统以其特殊的结构，以及在飞行稳定性、承载能力、优良的气动特性方面的巨大优势[3]，使得翼伞技术在航天、救灾、定点空投等领域发挥着不可替代的作用[4]。翼伞系统在实际空投环境中的归航策略大致上分为2种：一种是考虑复杂环境制约的最优控制归航策略，比如罗淑贞等[5-6]使用伪谱法把最优控制航迹规划转变为非线性规划问题，再利用序列二次规划算法求解；孙昊等[7]将翼伞系统的六自由度（6-degrees of freedom，6-DOF）动力学模型引入翼伞归航的轨迹规划中，并采用改进高斯伪谱法解决了传统质点模型所规划的目标轨迹难以满足复杂环境下的系统动力学约束问题。另一种是不考虑障碍约束的分段归航策略，比如熊菁[8]将翼伞系统归航轨迹分为3段，采用改进的遗传算法对其进行优化；陶金等[9]采用量子遗传算法对翼伞系统的归航轨迹进行优化；Guo等[10]针对未知侧向风干扰，提出一种考虑恒定风的高空分段归航算法；Sun等[11]将最优归航思想运用到分段归航中，提出一种最优分段归航策略，并运用量子遗传算法进行优化。以上研究都在不同方向上取得一定的成果，但在现实空投环境中，存在山峰、禁飞区以及风场等复杂环境的干扰，难以采用单一的分段归航或者最优归航策略。实际上，在空投环境中，目标点周围会有一小范围没有障碍物，如此就可以采用组合式归航策略。李宇辉等[12]基于此思想将翼伞的空投环境大致分为障碍区和着陆区2个区域，分别采用快速搜索随机树算法和遗传算法求解目标参数，同时还考虑了2段航迹的衔接问题，其研究成果能够实现2段航迹的过渡，并最终顺利完成翼伞的航迹规划。但存在一些局限性，如在翼伞避障阶段没有考虑突然风的影响，在着陆阶段没有考虑平均风对航迹的影响，也没有考虑2段航迹切换时的控制量的变化，最后在着陆区采用传统遗传算法优化参数时，容易陷入局部最优。

为了解决以上问题，本文将翼伞空投环境进一步划分为障碍区、过渡区以及着陆区。在障碍区将风场干扰以及避障完成后的可行区域等问题考虑进去，建立合适的翼伞运动模型，构造出带有复杂约束条件的以控制量为优化目标的最优控制问题，再通過高斯伪谱法把优化问题转化为容易求解的非线性规划问题，利用二次规划算法求出最优飞行轨迹。完成避障后，调整控制量渡过过渡区。翼伞进入着陆区后，在障碍物较少或无障碍物情况下，可采用控制过程更加简单的分段归航法，并通过改进的混合混沌粒子群算法进行轨迹优化。

1 复杂环境下翼伞系统建模

1.1 翼伞系统质点模型

翼伞系统通常由伞体和负载组成，若把伞体和负载看作刚性连接整体的话，可以建立六自由度（6-DOF）刚体模型。进一步分析翼伞与有效负载之间的相对运动，则可以建立7-DOF、8-DOF以及更高自由度的翼伞系统动力学模型。但模型自由度越高，其计算复杂度也相对越高[13]，因此研究翼伞系统整体的归航轨迹时，可把系统整体视为质点，采用翼伞质点模型以便更好进行航迹规划。

3 仿真及分析

为验证本文所设计的归航策略能使翼伞系统在风场干扰下实现避障，能平稳地从障碍区到达着陆区，并顺利抵达目标点，现利用提出的组合式航迹规划策略进行仿真，再将其结果与直接高斯伪谱法归航策略进行对比。

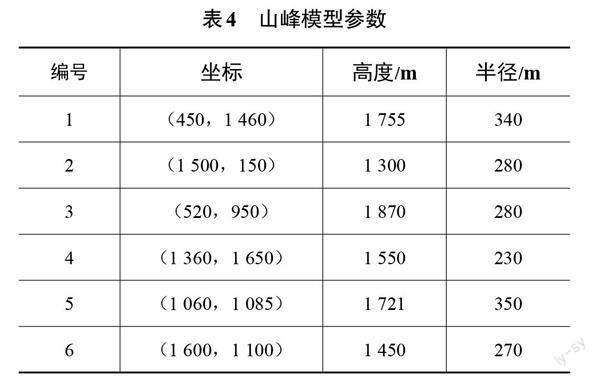
设定翼伞系统虚拟目标点坐标为[（-400， 0， 0）]，实际目标点坐标为[（0， 0， 0）]，初始投放点的位置为[（3 000， 3 000， 2 000）]，系统允许最小转弯半径[Rmin=100] m，滑翔比[f=3]，着陆区半径[Rth=800] m，水平速度[vs=15] m/s，垂直速度[vc=5] m/s，通过过渡区后的末端角度[αe=-π/3]。目标点附近风向设定为沿[x]轴为正方向，风速[vw=2] m/s。本文山峰模型的中心点位置分别为[（1 500， 1 500）]、[（1 500， 0）]、[（2 000， 2 500）]、[（2 500， 1 000）]、[（500， 1 500）]、[（1 000， ]

[3 000）]、[（3 200， 2 300）]，每座山峰高度均为2 000 m，山体半径均为400 m。

同时，为了方便与本文的组合式策略作对比，初始条件、障碍山峰设置不变，其末端角度需满足逆风对准的条件，故设置为[αf=π]或[αf=-π]。按照以上设定条件进行仿真，得到的归航轨迹结果如图3所示。

由图3（a）、（b）中的实线可看出，翼伞在障碍区归航过程中受到突风干扰后，调整航向角避开山峰，最终能够完成避障任务并进入过渡区；过渡区内翼伞系统进行控制量调整后，到达着陆区，然后切换为分段归航方式；由于受到横向常值风影响，整体航迹最终转化为横向偏移，即翼伞最终会降落在实际目标点处，实现逆风着陆，且落点精度较高。由此可以看出翼伞系统整体航迹较为平滑，下降趋势较为平缓，没有出现高度突然骤降的情况。而从图3中虚线可看出，虽然采用直接归航策略的翼伞系统最后到达了目标位置，但是过程中出现高度骤降情况，且明显没有完全避开障碍物，可以从黑色方框处看出翼伞系统从接近着陆区的山峰旁擦边穿过。

2种策略的系统航向角对比如图4所示。

从图4中可以看出，组合式归航策略耗时较多，控制翼伞飞行较久，但其中航角变换也比较平缓，航向角曲线整体较平滑，这样的航角变化曲线更利于实际中的跟踪控制；相较之下，直接归航策略中的航角变化存在小幅度振荡，且较为陡峭，不太适合实际过程中的跟踪控制。

表1为2种航迹规划的对比结果。

由表1可以看出，高斯伪谱法最优航迹规划策略在能量消耗以及精准降落方面要优于本文的组合式归航策略，但直接归航不一定能完全实现避障功能，在接近着陆区时，有可能会碰撞到山峰，且整个归航过程需要不断地控制电机进行调整，控制量仍会发生不同程度震荡，从实际工程考虑，控制难度很大，整个归航过程难以实现。而本文采用的组合式归航策略，虽然其中的分段归航策略部分耗能略高，但由于翼伞在成功避障后进行一段时间的控制量调整，进入着陆区内，障碍物较少且距离目标点较近，此时应将翼伞系统精确降落以及平缓降落作为首要考虑因素，故此时选用的分段归航策略的控制量为分段常值，控制操作要比最优归航简单很多，且整个归航过程也容易在实际工程中实现。

为验证本文改进的混沌粒子群算法能更好地优化分段归航的参数，使用其作为优化工具，对着陆区部分的翼伞系统归航轨迹进行仿真实验，并与文献[20]中基于Logistic混沌粒子群算法所优化的翼伞归航轨迹进行对比。

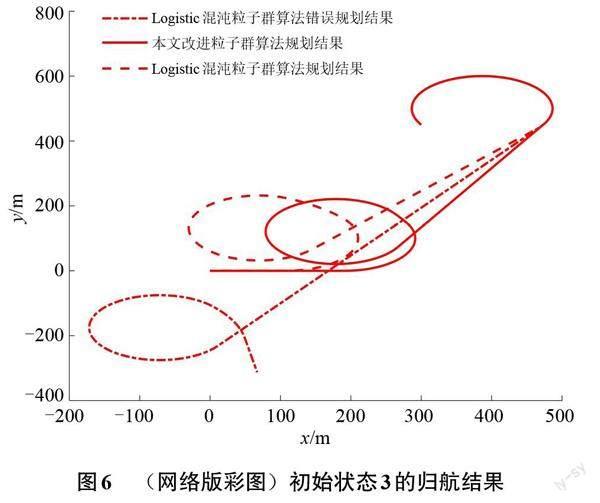
设定各翼伞系统初始参数为：水平速度[vs=13.8] m/s，垂直速度[vc=4.6] m/s，最小转弯半径[Rmin=100] m，滑翔比[f=3]。着陆区约束条件设置为：[Rep∈[230， 500]]，[βi（i=1， 2， 3， 4）∈[0， π]]，并设置3种初始运动状态如表2所示，其中状态1表示初始点离目标点适中的情况，状态2表示初始水平位置离目标点较近但高度较高的情况，状态3表示水平位置离目标点较近但高度较低但能实现归航的情况。得到的仿真結果为：误差结果如表3所示，2种算法最佳适应度迭代曲线如图5所示，以初始状态3为例的归航结果如图6所示。

图5为改进Tent混沌粒子群算法以及Logistic混沌粒子群算法在进行航迹优化时的最佳适应度迭代曲线。由虚点线和实线可以看出，基于Logistic混沌粒子群算法会在43代左右表现出比改进Tent混合混沌粒子群算法更快的收敛性，但利用其优化结果进行航迹规划的结果如图6所示，是优化错误的结果。从图5中实线和虚线的对比可以看出本文改进的粒子群算法能表现出更好的收敛速度和全局搜索能力。

表3列出了上述3种初始状态下分别采用本文中改进Tent混沌粒子群算法进行30次翼伞系统归航轨迹规划的终端时刻着陆点距离目标点的偏差平均值，并同时列出文献[20]中使用的Logistic混沌粒子群算法进行30次航迹规划的结果。从表中数据可以看出，改进Tent混沌粒子群算法和Logistic混沌粒子群算法都能使翼伞系统在目标点着陆，但改进Tent混沌粒子群算法所规划的航迹精度更高。值得注意的是，在初始条件3下的基于Logistic混沌粒子群算法规划结果出现较大误差，这是由于有几次算法寻优出现错误，使得优化半径参数出现负值，从而出现如图6中点线的错误航迹规划结果。

最后，为使得本文的归航策略能适用于更具有一般性的场景，将障碍山峰设置为如表4所示，其他初始条件按状态3设置，得到结果如图7所示。

从图7（a）、（b）中可以看出，本文算法在一般环境下，也能使翼伞顺利完成避障并精准到达目标点。

4 结论

本文根据实际情况，将翼伞空投区域分为障碍区、过渡区以及着陆区，并在翼伞归航全程考虑风场的影响，提出一种复杂环境下多约束条件的组合式归航策略，通过仿真对比后得出以下结论：

1）障碍区内考虑了突风的影响，在障碍区采用具有更好避障归航能力的高斯伪谱法来实现突风影响下的翼伞系统避障任务。得到的归航曲线较为平滑，在突风的干扰下，航向角没有大幅度跳变，整体较为平稳，体现出算法的鲁棒性较好，能够较好地完成避障任务。

2）着陆区内考虑到常值风的影响，建立虚拟着陆点，将整个分段归航过程中风的影响转化为着陆点的偏移，并采用收敛性更好、优化结果更稳定的改进Tent混沌粒子群算法对轨迹进行优化。与Logistic混沌粒子群算法对比，仿真结果表明，本文算法优化翼伞参数的收敛速度更快，且规划出的翼伞系统的最终落点精度更高。

由于现实中的风场是实时变化的，其对翼伞系统的影响也应该是实时变化的，所以未来可以将基于风场预测的航迹规划作为一个重要研究内容。

参考文献

[1] LUO S Z，SUN Q L，TAN P L，et al. Soft landing control of unmanned powered parafoils in unknown wind environments[J]. Proceedings of the Institution of Mechanical Engineers，Part G：Journal of Aerospace Engineering，2019，233（3）：949-968.

[2] SUN H，LUO S Z，SUN Q L，et al. Trajectory optimization for parafoil delivery system considering complicated dynamic constraints in high-order model[J]. Aerospace Science and Technology，2020，98：105631.

[3] GAO H T，TAO J，DEHMER M，et al. In-flight wind field identification and prediction of parafoil systems[J]. Applied Sciences，2020，10（6）：1958.

[4] YU Z P，TAN P L，SUN Q L，et al. Longitudinal wind field prediction based on DDPG[J]. Neural Computing and Applications，2021，34（1）：227-239.

[5] 罗淑贞，孙青林，檀盼龙，等. 基于高斯伪谱法的翼伞系统复杂多约束轨迹规划[J]. 航空学报，2017，38（3）：220-230.

[6] LONG X Y，SUN M W，PIAO M N，et al. Parameterized trajectory optimization and tracking control of high altitude parafoil generation[J]. Energies，2021，14（22）：7460.

[7] 孙昊，孙青林，滕海山，等. 复杂环境下考虑动力学约束的翼伞轨迹规划[J]. 航空学报，2021，42（3）：372-381.

[8] 熊菁. 翼伞系统动力学与归航方案研究[D]. 长沙：国防科学技术大学，2005.

[9] 陶金，孙青林，朱二琳，等. 基于遗传算法带约束的翼伞系统归航轨迹设计[J]. 中南大学学报（自然科学版），2017，48（2）：404-410.

[10] GUO Y M，YAN J G，WU C H，et al. Autonomous homing design and following for parafoil/rocket system with high-altitude[J]. Journal of Intelligent and Robotic Systems，2021，101（4）：1-15.

[11] SUN H，SUN Q L，CHEN Z Q，et al. An optimal‐multiphase homing methodology for powered parafoil systems[J]. Optimal Control Applications and Methods，2020，41（4）：1118-1142.

[12] 李宇辉，赵敏，陈奇，等. 复杂环境下翼伞系统的组合式航迹规划[J]. 航空学报，2021，42（6）：556-567.

[13] 孙昊，刘雪峰，刘靖雷，等. 大规模空投中的多翼伞一致性控制算法[J]. 控制理论与应用，2021，38（12）：1993-2000.

[14] 王康，谭继可，周绪红，等. 基于知识图谱的海上浮式风机领域可视化分析[J]. 哈尔滨工程大学学报，2021，42（9）：1303-1311.

[15] SUN Z Y，ZHANG B，ZHANG J A，et al. Examination of surface wind asymmetry in tropical cyclones over the northwest pacific ocean using SMAP observations[J]. Remote Sensing，2019，11（22）：2604.

[16] 陈家宝，文家燕，谢广明. 基于改进A*算法的移动机器人路径规划[J]. 广西科技大学学报，2022，33（1）：78-84.

[17] TANG X J，WEI J L，CHEN K. A chebyshev-gauss pseudospectral method for solving optimal control problems[J]. Acta Automatica Sinica，2015，41（10）：1778-1787.

[18] 张海江，文家燕，谢广明，等. 飽和约束下事件触发多智能体系统量化通信环形编队控制[J]. 广西科技大学学报，2022，33（4）：44-50，69.

[19] CHO N，LEE S，KIM J，et al. Wind compensation framework for unpowered aircraft using online waypoint correction[J]. IEEE Transactions on Aerospace and Electronic Systems，2020，56（1）：698-710.

[20] 陶金. 复杂环境下翼伞系统的建模与归航控制研究[D]. 天津：南开大学，2017：88-97.

Combined homing trajectory planning of a parafoil system

in complex environment

HE Weichao1， WEN Jiayan1， 2， ZHAO Xudong*1， 3， WEN Haichao1

（1. School of Automation， Guangxi University of Science and Technology， Liuzhou 545616， China; 2. Guangxi Key Laboratory of Automobile Components and Vehicle Technology （Guangxi University of Science and Technology）， Liuzhou 545616， China; 3. Faculty of Electronic Information and Electrical Engineering， Dalian University of Technology， Dalian 116024， China）

Abstract： When the parafoil system homing mission is carried out in a complex airdrop environment， the effects of wind field and complex terrain must be considered. To solve this problem， a combined trajectory planning strategy of parafoil system based on complex multi constraint conditions in wind field are proposed， in which the parafoil airdrop is divided into an obstacle area and a landing area. In this method， the complex terrain environment constraints in the obstacle area are transformed into real-time path constraints. With the help of the parafoil system model under the interference of wind field， the minimum control consumption is taken as the objective function and solved by Gauss pseudo-spectral method; In order to make the parafoil system reach the target point more smoothly and accurately， a transition zone is set up to adjust the control quantity of the parafoil system， and the trajectory is designed by means of multiphase homing in the landing zone. Finally， the target parameters are solved by hybrid chaotic particle swarm optimization algorithm on improved Tent map. The simulation results show that compared with Gauss pseudo-spectral homing， the proposed planned trajectory has better feasibility and practicability; Compared with the traditional chaotic particle swarm optimization algorithm， the improved chaotic particle swarm optimization algorithm has better convergence， and the planned parafoil trajectory has higher accuracy.

Key words： parafoil system; trajectory planning; complex environment; Gauss pseudo-spectral method; multiphase homing; particle swarm optimization; improved Tent map

（責任编辑：黎 娅）

收稿日期：2022-12-02

基金项目：国家自然科学基金项目（61963006）；广西自然科学基金面上项目（2018GXNSFAA050029，2018GXNSFAA274085）；广西自动检测技术与仪器重点实验室开放基金项目（YQ20208）资助

第一作者：何伟朝，在读硕士研究生

*通信作者：赵旭东，博士，教授，研究方向：航空发动机控制、切换系统控制、智能控制、鲁棒控制等，E-mail：xudongzhao@dlut.edu.cn