第二大符号距离特征值属于[-1,(17-)/2] 的符号图∗

杨博远，李丹

(新疆大学数学与系统科学学院，新疆乌鲁木齐 830017)

0 引言

符号图Σ=(G,σ) 是由它的底图G=(V,E) 与符号函数σ:E→{-1,1} 组成. 在符号图中, 用±1 来表示边的符号. 设M=M(Σ) 为符号图Σ=(G,σ) 的实矩阵, 且PM(λ)=det(λI-M) 是M-多项式. 一个矩阵的全部特征值(包括重数) 集合称为该矩阵的谱, 称M的谱为符号图Σ 的M-谱. 一般的, 将M的谱表示为λ1(M)≥λ2(M)≥···≥λn(M). 矩阵M特征值模的最大值称为矩阵M的谱半径. 用u∼v表示顶点u与v相邻, 用u≁v表示顶点u与v不相邻. 定义Σ 中路径P的符号为σ(P)=Πe∈E(P)σ(e). 设P(u,v)是顶点u与v之间的最短路径, 令P(u,v)={P(u,v)|{u,v}⊂V(G)}. 顶点u与v之间最短路径的长度定义为u与v之间的距离, 用duv表示. 图G的直径是图G中所有顶点间距离的最大值, 记作diam(G). 符号图Σ 的直径即为其底图G的直径. 邻接矩阵A=A(Σ)=(aij) 是n×n阶矩阵, 其中若vi∼vj, 则aij=σ(vivj), 否则等于0. 符号图最初是由Harary[1]用于研究社交网络模型而引入. 随后Zaslavsky[2]应用了符号图的一种等价性. Chaiken[3]和Zaslavsky[2]分别得出了符号图的矩阵-树定理. Harary[1]也给出了符号图平衡性的概念. 如果符号圈包含偶(奇)数条负边, 则称其是正(负) 圈. 若符号图的所有圈均为正, 则称其为平衡的; 否则称其为非平衡的. 一般图可以看作是(平衡的) 符号图, 其中所有边均为正. Koledin 等[4]在给定阶数、边数以及负边个数的符号图类中研究了最大邻接特征值达到最大的连通符号图. 设Un(或Bn)分别表示非平衡的n阶单(或双) 圈符号图的集合.Akbari 等[5]在Un中研究了最大邻接特征值达到最大的符号极图. Souri 等[6]在给定围长的符号单圈图类中刻画了最大邻接特征值达到最大的符号图. 当n≥36 时, He 等[7]在Bn中研究了最大邻接特征值前五大的符号图.Belardo 等[8]在Un和Bn中分别考虑了谱半径达到最大和最小的符号图.

令σmax(u,v)=max{σ(P(u,v))|P(u,v)∈P(u,v)},σmin(u,v)=min{σ(P(u,v))|P(u,v)∈P(u,v)} 及dmax(u,v)=σmax(u,v)d(u,v),dmin(u,v)=σmin(u,v)d(u,v). Hameed 等[9]给出了符号图的两类距离矩阵的定义:

与

设u,v∈V(Σ), 若dmax(u,v)=dmin(u,v), 则称u和v是距离-可兼容的(简称为可兼容的). 如果Σ 中任意两个顶点都是可兼容的,则称Σ 是可兼容的,此时令Dmax(Σ)=Dmin(Σ):=D±(Σ). 设D(G)=(duv)n×n是连通图G的距离矩阵. 如果Σ 的所有边都是正的, 显然Dmax(Σ)=Dmin(Σ)=D(G). Shijin 等[10]利用因子图的符号距离矩阵研究了符号图乘积的符号距离矩阵, 如Cartesian 积和Lexicographic 积, 此外还讨论了一些特殊符号图乘积的距离谱. 对应符号图的两类符号距离矩阵, Roy 等[11]定义了两类符号距离Laplacian 矩阵, 利用这些矩阵刻画了符号图的平衡性,并且得到了一些非平衡符号图类的符号距离Laplacian 谱.最近, Li 等[12]给出了关于直径至少为2 的符号图最小距离特征值的上界.

距离特征值的研究可以追溯到Graham 等[13]关于负的距离特征值个数与处理数据通讯系统问题之间关系的研究. 生成路和生成圈分别称为Hamilton 路和Hamilton 圈. Lin 等[14]在不含Hamilton 圈的n阶连通图类中, 刻画了距离谱半径达到最小的图. 用Sn表示n阶星图. 图G的独立数α(G) 是指G中最大独立集的顶点数. Fajtlowicz[15]提出了关于距离特征值和图不变量的猜想: 设图G是独立数α(G) ≤2 的连通图, 那么λ2(D(G))≤tr(G), 其中tr(G) 表示图G中三圈的个数. Lin[16]证明了该猜想. 图Sn,p+1是在星图Sp+1和星图Sn-p-1的最大度点之间加一条边得到的n阶双星图, 其中1 ≤p≤⎿(n-2)/2」. 在图G每对距离至多为k的顶点之间加一条边得到的(简单) 图称为图G的k次幂, 记作Gk. Xing 等[17]刻画了的树, 并且给出了连通图k次幂的第二大距离特征值的下界. Lin[18]得到了与直径有关的λ2(D(G)) 的上界. Xue等[19]给出了第二大距离特征值不超过-(1/2) 的所有块图. Xing 等[20]刻画了的所有n阶连通图. Liu 等[21]刻画了的所有n阶连通图. 受以上研究的启发,本文主要考虑以下问题.

问题1第二大距离特征值属于的全部连通符号图有哪些?

1 准备知识

除非另有说明, 否则本文中符号图的底图均简单且连通.

引理1[9]符号图的下列性质是等价的.

(1) Σ 是平衡的;

引理2(Cauchy 交错定理) 设A是n阶Hermitian 矩阵,B是A的m阶主子阵. 如果λ1(A)≥λ2(A)≥···≥λn(A) 是A的特征值,µ1(B)≥µ2(B)≥···≥µm(B) 是B的特征值, 那么λn-m+i(A)≤µi(B)≤λi(A), 其中i=1,···,m.

2 主要结论

设Kn,Pn和Cn分别表示n阶的完全图, 路以及圈. 设Σ = (G,σ) 是符号图. 若G不包含H作为其导出子图, 则称H是G的禁用子图. 顶点u在V(G) 中的邻点集用NG(u) 表示. 顶点u的闭邻点集是N[u]=N(u)∪{u}. 对于顶点子集S⊆V(G), 顶点v在顶点集S中的邻点集用NS(v) 表示. 用G[S] 来表示由S导出的G的子图. 若G[S] 是完全图, 则称S为团. 设dG(u)=|NG(u)| 是u在G中的度. 为了证明的方便,令

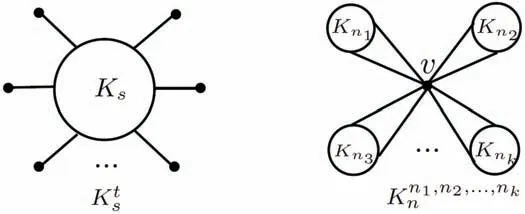
图1 和

定理1设Σ 是n≥2 阶连通符号图. 如果那么Σ 是平衡的或者是平衡的或者是平衡的

证明将通过以下断言来证明结论.

断言1所有的三圈都是平衡的.

否则,存在一个非平衡的三圈(见图2)作为Σ 的导出子图,那么Σ 的第二大距离特征值一定大于或等于非平衡三圈的第二大距离特征值. 注意到非平衡三圈的第二大距离特征值等于1. 由引理2 可知及产生矛盾.

图2 P5, C3 ∼C5, H1 ∼H3

断言2Σ 的每一个符号完全子图都是平衡的.

设(Ks,σ) 是Σ 的一个符号完全子图. 如果s=1 或2, 那么结论显然成立. 如果s=3, 那么由断言1 可知(K3,σ) 平衡. 下面只需考虑s≥4. 若(Ks,σ) 是Σ 的非平衡符号完全子图, 则首先断言(Ks,σ) 的最短负圈必为(C3,σ). 否则, 假设(Cl,σ) 是(Ks,σ) 的最短负圈, 其中Cl=v1v2v3v4···vlv1且l≥4. 注意到(Ks,σ) 是可兼容的, 故而如果σ12σ23=-1, 那么σ13=-1, 这表明C′=v1v3v4···vlv1是长度为l-1 的负圈, 产生矛盾. 如果σ12σ23=1, 那么σ13=1, 这表明C′′=v1v3v4···vlv1是长度为l-1 的负圈, 产生矛盾. 这与断言1 矛盾.因此, Σ 的每一个符号完全子图都是平衡的.

断言3(C4,σ), (C5,σ), (H1,σ), (H2,σ) 和(H3,σ) 是Σ 的禁用子图.

Ci,Hj如图2 所示, 其中i=4,5;j=1,2,3. 假设(C4,σ)⊂Σ, 令V(C4)={v1,v2,v3,v4}, 可得A1和B1分别是的主子阵, 其中对于A1的元素, 注意到如果σ12σ23= 1 或σ14σ34= 1, 那么σ13= 1, 如果σ23σ34= 1 或σ12σ14= 1, 那么σ24= 1. 对于矩阵B1, 如果但通过Matlab可得因此由引理2 可得及产生矛盾. 因此, (C4,σ) 是Σ 的禁用子图.

假设(C5,σ) ⊂Σ, 令V(C5) = {v1,v2,v3,v4,v5}, 于是可得A2和B2分别是的主子阵, 其中的元素, 注意到如果σ12σ23=σ23σ34=σ34σ45=1, 那么σ13=σ24=σ35=1. 对于矩阵B2, 如果但通过Matlab可得因此由引理2 可得及产生矛盾. 因此, (C5,σ) 是Σ 的禁用子图.

[45]张贤明：《从本土诉求到全球视野：当代中国政治学繁荣与发展的思考》，《贵州社会科学》2012年第3期。

假设(H1,σ)⊂Σ. 令V(P3)={v1,v2,v3}并且N(v1)∩N(v2)∩N(v3)={v4},可得A3和B3分别是和的主子阵, 其中 但通过Matlab 可得及因此由引理2 可得产生矛盾. 因此, (H1,σ) 是Σ 的禁用子图.

假设(H2,σ)⊂Σ,令V(P4)={v1,v2,v3,v4},v5与v2相邻. 可得A4和B4分别是的主子阵, 其中对于A4的元素, 注意到如果σ12σ23=σ23σ34=σ12σ25=σ23σ25=1,那么σ13=σ24=σ15=σ35= 1, 如果σ12σ23σ34=σ25σ23σ34= 1, 那么σ14=σ45= 1. 对于矩阵B4, 如果么但通过Matlab 可得因此由引理2 可得产生矛盾. 因此, (H2,σ) 是Σ 的禁用子图.

同理可得(H3,σ) 是Σ 的禁用子图.

断言4diam(G)≤3.

否则, 假设diam(G) ≥4, 那么(P5,σ) ⊂Σ, 并且令V(P5) = {v1,v2,v3,v4,v5}. 可得A5和B5分别是的主子阵, 其中对于A5的元素, 注意到如果σ12σ23=σ23σ34=σ34σ45=1, 那么σ13=σ24=σ35=1, 如果σ12σ23σ34=σ23σ34σ45=1, 那么σ14=σ25=1, 并且如果σ12σ23σ34σ45=1,那么σ15=1. 对于矩阵B5,如果那么如果那么并且如果那么但通过Matlab可得因此根据引理2 可得及产生矛盾.

情形1diam(G)=1. 显然, Σ 为符号完全图. 由断言2 可知Σ 平衡.

情形2diam(G)=2. 设G的直径路为P=v1v2v3.

断言5对于任意顶点u∈V(Σ){v1,v2,v3} 有u∈N(v1)∪N(v2)∪N(v3).

否则, 存在一点v4使得d(vk,v4)=2, 其中1 ≤k≤3. 从而存在一点w, 使得w∼v4且可得A6是的主子阵, 其中d(w,vk)=1 或2, 1 ≤k≤3, 并且注意到d(w,vk) 中至少有一个为1,aij=±1,1 ≤i≤4,2 ≤j≤5. 但通过Matlab 可得因此由引理2 可得及产生矛盾.

断言5 表明图G的任意一个顶点至少与v1,v2和v3中的一个相邻.

断言6N(v2)=V(Σ){v2}.

假设存在顶点u∈V(Σ){v2} 使得d(u,v2)=2. 如果u∼v1且u∼v3, 那么并有(C4,σ)⊂Σ, 这与断言3 矛盾. 如果u∼v1且u≁v3, 则存在另一顶点w使得uwv3是u与v3之间的最短路, 即d(u,v3)=2. 若w≁v1且w≁v2, 则并有(C5,σ)⊂Σ, 这与断言3 矛盾. 若w≁v1且w∼v2,则G[并有(C4,σ)⊂Σ,这与断言3 矛盾. 若w∼v1且w≁v2,则并有(C4,σ)⊂Σ, 这与断言3 矛盾. 若w∼v1且w∼v2, 则并有(H1,σ)⊂Σ, 这与断言3 矛盾. 关于u≁v1且u∼v3的情况是类似的. 故而u≁v1且u≁v3, 但这与断言5 矛盾.

令S1=(N(v1)∩N(v2))∪{v1,v2},S2=(N(v2)∩N(v3))∪{v2,v3}.

断言7G[S1],G[S2] 是符号完全图.

如果|S1| = 2 或3, 那么结论显然成立. 下面假设|S1| ≥4 且G[S1] 不是符号完全图. 设{u1,u2} ⊂N(v1)∩N(v2), 并且u1≁u2, 那么并有(H1,σ) 是Σ 的导出子图, 这与断言3 矛盾. 因此G[S1] 是符号完全图. 类似可得G[S2] 也是符号完全图.

断言8Σ-v2的每一个连通分支都是符号完全图.

令Σ1,Σ2,···,Σk是Σ-v2的k个连通分支. 如果v1∈V(Σi) 或v3∈V(Σi), 那么根据断言6 和断言7,Σi(1 ≤i≤k) 一定是符号完全图. 假设存在一个分支Σt使得v1,v3/∈V(Σt) 且Σt不是符号完全图, 那么由Σt连通可知|V(Σt)|≥3. 因此在Σt中存在一个顶点x有两个互不相邻的邻点y和z, 并且设P是y和z之间的一条二长路. 这表明(H1,σ)⊂Σ, 这与断言3 矛盾.

结合断言1∼8, 如果diam(G)=2, 那么Σ 是平衡的

情形3diam(G)=3. 假设G的直径路为P=v1v2v3v4.

断言9dG(v1)=dG(v4)=1.

由对称性不妨假设dG(v1)≥2, 那么存在另一顶点u使得u∼v1. 首先断言u≁v4, 否则分为以下3 种情况讨论. 若u≁v2且u≁v3, 则G[{u,v1,v2,v3,v4}]C5, 并有(C5,σ)⊂Σ, 产生矛盾; 若u≁v2且u∼v3(或u∼v2且u≁v3), 则G[{u,v1,v2,v3}]C4(或G[{u,v2,v3,v4}]C4), 并有(C4,σ)⊂Σ, 产生矛盾; 若u∼v2且u∼v3,则G[{u,v1,v2,v3}]H1,G[{u,v2,v3,v4}]H1, 并有(H1,σ)⊂Σ, 产生矛盾. 因此,u≁v4. 如果u≁v2且u≁v3,那么G[{u,v1,v2,v3,v4}]P5, 并且(P5,σ)⊂Σ, 产生矛盾; 如果u≁v2且u∼v3, 那么G[{u,v1,v2,v3}]C4, 并有(C4,σ)⊂Σ, 产生矛盾; 如果u∼v2且u≁v3, 那么G[{u,v1,v2,v3,v4}]H3, 并有(H3,σ)⊂Σ, 产生矛盾; 如果u∼v2且u∼v3, 那么G[{u,v1,v2,v3}]H1, 并有(H1,σ)⊂Σ, 产生矛盾. 故而dG(v1)=1. 类似可得dG(v4)=1.

断言10G[(N[v2]∪N[v3]){v1,v4}] 是符号完全图.

如果N(v2)={v1,v3} 并且N(v3)={v2,v4}, 那么结论显然成立. 如果|N(v2)|≥3 并且|N(v3)|=2, 那么存在另一顶点u使得u∼v2且u≁v3. 于是G[{u,v1,v2,v3,v4}]H2, 并有(H2,σ)⊂Σ, 产生矛盾. |N(v2)|=2且|N(v3)| ≥3 的情形是类似的. 接下来, 假设|N(v2)| ≥3 且|N(v3)| ≥3, 任取顶点u∈N(v2){v1,v3} 及w∈N(v3){v2,v4}. 若u=w, 则结论自然成立. 假设u/=w, 则断言u∼v3且w∼v2. 否则, 若u≁v3或w≁v2, 则G[{u,v1,v2,v3,v4}]H2或G[{w,v1,v2,v3,v4}]H2, 并有(H2,σ) ⊂Σ, 产生矛盾. 若u≁w, 则G[{u,w,v2,v3}]H1, 并有(H1,σ)⊂Σ, 产生矛盾. 于是u∼w, 结论成立.

令T=V(Σ)(N[v2]∪N[v3]),S=(N(v2)∪N(v3)){v1,v4}. 如果T=∅, 那么结论成立. 假设T/=∅, 则以下断言成立.

断言11|T|≤|S|.

设u∈T, 首先断言|NS(u)| ≥1. 否则, 存在顶点w∈T使得w与S中的任意顶点不相邻. 因此w与v1或v4的距离至少为4, 产生矛盾. 其次断言|NS(u)|=1. 否则, 存在顶点w∈T使得u1∼w,u2∼w, 其中u1,u2∈S, 因此由断言10,u1∼u2. 注意到, 根据断言10,G[{u1,u2,v2}]K3且G[{u1,u2,v3}]K3. 从而G[{w,u1,u2,v2}]H1,G[{w,u1,u2,v3}]H1, 并有(H1,σ)⊂Σ, 产生矛盾. 最后可断言NS(u1)∩NS(u2)=∅, 其中{u1,u2}⊂T. 否则, 存在一顶点w∈S使得u1∼w且u2∼w, 其中u1,u2∈T. 根据断言10,w∼v2且w∼v3. 如果u1∼u2,那么G[{u1,u2,w,v1,v2}]∼=H3且G[{u1,u2,w,v3,v4}]H3,并有(H3,σ)⊂Σ, 产生矛盾. 如果u1≁u2,那么G[{u1,u2,w,v1,v2}]H2且G[{u1,u2,w,v3,v4}]H2, 并有(H2,σ)⊂Σ, 同样产生矛盾.

断言12T是独立集.

如果|T|=|S|=1, 那么结论是平凡的. 假设|S|≥|T|≥2, 并设u1,u2∈T,w1,w2∈S使得u1u2,u1w1,u2w2∈E(Σ), 那么G[{u1,u2,w1,w2}]C4, 并有(C4,σ)⊂Σ, 产生矛盾.

结合断言9∼12, 如果diam(G)=3, 那么Σ 是平衡的其中2 ≤t≤s且s+t=n.

综上所述, 定理1 得证.

3 结论

对于n≥2 阶连通符号图Σ, 当时,本文得到了Σ 是平衡的(Kn,σ) 或者是平衡的或者是平衡的其中2 ≤t≤s,s+t=n,并且k≥2. 在将来的研究中, 可以探讨关于第二大符号距离特征值界的问题.