基于小波改进阈值的封隔器解封信号处理分析∗

丁韬，姜宏†，王海峰

(1. 新疆大学机械工程学院，新疆乌鲁木齐 830017；2. 红都有限责任公司，新疆克拉玛依 834000)

0 引言

封隔器主要用于实现隔绝产层或施工目的层的需求，防止层间流体压力相互干扰，影响措施作业的效果．封隔器是油田生产中不可或缺的井下工具，在采油、注水、目的层改造等作业环节都扮演着重要角色[1-3]．但在实际使用过程中，抽油杆往复运动以及数千米的管柱伸长或缩短所造成的冲击与振动可能会使工具锚定机构下移甚至滑脱、中途解封[4]，进而导致密封失效，严重影响生产效率．针对锚定机构卡瓦与套管咬合问题，韩传军等[5]利用有限元仿真对卡瓦结构参数进行了优化；张宏伟等[6]建立了锚定机构有限元分析模型，得出卡瓦与套管咬合深度随压力的变化规律；但目前尚未有通过封隔器锚定机构振动信号对封隔器在井下是否发生中途解封进行判断．

考虑到井下工况复杂，振源较多[7-8]，振动信号受噪声干扰严重，必须对其进行降噪处理，才能判别出封隔器是否发生中途解封的问题．针对噪声干扰问题，小波阈值降噪具有良好的时频局部化分析能力和多分辨率特性，在工程领域应用广泛[9-11]．但小波阈值降噪法对噪声非均匀分布的信号降噪效果较差[12]，并且软、硬阈值函数均存在不同缺陷[13-15]．针对软、硬阈值缺陷，周西峰等[16]提出渐近半软阈值函数方法，解决了硬阈值函数不连续问题，未解决软阈值函数的缺点．李红延等[17]提出一种改进阈值函数，可以通过调节参数改善软、硬阈值缺陷，但其参数过多，最优参数选取较为困难．针对噪声非均匀分布的信号，奇异值分解具有良好的代数和几何不变性[18]，可以将其正交分解为噪声分布相对均匀的分量，再对分解后的各分量进行降噪处理．虽然奇异值分解法对噪声非均匀分布信号降噪效果较好，但对冲击信号降噪效果较差[19-20]．

综合上述研究，本文首先通过有限元仿真得到封隔器正常及异常解封过程振动信号，其次针对小波阈值以及奇异值分解降噪方法的不足，在对阈值函数进行改进的基础上，提出一种改进阈值奇异值小波降噪方法，此方法有效解决了两种算法的局限性，改善了小波软、硬阈值函数的固有缺陷．最后通过本文所提方法对封隔器锚定机构振动信号进行降噪处理，并对降噪后信号进行分析，实现封隔器不同解封过程的判断．

1 Y211封隔器工作原理

压缩式单向卡瓦提放管柱坐封解封式封隔器（Y211封隔器）的结构如图1所示．主要由上下接头、胶筒、上下压帽、锥体、中心管、连接套、卡瓦、箍环以及卡瓦架组成．Y211封隔器坐封时，首先上提并顺时针转动油管使轨道销钉换向，上提旋转过程中依靠扶正器与套管壁之间的摩擦使得封隔器与套管保持相对静止，当卡瓦转入预定轨道后，此时增加压载，在外力作用下锥体下行撑开卡瓦，使得卡瓦张开嵌入套管内壁完成咬合，此时锚定机构与套管形成锚定进而使封隔器固定，继续增加载荷，上接头下行压缩胶筒，使得胶筒产生径向变形直至完全压缩，进而完成环空处密封．解封时，上提油管，上接头和中心管一起上行，中心管带动胶筒及锥体上移，胶筒在回弹力作用下恢复原状，上提过程中锥体上行脱离卡瓦，卡瓦在弹簧作用下恢复原位，此时卡瓦与套管的锚定解除，继而封隔器整体上提出井口完成解封动作．

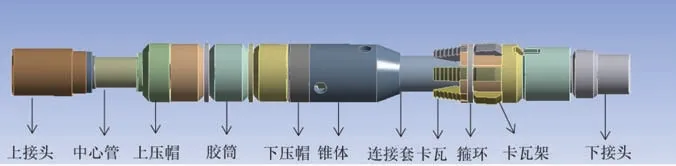
图1 封隔器结构示意图

2 封隔器有限元模型建立分析

2.1 有限元模型建立及简化

为研究封隔器不同解封过程中振动信号的变化趋势，首先根据Y211封隔器的结构特点、尺寸及工作原理，使用Unigraphics NX（UG）对封隔器各部件进行建模，将各部件进行装配得到Y211封隔器全尺寸三维模型．其次在中心管内增添抽油杆装置，通过抽油杆与中心管间的移动副模拟实际工作过程中抽油杆往复运动形成交变载荷，得到封隔器异常解封三维模型．之后将两种模型转化为Parasolid格式文件，并分别导入ADAMS软件中．

密封机构是封隔器正常工作的核心，但决定其是否能够良好密封的前提是锚定机构是否正常锚定．因此本文通过研究锚定机构振动信号进而判定解封状态，首先将上接头、下接头、上压帽、下压帽、胶筒等对仿真结果没有影响的部件进行简化；其次仿真分析时为了降低计算复杂度，将卡瓦架等部件的螺栓及销钉进行简化；最后对焊接和螺纹连接等连接方式进行简化，考虑到螺纹连接区域的机械结构、受力后应力-应变分布比较复杂，且对本文所要提取的封隔器锚定机构振动信号没有影响，故将封隔器所有螺纹连接部位简化为固定连接，最终得到简化后的Y211封隔器有限元仿真模型（图2）．对锥体、连接套和卡瓦架添加移动副，对套管添加固定副，并将施加在上接头的载荷施加在锥体上部．各部件材料均为钢材，接触处的摩擦系数均设定为0.15．

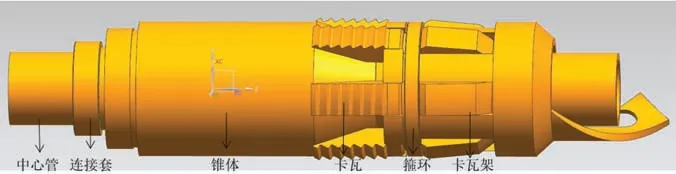
图2 封隔器三维仿真模型

2.2 各零部件材料选取

仿真模型简化后，根据实际生产及现场使用过程中具体情况对各零部件材料及性能参数进行选取．套管和中心管为重要的采油及承力部件，选用N80石油钢管；锥体由于要承受力的碰撞冲击，材料选用合金结构钢35CrMo；箍环和连接套等受力较小的零部件选用45号钢；卡瓦及卡瓦架选用20CrMnTi制成的渗透钢；所选各材料性能参数如表1所示．

表1 各零部件性能参数

2.3 仿真结果分析

由于Y211封隔器锚定机构为完全对称的规则回转体，仿真获得的锚定机构X和Y方向两组振动信号特征相似，故选取锚定机构X方向振动响应进行研究分析（图3）．

图3 不同解封过程锚定机构振动曲线

图3（a）为Y211封隔器完成密封工作后，正常上提解封过程的箍环振动曲线，0∼6 s为缓慢上提油管的过程，油管与上接头相连带动中心管上移，6∼14 s为锥体上行脱离卡瓦过程，由于卡瓦与卡瓦架之间有6组弹簧，卡瓦在弹簧作用下恢复原位，此时箍环振动位移幅值最大，达到0.22 mm；14∼20 s为上提过程，此时卡瓦逐渐恢复原位，对应的箍环振动位移幅值减小，但由于卡瓦与卡瓦架之间弹簧的存在，整个上提过程中箍环振动位移逐渐衰减，但未趋于0；

图3（b）为交变载荷影响下封隔器中途异常解封过程，0∼7 s对应抽油杆往复运动碰撞中心管的过程，锚定机构受到交变载荷作用，但由于锥体始终保持撑开卡瓦的状态，此时箍环振动位移曲线具体表现为较小幅度的密集振动；7∼12 s对应锚定机构蠕动过程，由于抽油杆往复运动碰撞中心管导致的卡瓦与套管咬合不紧，造成封隔器锚定机构下移，使得卡瓦收缩，箍环产生较大振动位移，幅值最大为0.17 mm，但由于锥体与卡瓦未完全脱离，此时卡瓦为不完全收缩，故箍环振动位移幅值相较正常解封过程较小；12∼20 s对应锥体在油管配重作用下轻微下行继续完全撑开卡瓦过程，此时封隔器处于完全坐封状态，卡瓦被锥体完全撑开，因此箍环振动位移曲线表现为抽油杆往复碰撞中心管产生的较小幅度密集振动．

3 仿真信号降噪处理

3.1 封隔器井下工况噪声分析

由于井下工况较为复杂，封隔器在完成隔绝产层的工作时会受到各种噪声干扰．井下噪声主要来源如下：井下工具在下放过程中产生的摩擦碰撞、油套管振动以及井下液体中的湍流在井筒中流动产生的噪声．以上几种工况的干扰频率和幅度随机性较大，归结为随机噪声，噪声频谱表现为高斯白噪声特性．因此在上述仿真过程得到的仿真信号中添加均值为0、方差为1的随机高斯白噪声，图4为含噪声的封隔器正常解封及异常解封振动信号时域波形图，可以看出噪声已经淹没封隔器解封过程各阶段的振动波形，影响了后续对封隔器解封工况的判断，因此，需要对井下干扰噪声进行降噪处理才能对其进行诊断分析，便于通过振动信号波形特征判断封隔器不同的解封过程．

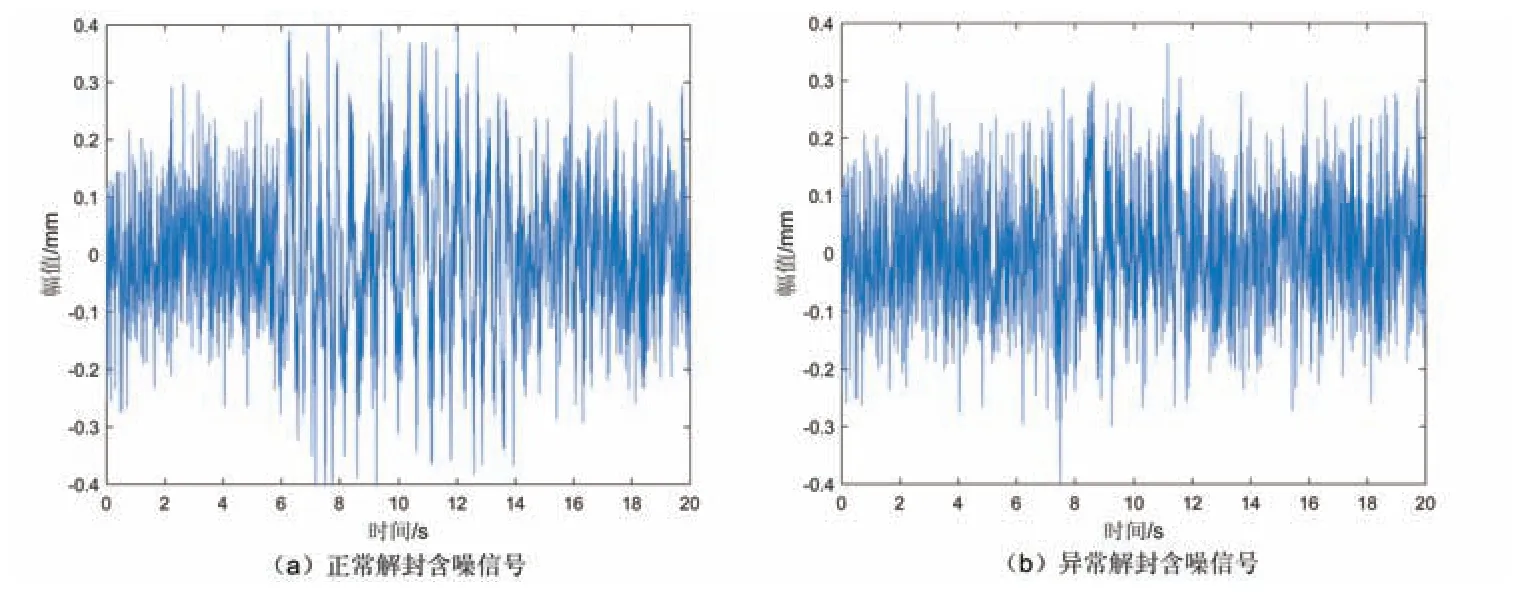
图4 含噪声的不同解封过程振动信号

3.2 改进小波阈值降噪法

假设封隔器解封过程含噪锚定机构振动信号表达式为：

式中：s(i)为含噪信号；f(i)为原始信号；e(i)为标准的高斯白噪声；σ为噪声方差；使用小波阈值法对信号s(i)中噪声进行去除，主要包括以下步骤：

1）确定适当的小波基及分解层数j，对信号进行j层小波分解；

2）选取合适的阈值对各层小波系数进行阈值量化处理，实际信号处理中常用的硬、软阈值函数表达式为：

3）根据底层尺度系数和量化处理后各层的小波系数，对信号进行小波重构．

由此可知，小波阈值降噪的核心在于选取合适的阈值及阈值函数．目前常用的软、硬阈值函数均存在不同缺陷．当j,k>λ时，软阈值函数处理后的小波系数与原小波系数之间始终存在固定偏差λ，会影响重构信号与原始信号之间逼近程度．硬阈值函数处理后小波系数在分段点±λ处不连续，利用该系数重构信号会产生振荡．针对软、硬阈值函数在降噪过程中的不同缺点，提出一种改进的阈值函数，表达式为：

式中：β> 1，取阈值为第j层分解的小波系数wj,k幅值的中间值．

图5为软阈值、硬阈值及改进阈值三种阈值函数曲线，通过函数曲线可以更直观反映出软阈值和硬阈值函数的固有缺陷．可以看出，改进阈值函数曲线在整个区间连续，无突变点，克服了硬阈值函数处理后的小波系数在分段点处不连续的缺陷；且通过指数函数的单调性，最大程度减小了处理后的小波系数与原小波系数之间的误差，解决了软阈值函数存在的缺陷；由于β∈[1,∞]，β值越大，两分段点之间曲线斜率越大，当β→∞时，此时该表达式趋近于硬阈值法；β值越小，两分段点之间曲线斜率越小，当β→1时，此时该表达式趋近于软阈值法；综上所述，改进阈值函数在保留了软、硬阈值函数优点的同时克服了二者各自存在的缺陷，且可以根据不同振动信号的特点调节β的值，使改进阈值函数与传统软、硬阈值函数之间可以灵活转化，是对小波阈值降噪方法的一次较好改进．

图5 小波阈值函数曲线

3.3 改进阈值奇异值小波降噪

将封隔器一维振动信号X=[x1,x2,···,xL]，转换为二维振动信号Hn×m．

将矩阵H进行奇异值分解得到H=α1H1+α2H2+···+αqHq+···+αrHr，将αqHq的各行首尾相连，可构造一维信号Sq={Sq1,Sq2,···,Sqa,···,Sqr}，Sqa代表矩阵Hq的第a行向量，故封隔器箍环振动信号可分解为X=S1+S2+···+Sr；

将小波改进阈值降噪与奇异值分解的方法结合，对封隔器锚定机构振动信号进行降噪处理，主要步骤如下：

1）通过奇异值分解将噪声非均匀分布的封隔器箍环振动信号分解为不同正交分量的叠加X=S1+S2+···+Sq+···+Sr；

2）利用改进小波阈值降噪法对步骤1）得到的各正交分量进行降噪；

3）将步骤2）所得各分量线性叠加，得到X′=

改进阈值奇异值小波降噪法对封隔器锚定机构振动信号降噪处理流程如图6所示．

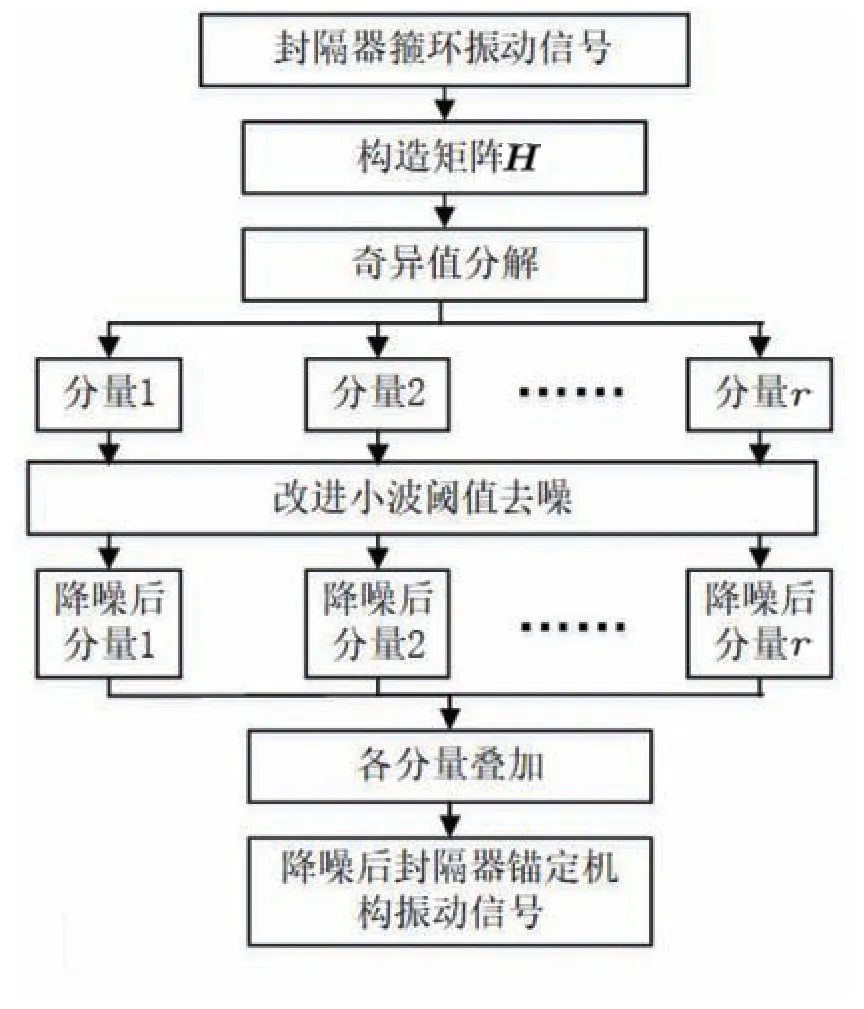
图6 改进阈值奇异值小波降噪法流程

3.4 仿真信号处理结果

对封隔器正常解封以及交变载荷影响下异常解封两种过程仿真信号分别用上述四种算法进行降噪处理，以消除噪声对波形的干扰进而更准确地判断封隔器工作状态．由于Symlets小波基具有良好的正交性及对称性，其阈值处理后的重构信号与原始信号更接近，目前在工程领域被广泛应用，其中sym4基函数的波形曲线与本文仿真信号波形相似，能够对噪声进行更好的去除，故选取sym4作为本文四种降噪算法的基函数．小波分解层数取3层，选用固定阈值，软阈值法和硬阈值法取阈值改进阈值和奇异值改进阈值方法取阈值求δ时四种方法均选用第一层小波系数中间值，奇异值分解将信号分解为256个正交分量．两组仿真信号降噪结果分别如图7及图8所示．

图7 正常解封锚定机构振动信号各方法降噪效果

图8 异常解封锚定机构振动信号各方法降噪效果

图7及图8（c∼f）分别为上述四种方法对两组振动信号降噪后的结果，从降噪效果图可以看出，硬阈值函数降噪后的信号波形仍存在毛刺，软阈值函数降噪后局部振动波形过于平滑，未能完全保留振动信号的原始突变特征．而奇异值分解加改进阈值降噪后的曲线在消除井下噪声干扰的同时较好地保留了锚定机构振动信号原始的波形特征，能明显区分出封隔器两种不同的解封过程，为封隔器振动信号的进一步分析提供数据支撑．

对于图7所示降噪后的时域图，曲线最大幅值达到0.22 mm，同时15∼20 s曲线呈衰减趋势，但并不趋于0，因此可以判断为正常解封过程；对于图8降噪后的时域图，曲线最大幅值0.17 mm，同时在12∼20 s曲线逐渐趋于0，可以判断为交变载荷导致的中途异常解封．

为更加直观反映各类阈值函数降噪性能的优劣，将信噪比（Rsn）与均方根误差（RMSE）两个参数作为降噪效果评级指标；其中，Rsn越大，RMSE越小，表明降噪效果越好．

设原始信号为x(n)、降噪后的信号为x′(n)，则信噪比定义为：

原始信号和降噪后信号的均方根误差定义为：

由表2可知，针对添加随机高斯白噪声的正常解封振动信号，本文所提出的奇异值改进小波阈值法及其它三种算法均取得了较好的降噪效果．相较软阈值、硬阈值、改进阈值三种算法，本文所提算法信噪比分别高出0.835 9、1.049 3、0.192 2 dB，均方根误差分别降低0.001 6、0.002 0、0.000 4；证明本文所提算法对噪声分离和去除效果更佳．

表2 正常解封信号降噪效果评价

由表3可知，利用小波改进阈值对交变载荷影响下异常解封箍环振动信号进行降噪处理，信噪比为13.060 5 dB，均方根误差为0.007 6，降噪效果优于小波软、硬阈值方法；而采用奇异值分解与小波改进阈值方法对异常解封信号进行降噪后，信噪比提升到13.503 4，均方根误差降低为0.007 1．两项降噪效果评价指标均得到改善．进一步说明针对两种工况下的封隔器锚定机构振动信号，改进的联合降噪法降噪效果明显优于现有的小波软、硬阈值去噪．能够更好地消除噪声对于判定封隔器工作状态的影响．

表3 异常解封信号降噪效果评价

4 结论

1）本文建立的有限元仿真模型模拟了封隔器正常及异常解封过程，所提取的振动信号能够区分两种工作状态，为封隔器工作状态检测提供了一种新方法．

2）本文所提算法优化了传统软、硬阈值函数的固有缺陷，相较小波软、硬阈值降噪，信噪比分别提升4.80%和8.02%，均方根误差分别降低7.79%及12.35%，降噪效果更好，具有良好的应用前景．