新型无耳托板螺母拉铆过程数值仿真与试验验证

王守财 孙昂 刘如刚

摘要：一种新型304不锈钢无耳托板螺母的安装效率较高且能减少疲劳源，在航空领域应用广泛。基于Johnson-Cook模型建立了有限元模型，对该螺母拉铆成形过程载荷变化趋势、塑性流动、夹紧力与干涉量、夹层状态对铆接质量的影响分别进行分析，并开展了螺母的铆接安装试验。结果表明：有限元仿真模型与试验载荷曲线符合性较好，最大载荷误差为2.4%；螺母在受压应力远高于材料屈服应力时才发生结构失稳，迅速形成褶皱，塑性流动主要沿径向发展；拉铆过程可以给夹层提供一定量的夹紧力与干涉量，夹紧力在完成铆接后达到最大值，且在一定范围内夹层的斜度不影响夹紧力的大小，铆接过程最大干涉量为4.6%左右。

关键词：304不锈钢；无耳托板螺母；Johnson-Cook模型；拉铆

中图分类号：V229

DOI：10.3969/j.issn.1004132X.2023.07.014

Numerical Simulation and Experimental Verification of Pulling-riveting

Process of New Non-plate Nuts

WANG Shoucai1 SUN Ang1 LIU Rugang2

1.Shenyang Aircraft Design & Research Institute，Aviation Industry Corporation of China，

Shenyang，110035

2.Xian Zhitong Aviation Technology Corporation，Xian，710000

Abstract： Due to the excellent characteristics in improving installation efficiency and reducing fatigue sources， a new type of 304 stainless steel non-plate nut was generalized in aviation field. Based on Johnson-Cook model， the finite element model was built to analyze the pulling-riveting progress. The loading-curve， plastic-flow， clamping force and interference amount， and the influences of interlayer state on riveting quality were analyzed. Meanwhile， the riveting installation tests of nuts were carried out. Results show that the finite element simulation model is in good agreement with the test loading curve， and the maximum load deviation from test is as 2.4%. When the compression stress of the nut is much higher than the yield stress of the material， the instability of the structure occurs， and the bulge structure is formed rapidly. The plastic flow mainly develops along the radial direction. The pulling-riveting process may provide a certain amount of clamping force and interference to interlayer. The clamping force reaches the maximum value after complete riveting， yet in a certain range， the slope of the riveting interlayer does not affect the clamping force. The maximum interference in the riveting processes is about 4.6%.

Key words： 304 stainless steel; non-plate nut; Johnson-Cook model; pulling-riveting

0 引言

作為“工业之米”，紧固件在航空领域有着极为重要的应用，主要用于飞机结构、成品附件的连接。目前一架军用战斗机中紧固件的用量可达50万件以上，大型运输机紧固件的用量更是达到200万件，紧固件的质量占飞机结构质量的5%左右。可以说，紧固件的使用遍布机身各个部位，正因为如此，其连接质量直接影响了飞机的安全与寿命。

螺母作为最常用的紧固件之一，与螺栓配合使用起到连接承载的作用，目前飞机上的应用以托板螺母（双耳、单耳、角型）、自锁螺母和高锁螺母为主。随着对飞机寿命指标的要求越来越高，飞机设计师在考虑减重的同时，也要尽可能地减少可能存在的疲劳源。传统的托板螺母需要在结构上钻铆钉孔，不仅增加了疲劳源，也严重影响了装配效率，本文研究的新型无耳托板螺母，通过拉铆的形式固定于结构上，不需要单独钻铆钉孔，减少结构疲劳源，提高了安装效率，同时便于结构中狭小部位的连接安装，另外，其独特的类椭圆头部结构起到螺栓拧入过程的防转作用。

由于新型无耳托板螺母的应用经验尚浅，对其成形机理、性能特点等尚不完全明晰，因此本文对新型无耳托板螺母铆接成形过程进行数值仿真，并开展试验验证，研究该产品在拉铆过程中的应力和塑性成形特点，为工程应用提供支持。

1 有限元模型的建立

1.1 无耳托板螺母产品结构

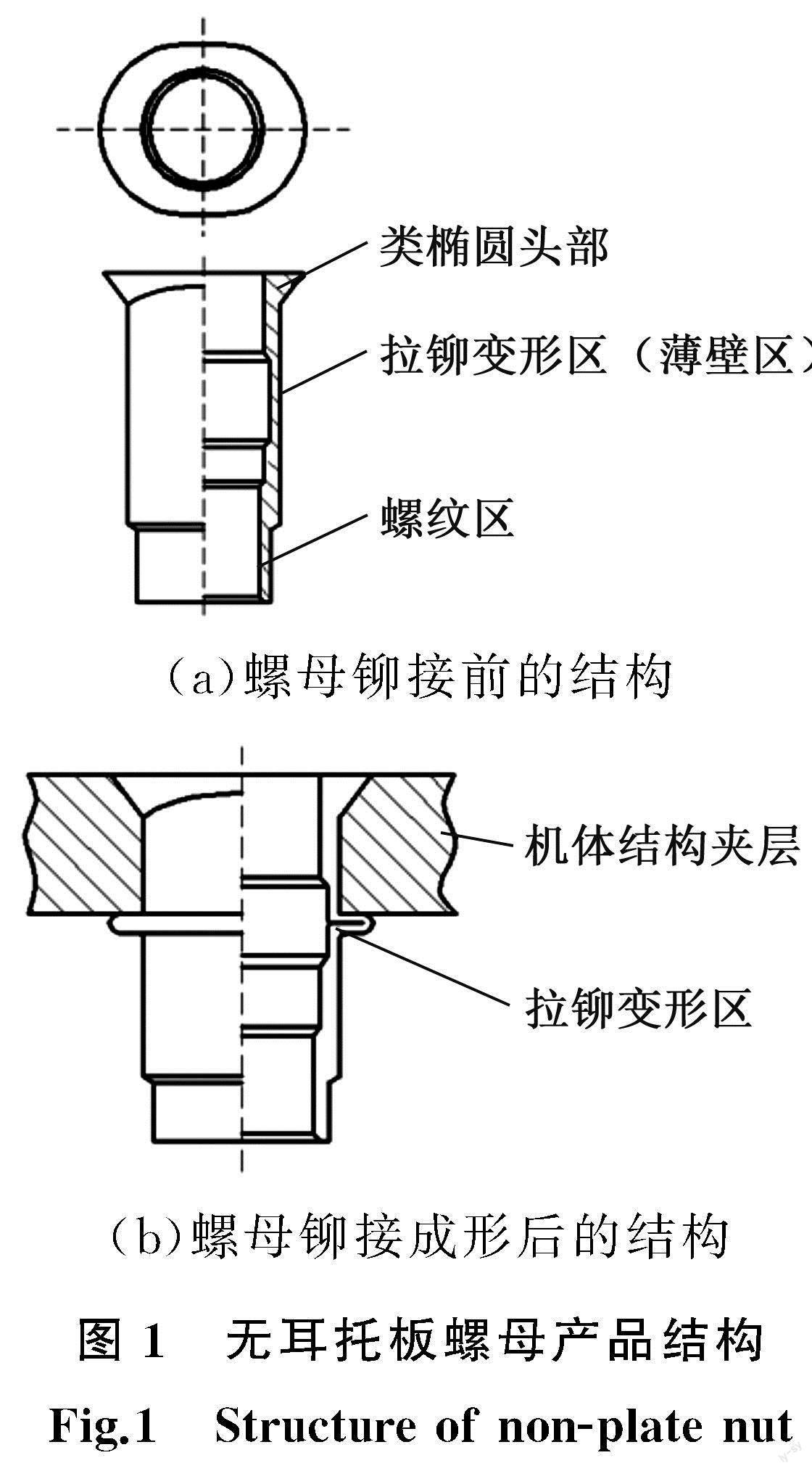
无耳托板螺母产品结构见图1a，材料为304不锈钢，安装前需要使用特制的工具完成椭圆沉头孔的划窝，螺母铆接变形区域较其他承载区域壁厚更薄，便于铆接成形，安装后示意图见图1b。

1.2 材料本构模型

根据Johnson-Cook本构模型［1］，有

文献［2-3］对不同应变率下金属材料的性能进行了研究，证实了304不锈钢以及拉铆变形过程中应变速率对数值仿真结果有较大影响。文献［4-6］经过大量试验，得到304不锈钢真实应力应变曲线（图2），并最终确定了Johnson-Cook模型参数（表1）。

本文模型与试验均在室温条件下进行，忽略环境温度影响，得到材料本构方程：

1.3 有限元模型

有限元模型见图3，模型由上下两个夹层、驱动螺栓、螺母共同组成。采用两个夹层进行铆接仿真的目的是便于计算无耳托板螺母铆接后对夹层的夹紧力。本模型不关注拉铆过程中驱动螺栓的受力情况，因此螺栓光杆部分设置为刚体，驱动螺栓与螺纹通过Tie约束绑定。铆接所用的上下夹层板材料为TC4，螺母为304不锈钢，材料弹性参数见表2［2，7］。螺母与夹层板网格采用八节点减缩积分单元（C3D8R），铆接中心区域网格加密。

模型边界条件设置：夹层板侧边固支，螺母头部平面限制轴向位移U1，驱动螺栓参考点限制除UR1外的五个自由度，并在铆接分析步中通过修改U1方向的位移进行加载。

2 试验验证

无耳托板螺母在飞机中的装配工具为专用铆枪，铆枪通过设定的载荷和拉伸行程，快速完成螺母的铆接成形，但却无法记录铆接载荷位移曲线。为了验证有限元模型计算结果的有效性，通过电子万能试验机进行同规格无耳托板螺母的铆接力测试试验，记录铆接过程中的载荷位移曲线，以及最大铆接力等。试验装夹方式见图4。

3 结果分析

3.1 仿真与试验结果对比

有限元仿真与拉铆试验载荷位移曲线见图5。

依据螺母在拉铆成形过程中的受力与变形特点，可以将整个过程分为三个阶段，见图6。

第一阶段为稳定承载阶段。驱动螺栓通过拉伸给螺母施加载荷，螺母实际变形部位受压，且随着加载位移的增大，载荷近似线性增大。螺母在该阶段处在弹性承力区，尚未发生塑性变形，整体受载迅速增大，变形较小，具体状态见图6a。

第二阶段为快速成形阶段。在第一阶段的基础上继续加载，螺母压应力率先到达非线性段，直接表现为载荷位移曲线斜率明显减小，经过较短的时间，载荷到达第一个峰值，

此时螺母薄壁结构处已经发生了失稳，该峰值也基本对应拉铆褶皱结构形成的开始，随后螺母迅速形成褶皱，该过程拉伸载荷有小幅减小，金属薄壁圆筒结构在受压失稳后载荷减小的现象在文献［8-10］的工作中也有相同的结论，受载具体状态见图6b。

第三阶段为最终成形阶段。该阶段为螺母铆接成形的末端，在此过程中，螺母失稳后形成的褶皱上下表面相互接触，铆接载荷略有升高，铆接过程完成，受载具体状态见图6c。

由图5结果可见，数值仿真结果能够较好地反映整个拉铆过程中载荷随加载位移的变化趋势，最终变形后状态也与试验状态相同（图7）。数值仿真结果最终成形阶段最大载荷为9017 N，与试验测量结果8804 N相比，结果误差仅为2.4%。

对铆接完成的螺母进行成形后直径以及成形厚度进行测量。由于螺母实际成形后的褶皱一般不是正圆，故测量时选取相正交的两个方向，取平均值，成形厚度测量时将螺母沿中线剖开进行放大测量，如图8所示。结果表明，有限元计算的成形后直径与厚度分别为8.46 mm与1.54 mm，试验测量结果分别为8.73 mm与1.38 mm，存在10%左右的误差。

3.2 螺母失稳分析

经过试验发现［11］，圆筒结构只有在变形区长度与圆筒半径比值在0.625～1.25之间时，才会在压缩载荷下稳定形成单个褶皱，更大量的计算与试验表明该范围为0.438～1.5［12］。上文已经提到，本文所用的无耳托板螺母通过驱动螺栓的拉伸进行铆接，但对于实际变形的薄壁区域（图1），其受载形式为压缩载荷，且该区域总长与螺母半径的比值为0.92，根据文献［11-12］的结论，在压缩载荷下螺母可以稳定形成单个褶皱。下面将对螺母在拉铆变形过程中的弹性变形与塑性流动行为进行分析。

对于本文算例，在弹性变形区，易得螺母受压过程中为单轴压缩状态，取柱坐标r、θ、z（其中柱坐标的z轴对应笛卡儿坐标系的x1方向），易得剪应力分量均为0，且σz＞σθ=σr=0，因此σr，σθ，σz即为主应力方向。此时产生的弹性应变大小为

式中，F为轴向载荷;E为材料弹性模量;A0为螺母薄壁结构的初始截面积。

采用von Mises准则［13］对螺母材料进入塑性区的屈服行为进行判定：

式中，τoct为最大剪切应力;J2为偏应力张量的不变量;k为材料常数，代表纯剪试验中的屈服应力。

该屈服准则也受中间主应力的影响，因此可写成

f（J2）=J2－k2（5）

或

（σ1－σ2）2+（σ2－σ3）2+（σ1－σ3）2=6k2（6）

其中，σ1、σ2、σ3分別代表在笛卡儿坐标系下的三

当σz＞σ0时，由式（6）可得，材料达到von Mises屈服条件，发生屈服，产生明显塑性应变，此时螺母非薄壁区域尚处于弹性区域，弹塑性区域的分界面为垂直于螺母中线且位于薄壁与厚壁交界区域的两个平面。根据流动法则：

式中，dλ是一个贯穿于整个塑性加载历史的非负标量函数；εpij为塑性应变矢量；f为塑性势能函数；f/σij规定了塑性应变增量矢量dεpij的方向。

可见，塑性应变沿着当前加载面的法向产生，因此螺母同一个屈服平面的材料沿径向向外流动，导致直接承载面积A1略小于初始截面积A0。根据式（2），进入塑性变形阶段后，有如下平衡方程成立：

为简化分析，暂且认为ε·在发生塑性变形、螺母失稳之前近似保持定值，则有

F∝（310+1000ε0.65）A1（9）

通过式（9）不难得出，在进入塑性变形之后，压缩载荷F随着等效塑性应变的增大而增大，但斜率逐渐减小，此时基本已经处在图5中的快速成形阶段初期，当螺母无法继续承受不断增大的压缩载荷时，结构产生失稳，螺母薄壁迅速坍缩成褶皱结构（图5的快速成形阶段）。

根据von Mises塑性流动准则，材料在σz=σ0时即发生屈服，开始产生塑性永久变形，但按照仿真结果，螺母结构在7828 N（试验结果为7361 N）时才发生失稳，彻底失去承载能力，此时薄壁结构对应的主应力σz为717 MPa，远超过材料的初始屈服应力，说明在材料达到屈服应力后仍具备一定的承受压应力的能力，无耳托板螺母拉铆成形属于典型的塑性失稳过程。

图10所示为沿厚度方向的6个节点对应的塑性应变分量。可见在加载的初始阶段，厚度方向所有的塑性应变均为0，当σz＞σ0后，产生塑性应变，在厚度方向，由于外壁对内壁材料塑性流动的阻碍作用，导致塑性应变曲线产生“分叉”。当继续加载至图中的失稳点时，内壁处节点应变率先产生拐点，由于螺母的迅速成形，各位置塑性应变剧烈变化，最后褶皱区内壁的塑性变形明显大于外壁的塑性变形，与图9中的结论一致。值得注意的是，褶皱区内壁在最后应变稳定的阶段是拉伸产生的塑性应变，而外壁仍承受一定的压缩载荷，节点3位于中性面附近，最后的塑性应变基本为0。

图11所示为螺母外壁沿加载方向的三个节点（见图9）的塑性应变情况，其中节点2位于变形最大区域。可以看出，在螺母发生失稳后，节点1和节点3塑性应变变化不明显，而位于变形最大区域的节点2，PE33应变分量迅速增大，表现为螺母沿径向迅速成形。

图10和图11中应变曲线在结构失稳后产生了锯齿状波动，推测是由于材料在塑性变形中产生了锯齿屈服的现象［14］。

3.3 螺母夹紧力与干涉量分析

对两个夹层接触节点的接触载荷求和，得到螺母铆接夹层之间产生的夹紧力见图12。由图可知，拉铆螺母对夹层的夹紧力在快速成形阶段逐渐增大，并在图中0.15 ms时达到最大值，此时间对应着螺母失稳后应变稳定的阶段（图10和图11），同时也是图5中载荷位移曲线中载荷最大点，此后，夹紧力随着驱动螺栓位移的增大逐渐减小。表明螺母对夹层的夹紧力主要为螺母失稳成形后褶皱对夹层板的压力，“过铆”并不会增大夹紧力，反而有可能使塑性变形区域产生损伤。

干涉连接（也称过盈连接）作为一种能够显著降低应力集中、提高连接结构强度和疲劳寿命的连接方法［15-17］，被广泛应用于航空结构的机械连接。但是，对于碳纤维复合材料结构，过大的干涉量会造成分层、脱胶等内部缺陷，反而会降低结构强度与疲劳寿命，因此对干涉量的精确控制是实现干涉连接技术的关键。干涉量的定义如下：

式中，I为干涉量；D为螺母成形后承载段直径；d为连接孔直径。

图13所示为铆接完成后螺母外壁对结构孔的干涉量，横坐标表示与螺母成形一侧的端面距离。数据显示无耳托板螺母铆接成形后对结构孔的干涉量最大可以达到4.6%，且干涉量最大的位置产生在与端面距离约2 mm（厚度共6 mm）的位置，其余位置干涉量为3%左右。

无耳托板螺母在飞机中的作用：螺母对夹层的夹紧力可以有效地防止螺栓安装过程中的转动与松脱，在高振动环境中可以起到很大的作用；而铆接成形后无耳托板螺母对结构孔壁的干涉可以起到增强结构疲劳性能、提升使用寿命的作用。但正是由于螺母铆接过程对孔的干涉挤压，当螺母安装产生不合格品，需要将原螺母破坏重新安装时，就必须换用规格更大的螺母，这也是目前航空无耳托板螺母应用的弊端之一，不过通过对安装工艺以及设备的不断优化，目前安装成功率较高。

3.4 不同夹层铆接效果对比

上文中模型上下夹层厚度均为3 mm，而总厚度6 mm也是该规格的无耳托板螺母连接较为理想的夹层厚度。调整仿真模型夹层总厚度及螺母铆接成形一侧的斜度，得到不同夹层状态下螺母对夹层的夹紧力，如图14所示。

对比厚度为6 mm的平板和3°斜度的夹层可知，同样的铆接夹层厚度，其铆接成形一侧的斜度基本不影响对夹层的夹紧力（仅限3°以内）。计算也发现，该结论同样适用于铆接过程的最大载荷。但是随着夹层厚度的增大，螺母铆接夹紧力呈现减小的趋势，当厚度由6 mm增大为6.75 mm时，螺母对夹层的最大夹紧力减小至原来的1/3左右，这是因为随着厚度的增大，螺母可供拉铆变形的薄壁区大量进入夹层，塑性流动减弱，变形不充分，形成的褶皱面积也相应地变小。但夹层厚度减小、夹紧力增大的同时，螺母沿径向的变形明显增大，褶皱厚度变小（表3），可能会产生变形损伤，带来潜在的应用风险，因此需要根据使用部位的夹层厚度与应用工况等对螺母的规格进行合理选择。

4 结论

本文采用有限元数值仿真与试验验证方法对无耳托板螺母拉铆成形过程进行研究，分析了过程载荷位移曲线，螺母结构失稳机理等，得到如下结论：

（1）螺母拉铆数值仿真與试验载荷位移曲线符合性较好，相比于试验结果，仿真计算铆接最大载荷误差仅为2.4%。

（2）理论分析与有限元计算结果都表明，螺母在拉铆成形过程中塑性流动主要沿着垂直于加载方向的平面向外，且有限元计算显示螺母在717 MPa的压应力下发生失稳，远大于初始屈服应力σ0，螺母的失稳过程属于典型的塑性失稳。

（3）螺母拉铆成形会给夹层施加一定量的夹紧力，该载荷在完成铆接后即达到最大值，“过铆”并不会增大螺母对夹层的夹紧力，反而有塑性损伤的风险，铆接同时会给孔壁施加一定量的挤压干涉，最大干涉量约为4.6%。

（4）螺母成形一侧的夹层斜度发生变化，而螺母铆接安装点的厚度不变时，铆接过程中的最大载荷与铆接后螺母对夹层的夹紧力基本不变，但夹层厚度变大会直接导致夹紧力变小。

参考文献：

［1］ JOHNSON G R， COOK W H. A Constitutive Modeland Data for Metals Subjected to Large Strains， High Strain Rates and High Temperatures［J］. Engineering Fracture Mechanics， 1983， 21：541-548.

［2］ 刘秀， 金霞， 楼航飞， 等. 304不锈钢箔材在不同应变速率下的拉伸性能研究［J］. 材料科学与工艺， 2019， 27（5）：59-65.

LIU Xiu， JIN Xia， LOU Hangfei， et al. Studies on the Tensile Properties of 304 Stainless Steel Foil at Different Strain Rates［J］.Materials Science and Technology， 2019，27（5）：59-65.

［3］ 张帅， 赵琪， 王华. 考虑应变率差异的铆接仿真建模和实验研究［J］. 机械设计与制造， 2018（9）：197-200.

ZHANG Shuai， ZHAO Qi， WANG Hua. Study on Simulation Modeling and Experiment of Riveting Considering Strain Rate Difference［J］. Machinery Design & Manufacture， 2018（9）：197-200.

［4］ 熊江茗， 周杰， 王时龙，等. 基于Johnson-Cook模型的不锈钢管剪切数值模拟［J］. 中国机械工程， 2020， 31（15）：1877-1884.

XIONG Jiangming， ZHOU Jie， WANG Shilong， et al. Numerical Simulation of Stainless Steel Tube Shearing Based on Johnson-Cook Model［J］. China Mechanical Engineering， 2020， 31（15）：1877-1884.

［5］ LEE S， BARTHELAT F， HUTCHINSON J W， et al. Dynamic Failure of Metallic Pyramidal Truss Core Materials —Experiments and Modeling［J］. International Journal of Plasticity， 2006， 22（11）：2118-2145.

［6］ LAAKSO S， AGMELL M， STAHL J E. The Mystery of Missing Feed Force — the Effect of Friction Models， Flank Wear and Ploughing on Feed Force in Metal Cutting Simulations［J］. Journal of Manufacturing Processes， 2018， 33：268-277.

［7］ 邓云飞， 张永， 张伟岐，等. 断裂准则对TC4钛合金板抗卵形头弹冲击的影响［J］. 中国机械工程， 2019， 30（19）：2378-2384.

DENG Yunfei， ZHANG Yong， ZHANG Weiqi， et al. Effects of Fracture Criterionon TC４ Titanium Alloy Plates against Impacts of Ogival-nosed Projectiles［J］. China Mechanical Engineering， 2019， 30（19）：2378-2384.

［8］ 李翀， 鄂大辛， 佘彩凤. 5A03铝合金管轴向压缩失稳形式及影响因素分析［J］. 精密成形工程， 2014， 6（2）：36-40.

LI Chong， E Daxin， SHE Caifeng， Analysis on Instability Forms of 5A03 Aluminum Alloy Tube under Axial Compression and Its Influencing Factors［J］. Journal of Netshape Forming Engineering， 2014， 6（2）：36-40.

［9］ 郭英濤， 任文敏. 关于限制失稳的研究进展［J］. 力学进展， 2004， 34（1）：41-52.

GUO Yingtao， REN Wenmin. Some Advances in Confined Buckling［J］. Advances in Mechanics， 2004， 34（1）：41-52.

［10］ GUILLOWS R， LU G， GRZEBIETA R H. Quasi-static Axial Compression of Thin-walled Circular Aluminium Tubes［J］. International Journal of Mechanical Sciences， 2001， 43（9）：2103-2123.

［11］ ALVES L M， SILVA C M A ， MARTINS P A F， et al. End-to-end Joining of Tubes by Plastic Instability［J］. Journal of Materials Processing Technology， 2014， 214（9）：1954-1961.

［12］ 余海燕， 何泽珍. 基于塑性失稳的圆管对称压缩研究［J］. 鍛压技术， 2016， 41（9）：58-63.

YU Haiyan， HE Zezhen. Symmetry Compression Based on Plastic Instability of Circular Tubes［J］. Forging & Stamping Technology， 2016， 41（9）：58-63.

［13］ 陈惠发，萨里普 A F. 弹性与塑性力学［M］. 北京：中国建筑工业出版社， 2005.

CHEN W F， SALEEB A F. Elasticity and Plasticity［M］. Beijing：China Architecture & Building Press， 2005.

［14］ 李传强， 许道奎， 韩恩厚. 镁合金塑性变形过程中锯齿屈服现象的研究进展［J］. 中国材料进展， 2016， 35（11）：809-818.

LI Chuanqiang， XU Daokui， HAN Enhou. Research Progress on the Plastic Instability Phenomenon of Magnesium Alloys［J］. Materials China， 2016， 35（11）：809-818.

［15］ 左杨杰， 曹增强， 杨柳，等. 基于对称加载的均匀干涉配合铆接方法［J］. 航空学报， 2016，37（3）：1049-1059.

ZUO Yangjie， CAO Zengqiang， YANG Liu， et al. Interference-fit Evenness Riveting Method Based on Symmetrical Loading［J］. Acta Aeronautica et Astronautica Sinica， 2016，37（3）：1049-1059.

［16］ 程晖， 樊新田， 徐冠华，等. 航空复合材料结构精密干涉连接技术综述［J］. 航空学报， 2021， 42（10）：524876.

CHENG Hui， FAN Xintian， XU Guanhua， et al. State of the Art of Precise Interference-fit Techno-logy for Composite Structure in Aircraft［J］. Acta Aeronautica et Astronautica Sinica， 2021， 42（10）：524876.

［17］ 魏景超， 矫桂琼， 闫照明，等. 单面螺纹抽钉干涉配合复合材料连接件挤压强度研究［J］. 航空学报， 2013， 34（7）：1627-1635.

WEI Jingchao， JIAO Guiqiong， YAN Zhaoming， et al. Bearing Strength of Composite Joints Interference-fitted with Blind Bolts［J］. Acta Aeronautica et Astronautica Sinica， 2013，34（7）：1627-1635.