航空发动机转子在冲击载荷下的振动响应分析与试验

聂卫健, 卢 愈, 唐 广,3, 杨晓光, 王金舜,3, 陈亚农,3

(1. 北京航空航天大学 能源与动力工程学院,北京 102206; 2. 中国航发湖南动力机械研究所,湖南 株洲 412002;3. 中国航空发动机集团 航空发动机振动技术重点实验室,湖南 株洲 412002)

航空发动机转子是发动机动力推进系统的核心部件,其在大冲击载荷下振动特性直接决定发动机能否满足在特殊作战环境和起降落方式下的安全运行需求。抗冲击载荷试验是考核航空、航海等设备的重要试验项目,比如,针对整机抗冲击试验,姚念奎等[1-3]提出采用整机落震的试验方法开展,在国内首先开展整机落震试验研究,并取得一定成果;付超[4]和陈海龙等[5]系统研究了船用设备的抗冲击能力和冲击载荷下的振动响应;万强等[6]则开展某燃气轮机高压转子-涡轮抗冲击性能研究,进行了冲击响应计算和分析。国内针对航空发动机转子和挤压油膜阻尼器开展了很多研究,掌握了转子动力学建模、计算与试验技术[7-10]以及挤压油膜阻尼器的减振特性与理论研究方法[11-14],但针对带挤压油膜阻尼器的航空发动机转子在冲击载荷下的振动响应建模和试验研究刚刚起步,亟需开展系统的研究。

本文建立了带挤压油膜阻尼器航空发动机转子的振动响应有限元分析模型,将转子在受到冲击载荷瞬时的振动响应拆分为谐响应和冲击响应,开展了转子谐响应、冲击响应的建模计算分析,分析了在不同脉宽的冲击载荷下转子的瞬时振动响应,并在振动台上开展了相应试验研究,对比分析了有限元计算结果和试验结果,提出了冲击载荷下航空发动机转子振动响应分析和试验方法,为某航空发动机研制提供技术支持。

1 转子结构

如图1所示,转子主要由动力涡轮轴、两级动力涡轮盘等零部件组成,动力涡轮盘之间通过端齿实现连接。转子采用4支点0-3-1支承方式,其中,2号支点采用了挤压油膜阻尼器结构,如图2所示。

图1 转子结构示意图Fig.1 Structure diagram of the rotor

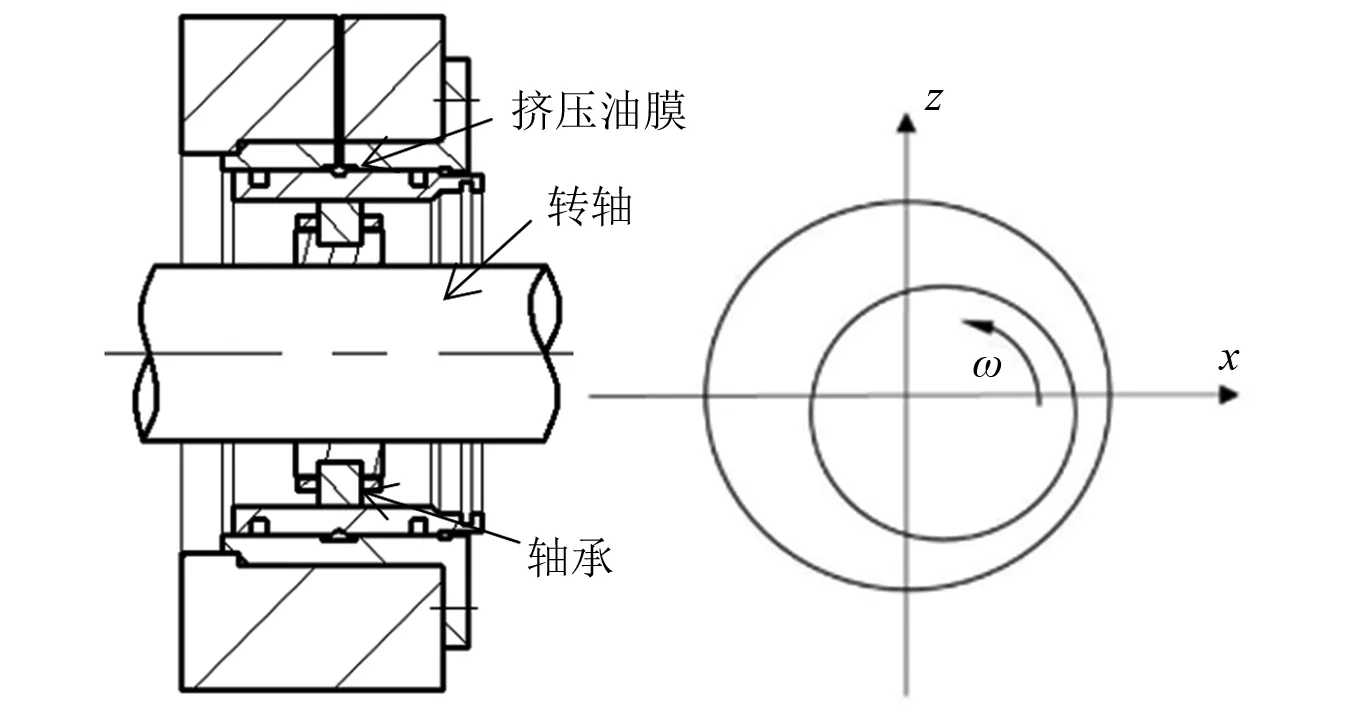
图2 挤压油膜阻尼器结构Fig.2 Squeeze film damper

2 谐响应建模及分析

2.1 有限元建模

采用ANSYS有限元软件基于梁单元建立转子的有限元模型,建模过程中,转子实体结构、支承、叶片质量和转动惯量分别采用梁单元、轴承单元、集中质量单元进行模拟。建立的有限元模型如图3所示,转子共3 641个节点。

图3 有限元模型Fig.3 Finite element model

2.2 谐响应分析

转子在运转过程中,振动响应主要包括受到不平衡力、支点支反力引起的响应,因此,不考虑转子的轴向运动,并考虑转子的陀螺力矩,转子的运动微分方程可写为

(1)

式中:M为惯性矩阵;G为陀螺矩阵;K为刚度矩阵;F1为不平衡激励力;F2为支点支反力;u为位移向量。转子有限元模型节点数为n,则M,G,K维度为4n×4n,F1,F2和u的维度为4n×1。在冲击瞬时,认为转子受到的不平衡激励力和支点支反力不变。

以N表示内部自由度、J表示界面物理自由度,采用固定界面模态综合法[15-16]对转子系统维数进行缩减(即按支承界面自由度和内部自由度对转子系统自由度进行分块,将物理空间转换为模态空间,缩减内部自由度,减小运动微分方程的数值求解计算量),建立转子系统的运动微分方程组,如式(2)所示

(2)

此外,支反力考虑了挤压油膜阻尼器的非线性油膜力,采用短轴承假设理论和Reynolds边界条件得到固定坐标系下的非线性油膜力为

式中:μ为滑油黏度;R为轴颈半径;L为SFD长度;c为油膜半径间隙;x,z分别为转子轴颈偏心在水平和垂直方向上的投影;I1,I2,I3为Sommerfeld积分;tanψ=x/y。

对于其他采用弹性支承的支点(1号、3号和4号),其支反力可表示为

(4)

式中,Kx,Kz分别为水平和垂直方向上的弹性支承刚度。

将式(3)、式(4)代入式(2),采用Newmark-β法对非线性微分方程组进行求解,再将求解结果通过矩阵运算由模态空间转换到物理空间,即可得到转子上的振动响应。

3 冲击响应建模及计算

为了得到转子在17 500 r/min转速下施加冲击载荷时转子的振动响应,建立了转子在旋转状态下施加冲击载荷时其振动响应的计算模型,如图4所示。为了充分模拟试验时转子、高速电机、支座、试验平台等安装的实际状态和振动台的冲击条件,同时为了建模的方便,将高速电机、支座、试验平台等用集中质量代替(见图4中“○”)。对整个模型同时施加转速和冲击载荷,施加冲击载荷时,分别施加如图5所示脉宽为6 ms和11 ms的的冲击载荷(冲击瞬时载荷大小为10g),为保证与试验时施加冲击载荷位置的一致性,冲击载荷施加在模型中间部位,然后计算得到转子轴上Z1,Z2,Z3处垂直方向的振动响应(分别用D1,D2,D3表示),分别如图6、图7所示。

图4 冲击响应计算模型Fig.4 Shock response calculation model

图5 不同脉宽的冲击载荷Fig.5 Impact load with different pulse width

图6 冲击响应计算结果(脉宽6 ms)Fig.6 Calculation result of shock response when pulse width is 6 ms

图7 冲击响应计算结果(脉宽11 ms)Fig.7 Calculation results of shock response when pulse width is 11 ms

4 冲击载荷下振动特性试验研究

4.1 试验设备

试验在如图8所示的振动台上进行,振动台主要由水平台面和垂直台面组成,具有施加半正弦波、三角波和锯齿波等冲击载荷的能力,振动台是根据电磁感应原理(即通以交变电流的线圈在恒定磁场中将受到交变力的作用)设计的振动发生装置,励磁线圈通入直流电后,在绕组中通过由功率放大器输入的交流驱动电流,动圈即在交变电磁力的作用下而产生运动,从而提供试验所需的冲击载荷。

图8 振动台结构示意图Fig.8 Structural diagram of the vibration table

4.2 试验安装与测试

按图9将转子安装在振动台上,试验采用高速电机驱动,通过变频器对高速电机启停、加减速进行控制。试验过程中测量转子轴垂直方向的挠度(见图9D1,D2,D3,测量位置与计算位置保持一致)、支座振动加速度、弹支应变、轴承温度等参数,限于篇幅,本文只针对转子振动响应进行分析。转子在振动台上安装实物照片如图10所示,试验前,预先开展了高速电机全转速范围内动力特性和抗冲击性能试验,验证了高速电机具备不低于10g的抗冲击能力;此外,还完成转子的全转速范围内的动力特性试验,确保了转子能够平稳越过临界转速、安全运行至17 500 r/min,为论文研究奠定了坚实的基础,限于篇幅,上述试验过程不再赘述。因试验冲击载荷大,转子转速高,试验风险较大,为确保试验安全,设计有安全防护装置,在振动台四周及上方采用双层10 mm厚钢板隔离防护,在防护罩内安装照明灯和摄像头,实现试验过程中对转子状态的远程监测,如图11所示。

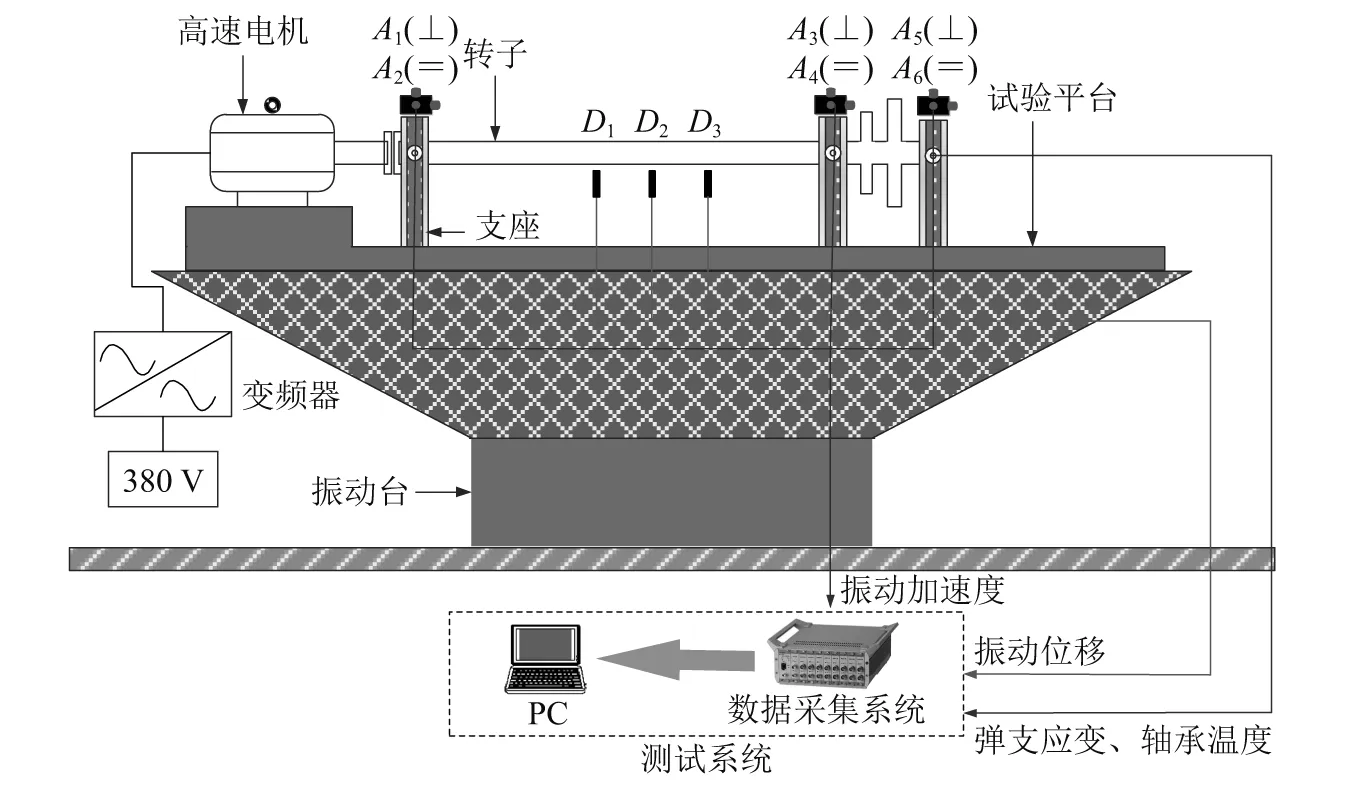
图9 转子测试安装示意图Fig.9 Test and installation schematic diagram of the rotor

图10 转子在振动台上的安装照片Fig.10 The photo of the rotor on vibration table

图11 远程监视画面Fig.11 Remote monitoring

4.3 试验结果

启动高速电机,带动转子运行至17 500 r/min的转速,随即启动冲击载荷控制系统,分别施加脉宽为6 ms和11 ms的冲击载荷(分别如图12、图13所示)。由3个位移传感器测得的冲击瞬时中的转子轴垂直方向的振动响应,通过读取冲击时间和对该时间段3个位移传感器测得的转子振动响应进行滤波处理,得到冲击瞬时振动响应时域信号,如图14、图15所示。

图12 冲击载荷谱(脉宽6 ms)Fig.12 Impact load spectrum when pulse width is 6 ms

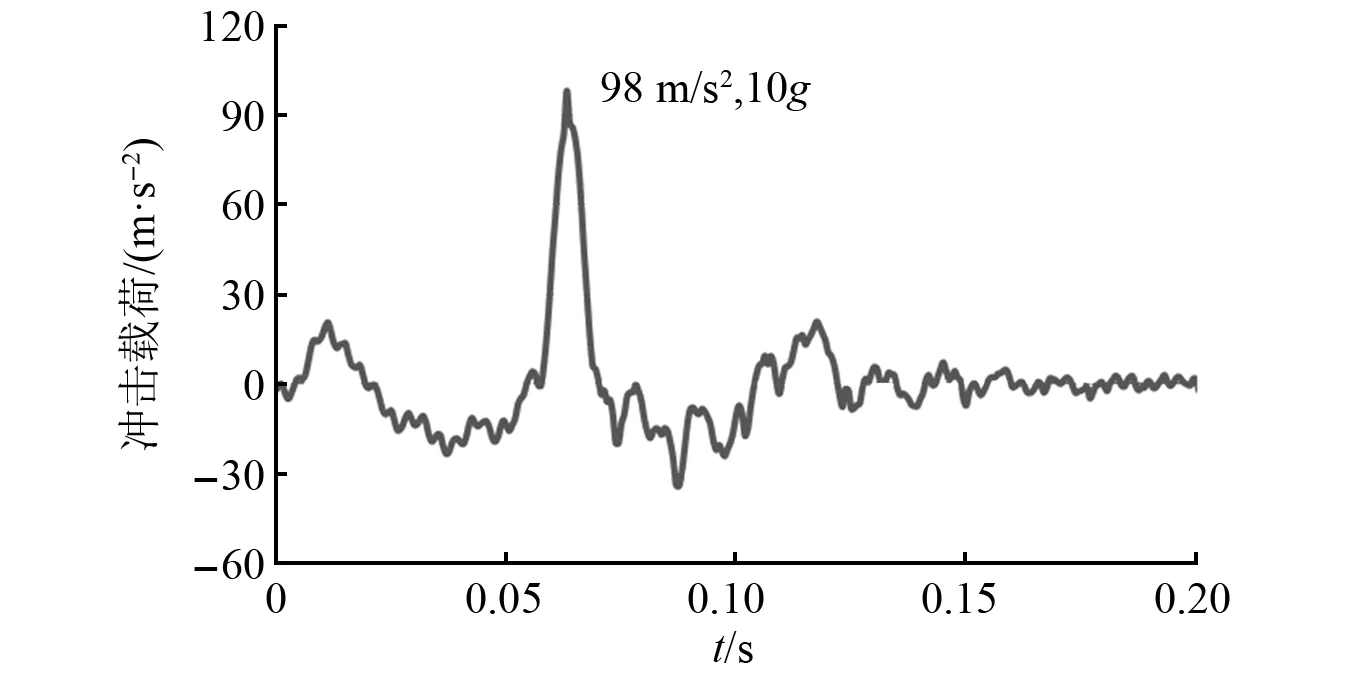
图13 冲击载荷谱(脉宽11 ms)Fig.13 Impact load spectrum when pulse width is 11 ms

图14 瞬态振动响应(脉宽6 ms)Fig.14 Vibration transient response when pulse width is 6 ms

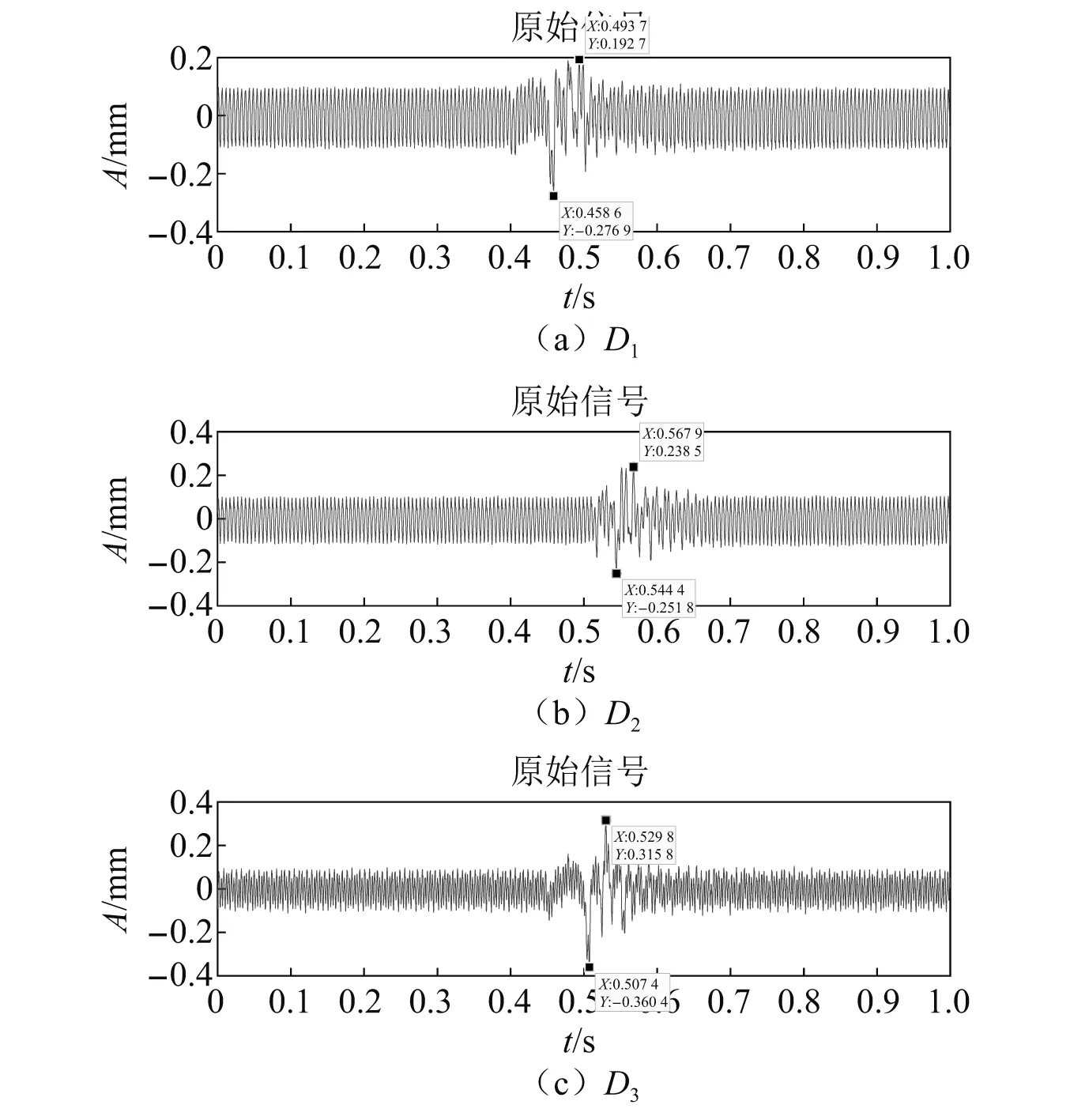
图15 瞬态振动响应(脉宽11 ms)Fig.15 Vibration transient response when pulse width is 11 ms

5 仿真分析与试验结果对比分析

通过读取试验振动响应结果,将计算结果与试验结果进行对比分析。定义计算误差的计算公式为

(5)

得到在不同脉宽的冲击载荷下,转子振动响应的计算误差,分别如表1和表2所示。表1、表2中,计算响应值为谐响应值(由第2章计算得到)和冲击响应值(由第3章计算得到)之和。

表2 计算值与试验值对比(脉宽11 ms)

由表1、表2可知,在一定脉宽范围内,不论是试验值还是计算值,冲击载荷的脉宽越大,各测点测得的振动响应值越小;计算响应值比试验响应值偏大,计算误差在10.44%～20.00%。

6 结 论

论文以航空发动机转子为研究对象开展冲击载荷下振动响应建模分析和试验研究,具有重要的工程应用价值。主要结论如下:

(1)冲击载荷大小一定时,在一定脉宽范围内,随着载荷脉宽变大,转子的振动响应变小。

(2)提出的试验方法顺利完成了转子在17 500 r/min转速下施加冲击载荷转子振动特性试验,获取了冲击瞬时转子振动响应,验证该试验方法的可行性。

(3)同一冲击载荷下,振动响应的计算值比试验值要偏大,计算误差在10.44%～20.00%,计算结果较好地反映了转子本身的振动响应,本文提出的建模方法可行。