基于逆向法的变轨距列车踏面优化设计
张 笑 池茂儒 谢雨辰 王欢声 蔡吴斌 代亮成
西南交通大学轨道交通运载系统全国重点实验室,成都,610031
0 引言
变轨距列车可以通过改变轮对内侧距的方式来匹配两种或多种轨距,实现跨国运输[1]。自变轨距列车的概念被提出以来,各国对此竞相展开研究,西班牙Talgo独立车轮变轨距转向架是最早的产品[2]。其后又产生了波兰SUW2000变轨距轮对[3]、德国DB AG/Ralif Type V变轨距轮对[4]、瑞士EV09变轨距转向架[5]、韩国KGCW轨距可调轮对[6]等具有代表性的产品。我国的变轨距列车相关研究起步较晚,黄运华等[7]提出了一种新型变轨距轮对结构;刘晓妍等[8]从车辆技术参数、线路以及车辆限界等方面对600/1067 mm变轨距转向架研发的可行性进行了分析。对于变轨距列车,轮轨关系是一个极为关键的问题,车轮匹配不同钢轨造成的轮轨关系差异直接影响到车辆在不同线路上的运行情况。石怀龙等[9]对变轨距高速列车的动力学进行了研究,发现影响变轨距转向架轮轨关系的主要因素为轨底坡和钢轨廓形,而非轮轨内侧距。QI等[10]对变轨距列车的LMB10踏面进行优化,优化后踏面匹配两种钢轨动力学性能均有所提高,但未考虑两种钢轨同时作用下的踏面磨耗性能。车轮廓形对车辆动力学性能和踏面磨耗性能有重大影响[11],由于变轨距列车需要匹配的钢轨廓形和轨底坡通常不同,故有必要进行踏面优化工作,以匹配多种类型钢轨。
车轮踏面逆向设计法是一种先给定踏面的接触关系曲线,再反推出踏面廓形的设计方法,目的性更强,踏面设计流程更短。LEARY等[12]从磨耗角度出发,采用钢轨型面扩展法设计车轮踏面。崔大宾等[13]提出了轮轨法向间隙法优化车轮踏面,可以减小轮轨应力。MARKINE 等[14]、SHEVTSOV[15]基于轮径差曲线进行车轮型面优化设计。POLACH[16]提出了基于等效锥度的车轮型面设计方法。SHEN等[17-18]提出了基于接触角曲线的踏面设计方法,以及基于轮径差和接触点在轨头偏移量的踏面外形逆向设计方法,该方法能够综合考虑动力学特性与轮轨匹配特性。IGNESTI等[19-20]基于磨耗模型,从降低磨耗的角度给出踏面设计方法。薛弼一等[21]引入侧滚角修正系数,解决了轮径差和接触点在轨头偏移量互相影响的问题。干锋等[22]基于轮轨初始接触点位置和轮径差曲线,结合参考踏面外形,提出了一种踏面反向优化设计方法。由于轮轨关系是十分复杂的,踏面逆向设计方法均是具有一定局限性的,存在设计变量多、优化模型迭代速度慢、难以拟合目标性能等问题[23],故需针对特定的设计需求,选择相应的设计方法。
本文对中俄变轨距列车匹配两种钢轨的轮轨接触关系和车辆系统动力学进行分析,提出匹配两种钢轨的踏面等效锥度设计方法,并应用逆向设计法对现有踏面进行优化设计,实现一种踏面与两种钢轨的均良匹配。
1 变轨距列车轮轨关系及动力学性能分析
分析变轨距列车的轮轨接触关系,主要考察接触点对分布、等效锥度和轨底坡带来的影响。对比踏面LMA与两种钢轨廓形(中国CHN60(文中60钢轨与CHN60钢轨同义)、俄罗斯P65)匹配的名义等效锥度λs。标准轨和宽轨线路上轮对内侧距分别为1353 mm和1440 mm,表1给出了不同轮轨匹配的名义等效锥度,其中,等效锥度计算方法采用UIC519标准[24]。

表1 高速踏面匹配不同钢轨的等效锥度
由表1可以看出,当轨底坡从1/40变为1/20时,LMA踏面与两种钢轨匹配的等效锥度均有一定下降,与P65匹配时下降到0.026,低于踏面等效锥度的允许使用下限,在实际运用中存在低锥度晃车风险。分析等效锥度下降的原因,图1给出了1/40轨底坡的CHN60钢轨和1/20轨底坡的P65钢轨廓形对比;图2给出了LMA踏面与两种钢轨匹配的接触点对分布情况。

图1 钢轨廓形对比Fig.1 Comparison of rail profiles

(a)LMA-P65 1/20轨底坡
对比图1、图2可知,P65钢轨1/20轨底坡工况下,廓形倾斜度更高,导致轮轨接触点集中在轨顶部分,LMA车轮廓形在此处为斜度1/40的直线段,故与P65钢轨匹配的等效锥度在0.025左右,存在低锥度晃车风险,同时易造成踏面凹磨。LMA与1/40轨底坡的60钢轨匹配时,轮轨接触点比较分散,名义等效锥度为0.04,具有较为优良的车辆动力学性能。
为进一步探究LMA踏面匹配不同钢轨廓形对车辆动力学性能的影响,根据我国某型高速动车组结构参数,利用SIMPACK多体动力学软件建立车辆系统动力学模型,如图3所示。

图3 动力学仿真计算模型Fig.3 Dynamic simulation calculation model
模型由1个车体、2个构架、4个变轨距轮对、8个轴箱等刚体组成,一系悬挂包括一系橡胶簧,二系悬挂包括空气弹簧、抗侧滚扭杆等部件,其中变轨距装置通过轮轴之间的销和花键实现。
车轮型面采用LMA踏面,钢轨廓形分别采用60和P65钢轨,采用武广高速线路实测轨道激励,对车辆在直线上的横向振动特性进行分析,计算得到车辆横向平稳性指标,如图4所示。

图4 LMA踏面匹配两种钢轨横向平稳性对比Fig.4 Comparison of lateralride index between LMA matching two types of rail profiles
由图4可知,车辆运行速度在100~300 km/h之间,LMA匹配P65钢轨的横向平稳性指标均高于匹配CHN60钢轨的横向平稳性指标。该指标在200 km/h的车速下达到顶峰。从200 km/h车速的时域信号来看,车体横向加速度方面LMA-P65显著大于LMA-CHN60。这种平稳性指标的变化规律较为符合低锥度晃车的规律。对该速度区间内LMA匹配两种钢轨的车体横向加速度频域进行分析,结果如图5所示。
由图5可知,LMA-P65的车体横向加速度幅值随车速的增加先上升后下降,其峰值发生在200 km/h时,与横向平稳性峰值位置一致;横向加速度主频随速度增大从0.528 Hz增长至1.111 Hz,与车体蛇行频率接近;车体横向加速度幅值方面LMA-CHN60显著小于LMA-P65,同时主频也与车体蛇行频率有所差异,所以可以判断LMA匹配P65钢轨时平稳性指标的升高是由于车辆发生了低锥度晃车[25-27]。
低锥度晃车问题还会影响车辆的蛇行稳定性,采用时域响应法[28-29]对车辆在两种钢轨线路上的临界速度进行计算,得到蛇行运动分岔图,如图6所示。

图6 LMA与两种钢轨匹配车辆稳定性对比Fig.6 Comparison of vehicle stability between LMA and two types of rail matching
当LMA与60钢轨匹配时,临界速度超过600 km/h;当与P65钢轨匹配时,车辆在150~300 km/h速度范围内出现由锥度过低引起的小幅失稳。车速大于450 km/h时一次蛇行与二次蛇行发生耦合,导致车辆临界速度降低至450 km/h。
对LMA匹配不同钢轨随里程的磨耗情况进行仿真分析,材料磨损模型采用常用的Archard磨耗模型[30]:
Vwear=kwNd/H
(1)
式中,Vwear为磨耗量;kw为摩擦因数;d为两接触物体相对滑移距离;N为法向力;H为相互接触的两个物体中较软的材料硬度。
轮轨法向力通过Hertz法确定[31],横向蠕滑力通过Fastsim算法求解[32]。式(1)中kw的取值与轨轮接触应力和滑移速度有关,其范围参考了JENDEL[33]的研究结果,如图7所示。为了便于计算,不同区域的摩擦因数用其中间值代替。

图7 摩擦因数取值范围Fig.7 The range of values for the coefficient of friction
由于实际运营过程中踏面和钢轨各位置硬度会随里程发生变化,摩擦因数也会随磨耗里程改变,故本文参考LI等[34]的研究,采用一种基于磨耗量的简化修正方法,以踏面廓形跟踪测试数据作为参考,在磨耗量计算公式中引入修正系数kc,定义为实测磨耗量与仿真磨耗量的比值:
kc=Δzr/Δzs
(2)
式中,Δzr为踏面磨耗量的真实值,可通过实测数据得到;Δzs为仿真计算的磨耗量。
由于kc的影响因素复杂多样,亦会随磨耗里程发生变化,故可以认为kc是关于磨耗里程s的非线性函数。图8所示为采用该方法对某动车组车轮磨耗计算得到的结果,仿真计算的磨耗量与实测结果重合度较高,证明该方法可以较好地预测实际运行过程中的踏面磨耗情况。
磨耗预测线路选取我国高速铁路代表性线路,设置三种轮轨匹配工况:CHN60、P65和两种钢轨均有的情况(为便于分析,两种钢轨线路长度比例为1∶3,速度级相同),在仿真过程中不断用磨耗后踏面替换初始踏面,研究踏面服役周期内的磨耗规律,LMA踏面与两种钢轨匹配的名义等效锥度随磨耗里程变化曲线如图9所示。

(a)与CHN60钢轨匹配等效锥度
由图9可以看出,LMA在三种线路条件下的磨耗踏面与60轨进行匹配时,名义等效锥度均随磨耗里程的增大而增长,其中LMA在60、P65两种钢轨混跑线路条件下15万公里后名义等效锥度稳定在0.15;LMA与P65钢轨的磨耗踏面与P65钢轨匹配时锥度随磨耗里程的增长而增大,另外两种线路条件下的磨耗踏面锥度随磨耗里程的增长反而降低,尤其在变轨距列车实际应用中,这种锥度继续降低的现象将严重影响服役周期内的动力学性能。
图10给出了不同线路条件下的踏面磨耗量。可知,LMA踏面上的磨耗量分布情况与LMA在不同钢轨上的接触区分布位置一致。LMA踏面在P65钢轨上的磨耗深度大于它在CHN60钢轨上的磨耗深度,磨耗带也更宽。然而,造成这种较宽磨损的现象一定程度上是因为LMA与P65钢轨匹配存在低锥度晃车现象,轮对横移量会更大。
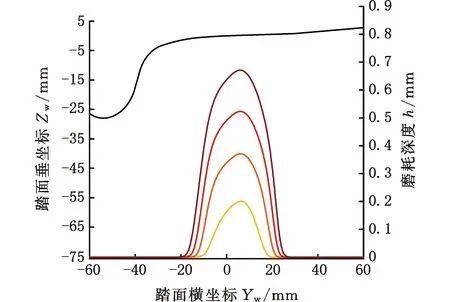
(a)CHN60钢轨条件下的踏面磨耗量
在两种钢轨共同作用下,踏面磨耗深度显著降低,磨耗带也保持在较宽的水平。磨耗量尖峰位置与踏面匹配两种钢轨的等效锥度相关,初始锥度0.04对0.026,踏面磨耗相对平均,当与P65匹配等效锥度下降后,磨耗带开始向LMA-CHN60的接触区转移。在磨耗过程中,LMA-P65的接触区处在磨耗带边缘位置,这一位置的廓形随着磨耗里程的增加将越来越平,导致LMA-P65的等效锥度随里程的增加而降低,而等效锥度降低又导致车辆低频晃动问题加剧,进一步增强这种“磨平”效应[35]。
磨耗预测和分析证明踏面与两种钢轨匹配时接触区的交错可以有效减小磨耗深度,同时磨耗量在踏面上分布的规律从磨耗性能角度为踏面优化设计提供了新的思路:应合理选择与不同钢轨匹配的等效锥度,调整磨耗量在踏面上的分布位置,优化磨耗性能。
对于上述问题,目前主要的解决方法包括踏面优化设计、悬挂参数优化等,踏面优化设计是从源头上解决这些问题的措施。反向设计方法不依赖设计师经验,设计过程较短,并且具有较高的精度,更适用于变轨距列车的踏面设计。因此,本文基于车轮型面逆向设计快速递推算法,提出匹配多种钢轨的轮轨关系设计方法,对LMA踏面进行优化,实现与CHN60、P65两种钢轨的均良匹配。
2 匹配不同钢轨的车轮踏面优化方法
目前车轮踏面设计方法主要有正向设计和逆向反推两种。正向设计法通过改变踏面廓形达到目标接触关系,这一过程需要大量调整和试凑,依赖设计者的经验;逆向反推法首先建立轮轨接触几何模型,通过输入等效锥度、接触角差、接触点分布等轮轨关系特性曲线,反推出踏面廓形,这类方法由于模型精确具体,故可以更快捷、准确地得到目标踏面。
匹配不同钢轨廓形的车轮型面均良化设计需同时关注它与不同钢轨的匹配关系,应用正向法优化时势必增加试凑过程,而采用逆向法,通过设计踏面与某一种钢轨的等效锥度来实现与两种钢轨的均良匹配,可以大大减小计算量,具有较高的准确度。因此,宜采用逆向设计法对LMA踏面进行匹配两种钢轨的优化设计。
2.1 车轮踏面逆向设计递推算法
车轮踏面逆向设计递推算法以等效锥度、接触点在钢轨上分布位置、钢轨廓形为输入条件,通过一系列几何关系逆推得到目标踏面廓形。
在踏面优化过程中,有初始踏面的接触关系作为参考,等效锥度改变的同时,可以同步改变接触点在钢轨上的分布曲线,快速确定接触点分布和等效锥度间的关系,从而简化设计流程,提高设计的准确度。接触点在钢轨上的分布曲线随等效锥度同步更改的方法如下。
首先建立铁道车辆轮轨动态接触关系几何模型,如图11所示。其中,s为轮对横移量,点A、B为左右轮轨接触点,RL和RR分别为左右轮接触点位置车轮半径,ΔL为接触点横向间距,2b为左右滚动圆间距,φ为侧滚角,δL和δR分别为左轮和右轮的接触角。
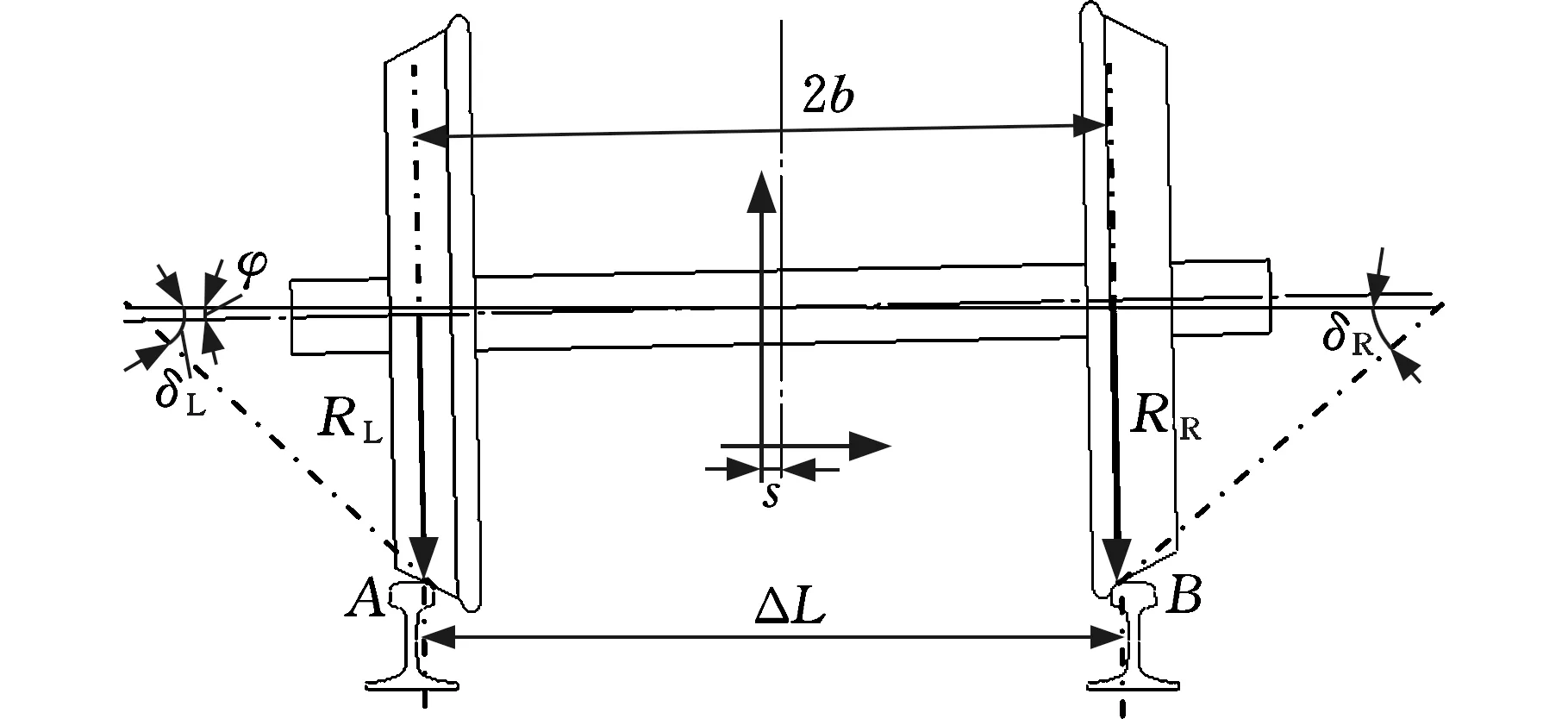
图11 轮轨几何接触关系示意图Fig.11 Schematic diagram of wheel rail geometric contact relationship
再确定接触点在钢轨上的分布带,即确定轮缘-钢轨接触点的位置和零横移时刻的轮轨接触点位置,如图12所示。其中,Yr(s)、Zr(s)分别为横移量为s时接触点在钢轨上的横、垂坐标,smax表示发生轮缘贴靠时的轮对横移量。为方便体现接触点在钢轨上的分布区域,将右侧轮缘与钢轨接触时左轮与钢轨接触点放在图12中的右侧钢轨上。

图12 轮轨接触点位置示意图Fig.12 Schematic diagram of wheel rail contact point position
踏面反向设计主要优化常接触区,在轮缘厚度、高度、轮对内侧距等参数不发生变化的情况下,优化后的踏面将继承原踏面的轮缘-钢轨接触位置坐标,即(Yr(smax),Zr(smax))、(Yr(-smax),Zr(-smax))可以确定。
轮轨接触原点坐标(Yr(0),Zr(0))决定零横移时刻的等效锥度。横移量非常小时,踏面和钢轨的接触可以近似为线性,同时轮对侧滚角φw(0)也近似为0,轮轨接触点位置的钢轨斜率和踏面斜率相等。通过将踏面斜率转换为轮径差ΔR(s)与横移量微增量Δs之间的关系,得到该点上钢轨廓形梯度的表达式:
(3)
同时,钢轨上每接触点位置的廓形梯度与接触角差曲线之间还满足下式:
gr[Yr(s)]-gr[Yr(-s)]=Δδ(s)
(4)
转换至初始轮轨接触位置:
gr[Yr(0+Δs)]-gr[Yr(0-Δs)]=Δδ(0+Δs)
(5)
轮轨接触点的疏密程度可以反映轮径差随横移量的增长速率,所以在逆向设计时,可以有根据地调整接触点分布情况以适应轮径差的变化。得到零横移时刻接触点坐标(Yr(0),Zr(0))和轮缘接触点坐标(Yr(smax),Zr(smax))后,通过建立轮径差增长率与接触点坐标增长率之间的映射关系,求出接触点在钢轨上的具体分布:
(6)
式中,ΔR(smax)为发生轮缘贴靠时的轮径差。
得到与轮径差相匹配的接触点在钢轨上的分布规律后,代入由钢轨接触点坐标(Yr(0),Zr(0))和(Yr(smax),Zr(smax))、(Yr(-smax),Zr(-smax))所组成的钢轨接触区内,即可得到与优化后的等效锥度曲线相匹配的接触点在钢轨上的坐标分布(Yr(s),Zr(s))。
将接触点的钢轨坐标转换成与之对应的踏面坐标:

(7)
式中,b0为名义滚动圆间距之半;r0为名义滚动圆半径;φw(s)为轮对侧滚角关于轮轨横移量的函数。
对于式(7)中侧滚角φw(s)的确定,可转换为车轮轴线和接触点连线的夹角与接触点连线和水平线夹角之差,如图13所示。

图13 轮对侧滚角简化模型Fig.13 Simplified model of wheelset roll angle
图13中,O1O2为该时刻的轮轴中心线,A、B分别为左右轮轨接触点,ΔL为左右接触点的横向距离,ΔH为左右接触点的高度差,L为左右接触点连线距离,侧滚角φw(s)由下式确定:
(8)
其中,ΔH(s)和ΔL(s)分别为轮对横移量s时两侧钢轨接触点的高度差和横向距离,其计算公式如下:
ΔH(s)=Zr[Yr(s)]-Zr[Yr(-s)]
(9)
ΔL(s)=Yr(s)-Yr(-s)
(10)
依据设计经验,式(7)中车轮型面垂坐标Zw[Yw(s)]和侧滚角φw(s)都是非常小的量,在实际运算中Zw[Yw(s)]sinφw(s)项极小,对结果的影响不足1%,因此,为提高计算效率并实现线性递推过程,便于后续逐步分析设计过程中各因素对设计结果的影响,实现快速循环算法,考虑将其舍弃,得到接触点的踏面横坐标Yw(s)的近似表达式:
(11)
联立式(8)、式(11),即可在已知接触点在钢轨上的分布Yr(s)和轮径差ΔR(s)的前提下求出接触点在车轮上的位置Yw(s)。在轮轨接触点处,车轮和钢轨线形的导数之间存在如下关系:
gr[Yr(s)]+φw(s)=gw[Yw(s)]
(12)
对钢轨廓形进行离散化处理,求得接触点位置的钢轨型面导数gr[Yr(s)],由式(12)得到接触点位置的车轮型面导数gw[Yw(s)],与接触点位置的车轮型面横坐标Yw(s)匹配,通过数值积分的方式求得轮轨接触区的车轮型面函数Zw[Yw(s)],再与非常接触区廓形进行拼接,在接头位置平滑过渡,得到完整的踏面廓形。
设计过程中的轮径差和等效锥度意义相近,可以根据下式进行转化:
(13)
式中,λ为线性等效锥度;yw为轮对横移量。
得到新踏面后计算轮轨接触关系,并与目标等效锥度进行比较,若某横移处实际等效锥度小于目标等效锥度,则说明该横移量下的轮轨匹配点对无法提供较大的等效锥度,应将该接触点位置向远离零时刻位置移动,反之亦然。对接触点坐标放缩微调后,继续代入上述求解过程,直至得到满足目标锥度要求的车轮踏面廓形。
2.2 匹配不同钢轨的等效锥度指标设计
兼顾多种钢轨的踏面等效锥度设计首先需关注踏面与不同钢轨匹配的接触位置。以LMA匹配60和P65钢轨为例,LMA匹配两种钢轨的常接触区如图14所示。可以看出,LMA与两钢轨匹配的常接触区位置不同,LMA与60轨匹配的接触区在踏面-22.1~14 mm区间,而LMA与P65的常接触区在踏面横坐标6.8~22.85 mm区间,两者常接触区位置不同,且在踏面横坐标6.8~14 mm区间存在交集。

图14 LMA匹配两种钢轨接触区对比Fig.14 Comparison of contact areas between LMA matching two types of steel rails
在对LMA进行匹配两种钢轨的均良化优化设计时,若只改变LMA与其中一种钢轨独有接触区段的廓形,对LMA与另一种钢轨的接触关系的影响不大;若改变LMA与两种钢轨接触区的交集部分廓形,则会影响到LMA与另一种钢轨的匹配关系。上文已经证明,轮轨接触区段的交错对踏面匹配不同钢轨的动力学性能和磨耗性能是有利的,合理安排接触区段交叉放置可以在一定程度上减轻踏面凹磨。若将LMA与P65钢轨的等效锥度提升过多,则LMA与P65的接触区将扩大,势必影响到LMA与CHN60的接触关系,使其锥度变大,同时接触区重合部分较多可能会加重凹磨程度。等效锥度的设计还需要考虑车辆悬挂参数的设定,并确保在实际应用中磨耗量分布更加均匀。车轮与两种钢轨匹配的等效锥度的差异不应过大。
综合考虑,将名义等效锥度提高至0.04,与LMA匹配60轨相当,便于悬挂参数设置,且可以尽可能不影响LMA-CHN60接触区段的廓形,保证现有的接触区域分布,保留接触区交错减轻凹磨的优势。以这一等效锥度曲线作为踏面逆向反求算法的输入条件,进行踏面优化,图15给出了调整前后的等效锥度曲线。
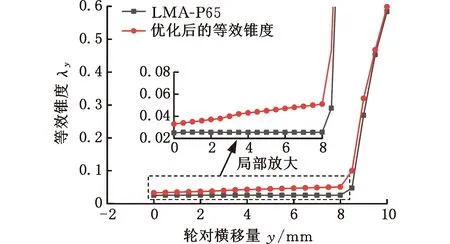
图15 等效锥度曲线调整Fig.15 Adjustment of equivalent conicity curve
3 优化车轮踏面及性能验证
3.1 优化设计结果
以上文给出的等效锥度、P65钢轨廓形为输入条件,通过踏面逆向递推算法,反求得到型面LMAopt,优化前后廓形对比如图16所示。可以看出,LMAopt与LMA相比,在横坐标0~30 mm区段廓形有明显变化,新型面在这一段内的斜度更大,与P65轨顶的共形程度更高,以实现匹配P65钢轨锥度整体提高的效果。同时横坐标小于0区段的廓形变化不大,有利于保持与CHN60钢轨匹配的等效锥度。
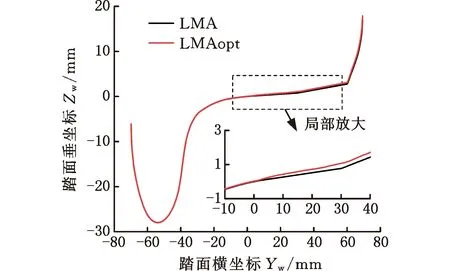
图16 优化前后踏面廓形对比Fig.16 Comparison of tread profile before and after optimization
图17给出了LMAopt匹配P65和60两种钢轨的等效锥度。可以看出,LMAopt匹配P65钢轨的等效锥度整体提高,名义等效锥度提高至0.041,与目标曲线吻合度较高,误差平均值为4.21%,相关系数超过0.99。同时LMAopt与60钢轨匹配时,等效锥度曲线基本与LMA相同,名义等效锥度保持在0.038。

(a)与P65钢轨匹配等效锥度
图18给出了优化前后踏面与两种钢轨匹配的接触点分布情况。由图可知,LMAopt与60轨匹配的接触区在踏面-21.9~12.5 mm区间,与P65的常接触区在踏面横坐标1.1~22.1 mm区间内,保留了与两种钢轨接触区段交错的现象,同时与P65钢轨接触带宽增大,有利于减轻车轮凹磨程度。

图18 优化后轮轨接触点位置Fig.18 Optimized wheel rail contact point position
3.2 动力学性能验证
图19给出了LMAopt和LMA型面匹配两种钢轨的横向平稳性对比,可以看出:与P65钢轨匹配,车速为100~150 km/h时,在平稳性指标方面LMAopt型面略低于LMA型面,在发生低锥度晃车的速度区间(车速175~250 km/h)内,LMAopt型面的平稳性指标显著更优,随着车速的继续增大,两型面平稳性处于同一水平。与60钢轨匹配时,在横向平稳性方面LMAopt型面略优于LMA型面。

图19 优化前后车辆横向平稳性对比Fig.19 Comparison of lateral ride index of vehicles before and after optimization
图20给出了LMAopt匹配P65钢轨的车体横向加速度频域,可以看出,与LMA相比,使用LMAopt-P65的加速度幅值显著降低,200 km/h车速下振幅最高可降低41.7%。此外,LMAopt型车轮的加速度主频也有所增加,避开了车辆不同速度下的蛇行频率,对低锥度晃车现象有明显的抑制作用。

图20 LMAopt匹配P65钢轨的车体横向加速度频域Fig.20 The frequency domain of the lateral acceleration of the carbody when the LMAopt profile is matched with P65 steel rail
图21给出了LMAopt和LMA踏面临界速度的对比。由图可知,当LMAopt与P65钢轨匹配时,车辆的蛇行失稳现象在150~300 km/h车速范围内得到有效抑制,临界速度也从450 km/h提高到550 km/h,提高了22%。当与60钢轨匹配时,LMAopt与LMA的临界速度基本相同,均可达到600 km/h,在与两种类型钢轨匹配时,LMAopt稳定性优于LMA踏面稳定性。

图21 优化前后车辆稳定性Fig.21 Vehicle stability before and after tread optimization
3.3 磨耗性能验证
利用上文的磨损预测模型对LMAopt型车轮轮廓的磨损性能进行分析,重点关注LMAopt踏面在两种钢轨共同作用下的磨耗性能[36],结果如图22所示。可以看出,在两种钢轨共同作用下,LMAopt踏面与CHN60钢轨匹配的名义等效锥度增长速度略高于LMA踏面。当LMAopt踏面与P65型钢轨匹配时,随着磨损里程的增加,锥度也会增加,20万公里时的等效锥度为0.24,避免了LMA踏面锥度随磨损里程的增加而降低的不利现象,有助于保持服役周期内的动力学性能。

图22 优化前后踏面等效锥度随磨耗里程变化Fig.22 The variation of equivalent taper with worn mileage before and after tread optimization
图23给出了LMAopt踏面上的磨损量随磨损里程的变化。在磨耗深度方面,LMAopt比LMA略深,20万公里时差异为0.058 mm,这种差异并不足以影响使用寿命和车轮镟修策略。LMAopt踏面的磨耗带从-15 mm到25 mm,比LMA踏面的磨耗带(-20~30 mm)略窄。这是由于LMA与P65钢轨匹配时等效锥度随着磨损里程的增加而降低,始终存在低锥度晃车的问题,这种现象最终导致了车轮磨耗宽度增加且磨耗深度降低[35]。换言之,LMA磨耗带宽的增加是以牺牲动力性能为代价的。图24中的车辆轮对横移量的对比验证了此结论。LMA的10万公里磨耗踏面与P65钢轨匹配时的轮对横移量明显大于LMAopt的10万公里磨耗踏面,动力学性能较差。因此,评估磨耗性能应考虑到服役周期内的动力学表现,在与LMA踏面对比时LMAopt踏面的磨耗性能具有显著优势。

图23 CHN60、P65混合条件下LMAopt踏面的磨耗量Fig.23 The wear amount of LMAopt under mixed conditions of CHN60 and P65 steel rails
4 结论
(1)本文建立了车辆系统动力学模型,用于分析在变轨距列车上使用LMA车轮踏面与CHN60型和P65型钢轨之间的轮轨关系和动力学性能。踏面匹配不同钢轨的等效锥度会影响磨耗分布,而多种钢轨对踏面不同接触区域的作用可以减轻踏面的凹磨严重程度。在变轨距列车中使用LMA的动力学性能和磨耗性能存在问题,因此,需要对踏面设计进行优化。
(2)对轮轨接触关系进行推导,简化车轮踏面逆向设计算法,使其更适用于对已有踏面进行优化。在此基础上,提出了一种考虑动力学性能和磨耗分布的匹配不同钢轨的踏面等效锥度的设计方法,给出了LMA匹配P65钢轨的目标等效锥度。
(3) 利用逆向设计法对LMA踏面进行了优化,得到优化踏面LMAopt。LMAopt与P65钢轨匹配的名义等效锥度为0.04,与60钢轨匹配的名义等效锥度为0.038;LMAopt与P65钢轨匹配时,能够有效抑制蛇行运动现象,临界速度提高了22%,并显著改善了横向平稳性指标;与60型钢轨匹配时,优化后踏面LMAopt的动力学性能与LMA处于同一水平。在两种钢轨的共同作用下,优化后的踏面廓形LMAopt的磨耗量和磨耗分布比LMA更合理,能够更好地保证车辆在服役周期内的动力学性能。

