面向多模式多元未知分布的协方差过程监控
赵 宇 李艳婷 吴振宇 周 笛 胡 洁
1.上海交通大学机械与动力工程学院,上海,200240 2.东华大学机械工程学院,上海,201620 3.上海通用五菱汽车股份有限公司,柳州,545007
0 引言
多元统计过程控制作为质量管理的重要工具之一,受到越来越多的重视[1-3]。过程监控能够很好地提前发现工业生产过程的隐藏风险,从而避免工业生产中因部件异常而导致的经济损失[4-6]。随着大数据时代的到来,越来越多的质量指标被记录下来,过程控制也向着多元化的方向发展。UEDA等[7]对多元控制图的发展进行了分类和总结。随着市场需求的发展,工业过程的多模式生产可以适应不同产品的制造过程以盈利[8]。同时,复杂产品的生产过程往往由多模式过程组成,这也导致过程数据呈现出多模式的特性[9]。因此,多模式过程监控受到越来越多的重视[10]。
多模式条件下的控制图大致可分为两类。一是为每个子模式构建单独的数据模型,并分别监视每个模式。MA等[11]基于局部邻域标准化(local neighborhood standardization, LNS)数据预处理算法,将数据缩放为单个数据,并提出了局部邻域标准化主成分分析(local neighborhood standardization and principal component analysis,LNS-PCA)的在线检测算法来解决多模式数据的故障检测问题。LYU等[12]提出了一种基于多模式过程学习的自适应监测方法,其中,模式识别和故障检测与自适应阈值策略相结合。LI等[13]针对工业过程中常见的多模式不确定性,提出了一种基于分层模式分割和子空间分解的多模式过程监控方法。郭金玉等[14]提出了基于概率密度和匹配系数的PCA多模式过程监测算法。CHEN等[15]提出了一种改进的即时学习(just-in-time learning,JITL)方法,用于自适应学习工业过程的多模式数据。CAO等[16]提出了一种使用方差贝叶斯主成分分析和Kullback-Leibler(KL)方差的多模式过程监测方法。
二是基于混合模型的在线监控方法,例如基于高斯混合模型(Gaussian mixture model, GMM)的多模式控制图[17]、基于隐马尔可夫模型(hidden Markov model,HMM)的控制图以及一些特定过程的模型控制图。SAMMAKNEJAD等[18]假设每个子模式服从多元高斯分布并基于期望最大化(expectation-maximum,EM)算法来训练整体GMM模型。JI等[19]基于变量之间的Mahanobis距离构建GMM混合模型,并监控GMM中所有高斯分量的后验概率。JIANG等[20]利用GMM模型和典型相关分析(canonical correlation analysis,CCA)来监控多模式过程。CHEN等[21]提出了一种基于时间约束的高斯混合模型方法,该方法可以通过考虑历史数据以及在线数据的模式识别中的时间序列信息来减少频繁模式转换过程的误报。CAO等[22]提出了一种基于高斯混合模型和贝叶斯主成分分析(Gaussian mixture model and Bayesian principal component analysis,GMM-VBPCA)的多模式在线监测方法,其中VBPCA用于为每个子模式建立概率模型。上述两类多模式控制图主要用于检测均值漂移,很少研究协方差矩阵的变化,且大多数现有的多模式控制图很少研究模式之间的过渡状态。
多元过程数据的可变性通常由数据的协方差矩阵表征。LI等[23]设计了一种基于协方差矩阵L2距离的协方差监测方案(LC控制图)。CAI等[24]针对观测数n小于变量数p的情况,设计了一种基于协方差矩阵L∞距离(CLX控制图)的监测方案。ZHU等[25]设计了基于稀疏主特征值检验的协方差监测方法(SLED控制图)。KIM等[26]提出了一种可以有效检测协方差变化的控制图,并且该控制图无需假设样本量小于变量的数量。ALFARO等[27]针对控制图检测能力不足的问题,在多元指数加权均方误差(multivariate exponentially weighted mean square error,MEWMS)控制图的基础上,提出了一种多变量加权协方差矩阵控制图(multivariate exponentially weighted covariance matrix combined control chart,MEWCMC)。NING等[28]针对具有测量误差的多变量质量监控问题,基于单个观测值场景的协方差矩阵绝对偏差的平方根之和,设计了一种新的控制图。EBADI等[29]系统总结了用于监测过程协方差的控制图并进行了分类。WANG等[30]提出了一种鲁棒性的非线性多模式过程监测方案,基于鲁棒核函数分解(robust decomposition of kernel function, RDKF)算法来检测异常值,将分块对角核函数矩阵与谱聚类相结合,设计了一种非线性模式识别方法。
目前关于多模式控制图的研究较少,且研究方法仍有很多不足之处。基于混合模型的检测方法要求数据服从一定的分布,这也限制了研究方法的通用性。同时,目前多模式控制图大多基于均值漂移模型的假设,在多模式条件下协方差检验控制图的研究报道较少。此外,上述多模式控制图对工业数据监控过程中普遍存在的过渡状态的研究甚少。
本文提出了一种针对多模式、高维和非正态数据的考虑模式过渡约束的协方差在线监测方法(multi-mode sparse principal eigenvalues exponentially weighted moving average control chart,MSPEWMA控制图)。首先使用基于交叉验证的线性收缩方法估计协方差矩阵;随后设计了稀疏主特征值检验统计量;之后考虑模式过渡约束的条件下构建了具有滑动窗口的指数加权移动平均(exponentially weighted moving average,EWMA)控制图——MSPEWMA控制图。MSPEWMA控制图采取模式过渡约束参数的策略,能够有效处理模式之间的过渡状态,并且对具有大漂移的多模式高维数据具有更好的监控效果。同时,MSPEWMA控制图适用于多种数据分布的监测,具有较好的通用性。
1 数据集介绍
风力发电机是典型的物联网设备,其数据由(supervisory control and data acquistition,SCADA)系统收集,通过本地服务器进行集成和处理,并通过互联网上传到云,以监控和评估运行状态。本文所采用的SCADA数据集为时间区间2019年1月1日至2019年12月31日的10 min采样间隔的全年风电数据,SCADA系统收集了风电运行过程中的温度、风速、功率、电流、电压等指标,包括齿轮箱冷却水温度、风轮转速、机舱温度、报警状态、发电机冷却水温度、瞬时风速、箱变油温、发电机定子U温度、有功功率、座舱温度、低速轴承温度、高速轴承温度等。图1是这些变量不满足正态性假设,某风场的某台风机四种变量的QQ plot图,可以看出,利用传统的控制图不能很好地对风机过程数据进行有效监控。图2是某风场的某台风机四种变量在连续一周时间的SCADA运行数据。该数据表现出多模式现象,风机的不同变量在各个运行模式下表现出不同的变化趋势。当自然风速达到一定阈值时,风力发电机转子才会旋转。同时,为了保护风机相关设备,风力发电机的最大输出功率受到限制(当自然风速超出一定阈值后,风轮转速不再持续增加,而是稳定在某一个阈值上)。
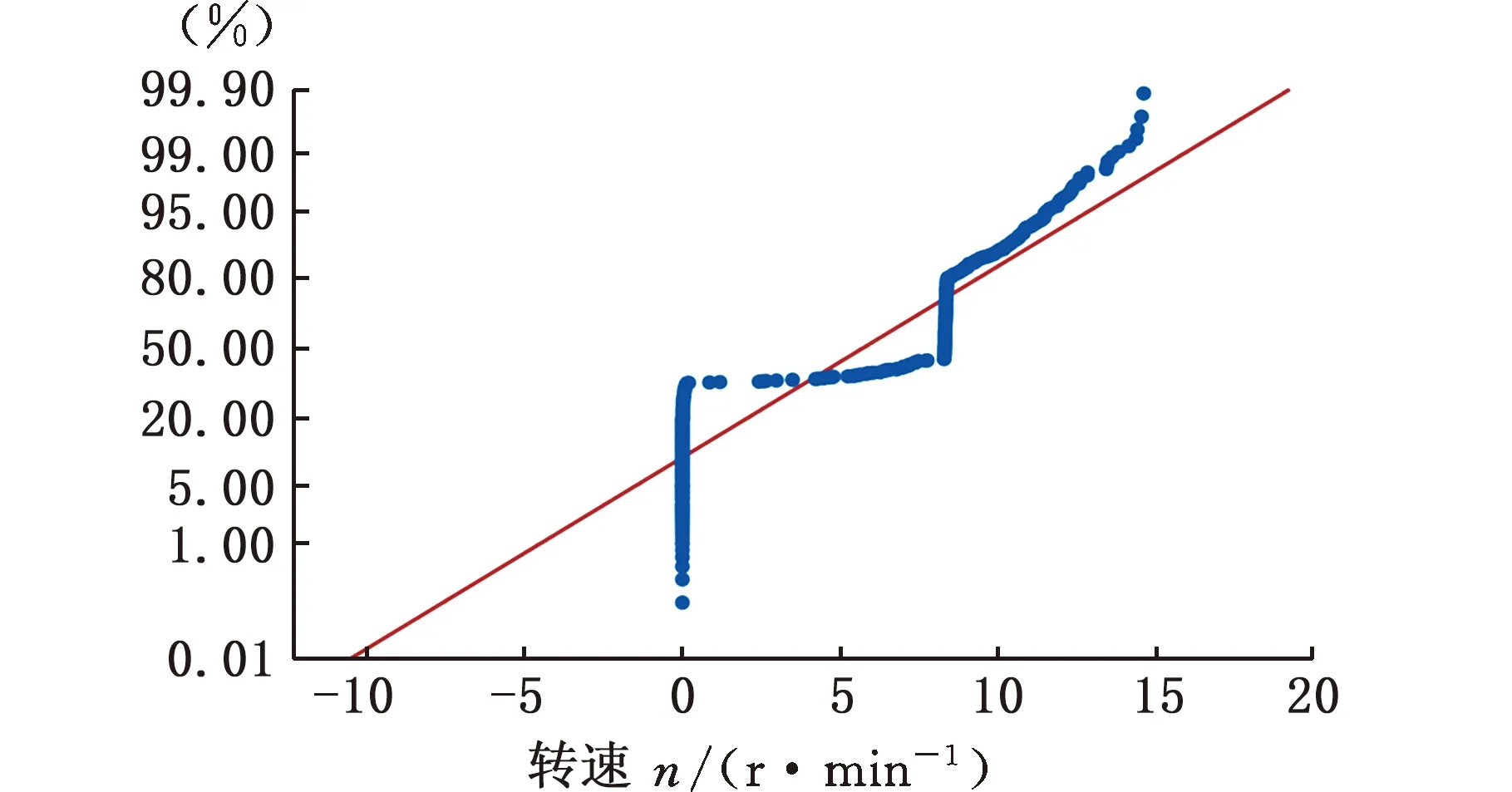
(a)风轮转速

(a)风轮转速

由于风轮转速的均值在3种可控运行状态下会有较大波动,故考虑均值变化的过程检测会导致误报率增加。采用经典的T2广义方差控制图对风力发电机的4种变量(风轮转速、电网A向电压、发电机冷却水温度、箱变油温)进行监控,其中,风机发电机原始运行数据如图3所示,控制图监控结果如图4所示。图3展示了风力发电机的4种变量的原始运行数据,该数据集包含风机正常运行数据、风机异常运行数据(液压系统主动压力过低)两种状态数据,其中,浅蓝色部分为风机正常运行数据,浅粉色部分为风机异常运行数据(液压系统主动压力过低)。运用T2广义方差控制图对图3中风力发电机的4种变量进行过程监控,设置子组大小为5,得到的控制图运行结果如图4所示。图4包含T2控制图部分(图4a)和广义方差控制图部分(图4b)。T2控制图部分是针对过程均值向量的监测,由于原始数据的过程均值受自然风速的影响波动较大,导致T2控制图在风机正常运行时会产生误报,同时对过程异常的报警也不明显。广义方差部分是针对过程协方差矩阵的监测(监测变量之间相关关系的变化),虽然受自然风速的影响,变量数据波动较大,但是变量之间的相关关系比较稳定,当过程发生异常时,变量之间的相关关系被打破,控制图监测到过程异常并报警。广义方差部分在过程异常时能够快速报警,虽然在正常运行时也会产生少量误报,但相对过程均值较为稳定。

(a)风轮转速

(a)T2控制图
本文以过程数据的协方差矩阵为研究对象,通过监测变量之间的相关关系来判断过程是否存在异常。同时,本文通过设计多模式过程监控方法、改进协方差估计方法、设计协方差检验统计量进一步减少过程的误报,实现风力发电机多模式数据的稳定过程监控。
图5为3种正常运行状态和3种故障状态下风力发电机的协方差矩阵图,F1~F12表示12个发电机运行状态变量:齿轮箱冷却水温度、风轮转速、机舱温度、报警状态、发电机冷却水温度、瞬时风速、箱变油温、发电机定子U温度、有功功率、座舱温度、低速轴承温度、高速轴承温度。与3种正常运行状态相比,3种故障状态(机舱冷却风扇异常、液压系统主压力过低、液压油泵马达异常)下的协方差矩阵变化很大。因此,在这种数据情况下对协方差进行监测是一种合适的在线监控策略。

(a)常态运行状态 (b)限功率运行状态 (c)负功率运行状态
2 研究方法
2.1 问题描述
假设μk,Σk(k=1,2,…,K)未知,定义多模式假设检验问题:
(1)
2.2 可控模式的协方差矩阵的估计

高维环境中协方差矩阵的估计已被广泛研究,经典的稀疏估计假设协方差中的大多数元素为零。然而,部分工业生产数据中的高维数据不满足这种稀疏假设,因此,协方差无法通过稀疏估计有效求解。本文使用YANG等[31]提出的线性收缩估计方法来估计协方差,从而获得更准确的协方差估计。从理论上来讲,该方法将协方差矩阵的对角矩阵与非对角矩阵分开估计,并且通过交叉验证策略求解最佳的收缩估计系数,使得该方法既能够适用于协方差稀疏估计场景,又能适用于协方差非稀疏估计场景。该方法适用性更广,在高维非稀疏情况下相较于传统方法具有明显的优势,同时在高维稀疏情况下也具有与传统方法相当的估计效果。本文结合滑动窗口策略,将线性收缩估计方法扩展到多模式数据场景,并且对收缩估计的目标矩阵进行了改进,本文设置的目标矩阵是从历史可控数据中习得的,能够进一步保证协方差估计方法的稳健性。

(2)
其中,ε是一个数值较小的系数,本文取ε=0.05。则上式可转化为
(3)

(4)

(5)

(6)
本节的可控模式下的协方差线性收缩估计方法适用性如下:①适用于n 获得1,2,…,K种可控运行模式的协方差矩阵Σk后,可以对新样本进行式(1)中的假设检验。 在协方差矩阵稀疏且漂移较小的情况下,ZHU等[25]针对假设 (7) 构建了一种检测方法,其中,kmax(X)表示矩阵X的最大特征值。通过比较协方差的最大特征值的差异来比较两个协方差矩阵,当两个协方差矩阵存在差别时,与L2和L∞类型检测相比,差分矩阵的最大特征值可以提取到更少的噪声。ZHU等[25]构建的统计量为 (8) (9) (10) (11) 本文采用MSPEWMA控制图对过程进行监控。将MSPEWMA控制图的统计量设置为 (12) 其中,λ是平滑系数。EWMA控制图通常取平滑系数λ为0.05、0.1或0.2。当λ取较小值时,它对小漂移更敏感。本文取λ=0.05。 模式之间的切换包括两类:可控模式之间切换,可控模式切换到失控模式。图6是一个模式切换的例子。可控模式1为过程均值向量为μ1、过程协方差矩阵为Σ1的正态分布数据,可控模式2、3同理。三种可控模式的均值向量是维度为p的零向量(μ1=μ2=μ3),协方差矩阵为参数不同的指数衰减型协方差矩阵: (a)MSPEWMA模式切换过程(统计量变化透视图) Σ1=(0.25|i-j|)p×pΣ2=(0.5|i-j|)p×p Σ3=(0.75|i-j|)p×p MSPEWMA控制图第I阶段监控过程如图7所示。MSPEWMA控制图的控制限计算方法步骤如下: 图7 MSPEWMA控制图第Ⅰ阶段监控Fig.7 MSPEWMA control chart monitoring of Ⅰ stage (1)设置平滑系数λ和滑动窗口W的值。 (2)设置模式过渡约束参数M。 (3)通过线性收缩估计来估计K个可控模式的协方差矩阵。 (4)设置MSPEWMA控制图检验统计量的初始值Z0=0。 (5)检验统计量计算(式(10)和式(12))和模式识别(式(11))。 (13) (6)根据EWMA滑动窗口的原理,依次计算Zn: (14) (7)设置ARL0,通过Monte Carlo模拟计算MSPEWMA控制图的UCL值。 图8 MSPEWMA控制图第Ⅱ阶段监控Fig.8 MSPEWMA control chart monitoring of Ⅱ stage MSPEWMA控制图的性能受数据分布F、可控样本量m0、数据维数p、漂移量δ、平滑参数λ和滑动窗口大小W的影响。这些参数设置如下。 (1)可控样本数m0:50、80、100、120、150。 (2)数据维度p:20、50、100、150、200。 (3)协方差漂移量δ:0.2、0.4、0.6、0.8、1.0。 (4)滑动窗宽度W:20、40、60、80、100。 (5)模式过渡参数M:1、2、3、4、5。 (6)数据分布F:①多元正态分布,记为Normp;②具有自由度ξ的多元t分布,记为tp,ξ,其中ξ=5;③多元Gamma分布,形状参数φ,记为Γp,φ,其中φ=3。 这四种方案覆盖了尽可能广泛的协方差漂移模式,如图9所示。在方案OC1和OC2中,漂移仅发生在协方差矩阵的前S个对角元素中,这表明协方差矩阵中的漂移比较稀疏。与OC1不同,OC2中的漂移在对角元素中具有不同的大小。OC3和OC4中的协方差矩阵比OC1和OC2中的协方差矩阵发生改变的元素更多,因此,OC3与OC4的稀疏性降低。在OC3中,偏移仅发生在一个子块中;而在OC4中,偏移发生在两个子块中。 (a)OC1:漂移量δ的S×S对角矩阵 (b)OC2:漂移量以5δ/S递进的S×S对角阵 在不同分布类型F、漂移量δ、滑动窗口宽度W、数据维度p、可控样本大小m0的条件下,控制图在失控状态下的性能如图10~图13所示。比较不同参数对MSPEWMA控制图的影响时,为了方便起见,只选择第4个协方差漂移模型OC4,因为该协方差漂移模式具有更好的通用性。其中,平均运行长度(average run length,ARL)表示从检测开始到控制图超出界限并发出警报为止,控制图所采集的平均样本数;δ是一个量纲一的量,表示平均位移的大小;滑动窗口W表示在MSPEWMA控制图的每次检测中从待测试样本中选择的样本点数量;数据维度p表示待测样本的变量数量;可控样本量m0表示每次检测从可控样本中提取的样本点数量。模式过渡参数M为控制图约束模式之间过渡状态的参数,表示发生模式过渡所需判断的样本点个数。 (a)Norm100,OC4 (b)t100,5,OC4 (c)Γ100,3,OC4图10 不同滑动窗口下MSPEWMA控制图OC-ARL值的比较Fig.10 Comparison of OC-ARL of MSPEWMA control chart under different sliding windows (1)滑动窗口W的影响。由图10可以看出,随着W的增加,三种分布的失控状态的平均运行长度OC-ARL值逐渐减小。其中,多元t分布的OC-ARL值降低程度更为明显。结果表明,滑动窗口宽度W越大,MSPEWMA控制图的控制效果越好。对于3种不同的分布,OC-ARL值随着W的增大而减小。而对于较大的漂移(δ=1.0),当W达到一定值(W=60)时,OC-ARL值在这种条件不会再随着滑动窗口的增大而减小。多元t分布的OC-ARL值的减少程度比多元正态分布和多元Gamma分布的减少程度更明显。总地来说,滑动窗口宽度越大,MSPEWMA控制图的控制效果越好。 (2)数据维度p的影响。由图11可以看出,对于多变量正态分布、多变量t分布和多变量Gamma分布,OC-ARL值随着p的增大而减小。对于δ=0.2,δ=0.4和δ=0.6,OC-ARL值随着 (a)Normp,OC4 (b)tp,5,OC4 (c)Γp,3,OC4图11 MSPEWMA控制图不同维度OC-ARL值的比较Fig.11 Comparison of OC-ARL of MSPEWMA control chart in different dimensions p的增大而减小。对于δ=0.8和δ=1.0,OC-ARL值已经达到了一个相对较低的值,不再随着p的增大而减小。总之,OC-ARL值随着数据维度的增加而逐渐减小并达到较低的值。因此,数据维度越高,MSPEWMA控制图的控制效果越好,MSPEWMA控制图在处理高维数据方面表现良好。 (3)可控样本量m0的影响。由图12可以看出,随着可控样本量的增加,三种分布的OC-ARL值逐渐减小,但降幅明显小于滑动窗口和数据维度,证明MSPEWMA控制图不需要过多的可控样本量。对于3种不同的分布,OC-ARL值随着可控样本大小m0的增加而减小,当m0达到约100时,即使m0增大,OC-ARL值也不再增大。另外,多元t分布和多元Gamma分布的下降速度相较于多元正态分布更快。因此,针对数据分布的小漂移(δ较小)时,可控样本量越大,MSPEWMA控制图的控制效果越好。针对数据分布的大漂移(δ较大)时,即使设置较小的可控样本量,也能取得较优的监测性能。 (4)漂移量δ的影响。由图10~图12可以看出,随着漂移量的增大,三种分布的OC-ARL值逐渐减小。其中,当δ为0.8或1时,MSPEWMA控制图在3种分布下均有较小的OC-ARL值,证明MSPEWMA控制图在大漂移情况下具有良好的监测效果。 (5)模式过渡参数M的影响。模式过渡约束参数M表示当M个连续的统计量超出控制限时才判断过程发生模式转换(失控模式切换/可控模式切换),因此OC-ARL的最小值是M。由图13可以看出,在具有较小漂移(如δ=0.2,0.4)的模型中,随着M的增大,OC-ARL值逐渐减小;而针对具有较大漂移(如δ=0.8,1)的模型,因为OC-ARL的最小值与M有关,M的增大会导致OC-ARL值的增大,因此,监测协方差矩阵元素的大漂移时,建议采用较小的M值。 选择3个经典协方差控制图与所提的MSPEWMA图进行比较:SLED(ZHU等[25])、CLX(CAI等[24])和LC(LI等[23])。可控平均运行长度IC-ARL0设置为200。通过Monte Carlo随机模拟获得控制图的平均运行链长。在相同的IC-ARL设置下,OC-ARL值越小,控制图的性能越好。 3.3.1单模式下与其他方法的比较 详细描述模拟的5个因素对MSPEWMA控制图监控效果的影响。考虑四种协方差漂移模型,漂移大小δ考虑总共5个水平(0.2, 0.4, 0.6, 0.8, 1.0)。通过Monte Carlo模拟求解数据的OC-ARL值。在105次仿真的条件下,当可控样本量m0=100,维度p=100,滑动窗口宽度W=50时,将所提的MSPEWMA控制图与基于协方差检验的常用控制图进行了比较,如图14~图17所示。 (a)Norm100,OC1 (b)t100,5,OC1 (c)Γ100,3,OC1图14 漂移模型OC1条件下MSPEWMA与其他控制图OC-ARL值的比较Fig.14 Comparison of MSPEWMA with other control charts OC-ARL under drift model OC1 conditions (1)漂移量。与其他多变量非参数控制图相比,对于δ=0.2,δ=0.8和δ=1.0条件, MSPEWMA控制图的OC-ARL值更小,即使在某些情况下差异较小,如图14b所示。对于δ=0.4和δ=0.6条件,除了图16a和图16b,MSPEWMA控制图的OC-ARL值也相对更小,尤其是对于OC1,可以清楚地看到新方法的优势。综上,MSPEWMA控制图在各种漂移量的情况下均具有良好的监测效果。 (2) 数据分布。MSPEWMA控制在3种不同的数据分布下均具有良好的控制效果。根据图14~图17,对于多元Gamma分布,MSPEWMA在4种控制图中表现最佳。对于多元正态分布,MSPEWMA相对表现最优(除了图16中OC3条件下δ=0.4和δ=0.6)。对于多元t分布,MSPEWMA相对表现最好(除了图15b中OC2条件中的δ=0.6和图16b模型OC3条件中的δ=0.6)。总之,MSPEWMA控制图在三种不同的数据分布中总体来说具有更好的监控效果。因此,MSPEWMA控制图具有较好的通用性,可以有效地监控不同分布的数据。 (a)Norm100,OC2 (b)t100,5,OC2 (c)Γ100,3,OC2图15 漂移模型OC2条件下MSPEWMA与其他控制图OC-ARL值的比较Fig.15 Comparison of MSPEWMA with other control charts OC-ARL under drift model OC2 conditions (a)Norm100,OC3 (b)t100,5,OC3 (c)Γ100,3,OC3图16 漂移模型OC3条件下MSPEWMA与其他控制图OC-ARL值的比较Fig.16 Comparison of MSPEWMA with other control charts OC ARL under drift model OC3 conditions (a)Norm100,OC4 (b)t100,5,OC4 (c)Γ100,3,OC4图17 漂移模型OC4条件下MSPEWMA与其他控制图OC-ARL值的比较Fig.17 Comparison of MSPEWMA with other control charts OC-ARL under drift model OC4 conditions (3)协方差漂移模型。根据图14~图17,相较于其他方法,对于协方差漂移模型OC1和OC4,MSPEWMA控制图具有更好的监测性能,特别是在第一种协方差漂移模型OC1的情况下,MSPEWMA控制图的优势更明显。对于协方差漂移模型OC2和OC3,由图15c和图16c可以发现,MSPEWMA控制图在多元Gamma分布中表现更好。综上,在四种协方差结构下,MSPEWMA控制图在大多数情况下都有更好的监测性能。 3.3.2多模式下与其他方法的比较 为了获得控制图在多模式数据下的性能,进行了多模式仿真,以检验所提的MSPEWMA控制图的特性。四种模拟场景设计如图18所示。通过Monte Carlo随机模拟方法获得MSPEWMA控制图可控状态的平均运行长度IC-ARL;同理,求解MSPEWMA控制图失控状态的平均运行长度OC-ARL。在三种数据分布下,考虑以下模拟场景:①多元正态分布,记为Normp;②多元t分布,自由度为ξ,记为tp,其中ξ=5;③多元Gamma分布Γp,φ,形状参数φ=3。每个数据分布包含200个采样点,三个分布在时间轴上以随机方式交替,以此来构建可控状态的模拟数据集。失控状态的参数设置同3.2节中的仿真设置,另外设置过渡约束参数M=1,2,4。 图18 多模仿真中三种数据分布的随机变换过程Fig.18 Random transformation process of three data distributions in multimode simulation 根据图18中的多模式条件,将MSPEWMA与多模式数据条件下的其他控制图进行比较。在四种不同协方差漂移的条件下,当m0=100,p=100,滑动窗口W=50时,MSPEWMA控制图均具有更好的监测效果,如图19~图22所示。在OC2情况下,相较于其他控制图,MSPEWMA具有更优的监控效果。相比于其他控制图在小漂移下的表现,MSPEWMA控制图能够有效监测协方差小漂移。相较于其他控制图在大漂移下的表现,MSPEWMA控制图具有明显的优势。横向对比过渡约束参数M对控制图的影响,当M取较小的值(如M=1,2)时,对于监控协方差矩阵中的大漂移具有明显的优势;当M取较大的值(如M=4)时,能更好地监控协方差矩阵的小漂移。另外,针对协方差矩阵中大多数元素发生漂移的情况(如OC2,OC4),取更小的M值能获得更优的过程监控效果;当协方差矩阵中少数元素发生漂移时,取较大的M值能获得更稳健的监控效果。理论上来讲,M越大,控制图的策略相对来说会更保守(可以理解为,M取较大值时,ARL值的方差较小,但ARL的均值较大);M越小,控制图的策略相对来说会更激进一些(可以理解为,M取较大值时,ARL值的方差相对较大,但ARL的均值相对较小)。 (a)M=1,OC1 (b)M=2,OC1 (c)M=4,OC1图19 多模式数据条件OC1下MSPEWMA与其他控制图OC-ARL值的比较Fig.19 Comparison of MSPEWMA with other control charts OC-ARL under multimode data conditions OC1 (a)M=1,OC2 (b)M=2,OC2 (c)M=4,OC2图20 多模式数据条件OC2下MSPEWMA与其他控制图OC-ARL值的比较Fig.20 Comparison of MSPEWMA with other control charts OC-ARL under multimode data conditions OC2 (a)M=1,OC3 (b)M=2,OC3 (c)M=4,OC3图21 多模式数据条件OC3下MSPEWMA与其他控制图OC-ARL值的比较Fig.21 Comparison of MSPEWMA with other control charts OC-ARL under multimode data conditions OC3 (a)M=1,OC4 (b)M=2,OC4 (c)M=4,OC4图22 多模式数据条件OC4下MSPEWMA与其他控制图OC-ARL值的比较Fig.22 Comparison of MSPEWMA with other control charts OC-ARL under multimode data conditions OC4 能源需求的增加促使风电场直径扩大,风力发电机的状态监测逐渐成为研究重点。本节利用MSPEWMA控制图对风电场的SCADA数据集进行状态监测。当自然风速较小时,风力发电机处于负功率运行状态;当自然风速极高时,风力发电机处于限功率状态;将正常风速区间的风机运行状态称为常态功率运行状态。风机呈现出多模式运行场景,监控协方差比均值更加恰当,并且在正常运行时,协方差统计量也能提取更多故障信息,具有更小的噪音。 本节选择18号风机的“液压系统主压力过低”故障,并依据第1节的介绍将风机状态分为“负功率运行、限功率运行和常态功率运行”。研究了MSPEWMA控制图在三种数据模式下对故障数据的监测效果。从SCADA数据集40余个变量中剔除了数据波动较小、数据正常或异常状态下无差异的变量,进而提取了12个变量:齿轮箱冷却水温度、风轮转速、机舱温度、报警状态、发电机冷却水温度、瞬时风速、箱变油温、发电机定子U温度、有功功率、座舱温度、低速轴承温度、高速轴承温度。在正常样本数据集中,随机选择m0=100作为可控样本,并将控制图的基本参数设置为ARL0=200,λ=0.05,W=20,其中,ARL0为可控状态下的平均运行链长,λ为平滑系数,W为滑动窗口宽度。首先,根据控制图参数的设置,利用可控数据集获得控制限。待监测的样本由随机选择的200个可控样本数据和200个失控样本数据组成。其中,可控样本包括3种模式:负功率运行模式、限功率运行模式、常态功率运行模式。失控样本为该风机的“液压系统主压力过低”故障。运用MSPEWMA控制图对待检测样本进行监控,获得的控制图见图23。 在第一种情况下,如图23a、图23d、图23g、图23j所示,系统从常态功率运行状态下过渡到故障状态。MSPEWMA控制图在故障发生后的第3个观测点发出警报,而SLED在第9个观测点,CLX在第8个观测点,LC在第4个观测点报警。在第二种情况下,如图23b、图23e、图23h、图23k所示,系统从限功率状态转变为故障状态。MSPEWMA控制图在故障发生后的第2个观测点发出警报,而SLED在第7个观测点,CLX在第11个观测点,LC在第6个观测点报警。在第三种情况下,如图23c、图23f、图23i、图23l所示,系统从负功率状态转变为故障状态。MSPEWMA控制图在故障发生后的第2个观测点发出警报,而SLED在第12个观测点,CLX在第9个观测点,LC在第11个观测点报警。综上所述,与其他3种控制图相比,本文提出的MSPEWMA控制图对异常数据更敏感,报警更快,监控效果更好。 针对工业数据监测的几个挑战:多模式性、高维性、非正态性,本文设计了一种考虑模式约束的基于协方差检验的多模式在线监测方法——MSPEWMA控制图,并且结合SCADA系统采集的风机实际数据验证了所提方法的有效性和准确性。通过与其他方法的仿真分析与实例分析,得到以下结论: (1)MSPEWMA控制图针对小漂移的条件在大部分情况下表现更好,针对大漂移的条件表现始终良好,证明MSPEWMA控制图具有更优的监测性能。 (2)对于监控分布未知的数据,MSPEWMA控制图在正态和非正态数据方面都表现良好,证明MSPEWMA控制图具有更好的通用性,适用于数据分布未知的监测任务。 (3)MSPEWMA控制图采用模式过渡约束参数M的策略,并且研究了约束参数M对控制图性能的影响,给出在不同的监控状况下约束参数M的建议值,使得控制图能够有效处理模式之间的过渡状态,进一步减少由模式之间的过渡引起的控制图误报。2.3 稀疏主特征值检验统计量的构建



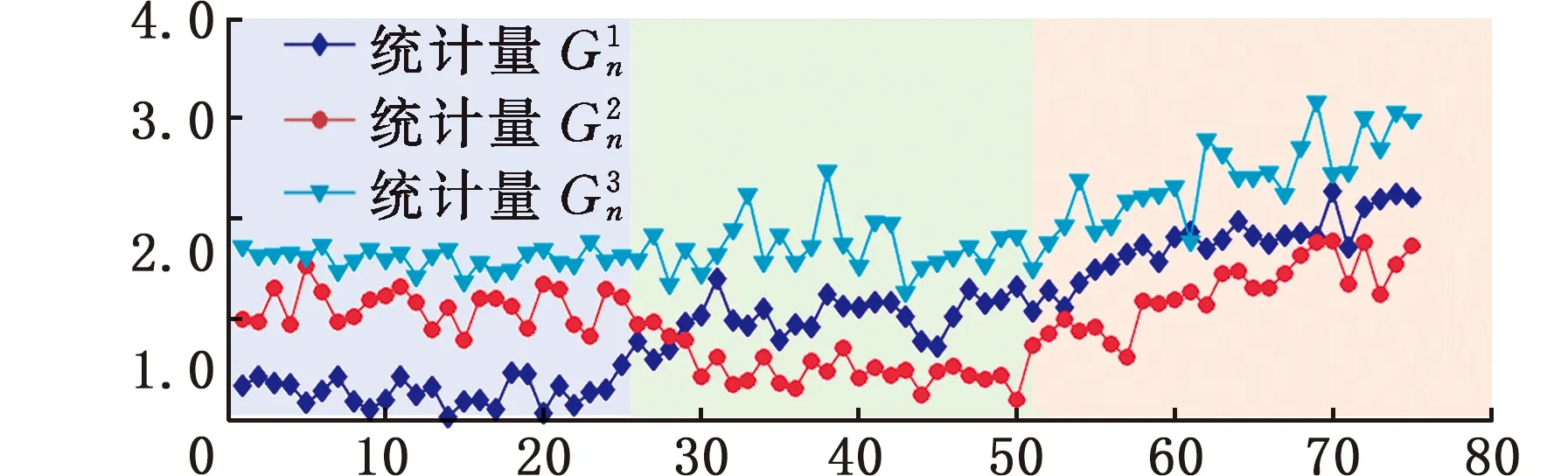
2.4 MSPEWMA控制图设计









3 模型评估与对比
3.1 模型参数设计



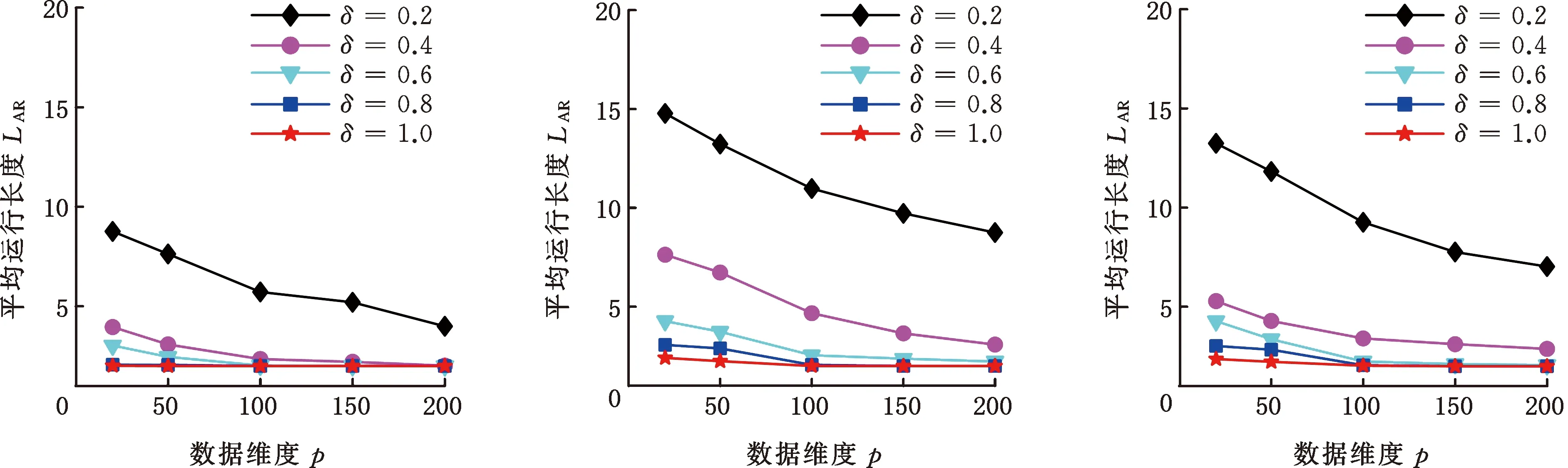
3.2 不同参数对MSPEWMA控制图的影响

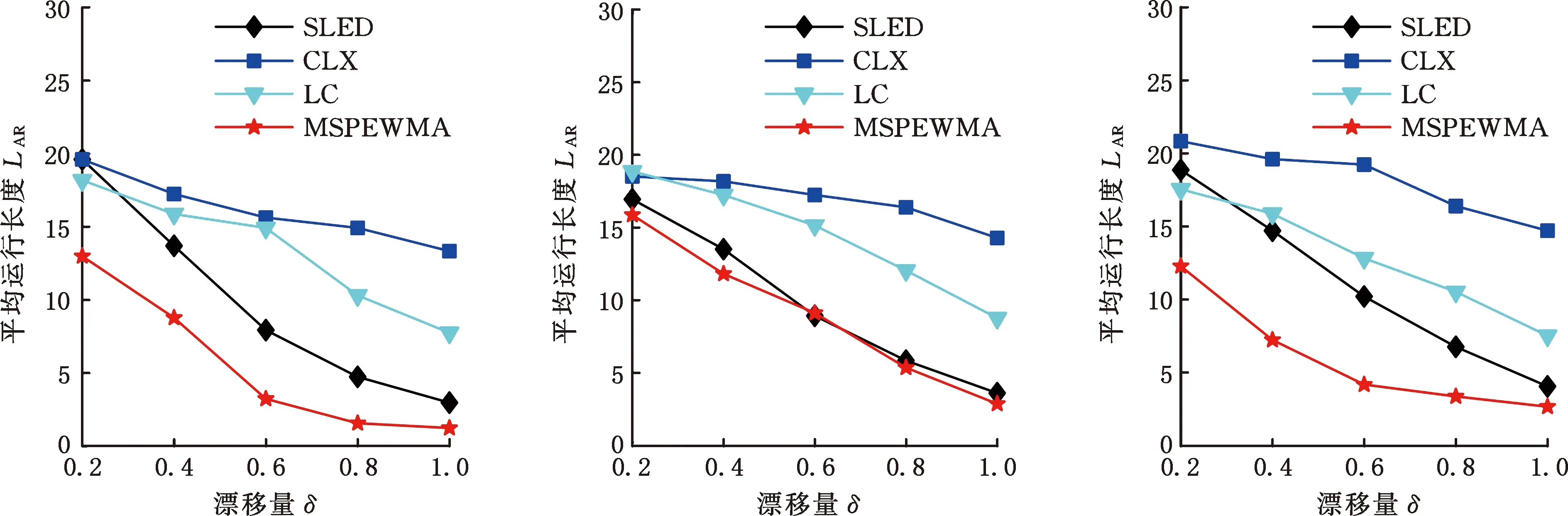
3.3 与其他方法的性能比较








5 实例分析
6 结论

