采用圆渐开线的非对称等壁厚涡旋型线设计与性能研究

侯才生 李金虎 刘 宇 马 辉

宁夏大学机械工程学院,银川,750021

0 引言

涡旋压缩机因具有噪声低、可靠性高、结构简单、质量小等诸多特点而广泛应用于工业、医疗、食品、制冷、各种气体压缩等领域[1-3]。近年来,汽车用涡旋压缩机的相关研究如火如荼[4-5],尤其是随着新能源汽车的兴起与蓬勃发展,涡旋压缩机的应用前景更加广阔。

涡旋型线是研究涡旋压缩机的关键,它对压缩机性能的影响至关重要[6],因此一直是研究的热点问题。目前,涡旋型线主要有等壁厚型线和变壁厚型线两大类。第一类型线通常由单一曲线构成,如基圆渐开线[7]、线段渐开线[8]、正多边形渐开线[9]等;第二类型线由两条及以上的单一曲线组合而成,如圆渐开线—三次曲线—圆渐开线的组合[10]、不同极径的代数螺线组合[11]、圆渐开线—高次曲线—变径基圆渐开线的组合[12]、圆渐开线—高次曲线—圆弧的组合[13]等。对于等壁厚型线的涡旋压缩机,因其承受的气体作用力波动较小,设计加工较为方便,所以在实际应用中普遍使用,尤其是基圆渐开线构成的型线已经商品化,但此类型线也存在明显缺陷,如压缩比不高、行程容积较小等。对于变壁厚型线的涡旋压缩机,虽然弥补了等壁厚型线的缺陷,具有较大的行程容积和较高的压缩比,但在实际应用中却困难重重,原因如下：①该型线是一种组合型线,加工制造和测量都比较困难;②该型线的涡旋压缩机承受的气体作用力变化幅度较大,传热过程较复杂。

上述研究成果表明,无论是等壁厚型线还是变壁厚型线都各具优势,且能适应不同的性能要求,但也存在着不足之处。由此,深入研究构成涡旋齿的型线,探究出一种既能提高涡旋压缩机综合性能,又能降低加工测量困难的涡旋型线,对推动涡旋压缩机应用和产业化是十分必要且极具实际意义的。本文提出采用基圆渐开线的非对称等壁厚涡旋型线设计方法,为解决上述难题提供了新思路,该方法在进行型线构建时既考虑等壁厚型线的优势,又兼顾型线便于加工测量的特点,能有效提高涡旋压缩机的综合性能。

1 几何模型

1.1 型线方程

如图1所示,M为基圆渐开线上的任意一点,φ为M点处所对应的切向角,Rg为任意渐开线基圆半径,Rs为展弦。由微分几何中的曲线理论可知,要使涡旋型线能在任意一点处正确啮合,须满足关系式：

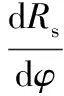
(1)

根据上述描述,基圆渐开线所对应的母线方程为

(2)

φ∈[0,φmax]Rs=aφ

式中,a为基圆半径;φmax为型线的最大切向角。

由于动、静两涡旋齿均为有形的实体,需要有一定的壁厚,故母线方程确定后,根据法向等距线的特点,可得到两涡旋齿的内外壁型线方程：

(3)

式中,t1为静涡旋齿的壁厚;t2为动涡旋齿的壁厚,且满足t2>t1;Ror为回转半径;θ为主轴转角;下标f和m分别表示静涡旋齿与动涡旋齿;下标i和o分别表示内壁和外壁。

根据式(3),可得到动、静涡旋齿的几何模型,如图2所示。由图2可以明显看出,虽然两涡旋齿从齿头到齿尾处各自的壁厚都相等,但动涡旋齿的壁厚值要明显大于静涡旋齿的壁厚值,即两涡旋齿是一种非对称的等壁厚涡旋齿。

1.2 壁厚与回转半径之间的关系

图3中A、B两点之间的距离lAB等于静涡旋齿的壁厚t1,C、D两点之间的距离lCD等于动涡旋齿的壁厚t2。动、静涡旋齿在运行过程中,当任意一对共轭点接触时,两涡旋齿的中心距离为一常量,即回转半径Ror,故B、C两点之间的距离lBC等于回转半径的两倍。此时,动、静涡旋齿的壁厚与回转半径之间的关系为

图3 涡旋齿壁厚与回转半径的关系Fig.3 Relation between scroll tooth thickness and rotating radius

t1+t2+2Ror={[xm,o(φ+2π)-xm,o(φ)]2+

[ym,o(φ+2π)-ym,o(φ)]2}1/2

(4)

2 型线的容积性能

动、静涡旋齿相互啮合时,动涡旋齿的内壁型线与静涡旋齿的外壁型或动涡旋齿的外壁型线与静涡旋齿的内壁型线会形成数对封闭的“月牙形”工作腔体,如图4所示。这些封闭腔体由内到外依次称为第一压缩腔(又称排气腔)、第二压缩腔和第三压缩腔(又称吸气腔),用代号①、②、③表示。各对压缩腔的容积会随着主轴转角θ的变化而变化。为便于分析计算,规定当主轴转角θ=0°时,最外侧压缩腔开始准备进入吸气过程。在形成压缩腔体的过程中,会出现一系列的啮合点,见图4中的点M、N、P、M′、N′和P′,这些啮合点为各个压缩腔的分界点。由涡旋型线构成原则可知,同一个啮合点上一对共轭型线的切向角大小相差π,即

图4 涡旋压缩机的压缩腔Fig.4 Compression chamber of scroll compressor

φo=φi+π

(5)

令xf,i=xm,o,yf,i=ym,o,可求得静涡旋齿内壁型线啮合点处对应的切向角

(6)

式中,k为啮合点的标号,k=1,2,…。

动涡旋齿外壁型线啮合点处对应的切向角

(7)

同理,可求得静涡旋齿外壁型线与动涡旋齿内壁型线在啮合点处对应的切向角。图4中各啮合点处的切向角见表1。

2.1 工作腔几何容积

如图5所示,以静涡旋齿内壁面与动涡旋齿外壁面围成的第二压缩腔为例,对单一“月牙形”腔体面积进行计算。

(a)单一腔体

由图5a易得第二压缩腔单一“月牙形”腔体面积为涡旋型线Lf,i所围成的面积与涡旋型线Lm,o所围成的面积之差,该“月牙形”腔体面积可通过法向等距线法计算,转换为求解图5b等宽度环槽形状腔体的面积,则有

(8)

同理可得第三压缩腔单一“月牙形”腔体面积

(9)

因此,涡旋压缩机的第n(n≥2)个压缩腔容积可表示为

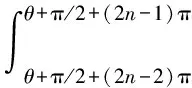
(y′)2)1/2dφ

(10)

式中,h为涡旋齿高度。

对于排气腔,其容积与开始排气角及齿头处涡旋型线的修正情况有关。如图6所示,本文采用双圆弧的修正方法对齿头进行修正。

图6 双圆弧修正齿头Fig.6 Modified tooth using twin-pairs of circular arcs

根据主轴转角θ的变化,将排气腔容积的计算划分为两个阶段进行。在第一阶段,排气腔由构成动、静涡旋齿的基圆渐开线和修正圆弧组成,如图7a所示。此时其腔体的容积

(a)第一阶段 (b)第二阶段图7 排气腔容积Fig.7 Discharge chamber volume

(φ+π+∂)3-(φ+π-∂)3]-

a2h(π-4∂)-2hSm

(11)

式中,φ为修正展角;∂为渐开线发生角;λ为修正圆弧中心角;Rd为修正大圆弧半径;Rx为修正小圆弧半径。

如图7b所示,在第二阶段,排气腔完全由2条修正大圆弧和2条修正小圆弧构成,其容积为

(12)

2.2 行程容积与压缩比

对于涡旋压缩机,行程容积和压缩比是非常重要的容积性能指标,对压缩性能和整机容积效率的影响较大。这两个性能指标值越大,意味着涡旋压缩机的工作性能就越好。

当主轴转角θ=0°时,前一吸气过程结束,最外侧压缩腔开始准备进入新的吸气过程,此时最外侧的第三压缩腔形成最大的工作腔体,将这一时刻的第三压缩腔定义为行程容积,用V3(0)来表示。将行程容积V3(0)与压缩终了时刻工作腔容积的比值定义为压缩比,表示为

(13)

式中,κ为气体的等熵指数,本文取κ=1.21;θ*为开始排气角,θ*=2π-γ。

3 型线的动力学性能

作用在动、静涡旋齿上的气体作用力主要有轴向气体力Fa、切向气体力Ft和径向气体力Fr三种。由图4可知,涡旋压缩机的各同名压缩腔都是对称的,故动、静两涡旋齿上承受着相同的气体作用力。作用在静涡旋齿上的气体力主要会引起涡旋压缩机的振动,但由于在主轴转动的一个周期内,这些气体力的变化幅度很小,所以通常忽略不计。然而,作用在动涡旋齿上的气体力会直接影响涡旋压缩机的整机效率,因此本文着重分析作用在动涡旋齿上的各种气体作用力。

3.1 轴向气体作用力

轴向气体力是作用在动涡旋齿上的最重要作用力,也是涡旋压缩机的主要缺点之一。该力会使动、静涡旋齿相互脱离,造成两齿之间的轴向间隙过大,径向泄漏量增加。为减少径向泄漏量,提高涡旋压缩机的整机效率,就必须使作用在动涡旋齿上的轴向气体力较小。图8所示为作用在动涡旋齿上的轴向气体力,在主轴转过一周的过程中,轴向气体力可表示为

图8 作用在动涡旋齿上的轴向气体力Fig.8 Axial gas force on orbiting scroll tooth

(14)

式中,Ps为吸气压力。

3.2 切向气体作用力

切向气体力是由于各个相邻压缩腔体内的气体压力不相等而产生的一种作用力,该力的存在会使动涡旋齿产生自转力矩,进而使得两涡旋齿之间的摩擦增加,径向间隙增大。图9所示为作用在动涡旋齿上的切向气体力,在主轴转动一周的过程中,切向气体力可表示为

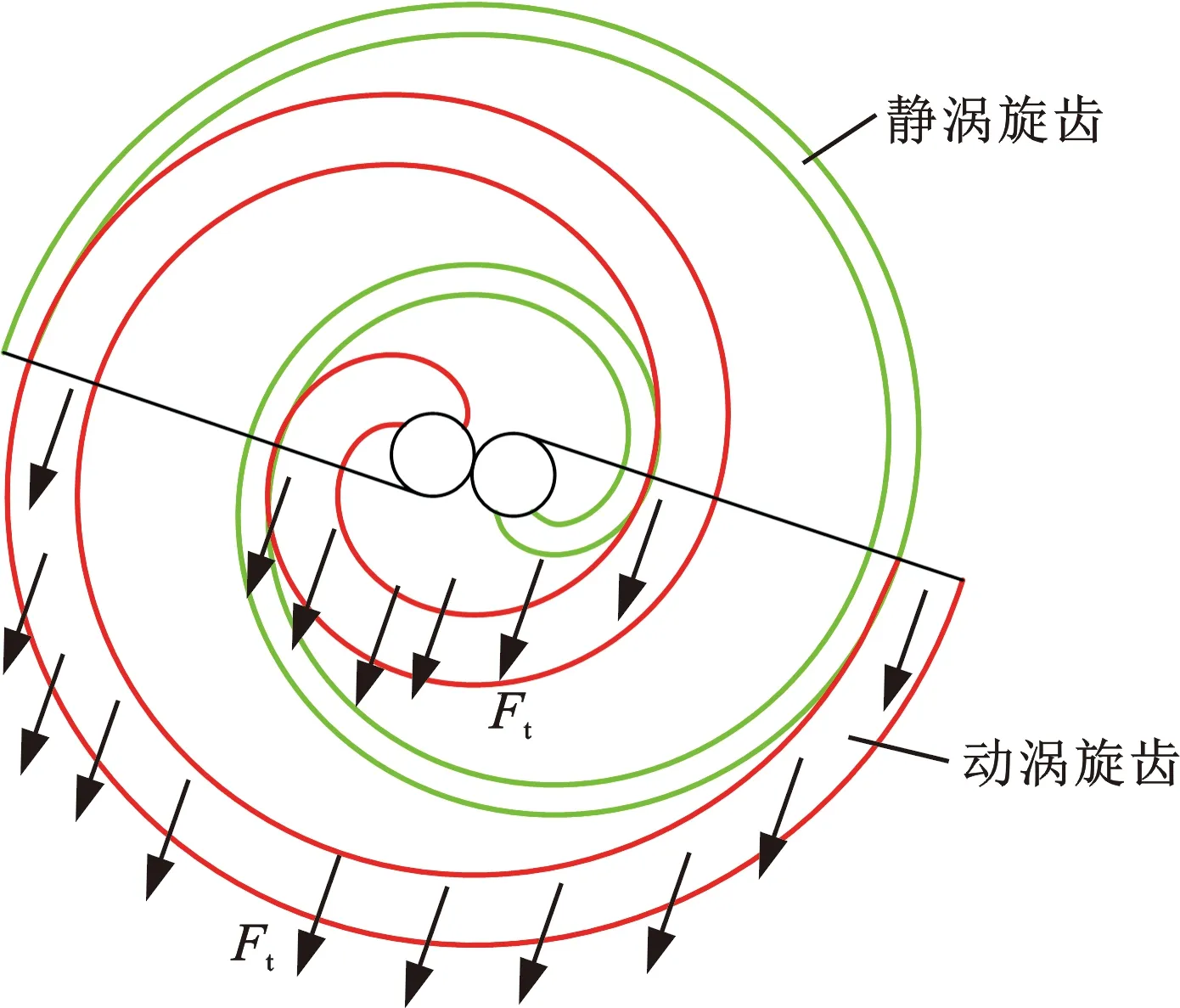
图9 作用在动涡旋齿上的切向气体力Fig.9 Tangential gas force on orbiting scroll tooth

Ft(θ)=2ha[θ+2(n-1)π](Pn-Pn+1)

(15)

0≤θ≤2π

3.3 径向气体作用力

沿动、静涡旋齿基圆中心连线方向施加在动涡旋齿上的气体力称为径向气体力,该力的作用效果是增加了切向气体的泄漏量,图10所示为作用在动涡旋齿上的径向气体力。在主轴回转一周的过程中,径向气体力可表示为

图10 作用在动涡旋齿上的径向气体力Fig.10 Radial gas force on orbiting scroll tooth

Fr(θ)=2ha(Pn-Pn+1)

(16)

0≤θ≤2π

4 性能分析与评价

当设计参数为：基圆半径a=2.069 mm,静涡旋齿壁厚t1=3 mm,动涡旋齿壁厚t2=5 mm,涡旋齿高h=35 mm,最大切向角φmax=6π,对称等壁厚型线涡旋齿壁厚取3 mm时,将新构建的非对称等壁厚型线与对称等壁厚型线及文献[14]中的变壁厚型线进行对比,结果见表2。

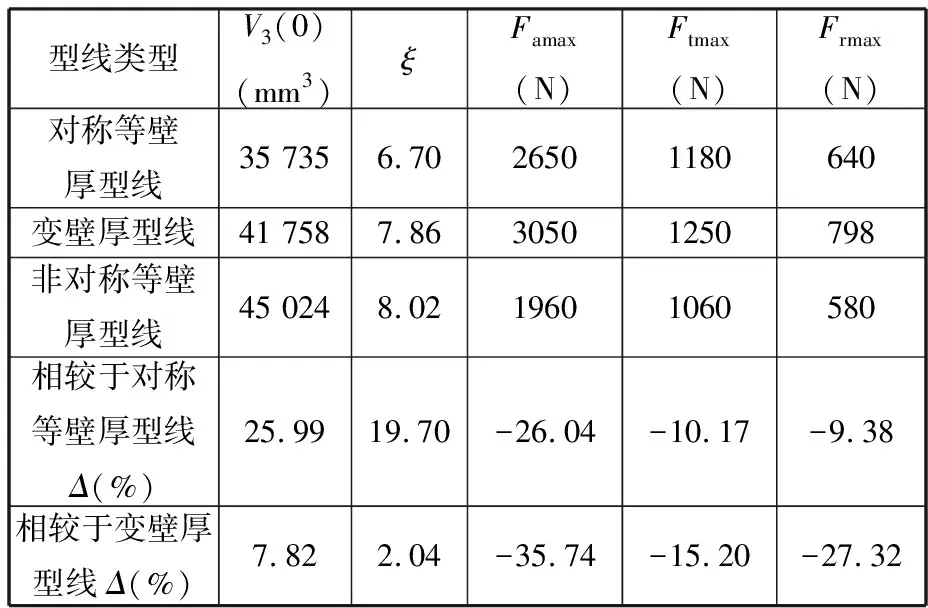
表2 涡旋型线性能对比

由表2可以看出,所采用的非对称等壁厚涡旋型线,无论在容积性能方面还是在动力学性能方面均比对称等壁厚型线和变壁厚型线性能更好。具体而言,在容积性能方面,相较于传统的对称等壁厚型线,其行程容积和压缩比分别提高了25.99%和19.70%;相较于变壁厚型线,行程容积和压缩比分别提高了7.82%和2.04%。在动力学性能方面,最大轴向气体力、切向气体力和径向气体力也显著减小,与对称等壁厚型线相比,三者分别减小了26.04%、10.17%和9.38%;与变壁厚型线相比,三者分别减小了35.74%、15.20%和27.32%,而较小的气体力才有益于提高涡旋压缩机的整机效率。

图11～图13所示为三种气体作用力在主轴回转一周过程中的变化曲线。总体来看,非对称等壁厚涡旋型线的轴向气体力、切向气体力和径向气体力均是最小的,而变壁厚型线所承受的三种气体力明显是最大的,由此也验证了本文方法的正确性。另外也可看出,在三种气体作用力中,轴向气体力最大,径向气体力最小,而切向气体力介于中间,这也印证了轴向气体力是涡旋压缩机的主要缺点之一。

图11 轴向气体力变化曲线Fig.11 Axial gas force changing curve

由图11可以看出,变壁厚型线的轴向力明显大于另两种型线,变化趋势为随着主轴转角θ的增加先逐渐减小后逐渐增大。对称等壁厚型线与非对称等壁厚型线的轴向力都是随着主轴转角θ的增加先逐渐减小后逐渐增大,轴向力达到最大值后又开始变小,但非对称等壁厚型线在轴向力达到最大值后,减幅更大,这极大地改善了涡旋压缩机的力学性能。

由图12可以看出,变壁厚型线的切向力变化趋势为随着主轴转角θ的增加先增大,增大到最大值后又开始减小。相对于其余两种型线,虽然切向力变化趋势都一致,即随着主轴转角θ的增加切向力先减小后增大,增大到最大值后又开始减小,但非对称等壁厚型线的切向力整体上要比等壁厚型线的切向力小很多。

图12 切向气体力变化曲线Fig.12 Tangential gas force changing curve

由图13可以看出,三种型线的径向力在变化过程中会呈现出一定的波动性,具体表现在径向力会由小变大、也会由大变小,这种波动会对径向间隙的密封产生不利影响,只有减小这种波动值才能有效抑制通过径向间隙的泄漏量。虽然非对称等壁厚型线的径向力也存在波动,但与变壁厚型线及对称等壁厚型线相比,波动值较小,这也在一定程度上改善了径向间隙的密封状况。

图13 径向气体力变化曲线Fig.13 Radial gas force changing curve

5 结论

(1)采用基圆渐开线构建了一种非对称的等壁厚涡旋型线,该型线既充分发挥了单一基圆渐开线的优势,又打破了以往型线设计中动、静涡旋齿相同的束缚。

(2)相较于传统的对称等壁厚型线和变壁厚型线,新构建的非对称等壁厚型线不仅具有较大的压缩比和行程容积,而且所承受的轴向力、切向力和径向力都较小,证实了非对称等壁厚型线在容积性能和动力学性能中的优越性。