基于属性加密的块级云数据去重方案

葛文婷，李卫海，俞能海

基于属性加密的块级云数据去重方案

葛文婷，李卫海，俞能海

（中国科学技术大学网络空间安全学院，安徽 合肥 230026）

针对已有的云数据去重方案主要集中在文件级去重。提出了一种基于属性加密的支持数据块级去重的方案，对文件级和数据块级做双粒度去重，并由属性加密实现数据共享。在混合云架构上设计算法，私有云根据文件标签和数据块标签进行重复性检测和一致性检测，并由块级标签建立默克尔树，支持对用户进行所有权证明。用户上传密文，私有云应用线性秘密共享技术，向密文添加访问结构和辅助信息，并为新的拥有权限的用户更新整体的密文信息。由私有云做代理重加密和代理解密，在无法获得明文的情况下承担大部分计算，减轻用户的计算时间开销。处理好的密文和标签存入公有云中，由私有云进行存取。安全性分析表明，所提方案在私有云可达到PRV-CDA（privacy chosen-distribution attacks）安全。分别对固定分块大小改变属性个数和固定属性个数改变分块大小两种情况进行仿真实验，应用4种椭圆曲线加密测试密钥生成、加密和解密计算时间，结果符合线性秘密共享的特性。仿真实验和开销分析表明所提方案可提升去重效率，并降低计算时间开销。

数据去重；云存储；属性加密；所有权证明；线性访问结构

0 引言

随着云计算技术的发展，使用云存储服务的用户日益增多，而大量重复数据的存储增加了网络传输带宽与存储的开销，降低了存储利用率。因此，大规模云存储系统往往需要去除重复的冗余信息，即去重技术[1]，以节省存储开销。在去重技术中，通用方式是为文件计算特定的标签并存储于服务器，对待上传文件进行重复性检测，进而判断用户是否需要上传文件。对于重复性文件，服务器无须再重复存储，从而达到节省带宽和提高存储利用率的目的。去重多见于文件级[2]的去重，即只检测整个文件是否重复。几乎相近的文件显然会重复占用存储空间。文献[3]的BL-MLE（block-level message-locked encryption）方案将文件分割成固定大小的数据块，实现数据块级的去重，并能检验数据块与文件的一致性。文献[4]在BL-MLE的基础上提出一种高效更新数据的方案，但未考虑数据共享。目前未见属性加密应用于块级去重，而属性加密可实现高效的数据共享和细粒度的访问控制。

用户为保护数据安全与隐私，往往会将数据加密后再上传云存储系统，这使得云存储系统在去重时必须考虑用户对数据的加密。属性加密（ABE，attribute-based-encryption）实现了一对多的访问控制以实现数据共享。现有的ABE方案有密钥策略的基于属性加密（KP-ABE，key-policy attribute-based encryption）[5]和密文策略的基于属性加密（CP-ABE，ciphertext-policy attribute-based encryption）[6]两大分支，都可用于基于属性的细粒度访问控制。文献[7]将属性加密应用到文件级的密文数据去重，上传者无须提前获知待共享数据用户的身份即可通过属性值来达到秘密共享数据的目的。文献[8]表明，线性访问结构中的密文和加密时间随访问结构的增大呈线性增长，而在树形访问结构中呈指数型增长。线性访问结构与树形访问结构可相互转化。在数据去重中，访问结构大小与用户量相关，因此本文采用线性秘密共享方案（LSSS，linear secret sharing scheme）[9]。

云服务器通过标签进行重复性检测，但若攻击者截获标签，则可冒充文件拥有者。因此在去重操作前，需对用户进行所有权证明（PoW，proof of ownership）[10]，在文件上传时建立默克尔树（MT，Merkle tree）存储于云服务器，仅需与客户交互少量信息即可证明用户是文件拥有者。服务器中的数据是动态变化的，文献[11]实现对动态数据更便捷的所有权证明。

由于当访问结构发生变化时，加密后的密文会发生变化，使用代理重加密[12]可以在原密文上生成新的密文，不需要解密再加密，而引入代理加密和代理解密，在云服务器上进行大部分复杂计算，可以减小用户客户端的计算时间开销[13]。

尽管已有支持去重的ABE方案，但数据块级的基于ABE的数据去重较为少见。本文提出了一种基于线性秘密共享的块级云数据去重方案。该方案将线性秘密共享嵌入块级去重算法，支持文件级和数据块级的双粒度去重，并实现数据块级的数据共享；支持对用户进行所有权证明，引入代理重加密实现更高效的访问结构更新，引入代理加解密减轻客户端的计算负担；在进行所有权证明时，用私有云本身存储的块级标签建立默克尔树对用户发起所有权证明，可节省存储开销。经仿真测试，该方案可提升去重效率，并节省计算时间开销。

1 预备知识

本节介绍几项重要的基础知识：双线性映射是标签一致性检测的重要方式，也应用于密文设计；LSSS访问结构的定义和性质；建立默克尔树是本文所有权证明的方式。决策（-1）假设是安全性证明时用到的重要假设。

1.1 双线性映射

1.2 LSSS访问结构

1.3 默克尔树

默克尔树[15]是一棵存储hash值的树。将文件划分为多个数据块，每个叶子节点存储每个数据块的hash值，非叶子节点存储其子节点串联字符串再进行hash运算的值。默克尔树可用于数据的对比和验证，实现可证明拥有。

可证明拥有由以下步骤组成：初始化、生成挑战信息、生成响应信息和验证响应信息。具体的实现过程如下。

1) 初始化：验证者生成验证数据。

3) 生成响应信息：用户收到验证者发送的挑战信息之后，生成响应信息。

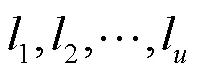
1.4 决策（q-1）假设

对于任何基于概率的多项式时间的算法，给定

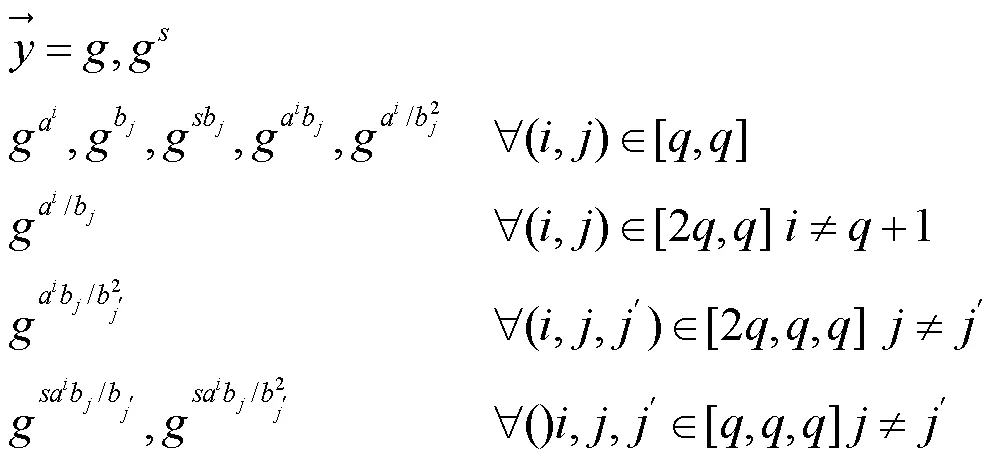
2 属性加密块级去重方案

本节提出一种基于线性秘密共享的数据块级去重方案。

2.1 系统模型

基于LSSS的块级去重系统模型如图1所示，主要由以下三方构成。

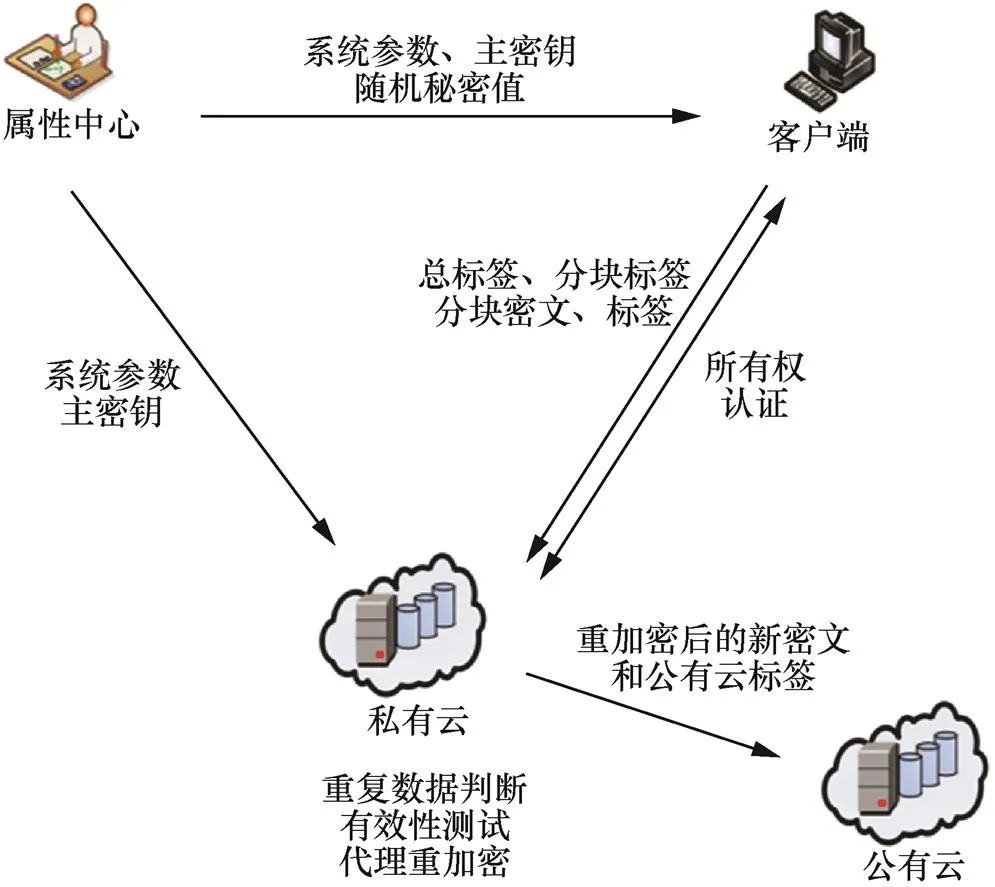
图1 基于LSSS的块级去重系统模型

Figure 1 Block-level deduplication system model based on LSSS

1) 属性中心（AA，attribute authority）

第三方可信机构，为系统生成系统参数、主密钥和公钥。为拥有访问权限的用户生成属性私钥，用户可与云服务器计算得到其有访问权限的数据的明文。

2) 客户端：包括第一位数据上传者和其他用户。

客户端借助云服务器实现数据备份和存储，并将复杂的计算外包给云服务器。属性中心为用户分配与其访问权限相关的属性，使拥有权限的用户可通过分配到的属性访问其有权访问的数据。

3) 云存储服务器：包含公有云和私有云。私有云验证用户对文件是否拥有所有权，负责加解密和重加密计算，拒绝客户重复上传服务器中已存储的数据，并将密文等数据上传至公有云。公有云负责存储大量密文数据。在同一服务器范围内，数据具有唯一性。

在用户上传新文件时，先在用户端通过比较文件级标签，检验文件是否重复。若文件重复，则在通过所有权证明后进行文件级的去重，该步骤直接在客户端进行，无须上传服务器；若文件不重复，则将文件划分成固定大小的数据块，对分块后的数据进行块级去重。此时，属性中心生成属性集、主密钥、公共参数和私钥发送给用户，用户加密不重复的数据块并上传到私有云，私有云对该加密数据进行有效性测试和一致性测试，并将通过测试的块密文存储至公有云。对于公有云上的数据，另外建立一个标签表来查找数据。对于重复的数据块，用户无须再次上传，系统通过属性加密分配给该用户权限，属性中心生成代理密钥发送给私有云，使私有云代理重加密解密出一个中间值，再由私有云发送给用户，由该拥有权限的用户解密出明文。

2.2 方案详细设计

基于线性秘密共享的块级云数据密文去重方案由以下多项式时间算法组成。

2.2.1 初始化阶段

该算法由属性中心运行，生成系统公共参数和主密钥，为系统初始化设置。

2.2.2 文件上传阶段

该算法由客户端运行，先生成文件级标签、数据块标签，发送给私有云，由私有云检索标签列表并进行一致性检验，判断该用户是否为第一位数据上传者。若该用户是数据上传者，则继续计算数据块密文发送给私有云。

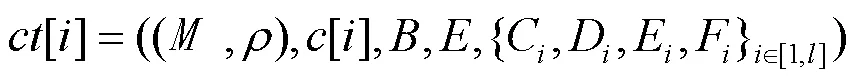
（2）数据块密文相等性检验

该算法由私有云运行。若私有云发现相同标签，则用两数据块对应的文件级标签再次验证两数据块密文是否相等。若相等，则可拒绝上传重复数据。

（3）数据块标签与密文的一致性检验

该算法由私有云运行，验证数据块标签与密文是否一致。

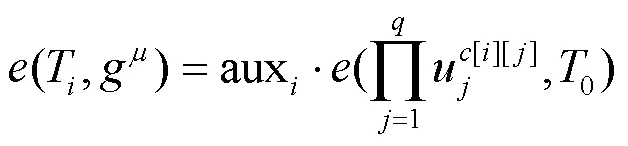
若成立，则可通过一致性验证。

（4）所有权证明

当数据不重复上传至服务器时，属性中心生成代理密钥，并将代理密钥发送给私有云。

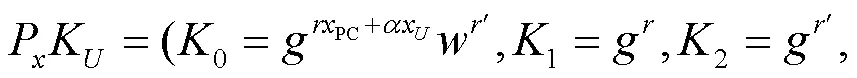
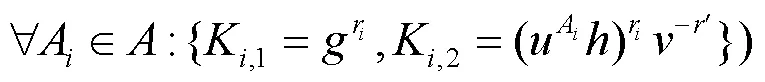
对于新加入的数据拥有者，更新属性列表，则密文需要改变。对私有云上的数据进行代理重加密，使数据不需要解密再加密，实现更为方便的数据共享。

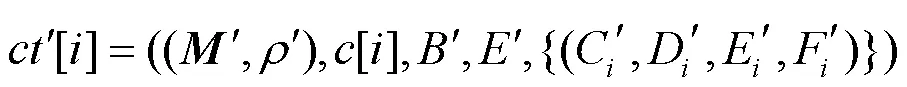
2.2.3 解密阶段

块级去重解密阶段如图2所示，拥有访问权限的用户向AA提出下载请求，AA计算代理密钥并发送给私有云，由私有云解密出中间值再由用户解密出明文。

对于有数据访问权限的用户，从服务器上下载数据时，需要由私有云进行代理解密。

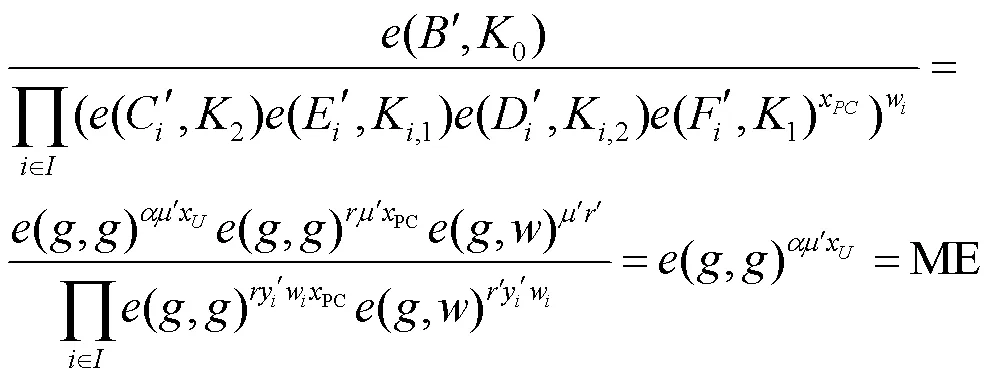
私有云解出一个中间值ME，没有用户的私钥不能继续解密，保护了数据的安全性。

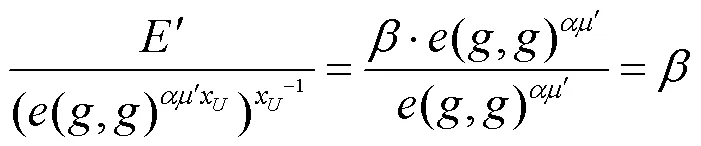
如图2所示，解密阶段私有云代理解密，承担了大部分计算量，且仅有用户可得到明文。

图2 块级去重解密阶段

Figure 2 Block- level deduplication decryption phase

3 安全性分析

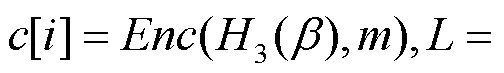
证明

PRV-CDA安全性由加密安全性和重加密安全性构成。加密安全性同定理1，只需考虑添加的部分不会暴露原来关于的信息，其他的证明可以参照Rouselakis-Waters方案的证明。

在考虑到重加密安全性时，需要回顾本文重加密方案的过程。假设有某个攻击者算法破坏了PRV-CDA安全性，本文将构造出一个挑战者算法解决BDH问题，以此来导出矛盾。

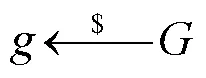
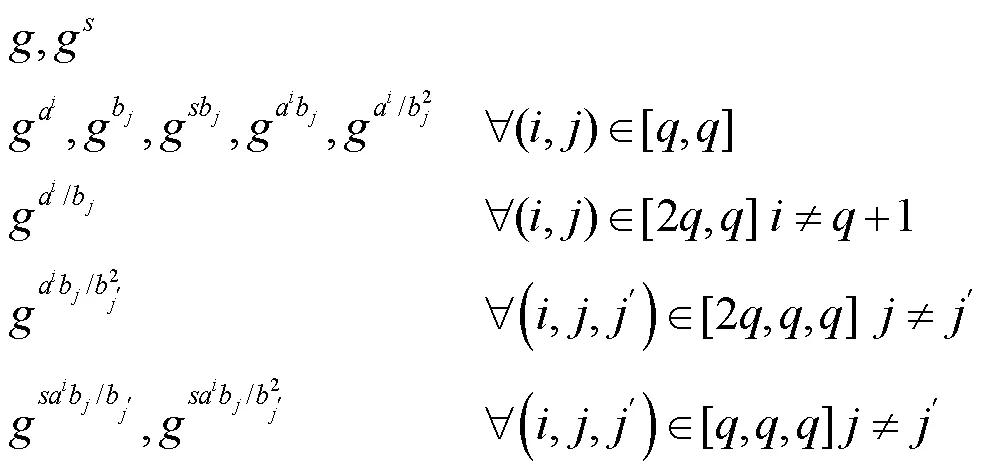
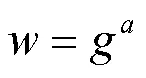
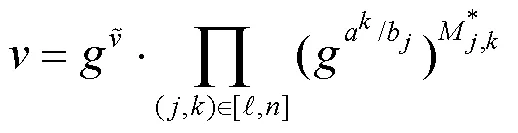
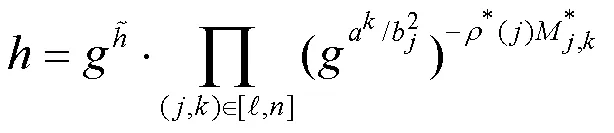
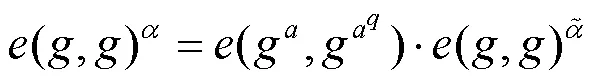
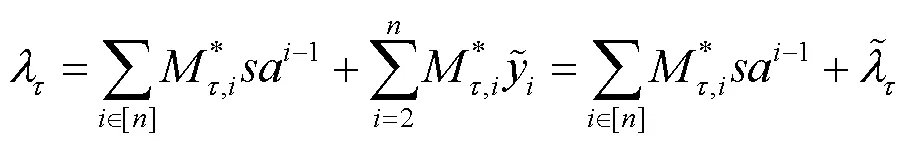
证毕。

4 仿真实验与性能评估

本节给出对本文方案的运行性能评估，选取SS512、MNT159、MNT201、MNT224这4种椭圆曲线，对本文提出的基于属性加密的块级去重方案，分别测试固定分块的算法运行时间，以及各方案对于不同大小的分块的运行时间。

4.1 实验环境

1) 硬件环境

CPU：AMD Ryzen 5 4600H, Radeon Graphics 3.00 GHz

内存：16 GB RAM SAMSUNG

硬盘：512 GB SSD SAMSUNG2

2) 开发环境

开发操作系统：Ubuntu 16.04（64 bit）

开发语言及工具：Python 3.5、GMP-6.2.0库、PBC-0.5.14库、Charm-0.50库、Pycharm、VMware。

4.2 仿真结果

4.2.1 固定分块大小对不同属性个数的计算时间

选取SS512、MNT159、MNT201、MNT224这4种椭圆曲线对固定分块大小为1 kB的基于属性加密的块级去重方案测试运行时间，如图3所示。这4种曲线分别对应112 bit、80 bit、80 bit和100 bit的安全性。

实验结果显示，当属性个数增加时，密钥生成、加密、重加密和解密的计算时间线性增长。这与LSSS的特性相符合。在加解密和重加密的计算中，SS512拥有最小的计算时间开销，而MNT224的计算时间开销最大。在密钥生成算法中，SS512的计算时间开销最大，但对于100个属性个数也仅占用360 ms，相比加密解密和重加密有较大的时间消耗，SS512依然是最优的方法。由实验结果可知，对于固定1 kB的分块，在属性个数为100的情况下，对于最耗时的加密和重加密过程，可将计算时间控制在1.05 s内，对比文献[7]的文件级去重的实验结果，块级的去重方案可节省对于每个分块的计算时间开销。

4.2.2 相同属性个数对不同分块大小的运行时间

对于固定的40个属性，选取SS512、MNT159、MNT201和MNT224这4种椭圆曲线对分块大小为1 MB到30 MB的数据分块，运行本文算法并测试运行时间，实验结果如图4所示。

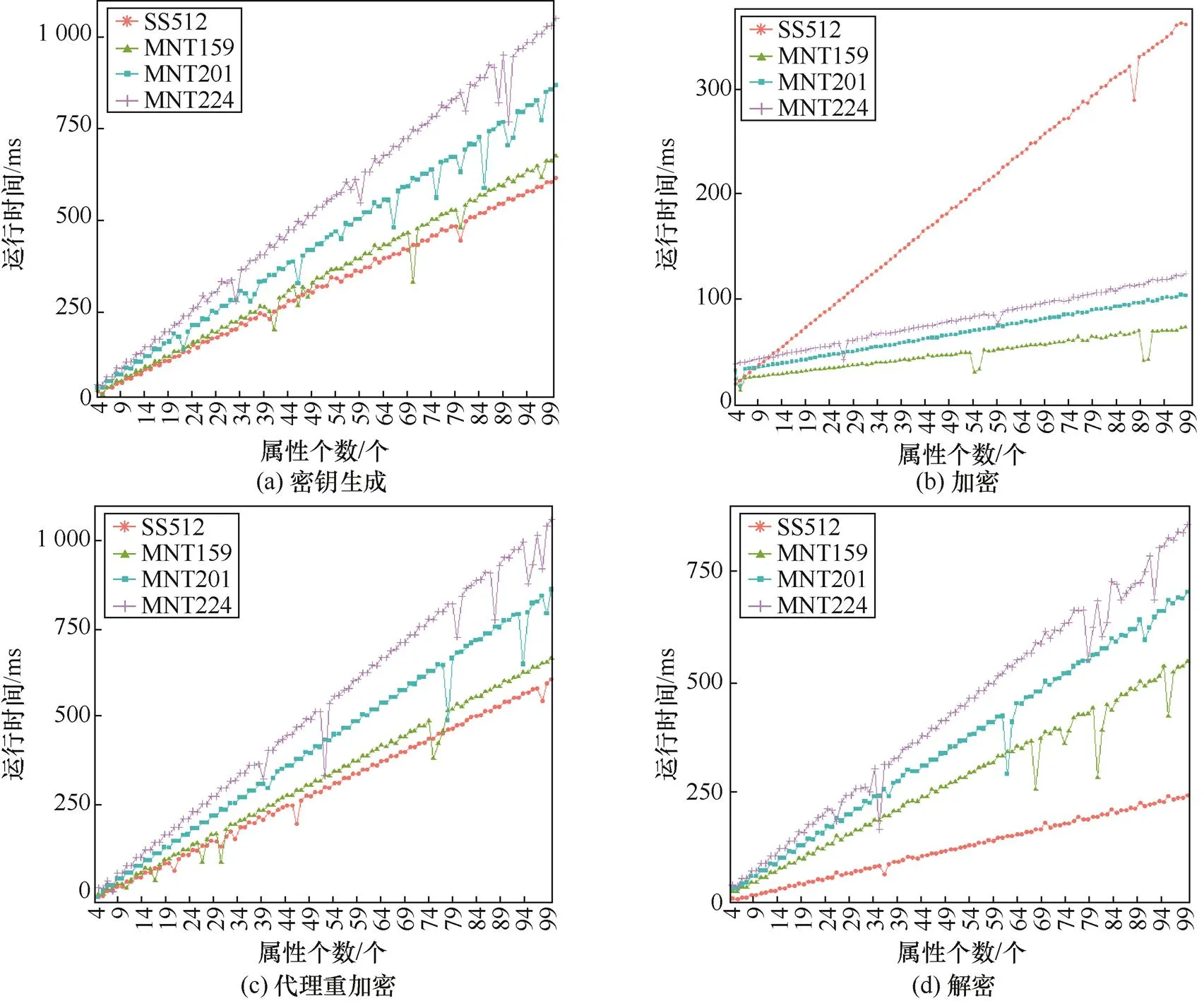
图3 固定分块大小对不同属性个数的运行时间

Figure 3 Fixed block size running time for different number of attributes

图4 相同属性个数对不同分块大小的运行时间

Figure 4 Fixed number of attributes running time for different block sizes

当属性个数固定、分块大小增加时，密钥生成算法不受分块大小的影响，加密和解密算法的运行时间随分块大小的增加呈线性增长，这同样与LSSS的特性相符合。在密钥生成算法中，SS512的运行时间最大，对于固定的40个属性，运行时间为148 ms，是可以接受的。在加密和解密算法中，SS512的运行时间最小，MNT224的运行时间最大。

4种椭圆曲线的运行时间随着分块大小的增加，增长速率几乎是一致的。对于40个属性，在加密和解密中，MNT224的运行时间比SS512的运行时间约长200 ms。因此SS512是可以选取的最优方案。

值得注意的是，以上实验曲线中都存在违反整体趋势的“锯齿”。在密钥生成以及加解密时，出于安全性考虑都随机选取了不同的随机数，尤其选择属性参数时引入了随机量，因此总体线性但有随机误差，产生“锯齿”。若实验增大属性间隔可以减轻此类“锯齿”的情况。

4.3 计算时间开销分析

对本文方案的各多项式算法分析计算时间开销，用表示访问结构的属性数量，用表示与私钥关联的属性集的大小，用表示私有云现存的标签数量。用Exp表示一个指数运算，用Pair表示一个双线性配对运算。由前文已知，在计算标签和进行一致性验证时，将数据块文件划分块。本文方案的各多项式算法的计算时间开销如表1所示。

表1 本文方案的各多项式算法的计算时间开销

指数运算主要存在于生成标签和加解密运算，双线性配对主要存在于一致性检验、相等性检验和解密。

相对文件级去重，块级去重不可避免地增加了对数据块分块时额外产生的指数运算，以及在加解密中添加元组时产生的开销。文献[7]实现了基于属性的文件级云数据去重，各方案的计算时间开销对比如表2所示。

对比可知，本文方案的块级去重的额外计算时间开销均匀分配给数据上传者、私有云和需要共享数据的用户。本文方案设计的数据块标签计算方式增加了次指数运算，同时影响到一致性检验，本文方案增加了3次双线性配对运算。由于在密文中增加新的元组，加解密的开销分别增加了次指数运算和2次双线性配对运算。由理论分析和前文的仿真实验可知，这样的开销增加是可以接受的。

表2 各方案的计算时间开销对比

5 结束语

随着互联网时代的快速发展，云计算凭借其高效和经济的特性正在快速增长。云环境下的存储效率和计算时间开销以及安全性，需要兼顾和平衡。

云环境下基于属性的块级云数据去重方案，是在文件级的基于属性的去重基础上，引入了块级去重，实现更细粒度的去重，提高去重效率。而在属性加密基础上的块级去重，提高了数据共享的能力。本文设计了一种用双线性配对验证完成块级去重情况下的标签与密文一致性检验的方案，该方案由多个多项式时间算法组成。块标签可用于建立默克尔树，对用户进行所有权证明。针对块级云数据去重的整个流程中的密钥生成、加密、代理重加密、解密算法，在选取不同椭圆曲线的情况下，分别对固定分块大小的不同数量的属性集，以及固定属性集数量文件的不同分块大小，测试了计算时间开销。实验结果验证了在LSSS属性加密下，加解密的计算时间开销随属性个数或分块大小的增加而线性增长，而生成密钥的计算时间开销只与属性个数有关，随属性个数的增加线性增长。另外，本文还对该方案进行了安全性分析，该方案是PRV-CDA安全的。下一步工作将重点考虑允许用户自定义密钥情况下的去重，以及海量用户块级去重后的数据所属权管理等。

[1] BELLARE M, KEELVEEDH S. Interactive message-locked encryption and secure deduplication[C]//Public-Key cryptography - PKC 2015: 18th ICAR International Conference on Practice and Theory in Public Key Cryptography. 2015: 516-538.

[2] AHAMED N, DURAIPANDIAN N. Secured data storage using deduplication in cloud computing based on elliptic curve cryptography[J]. Tech Science Press, 2022, 41: 83-94.

[3] CHEN R, MU Y, YANG G, et al. BL-MLE: block-level message-locked encryption for secure large file deduplication[J]. IEEE Transactions on Information Forensics & Security, 2015, 10(12): 2643-2652.

[4] ZHAO Y, CHOW S. Updatable block-level message-locked encryption[J]. IEEE Transactions on Dependable and Secure Computing, 2021,18(4): 1620-1631.

[5] GOYAL V, PANDEY O, SAHAI A, et al. Attribute-based encryption for fine-grained access control of encrypted data[C]//Proceedings of the 13th ACM Conference on Computer and Communications Security. 2006: 89-98.

[6] EMURA K, MIYAJI A, OMOTE K, et al. A ciphertext-policy attribute-based encryption scheme with constant ciphertext length[J]. International Journal of Applied Cryptography, 2009, 2(1): 46-59.

[7] CUI H, DENG R, LI Y, et al. Attribute-based storage supporting secure deduplication of encrypted data in cloud[J]. IEEE Transactions on Big Data, 2019, 5(3): 330-342.

[8] GOYAL V, JAIN A, PANDEY O, et al. Bounded ciphertext policy attribute based encryption[C]//35th International Colloquium on Automata, Languages and Programming (ICALP 2008). 2008: 579-591.

[9] WATERS B. Ciphertext-policy attribute-based encryption: an expressive, efficient, and provably secure realization[C]//Public Key Cryptography-PKC 2011. 2011: 53-70.

[10] GONZALEZ-MANZANO L, ORFILA A. An efficient confidentiality-preserving proof of ownership for deduplication[J]. Journal of Network & Computer Applications, 2015, 50(4): 49-59.

[11] HUANG K, ZHANG X S, MU Y, et al. Bidirectional and malleable proof-of-ownership for large file in cloud storage[J]. IEEE Transactions on Cloud Computing, 2021, (99): 1.

[12] CHEN Y, HU Y, ZHU M, et al. Attribute-based keyword search with proxy re-encryption in the cloud[J]. IEICE Transactions on Communications, 2018, (8): 1798-1808.

[13] 刘尚, 郭银章. 云计算多授权中心CP-ABE代理重加密方案[J]. 网络与信息安全学报, 2022, 8(3): 176-188.

LIU S, GUO Y Z. Multi-authority based CP-ABE proxy re-encryption scheme for cloud computing[J]. Chinese Journal of Network and Information Security, 2022, 8(3): 176-188.

[14] BONEH D, FRANKLIN M. Identity-based encryption from the Weil pairing[J]. SIAM Journal on Computing, 2003, 32(3): 586-615.

[15] SZYDLO M, LECTURE NOTES IN COMPUTER SCIENCE 3027. Merkle Tree Traversal in Log Space and Time[C]//2004 International Conference on the Theory and Application of Cryptographic Techniques (EUROCRYPT 2004). 2004: 541-554.

[16] ROUSELAKIS Y, WATERS B. New constructions and proof methods for large universe attribute-based encryption[C]//ACM Sigsac Conference on Computer & Communications Security. 2013: 463-474.

[17] ROUSELAKIS Y, WATERS B. New constructions and proof methods for large universe attribute-based encryption[C]//Sigsac Conference on Computer & Communications Security. 2013.

Block level cloud data deduplication scheme based on attribute encryption

GE Wenting, LI Weihai, YUNenghai

School of Cyber Science and Technology, University of Science and Technology of China, Hefei 230026, China

Due to the existing cloud data deduplication schemes mainly focus on file-level deduplication. A scheme was proposed, based on attribute encryption, to support data block-level weight removal. Double granularity weight removal was performed for both file-level and data block-level, and data sharing was achieved through attribute encryption.The algorithm was designed on the hybrid cloud architectureRepeatability detection and consistency detection were conducted by the private cloud based on file labels and data block labels. A Merkle tree was established based on block-level labels to support user ownership proof.When a user uploaded the cipher text, the private cloud utilized linear secret sharing technology to add access structures and auxiliary information to the cipher text. It also updated the overall cipher text information for new users with permissions. The private cloud served as a proxy for re-encryption and proxy decryption, undertaking most of the calculation when the plaintext cannot be obtained, thereby reducing the computing overhead for users.The processed cipher text and labels were stored in the public cloud and accessed by the private cloud. Security analysis shows that the proposed scheme can achieve PRV-CDA (Privacy Choose-distribution attacks) security in the private cloud. In the simulation experiment, four types of elliptic curve encryption were used to test the calculation time for key generation, encryption, and decryption respectively, for different attribute numbers with a fixed block size, and different block sizes with a fixed attribute number. The results align with the characteristics of linear secret sharing. Simulation experiments and cost analysis demonstrate that the proposed scheme can enhance the efficiency of weight removal and save time costs.

deduplication, cloud storage, attribute-based-encryption, proof of ownership, linear secret sharing scheme

The National Key R&D Program of China (2018YFB0804101)

葛文婷, 李卫海, 俞能海. 基于属性加密的块级云数据去重方案[J]. 网络与信息安全学报, 2023, 9(5): 106-115.

TP393

A

10.11959/j.issn.2096−109x.2023066

葛文婷（1998− ），女，江苏泰州人，中国科学技术大学硕士生，主要研究方向为数据安全。

李卫海（1975− ），男，辽宁大连人，中国科学技术大学副教授，主要研究方向为多媒体内容安全、数据安全。

俞能海（1964− ），男，安徽无为人，中国科学技术大学教授、博士生导师，主要研究方向为视频处理与多媒体通信、信息检索、媒体内容安全、数据安全。

2023−02−17；

2023−05−28

李卫海，whli@ustc.edu.cn

国家重点研发计划（2018YFB0804101）

GE W T, LI W H, YU N H. Block level cloud data deduplication scheme based on attribute encryption[J]. Chinese Journal of Network and Information Security, 2023, 9(5): 106-115.