基于蜻蜓算法的分布式电源并网容量优化配置

潘万宝,余畅文,马小龙 ,刘 练,刘 闯

（1.国网湖北省电力有限公司荆州供电公司，湖北 荆州 434000；2.国网湖北省电力有限公司荆门供电公司，湖北 荆门 448000）

0 引言

在能源危机和环境问题的双重背景下，以可再生能源为主的分布式电源（Distributed Generation，DG）受到了广泛关注[1-2]。光伏、风电等DG 在发电过程中不消耗化石能源，能够源源不断地输出清洁电能，但这些DG 输出功率的波动性较大，在并网时会改变电力系统的潮流大小和方向，给电力系统安全性和稳定性带来一定影响[3-4]。因此，为了减小DG 并网带来的不良影响，合理规划DG 接入位置及容量具有重要意义。

目前，针对DG 并网的选址定容问题，国内外专家学者进行了大量研究。文献[5]提出了一种基于改进蚁狮算法的分布式电源优化配置方法，以功率损耗和电压稳定性为优化目标，采用改进蚁狮算法对多目标函数进行优化，获得了DG 最优配置方案。文献[6]提出了一种兼顾经济性和稳定性的分布式电源配置方法，建立了分布式电源多目标优化配置模型，利用层次分析法计算各指标权重，将多目标转化为单目标，利用改进乌燕鸥算法进行求解，算例分析验证了该方法的有效性。文献[7]首先建立了以DG 投资成本、运维成本、网损成本和用户购电成本之和最小为目标函数的DG 优化配置模型，然后采用对配电网潮流进行计算，并利用自适应遗传算法对模型进行求解，最后利用算例分析验证了所提模型既能够保证配电网运行的经济性，又能提高电压质量。上述方法分别提出了不同的分布式电源配置方法，但均没有对DG接入数量带来的影响进行深入分析，因此针对不同数量DG 并网的优化配置问题有待进一步研究。

1 分布式电源优化配置模型

1.1 目标函数

配电网网损是衡量配电网运行状态的重要指标[8]，DG 并网后会使系统潮流发生变化，从而改变网损，本文以配电网网损最小为目标函数，其数学表达式为：

式中:Ploss为配电网网损；k为配电网中各支路编号；Rk为支路k的电阻；Pk、Qk为支路k的有功功率和无功功率；Qk为支路k的末端电压；m为配电网支路总数。

1.2 约束条件

对分布式电源进行优化配置时，需要考虑功率平衡、节点电压、支路电流及DG 容量等约束，具体如下：

（1）功率平衡约束

式中：i、j均为配电网网络的节点编号；Pi、Qi分别为系统在第i个节点注入的有功功率和无功功率；PDGi、QDGi为DG 在第i个节点注入的有功功率和无功功率；Ui、Uj分别为第i个节点和第j个节点的电压；Gij、Bij分别为第i个节点和第j个节点组成支路的电导和电纳；θij为第i个节点和第j个节点组成支路的电压相角差；PLi、QLi分别为第i个节点的有功负荷和无功负荷。

（2）节点电压约束

式中：Ui.min为第i个节点的最低电压；Ui.max为第i个节点的最高电压。

（3）支路电流约束

式中：为支路k流过的电流；为支路k允许通过的最大电流。

（4）传输功率约束

式中：Pij为第i个节点和第j个节点组成支路的传输功率；Pijmax为该支路允许传输的最大功率。

（5）配电网DG 容量约束

式中：η为DG 占比系数，取值为0.25。

2 蜻蜓算法

蜻蜓算法（Dragonfly Algorithm）是数学家Mirjalili根据蜻蜓自然行为提出的一种群体智能优化算法[9]。在DA 算法中，蜻蜓种群分为静态群体搜索和动态群体搜索，前者是指小群体蜻蜓的整个解空间中的全局搜索行为，后者则是指大群体蜻蜓在小范围内的局部寻优过程，可见DA 算法具有良好的优化性能，目前已在能源、医疗、交通等领域得到了广泛应用[10]。

在DA 算法中，定义邻域半径r的增长与算法的迭代次数成正比，如果两只蜻蜓之间的距离小于邻域半径，则认为两只蜻蜓是相邻的。蜻蜓种群通过分离、队列、凝聚、寻猎和避敌5种行为来实现个体位置的更新，具体如下：

（1）分离

蜻蜓个体在飞行过程中应避免发生碰撞，该过程的表达式为：

式中：Si为第i只蜻蜓的分离量；t为迭代次数；Xi(t)为第t次迭代时第i只蜻蜓的位置；为Xi(t)的第j只临近蜻蜓个体；N为临近蜻蜓个体的总量。

（2）对齐

蜻蜓个体在飞行过程中要与蜻蜓种群中的其他个体相互对齐，该过程的表达式为：

式中：Ai为第i只蜻蜓的对齐量；为第t次迭代时第j只临近蜻蜓个体的速度。

（3）凝聚

蜻蜓个体在飞行过程中会向自己所属的群体靠近，该过程的表达式为：

式中：Ci为第i只蜻蜓的凝聚量。

（4）寻猎

蜻蜓个体在飞行过程中会受到食物的吸引，此时蜻蜓个体会向食物靠拢，食物所在位置即为最优蜻蜓个体的位置，该过程的表达式为：

式中：Fi为第i只蜻蜓在寻找猎物时移动的距离；为第t次迭代时食物的位置。

（5）避敌

蜻蜓个体在飞行过程中尽可能远离天敌，以防止遭受天敌攻击，天敌所在位置即为最差蜻蜓个体的位置，该过程的表达式为：

式中：Ei为第i只蜻蜓在躲避天敌时移动的距离；为第t次迭代时天敌的位置。

蜻蜓的活动方式取决于上述五种行为，因此可以得到蜻蜓的飞行步长为：

式中：ΔXi(t)、ΔXi(t+1)分别为第i只蜻蜓在第t次迭代和第t+1 次迭代时飞行步长；s为分离量权重；a为对齐量权重；c为凝聚量权重；f为寻找食物的权重系数；e为逃避天敌的权重系数；ω为惯性权重。

由此可以得到蜻蜓个体的位置更新公式为：

如果蜻蜓个体周围没有邻近个体，则利用莱维飞行策略进行随机飞行，其表达式为

式中：D 为空间维数，Levy为莱维飞行函数，其表达式为：

式中：r1、r2均为随机数，取值范围为(0,1)；Γ为Gamma 函数；β为常数，取值为1.5。

3 DA算法求解分布式电源优化配置模型

本文采用算法对分布式电源优化配置模型进行求解，主要求解步骤如下，具体流程如图1所示。

图1 DG 优化配置流程图

1）输入DG 个数，初始化相关参数。输入配电网运行数据，对DA 算法的相关参数进行设置，主要包括蜻蜓种群规模的最大迭代次数。

2）初始化蜻蜓个体的位置和蜻蜓飞行步长。

3）更新DA 算法的相关系数，随机初始化相邻半径、各权重量和权重系数。

4）计算适应度值。将目标函数作为适应度函数，计算蜻蜓飞行一次后的适应度值，并选出其中的最优适应度值。

5）判断蜻蜓个体是否存在相邻蜻蜓个体，若是则利用式（13）进行迭代，否则利用式（14）进行迭代；

6）计算蜻蜓个体的行为参数。利用式（7）～（11）分别对分离量权重、对齐量权重、凝聚量权重、寻找食物的权重系数、逃避天敌的权重系数进行计算。

7）更新蜻蜓位置，利用步骤（5）对蜻蜓位置进行更新，同时利用式（12）调整蜻蜓飞行步长。

8）判断算法是否能够继续运行，若已达到最大迭代次数，则输出最优解，否则返回步骤（4）继续迭代。

4 算例分析

采用如图2 所示的IEEE33 节点测试系统进行仿真分析，该系统中共有33个节点，32条支路，其中节点1 为电源点，系统基准电压为12.66 kV，三相基准功率为10 MVA，系统总负荷为5 084.26+j2 547.32kVA，各节点及支路参数可参考文献[11]。

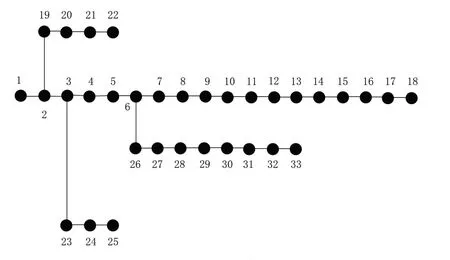
图2 IEEE33 节点系统

DA 算法的相关参数设置为[12]：蜻蜓种群容量N=30、最大迭代次数Tmax=200，分离量权重s=0.2；对齐量权重a=0.2；凝聚量权重c=0.1；寻找食物的权重系数=0.1；逃避天敌的权重系数e=0.25；ω惯性权重ω=0.2。

采用蜻蜓算法对分布式电源优化配置模型进行优化计算，并根据DG 接入个数的不同设置下列三种不同场景进行仿真分析，三种场景下的DG 接入有功容量和无功容量均相同。

（1）场景一：接入1个DG

在IEEE33 节点测试系统接入1 个DG 后的最优配置结果见表1，此时系统电压、各支路损耗和支路电流相比DG 接入前的分布情况分别如图3～图5所示。

表1 四种算法优化重构的收敛曲线

图3 接入1 个DG 前后的系统各节点电压对比

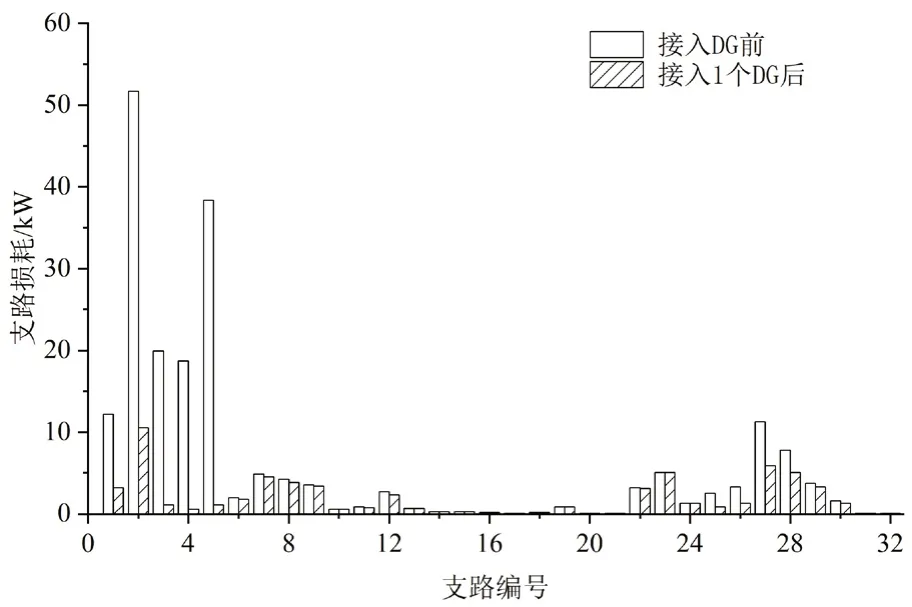
图4 接入1 个DG 前后的系统各支路损耗对比

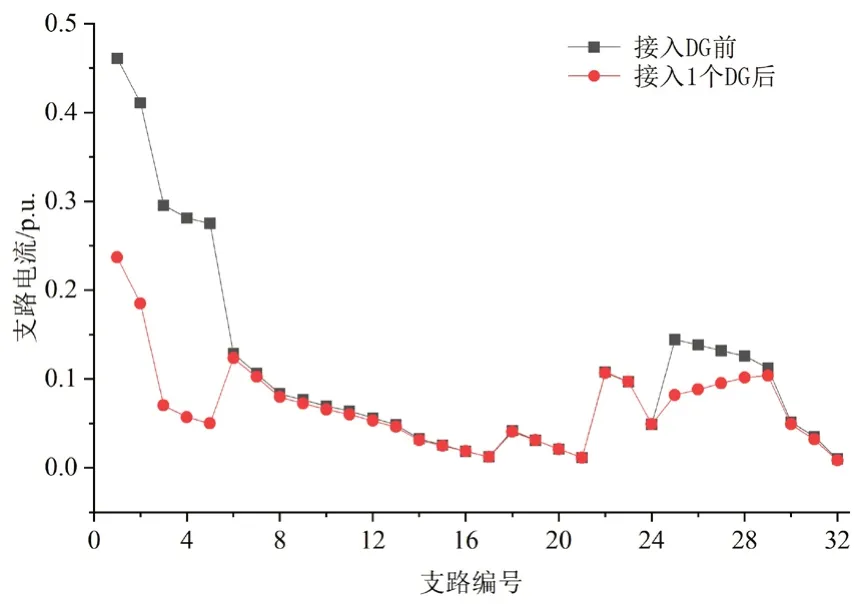
图5 接入1 个DG 前后的系统各支路电流对比

（2）场景二：接入2个DG

在IEEE33 节点测试系统接入2 个DG 后的最优配置结果见表2，此时系统电压、各支路损耗和支路电流相比DG 接入前的分布情况分别如图6～图8所示。

表2 四种算法优化重构的收敛曲线

图7 接入2 个DG 前后的系统各支路损耗对比

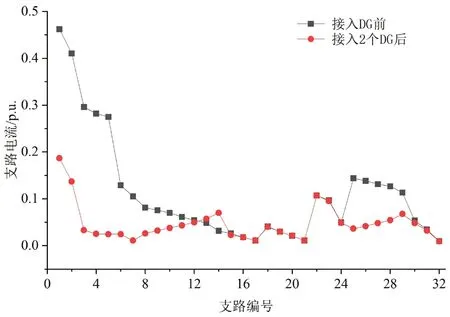
图8 接入2 个DG 前后的系统各支路电流对比

（3）场景三：接入3个DG

在IEEE33 节点测试系统接入3 个DG 后的最优配置结果见表3，此时系统电压、各支路损耗和支路电流相比DG 接入前的分布情况分别如图9～图11所示。

表3 四种算法优化重构的收敛曲线

图9 接入3 个DG 前后的系统各节点电压对比

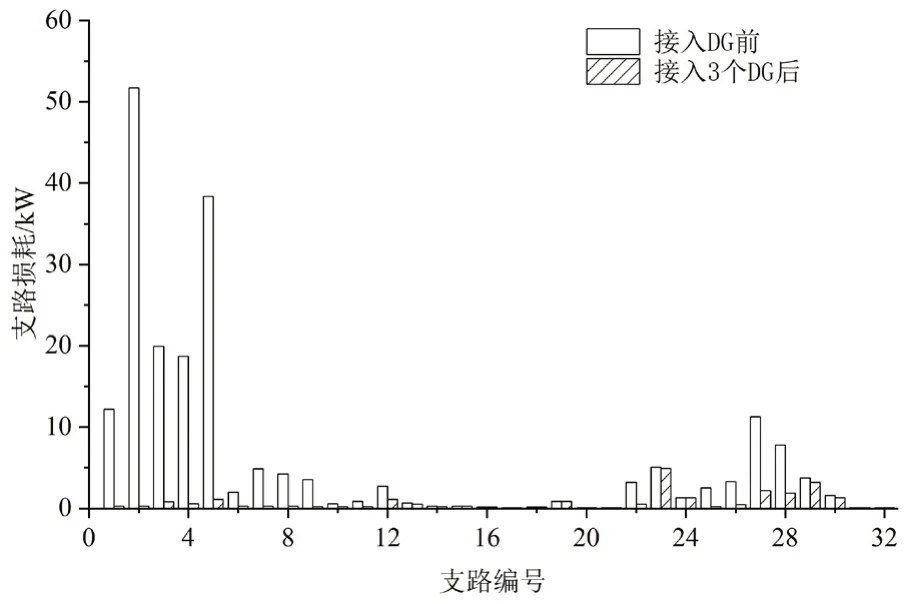
图10 接入3 个DG 前后的系统各支路损耗对比

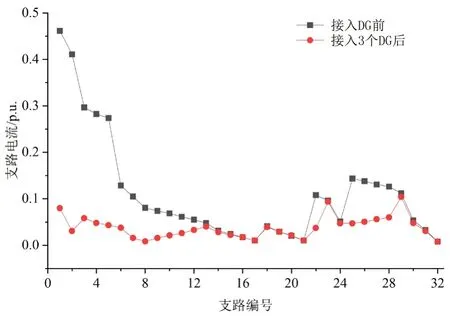
图11 接入3 个DG 前后的系统各支路电流对比

在接入容量一定时，三种不同场景下DG 接入后的网损情况见表4。由表4 可知，在配电网中配置一定数量的DG 后，配电网网损明显降低，且随着接入DG 个数的增加，配电网网损进一步减小，可见光伏分散式接入更加有利于降低系统网络损耗。

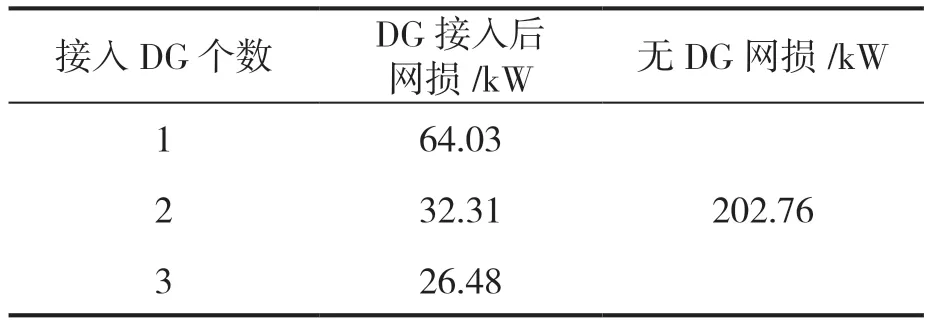
表4 三种场景优化结果对比

在场景三的基础上，对满足DG 接入容量约束下的最小网损进行计算，DG 配置结果见表5。由表5 可知，在配电网中按照表5 中的方案接入DG 时，配电网系统的网损最小，最小网损为22.89 kW，相比DG 接入前，配电网网损降幅高达88.71%。综上所述，在配电网中合理配置DG，能够使配电网系统的各支路损耗明显降低，各支路电流分布更加均衡，配电网运行的经济性和稳定性更好，验证了本文所提分布式电源优化配置方法的正确性。

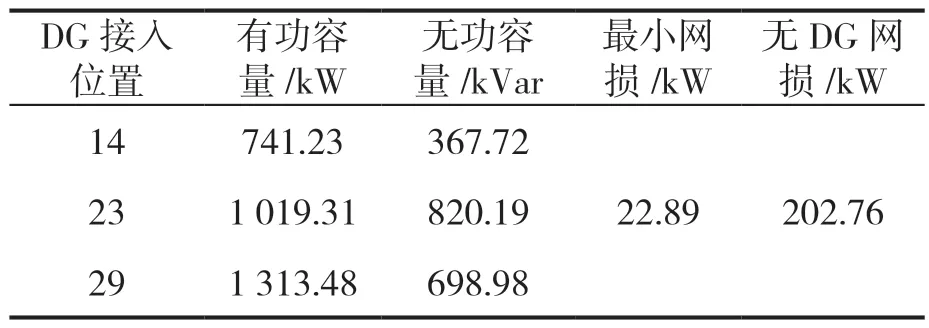
表5 网损最小时的DG 配置方案

5 结论

本文以配电网网损最小为目标函数，建立了基于蜻蜓算法的分布式电源优化配置模型，根据DG 接入数量的不同设置三种场景进行仿真分析，采用蜻蜓算法对目标函数进行优化，仿真结果表明，在配电网中配置一定数量的DG 后，配电网网损明显降低，且随着接入DG 个数的增加，配电网网损进一步减小，当系统配置3 个DG 时的优化效果更好，此时系统节点电压波动更小，各支路损耗最低，且支路电流分布更均衡，配电网运行的经济性和稳定性更好。