含阶梯水电站的多能联合发电系统低碳优化调度
潘福亮
(百色新铝电力有限公司,广西 百色 533000)
0 引言
构建以新能源为主的新型电力系统是实现“双碳”目标的主要途径之一。随着火电机组占比幅度降低,电网调节容量也随之降低,系统的调峰将面临严峻挑战,同时给新能源消纳带来困难,因此需要寻找一种容量较大且调节成本较低的电源作为系统的调峰电源以提高新能源消纳率[1-2]。文献[3]以提高新能源消纳率和实现削峰填谷的原则,提出了储能配置规模的优化模型。文献[4]提出了一种考虑新能源随机性及电网N-1 安全约束的风-光-储协同规划方法,以实现新能源高渗透率下储能的优化配置。针对抽水蓄能电站作为电力系统调峰资源已有较多研究,文献[5]利用自适应粒子群算法确定抽水蓄能电站发电计划以平抑新能源波动给电网带来的调峰困难;文献[6]建立了风-光-水-蓄联合优化调度模型,通过多能互补实现新能源高效利用。化学储能因为成本高昂,也无法大规模应用于电网调峰,抽水蓄能电站虽然技术成熟但受限于库容调节容量有限,因此对电网调峰贡献也有限。
阶梯水电站规模大,调节灵活,利用流域内阶梯水电站参与大规模新能源消纳调节具有重要意义。目前已有许多学者针对阶梯水电站参与电力系统调峰课题进行研究,但相关研究涉及阶梯水电站调度周期内发电量最大以及新能源消纳率最高较多。文献[7]以水电站发电量最大为目标,并考虑水电机组对火电机组深度调峰的影响,同时优化水电机组和火电机组的出力;文献[8]基于阶梯水电站兼具发电和储能的功能,结合风-光-水-火互补特性,建立多能源互补调节的优化调度模型,提高阶梯水电站的发电量。虽然阶梯水电站参与系统调峰能够有效提高新能源消纳率,但调节过程中火电机组的碳排放同样不容忽视,当前的多能源发电系统中多以经济性最优和消纳率最大为目标。然而,在“双碳”目标下,不得不考虑火电机组的碳排放压力,文献[9]从经济性和环保两方面把发电成本、碳排放成本、弃风弃光惩罚成本之和最小作为目标,建立了含抽水蓄能的混合系统优化调度模型,以达到资源优化配置的目的。文献[10]以系统投资成本最小为上层目标,以售电收益最大为下层目标,构建了光伏/水电/抽水蓄能容量配置双层优化模型,但该文献没有考虑火电机组的碳排放成本。
基于已有的研究基础,本文对火电机组调峰和阶梯水电站调峰进行协调优化,从经济性、碳排放、净负荷(系统原始负荷功率减去上网的新能源功率后剩余的负荷定义为净负荷)波动3 个方面构建了发电系统多目标优化模型,以某一市级电网为算例,利用非支配排序遗传算法(NSGA-Ⅱ)对多目标规划模型求解,并根据主观权值修正的熵权双基点法从Pareto 最优解集获得综合最优解。
1 基于梯级水电调节的多能联合发电系统低碳优化调度模型
本节从系统运行经济性、碳排量、平抑净负荷波动效果三方面,构建含阶梯水电站的多能源联合发电系统多目标优化模型。
1.1 目标函数1
多能联合发电系统的运行成本包括火电机组燃料成本、各电厂维护成本、弃风弃光成本,如式(1)所示。
式中:N为区域电网火电机组数量,T=24 表示将一天划分为24 个时段;ai,bi,ci为机组i的煤耗系数,Pgi,t为机组i在时段t的出力;2)Cm为各发电设备维护费用:
1)其中,Cg为火电机组燃料成本:
式中:Cfp、Chp、Cwt、Cpv、分别代表火电机组、阶梯水电机组、风电集群、光伏集群运维成本系数,设置火电机组、水电机组、风电集群和光伏集群的运维成本系数分别为0.01 元/kWh、0.003 元/kWh、0.004 元/kWh、0.002 元/kWh;代表水电机组j在t时段的出力,Nh为水电机组数量,Pw,t代表风电集群在t时段的出力,Pv,t代表光伏集群在t时段的出力。
3)弃风弃光成本:
式中:ω为弃风弃光惩罚系数,P′wt,t、P′pv,t分别为t时段风电集群和光伏集群的弃风量和弃光量。
1.2 目标函数2
目标函数2 以系统火电机组碳排放量最小为目标:
式中:E为火电机组总碳排放,λ1、λ2、λ3为机组碳排放系数。
1.3 目标函数3
目标函数3 以阶梯水电平抑系统净负荷波动为目标,系统净负荷波动以净负荷方差表示,如式(6)所示。
目标函数3 以平抑系统负荷波动为目标,将系统原负荷与光伏出力、风电出力相叠加的峰谷方差(只取数值参与计算,所以本文定义的方差没有单位)最小为目标,如下式:
式中:PL,t为系统在t时段原始预测负荷,PL 为一个调度周期内原始预测负荷的平均值,另外,本文为了便于讨论,将原预测负荷曲线加上光伏、风电上网功率曲线定义为系统等效负荷曲线。
1.4 约束条件
约束条件包括系统的发供电平衡约束,火电机组运行约束,阶梯水电站运行约束等。
1)系统发供电平衡约束
2)火电机组运行约束
火电机组的运行约束包括发电机组的出力上下限约束、爬坡约束,由于本文研究的调度时段为24 小时,很少有火电机组在一天内启停参与电网调节,所以不考虑火电机组启停约束条件:
3)阶梯水电站运行约束
水轮发电机出力特性约束:
4)阶梯水电站库容和流量约束:
①水量平衡约束
式中:Vj,t、Vj,t+1表示t、t+1 时段水库的水量,qj,t、Qj,t为t时段的入库流量和发电流量。
②水位约束
式中:Zj,max、Zj,min分别表示水库水位的上下限。
③发电流量约束
式中:Qj,max、Qj,min分别表示出库流量上下限。
2 NSGA-II算法原理及其改进
NSGA-II 算法首先随机生成N个父代种群,随后利用非支配排序法对父代种群进行排序,然后通过计算个体的拥挤度决定个体所在的层级,根据选择算子选出合适的个体放入交配池,并对放入交配池中的个体进行交叉、变异以产生下一代个体;最后利用精英策略,淘汰不达标的个体,让优秀个体进入下一代优化,通过多次迭代获得Pareto前沿。
2.1 基于正态分布交叉算子的NSGA-II 算法改进
在计算个体拥挤度以决定个体所在层级过程中,某一个个体的拥挤度由其前后两个个体的差值决定,导致传统NSGA-II 算法受限于采用二进制交叉算子产生子代,导致算法容易陷于局部最优解和算法不稳定。为了增强NSGAII 算法跳出局部最优解的能力以弥补算法缺陷,本文在算法变异步骤加入正态分布交叉算子,以增强算法全局搜索能力,提高迭代收敛速度。具体改进步骤如下:将随机生成的N个父代种群分为P1、P2,利用正态分布交叉算子产生子代种群Q1、Q2的计算公式如式(16)~(17)所示:
随机产生一个随机数r,0<r≤1,当r≤0.5时:
其中,N(0,1)为标准正态分布。改进后的NSGA-II 算法流程图如图1所示。
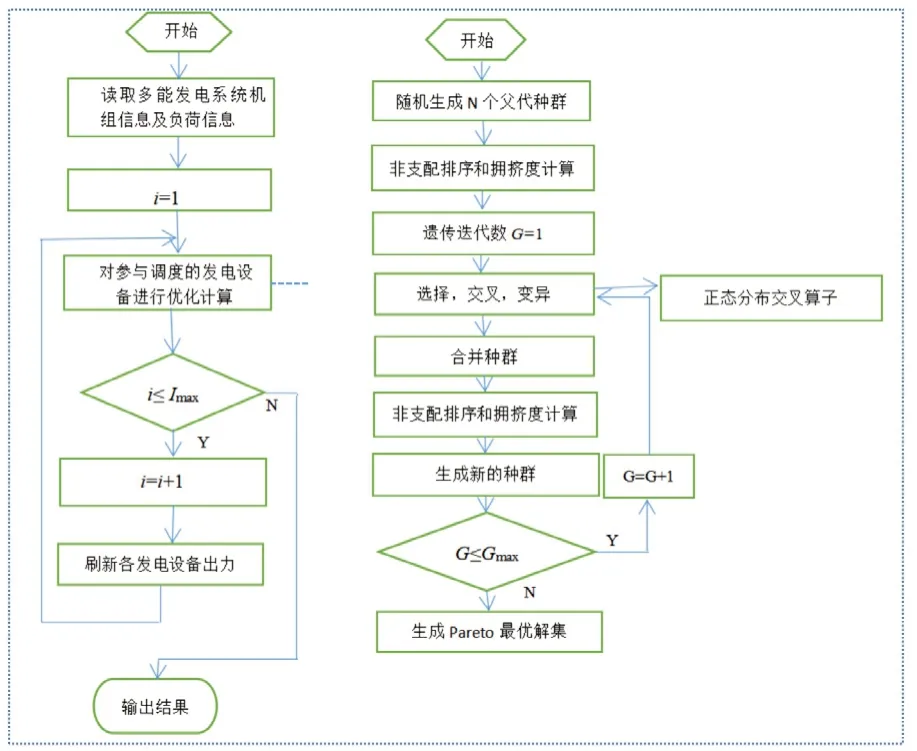
图1 NSGA-II 算法计算流程图
3 多目标决策
利用NSGA-II 算法求解多目标优化模型得到的是一组最优解集,但是系统中每一个设备在某一时间段只有一个运行状态,因此需要一种算法帮助运行人员从最优解集中选出一个折中最优解。为了保证折中最优解具有较强的理论依据,本文选择利用基于主观权值修正的熵权双基点法为调度员从最优解集中选择折中最优解,具体步骤如下:
建立评价矩阵。评价矩阵用于评价Pareto最优解集中最优解的差异程度,本文的优化模型有3 个目标函数,可建立如下评价矩阵R。
式中:M为Pareto 最优解集中最优解个数,表示第i个目标函数的第j个Pareto 最优解。
计算各个目标函数的熵权值α=(α1,α2,α3)T。熵权值体现的是不同最优解之间的差异,可以用来表示多目标优化模型中不同目标函数对最优解影响的大小。计算公式如下:
根据运行人员的主观意识权值βi,i=1,2,3,求修正权系数:
由上式可以看出,修正系数ωi既反应了Pareto 最优解集中最优解之间的差异,又包含了运行人员的主观经验。
建立评价矩阵
上式中矩阵第i行的最大值和最小值对应第i个目标函数的最理想和最不理想情况。
确定双基点
①正理想点。正理想点定义为式(22)的集合点:
②负理想点。负理想点定义为式(23)的集合点:
计算Pareto 最优解集中最优解的相对贴近度TJj:
由此,可以利用基于主观权值修正的熵权双基点法从Pareto 最优解集中选择折中最优解既,考虑了运行人员的个人经验又体现了不同目标函数的重要性,是一种较可靠的决策方法。
4 算例分析
为验证上文提出的多目标优化模型的有效性,以某市级电网的典型运行方式数据为例进行验证分析。该电网装机容量为6 300 MW,其中火电装机容量4 800 MW,水电站装机容量900 MW,新能源装机容量600 MW。系统接线图如图2 所示,系统典型负荷曲线如图3 所示,系统其它参数详见文献[11]。
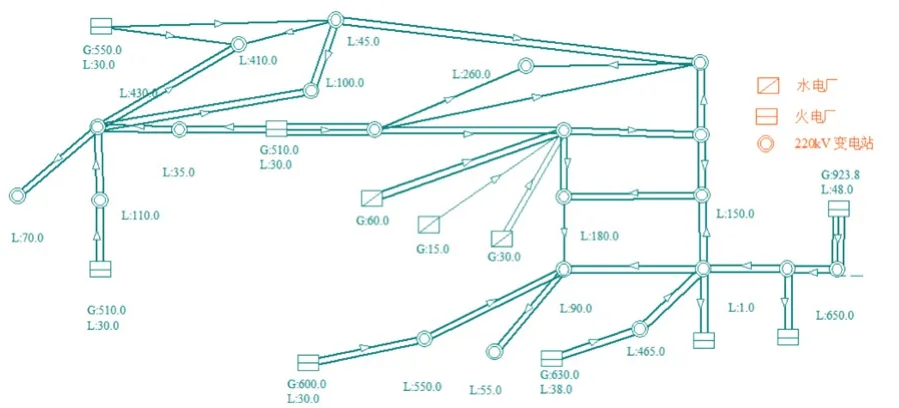
图2 某市级电网系统接线图
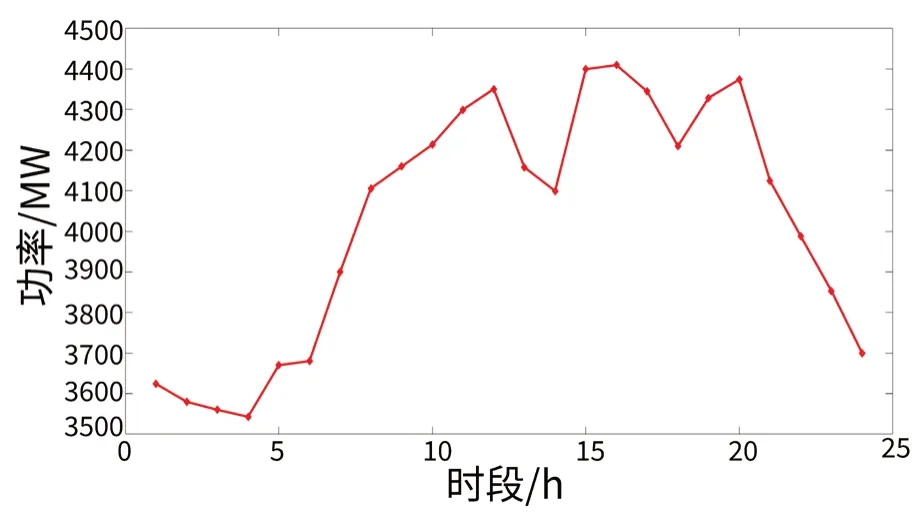
图3 典型负荷曲线
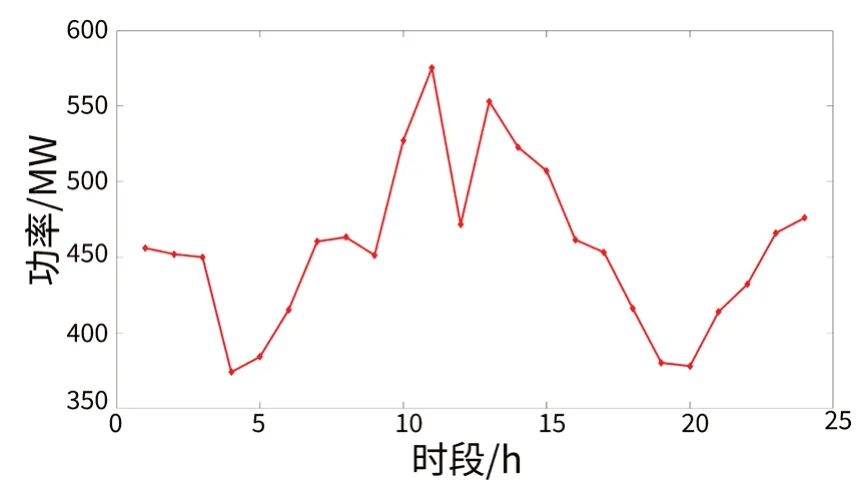
图4 新能源出力曲线
4.1 Pareto 前沿分析
系统典型运行方式下利用NSGA-Ⅱ求得的含阶梯水电站的多能发电系统的3 目标优化Pareto 前沿如图5 所示,3 个端点见表1。
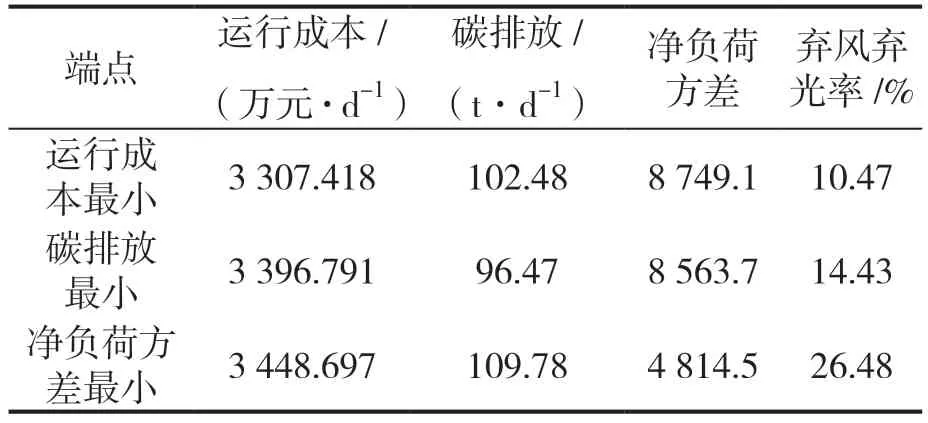
表1 Pareto 端点
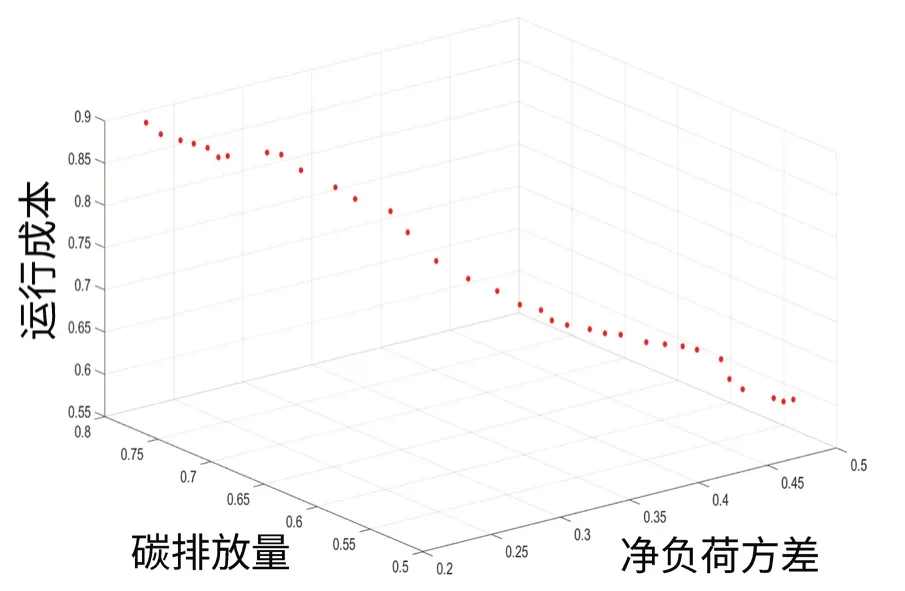
图5 Pareto 前沿
由于光伏、风电等新能源发电过程中不消耗燃料,因此当以降低系统运行成本或减少碳排放为目标时,系统将消纳更多的新能源电量,导致系统净负荷方差变大,但此时弃风弃光率较低;若以追求系统平稳运行,即负荷净方差偏差小为目标,则系统消纳的新能源比例将减小,而且系统运行成本和碳排放将增加。
4.2 熵权双基点法决策效果分析
根据第3 节分析,运行人员可以根据自身经验通过主观权值β来选取折中最优解。本文选取β= (1/3,1/3,1/3),通过式(20)计算得到的修正权系数ωi,见表2。从表中可以看出,运行成本能够导致Pareto 最优解集中的解差异最大,因此在上文建立的3 个目标优化模型中运行成本对折中最优解的影响最大,因而折中最优解应该是系统运行成本较低的点。

表2 各目标函数的修正权系数
对Pareto 最优解集进行优劣排序,并选取Pareto 最优解集中相对贴近度最大的解作为折中最优解,最优解见表3。将表3结果和表2作对比,折中最优解系统运行成本3 423.324 万元,比最小运行成本3 307.418 万元,增加2.87%;折中最优解碳排放量105.87 t,比最小碳排放量96.47t,增加8.87%;净负荷方差5 046.5 比最小净负荷方差4 814.5,增加4.82%。可以看出折中最优解的目标函数值与理想的乌托邦点距离较近,是Pareto 最优解集中质量较好的点。

表3 折中最优解对应的目标函数值
4.3 阶梯水电站对系统运行影响分析
为对比分析阶梯水电站对系统经济低碳运行的影响设置2 个场景,负荷为图3 所示典型负荷。
场景1:阶梯水电站没有参与系统调节;
场景2:阶梯水电站参与系统优化调节。
表4 给出了不同场景下净负荷峰谷差和负荷波动方差。图6 为不同场景下净负荷曲线。从表4 和图6 的计算结果可以看出,在场景1情况下,新能源的接入导致净负荷峰谷差较大,净负荷方差也较大;在场景2 中通过阶梯水电站的平抑作用净负荷最大峰谷差由619 MW 降至485 MW,净负荷方差由1 1287 降至5 536,阶梯水电站的平抑效果明显;另外,场景2 净负荷曲线比场景1 下降较多,表明阶梯水电站参与优化后系统消纳更多的新能源。

表4 梯级水电调节前后的净负荷特性对比
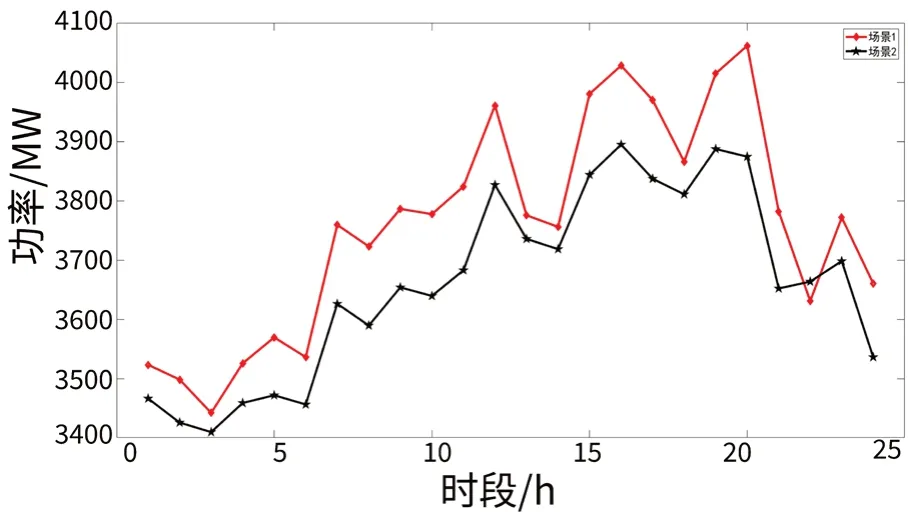
图6 阶梯水电站对新能源波动抑制效果
在折中最优解处,阶梯水电站的在不同场景下的总出力如图7 所示。可以看出,场景1 下,阶梯水电站出力比较平稳,仅和负荷变化趋势存在一定关联;但在场景2 下将阶梯水电站纳入系统调节量后,水电站出力同时和负荷变化及新能源出力存在关联,整体上在场景2 模式下阶梯水电站总出力较场景1 模式下低,并且当新能源出力低时或负荷峰时段水电站增加出力,反之则降低出力,使系统接纳更多新能源电量。
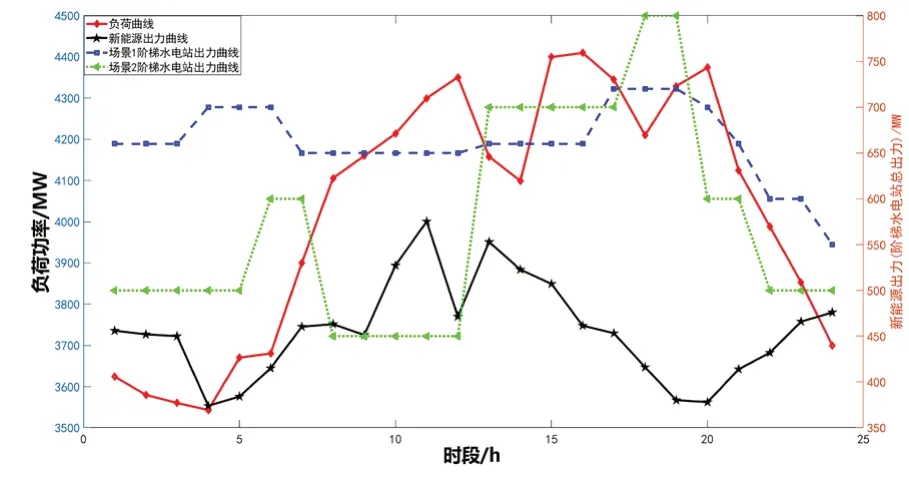
图7 不同场景下阶梯水电站总出力曲线
5 结语
本文讨论了阶梯水电站参与电力系统低碳优化运行问题,得到以下结论:
1)阶梯水电站参与系统低碳优化运行后,系统运行经济性和环保性得到改善,净负荷波动和水资源消耗量下降,验证了算法和模型的有效性;
2)基于熵权双基点法选取的折中最优解包含目标函数价值信息和运行人员经验,是质量较高的最优解,能够有效提高系统综合经济效益;
3)引入正态分布算子后NSGA-II 算法能够获得较为均匀分布的Pareto 前沿,为运行人员提供提供较为完整和准确的决策信息。

