基于双层模糊控制模型的混合储能控制参数优化研究

周 旺，张 波，樊国旗，赵禹来，黄晓峰，吴胥阳

（国网浙江省电力有限公司金华供电公司，浙江 金华 321017）

0 引言

近年来，随着风电等可再生能源在电网中比例不断增加，为了改善其出力不确定性给电网安全稳定运行带来的挑战，混合储能技术得到了广泛的应用研究。混合储能一般由能量型和功率型储能组成，其综合考虑了不同类型储能特点，使得系统整体上在响应速度、短时充放电功率、能量等方面都有较好表现，可以有效改善系统的响应性能，提高其经济性。

混合储能系统设计的关键在于控制策略的制定，而小波包分解在处理风电出力这种时变的非平稳信号方面有较大优势，可以实现混合储能内部功率的合理分配。文献[3-4]依据风电出力的频段分布特点以及储能的响应时间，实现电池和超级电容动态功率分配。文献[5]依据相关标准有功功率波动限值和电池响应速度，确定风电并网功率以及优化混合储能内部出力。文献[6]秉持“能者多劳”的原则，设置根据储能荷电状态变化的分频点。上述研究虽然可以较为简便实现混合储能功率分配，但是对于影响控制效率的小波包分解层数、频段划分等参数的判断多基于经验总结，缺乏定量分析，存在一定的局限性。

文献[7]基于储能寿命量化模型，通过合理选择混合储能协调控制参数来延长锂电池使用寿命。文献[8-9]基于小波包分解和双层模糊控制，通过对储能荷电状态的判断调整储能出力。文献[10]采用粒子群算法确定VMD 算法中K 值（分解模态数）和α 值（二次惩罚因子）的最优值组合，实现储能系统荷电状态的优化调整。上述研究从储能寿命、荷电状态等因素出发，协调优化混合储能内部出力，本质上是为了改善系统经济性，最大化提升资源利用效率。但是，其考虑因素不够全面，忽略了经济性与储能系统安全稳定运行要求的相互制约，而且也未进一步研究控制参数变化对于混合储能系统整体运行性能的影响。

基于以上因素，本文在之前成果的基础上[11-12]，进一步提出基于混合储能分层优化模型的控制参数优化方法。首先介绍了本文所采用的基于双层模糊控制的混合储能控制策略，并利用在此基础上构建的混合储能优化模型，综合考虑经济性、储能寿命、平抑效果及调整裕度，对小波包分解参数进行再优化。算例结果表明本文提出的方法不仅能实现对小波包分解参数的量化分析，还可以从多方面提高混合储能控制效率，保障其安全可靠运行。

1 混合储能控制策略

1.1 基于小波包分解的功率初次分配

由于风力资源波动性和不确定性高，使得风电机组出力不确定性大，而小波包分解由于其良好的时频局部化特性和多分辨率分辨能力[13]，可以依据风电出力频段分布特点将其分解为低频并网功率Plow、次高频分量Pbat以及高频分量Psc，其分解结果如下：

式中，N为小波包分解层数；nc为次高频与高频的频段划分节点；P(N,x)与P(N,y)分别为风电功率经小波包分解后的第N层的x、y 节点分量；此外，次高频分量Pbat以及高频分量Psc分别由电池和超级电容承担。

上式中，小波包分解层数N决定了对波动分量分解的细微程度，其值越大，风电并网曲线越平滑，但是相对应的储能承担分量越大，储能配置要求越高，经济性越差；其值也不宜过小，否则难以满足相应的并网要求。而频段划分节点nc则直接决定了电池和超级电容间容量功率的分配。nc如果过大，电池承担的能量过高，会加大电池容量需求，而且高频分量的增加使得充电次数增大也会损耗电池寿命；nc如果过小，由于超级电容能量密度低，会使得其荷电状态频繁越限甚至出现容量不足的问题。此外，小波包分解层数N与频段划分节点nc之间还存在相互制约的关系，层数N变化，每一节点上的波动分量大小也会变化，应存在某一最优的节点nc使得混合储能综合性能最优。

因此，本文将基于优化模型对小波包分解参数进行优化，寻找最优控制参数，定量分析其对于混合储能配置的影响。

1.2 双层模糊控制策略

风电功率经过小波包分解后，实现了混合储能内部功率的初步分配以及风电并网功率的获取。为了进一步优化储能出力，协调解决混合储能系统运行过程中可能存在的荷电状态越限现象以及容量功率不足等问题，本文采用基于超前控制的双层模糊控制策略[12]，其基本流程如图1所示。

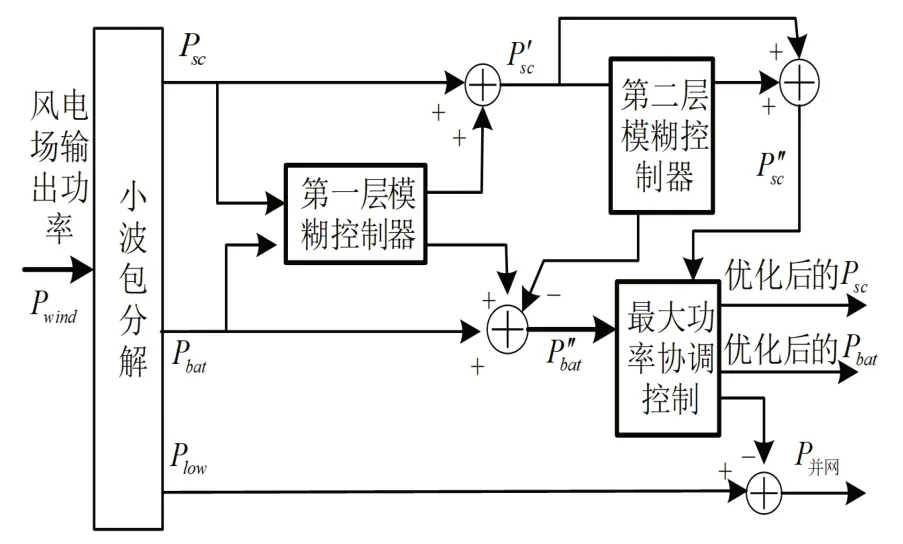
图1 控制策略示意图

从图中可知，风电功率经过小波包分解后，将初步分配好的电池功率Pbat以及超级电容功率Psc送入第一层模糊控制器，第一层模糊控制器通过对电池未来1 h 的出力进行预测，综合考虑电池在预测周期内的越限电量及荷电状态值，调整混合储能内部出力分配。而第二层模糊控制通过加大超级电容在低值荷电状态时的充电功率或高值荷电状态时的放电功率，以保证在不过多增加电池充放电次数的前提下迅速调整超级电容荷电状态值。此外，为了解决在某些极端情况下，混合储能调节能力不足问题，通过最大功率协调控制模块，在考虑储能容量和功率限制的条件下，由另一储能设备承担部分或全部越限功率。通过上述控制模块后的功率分配如公式(2)所示：

式中，k1.x(t)与k2.x(t)分别为两层模糊控制器输出的控制参数；β为功率协调因子，取β=0.3；Pe.bat与Pe.sc分别代表电池和超级电容的额定充放电功率。

2 混合储能控制参数协调优化方法

2.1 优化目标

鉴于现有方法多是依据风电功率出力频段分布和储能特性确定小波包分解参数，参数选取往往无法实现系统性能最优，本文提出通过构建优化模型，并利用寻优算法对小波包分解参数进行优化。本文采用的优化模型[11]综合考虑了经济性、储能寿命、平抑效果及调整裕度等因素，具体优化目标如下：

式中，Sinv、Srep、Sope、Spro、Sunb分别代表初始投资成本、替换更新成本[14]、运行成本、维护成本和不平衡功率惩罚成本；Pgrid为风电平抑后的实际并网功率；NL与NL′为控制前后的寿命损耗系数；Norm(x)为归一化函数；α代表寿命改善因子，取α=0.4；Δt为采样时间间隔，本文Δt=0.5 s;Msc(i)为单位时间段内的超级电容裕度，通过计算Δt内超级电容荷电状态曲线与上下限间面积得到。

上述目标函数中，f1是混合储能经济性评估函数，由初始投资成本、替换更新成本、运行成本、维护成本和不平衡功率惩罚成本组成，描述了混合储能系统的全寿命周期成本；f2是波动平抑目标函数，描述了混合储能系统的波动平抑效果；f3是储能控制效率优化函数，描述了控制过程对电池寿命的影响以及优化后电池的健康程度；f4是超级电容的容量裕度函数，描述了超级电容的备用容量裕度大小。

为了便于算法寻优求解，采用加权求和的方法将多目标函数转化为单目标函数，如式(4)所示：

式中，ωi为目标函数权重，通过层次分析法计算结果为[0.677 4,0.181 8,0.093 4,0.047 4]。

2.2 优化流程

上述优化模型综合考虑多方面因素，可从整体上提升混合储能系统的运行性能和可靠性。本文基于该模型，采用改进遗传算法进行寻优，为了减少计算量，首先基于平抑效果和平滑度判断，对寻优参数范围进行缩小，其过程如下：

2.2.1 参数寻优范围

依据现有标准[15]，对不同分解层数下的有功功率波动值进行计算，可知N=8 层时，1 min 与10 min 波动值分别为1.820 MW 和6.708 MW，考虑到数据存在的波动性，保留一定裕度，可认为9 层以上小波包分解可满足平抑需求。再对各层并网曲线进行对比分析，如图2 所示。按照平滑度来说，12 层已经较为理想，分解更多层数，储能容量配置成本将急剧增加，不利于经济性的提升，因此本文确定小波包分解参数优化范围为9-12层。

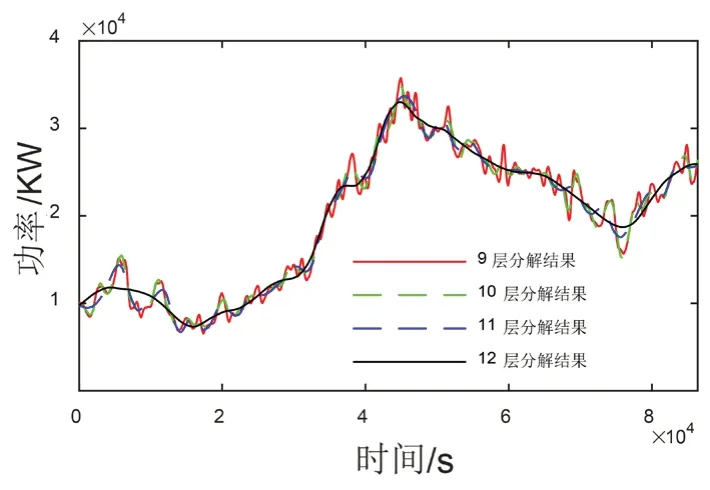
图2 风电期望并网功率随分解层数变化图

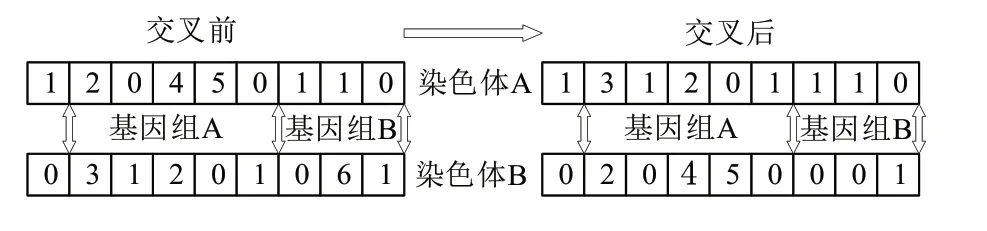
图3 交叉操作示意图

而对于频段划分节点nc来说，考虑超级电容响应速度，其一般用于平抑0.007 Hz 以上的波动，可采用式（5）确定nc上限值。

式中，fs为采样频率，fs=1/Δt。

最终，nc的取值范围为[1,nx]。

2.2.2 基于基因组的改进遗传算法

基于以上理论，本文采用基于基因组的改进遗传算法进行寻优，其优化模型求解过程如下：

1）将储能的小波包分解参数及容量功率作为优化变量，按照1.2.1 确定取值范围后，生成初始种群。

2）对初始种群进行解码，获取小波包分解后的风电并网功率期望值及混合储能功率初步分配值。

3）将种群中个体送入双层模糊控制器，基于风电典型日出力数据进行控制，获取混合储能实际出力结果。

4）将混合储能出力数据输入优化模型中，获取各目标函数值，并将转化后的单目标函数值F 作为个体适应度。

5）基于基因组的概念，对于不同类型数据，如小波包控制参数、容量功率配置参数分别单独进行选择、交叉、变异，以防止出现不可行解，其中选择交叉概率分别取为0.9 与0.01。

6）判断此时是否达到收敛条件或迭代次数k是否达到最大迭代次数（Ngen=100），满足条件则迭代结束，否则返回步骤2）对种群进入下一次迭代。

7）输出结果，获取参数优化结果。

整体优化流程如图4所示：

图4 参数优化流程图

3 算例分析

本文算例采用某装机容量为48 MW 的风电场典型日出力数据，算例中电池的允许充放电深度为20%～80%，初始荷电状态为0.5，超级电容的允许充放电深度为25%～95%，初始荷电状态为0.5，充放电效率均为0.95%。最终优化结果见表1 及表2。

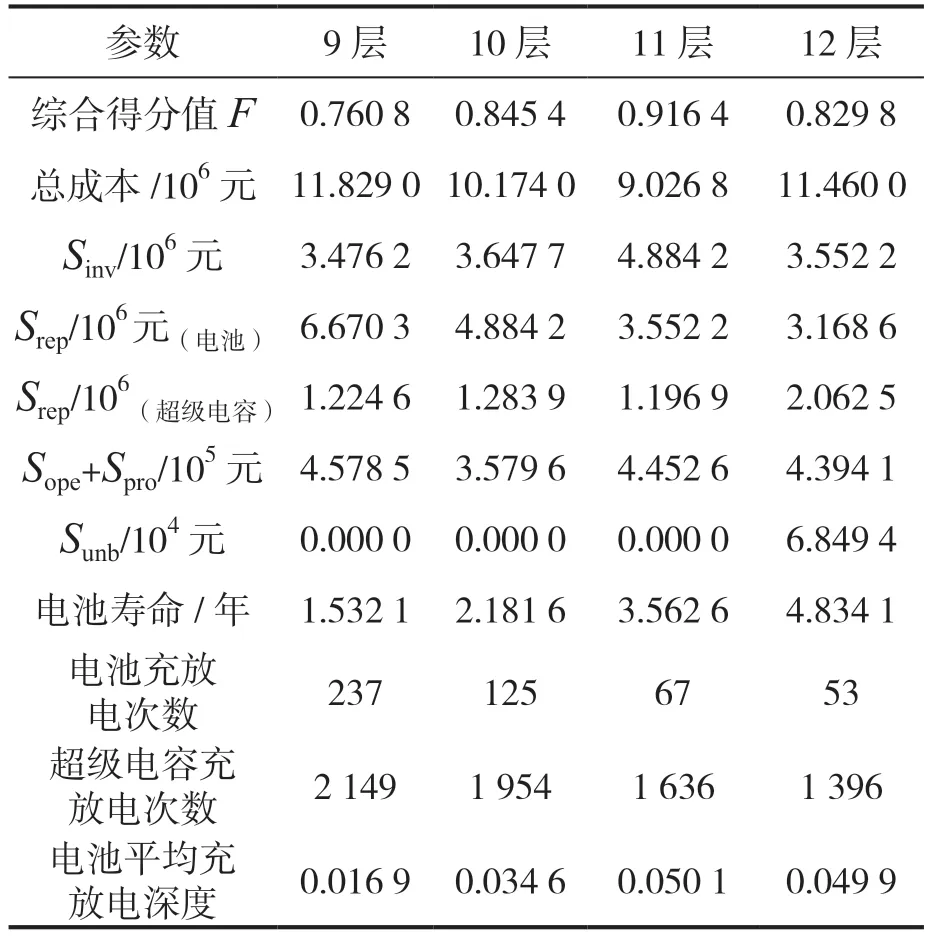
表2 混合储能相关指标计算结果

从表1 可以看到在9-12 层范围内，节点nc最优值均为1，这是因为混合储能更新替换成本占总成本比重达到30%～60%，保持较低的nc值则分配给电池的波动分量的波动频率和能量越低，使得电池的充放电次数以及充放电深度都可以得到控制，如图5 所示，随着N的增加，电池更新替换成本在不断降低。

图5 电池寿命与充放电次数随N 变化情况

而从表2 与图6 可以发现，混合储能系统的总成本并未随着层数N的增加单调上升，分析其原因，在11 层以前，随着N值的增加，如前述分析可知，电池更新替换成本在不断降低，总成本因而也不断降低。但是在N＞11 层后，由于分配给超级电容的能量值过高，使得超级电容需要更大的容量以完成平抑要求，如表1 可知，N=12 层时的超级电容容量配置大小是11 层时的2.17 倍，因此总成本反而升高。由图6 也可知，N=11 层时混合储能系统配置方案综合得分最高，此时其综合性能最优。

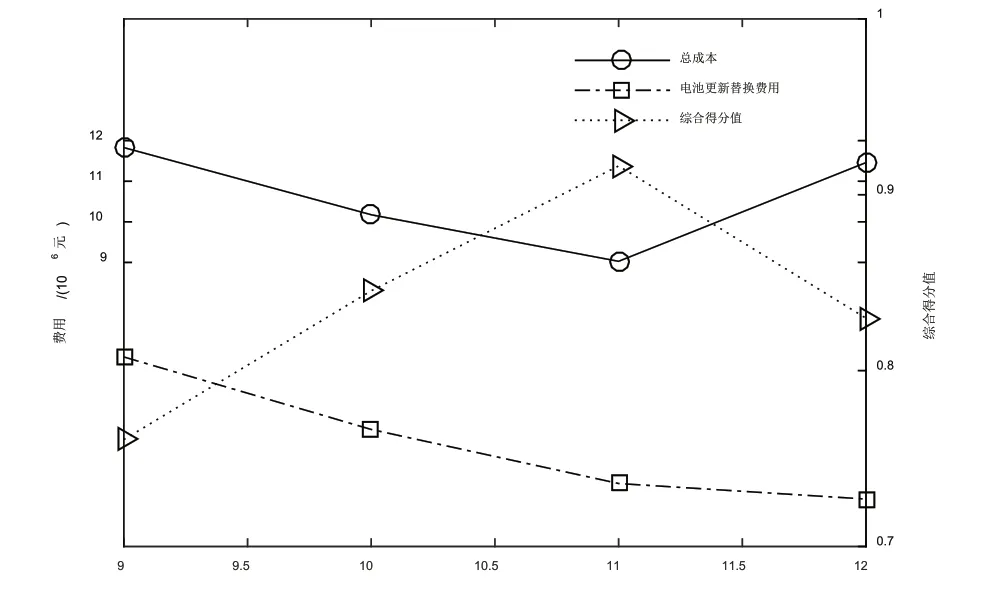
图6 优化模型参数随N 变化情况

因此，从以上分析中可以发现，由于经济性因素、储能寿命、储能运行性能、平抑要求等多方面因素的影响，小波包分解参数N与nc都会对混合储能综合运行性能产生影响，存在某一最优分解层数和判断划分节点，可以实现混合储能系统总成本最低，使得其整体运行性能最优。

4 结论

针对小波包参数优化问题，本文提出基于混合储能优化模型的控制参数优化方法，其结果表明：小波包分解参数的确定不能仅仅依赖于风电数据频段分布特点和储能特性等因素，混合储能系统的经济性和运行性能间的相互制约也会对控制参数的确定产生重要影响，需要建立一个科学合理的评价模型进行定量分析。本文通过算例分析验证了该优化方法在对小波包分解参数定量分析中的有效性，确定了最优分解的N与nc，通过该方法可以确定出最优的分解层数与频段划分节点使得混合储能系统经济性和整体运行性能最优，保证电力系统安全稳定可靠运行。