基于改进粒子群算法的百色水库发电优化

杨 帆，卢学良,黄荣泽

（1.广西右江水利开发有限责任公司，广西 南宁 530000；2.百色新铝电力有限公司调度中心，广西 百色 533000）

0 引言

科学有效地制定水库的中长期发电优化调度，可以在保证水库各项安全约束的条件下提高水资源利用率，增加水库的运营收益。水库的中长期发电优化调度是一个多变量、多维度、多约束的典型非线性优化问题，实际优化过程中会遇到“维数灾”问题。对此，许多学者对水库发电优化问题进行长期研究，提出了许多高效的算法，对水库发电优化调度起到极大的推动作用[1-4]。动态规划法能够高效解决非线性、多维数等优化问题而在水库发电优化领域得到推广，文献[5]利用全域搜索法生成优化问题的初始解，然后通过不断的迭代在局部空间内逐步靠近最优值，以达到降维的目的，有效降低高维度优化模型对算法效率的不利影响；文献[6]利用组合遍历和多层嵌套两种方法降低模型维度，大大提高计算效率。近年来，智能算法由于其概念简单、对优化模型维数不敏感、可以获得全局最优解等优点，在水库发电优化领域得到广泛应用。其中，粒子群算法（Particle Swarm Optimization，PSO）在水库发电优化领域应用较多，文献[7]将人工免疫算法与PSO 结合求解水库发电优化模型，提高了算法适应性；文献[8]将模拟退火与PSO结合求解水库发电优化模型，提高了PSO 的全局搜索能力。基于已有的研究，为提高百色水库的发电经济效益，本文建立百色水库年发电优化模型，并采用改进的粒子群算法(improved particle swarm optimization，IPSO)对模型进行求解，最后以百色水库数据为例进行仿真以验证所建立模型和算法的有效性。

文章内容安排如下：首先建立百色水库年发电优化模型，然后介绍用于求解发电优化模型的改进的粒子群算法（IPSO），最后以百色水库往年的月平均来水数据为基础对模型进行验证分析。

1 水库发电优化模型

1.1 目标函数

本模型以一个调度周期内百色水库的发电量最大为目标函数：

式中，E为一个优化周期内水库的总发电量，本文以一年为优化周期；n一个优化周期内总的时段数，本文以一个月为一个时段，所以n=12；Δt为一个时段的时长；Ni为一个时段内的发电量，具体表达式如式（2）所示：

其中，η表示水库水电站的发电效率系数；Qi为i时段的发电流量；Hi为i时段水头。

1.2 约束条件

1）水量平衡约束

式中，Vi、Vi+1表示i、i+1 时段水库的水量,Qini、Qt为t时段的入库流量和出库流量。

2）水位约束

Zmin、Zmax分别表示水库水位的上下限。

3）出力约束

Nmin、Nmax分别表示水库水电站发电出力的上下限。

4）出库流量约束

Qmin、Qmax分别表示出库流量上下限。

5）期末水位约束

为保证汛期来临前水库腾出足够的库容，一个优化周期结束时需保证水库水位处于规定的范围，本文规定3 月份为优化周期结束时间，具体表达式如下：

Zindex为调度周期结束时的水位。

2 改进粒子群算法

为提高粒子群算法的寻优速度和效果，对普通粒子群算法做3 个方面的改进，具体在2.1-2.3 小节介绍。

2.1 改进粒子群初始值生成

传统粒子群算法的初始种群由伪随机数生成，因而容易产生较多的劣解，导致算法易于收敛于局部最优解，影响算法的全局搜索能力。为解决算法易陷于局部最优解的束缚，本文采用混沌动力学模型映射生成初始种群[9]，表达式如下：

式中，rand∈(0,1),rand≠0,0.25,0.5,0.75,1。

式中，K∈N,0 ＜ZK+1＜1。

式中，i=1，2，3，....n。

利用混沌动力学模型生成粒子的初始值，首先利用式（8）生成随机数rand 作为混沌系列的初始种子z0，再利用式（9）生成混沌系列的映射值zk，接着根据式（10）得到第i个粒子的初始值xi，式（10）中D为粒子个体的维度。由于混沌系列对初值非常敏感，所以可以避免粒子个体初值过多集中于局部最优解附近。

2.2 粒子群速度、位置的更新

传统粒子群算法速度公式和位置更新公式中的惯性权重和学习因子均为常数，容易造成粒子陷于局部最优解。为增加粒子的全局搜索能力，扩大搜索范围，本文利用蒙塔纳算法生成粒子速度公式中的学习因子[10]。该算法如下表达式如下：

其中：

式中，β为[1,2]之间的参数,Γ为标准伽马函数。

根据式（11）-（12），经改进的位置速度公式如下：

2.3 粒子弹射激活机制

传统粒子群算法在粒子陷入局部最优解后无能为力，因此本节采用混沌动力学模型对粒子重新初始化的方式，重新将使粒子置于空间上的不确定位置，该方法类似于把陷于局部最优解的粒子从该位置弹射出去[10]，其逻辑具体表达式为：

式中，Fitbest表示粒子当前处于的最优解；Chaos函数表示利用混沌动力学原理将粒子的位置重新初始化，具体表达式见文献[10]，这里不再赘述。

2.4 基于改进粒子群算法的水库发电优化调度流程

根据上文对粒子群算法的改进，总结出基于改进粒子群算法的水库发电优化调度流程如下：

1）利用混沌动力学原理初始化粒子个体的初始位置和速度；

2）计算各个粒子的适应度，并记录其历史最优解；

3）根据自适应学习策略，更新粒子的惯性系数和学习因子；

4）根据蒙塔纳算法更新粒子的位置和速度，并更新个体历史最优解；

5）判断粒子是否陷于局部最优解，若有则利用混沌弹射机制重置粒子位置后，粒子返回步骤（2）重新计算；

6）判断约束条件是否满足，若满足则输出计算结果，否则返回步骤（2）。

3 实例验证及分析

3.1 百色水库概况

以百色水库为例，水库的安全约束条件有：水库正常蓄水位228 m，相应库容48 亿m³；最高洪水位233.45 m，相应总库容56 亿m³；防洪限制水位214 m，防洪库容16.4 亿m³；死水位203 m，死库容21.8 亿m³；水库调节库容26.2亿m³，属不完全多年调节水库。水库水力发电厂装机容量540 MW。以水库2021 年的月平均来水为数据基础（表1 所示），验证所提模型和算法的有效性。

表1 百色水库2021 年月平均入库流量 m³/s

3.2 优化调度结果

设置发电优化调度模型的初始水位为195 m，按照1 个月为一个时段，1 年为一个调度周期，利用MATLAB 编程计算，优化结果如下：

从图1 可以看出，虽然两种算法最终都能够找到已知的最优解，相比较于PSO，IPSO 获得的初始值更优并且更快地收敛于最优值，陷于局部最优解的次数明显减少，表明IPSO 跳出局部最优解的能力更强，全局搜索能力得到提高，拥有更强的鲁棒性和实用性。

图1 IPSO 与PSO 算法寻优曲线对照图

3.3 改进粒子群初始值效果分析

为了分析IPSO 优化效果更佳的原因，图2画出PSO 和IPSO 的初始水位值，从图中可以看出，PSO 初始水位值集中在196 m ～202 m 之间，而IPSO 初始水位集中在196 m ～215 m 之间，表明采用2.1 节的改进粒子群初始值生成方法后，初始值范围更大，有利于算法跳出局部最优解和提高收敛速度。

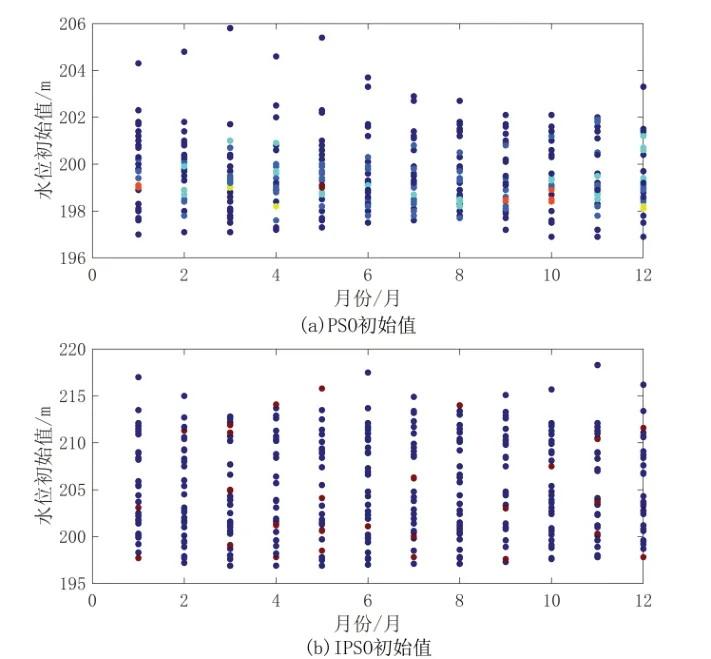
图2 不同算法初始水位分布图

3.4 粒子位置、速度更新及弹活机制改进对优化结果影响分析

为分析改进粒子位置、速度更新及弹活机制对优化结果的影响，通过对PSO 和IPSO 两种算法迭代过程分析，得到PSO 最终的收敛值为第9 号粒子，IPSO 最终的收敛值为第27 号粒子。图3 为PSO 第9 号粒子和IPSO 第27 号粒子收敛时的水位曲线，从图中可以看出，在丰水期（6月、7 月、8 月、9 月）IPSO 优化过程中比PSO维持更高水位，表明经过改进粒子位置、速度更新及弹活机制后增加粒子的全局搜索能力，扩大搜索范围，保证最终收敛值收敛于全局最优解。

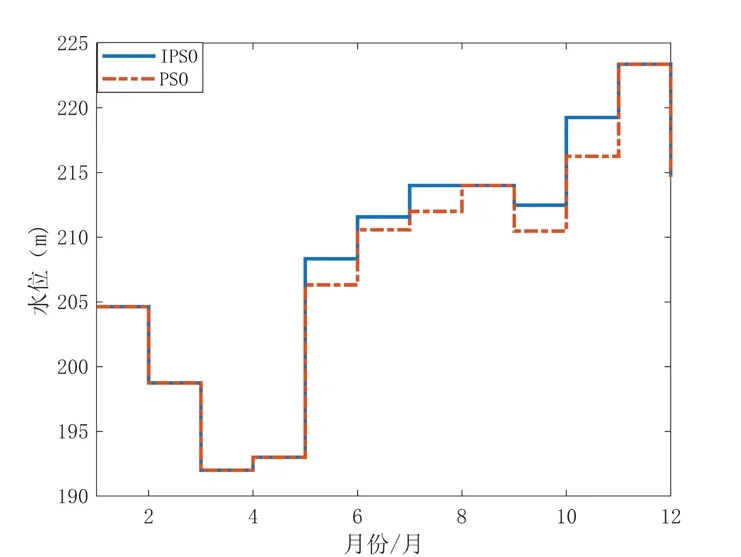
图3 收敛时各月份水位曲线

3.5 算法改进前后月发电出力和弃水量对比

算法改进前后月发电出力和弃水量如图4所示，从图中的优化结果可以看出：

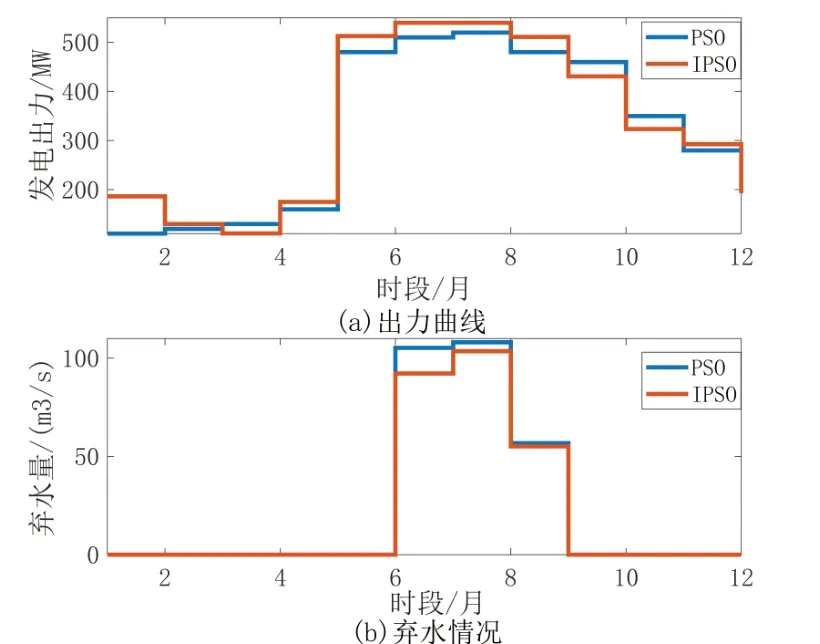
图4 月发电量和弃水量对比

1）优化后在一个发电周期内水库保持较高的水位运行，保证水库发电机在同样的发电出力情况下消耗的水资源更少。汛期来临前，水库尽可能发电提前将库容腾空，汛期保持水位在警戒水位水平，多余水量只能通过弃水来保证水库安全。汛期结束后则尽可能地蓄水，保证冬季的水库发电能力。

2）在丰水期（6 月、7 月、8 月、9 月）水库无论优化前还是优化后均保持在警戒水位运行，发电量大，同时弃水也较多，虽然控制水库水位在警戒水位以下运行时，会导致洪水发生时大量弃水，但可以保证水库安全。

3）汛期过后，水库利用台风带来的降雨等有利条件增加蓄水量，充分发挥了水库蓄水能力，为电网迎峰度冬提供了重要电量储备。

4 结论

本文建立百色水库年发电优化模型，模型充分考虑水库的来水特性、汛期安全运行约束等因素，并以改进粒子群算法为模型解法，利用往年水库的来水数据对模型进行验证，得到以下结论：

1）改进粒子群算法初始值产生方法后，水位初始值范围更大，有利于算法扩大搜索范围，跳出局部最优解和提高收敛速度。

2）改进粒子位置、速度更新及弹活机制后，算法可以使水位陷于局部最优解后跳出，增加粒子的全局搜索能力。

利用水库年发电优化模型，可以根据年初来水的预测结果，制定水库的年发电计划，实现在汛期来临前腾出库容拦截洪水，汛末拦尾蓄水的功能，充分发挥水库的防洪功能，提高水库发电效益。由于百色水库所在流域的来水预测不可避免存在偏差，今后的工作是进一步分析研究水库流域降雨成因及误差分布规律，提高来水预测的准确性，为水库的调度决策提供更多的科学依据。