输电线路跨越式巡检机器人越障运动优化

吴 毅，吴功平，黄 乐

（武汉大学动力与机械学院，湖北 武汉 430072）

1 引言

输电线路作为输送电能的重要途径，其稳定可靠性关系到国计民生，定期对其巡检尤为必要。巡检机器人作为代替人工巡检的重要手段，通过搭载成像设备，沿输电线路运动，对线路金具进行巡检巡视，已成为各科研院所的研究热点［1］。机器人越障是巡检过程中的重要技术难题，其中，时间与能耗是影响越障的关键因素［2］。

越障运动要求机器人具有低时耗与低能耗的特点。文献［3］采用双臂交替越障方式，运动规划较为复杂，且并未对越障运动进行优化。文献［4］将机器人三个驱动关节的均方根功率消耗之和作为目标函数，利用Taguchi方法优化关节偏移量，通过比较原始模型和优化模型发现RMS功耗减少了25%以上。文献［5］基于机器人动力学构建了永磁交流伺服电动机驱动的点焊作业机器人轨迹能耗模型，采用蜜蜂进化型遗传算法求解最优能耗轨迹。文献［6］采用三次和五次多项式拟合关节轨迹，利用加权系数法围绕时间与能耗构建以绿色度最大为目标的优化模型，对纤板生产机器人运动参数进行了优化，并对比两种关节轨迹的优化结果。现有研究对运动优化问题的处理，主要是基于机器人动力学构建面向时间与能耗的优化目标函数，通过对机器人运动参数的优化，得到更低时耗或能耗的运动轨迹。

针对输电线路巡检机器人的跨越越障运动过程，采用五次多项式对关节空间运动轨迹进行插值以避免加速度冲击带来的振动，以无碰避障运动条件和运动学参数作为约束，构建基于动力学的面向时间与能耗的越障优化模型，利用弹性系数法消除时间和能耗在数量级上的差异所产生的影响。为避免算法陷入局部最优，平衡算法的全局与局部搜索能力，对传统粒子群算法引入记忆项惯性权重的自适应调整机制。通过仿真分析与无碰避障运动条件验证模型的有效性。

2 巡检机器人及越障规划

2.1 机器人系统

输电线路跨越式巡检机器人由奇臂、偶臂、导轨、机箱组成，采用双臂反对称式布置［7］，如图1所示。奇臂和偶臂包含多个运动关节，通过关节动作的排列组合运动完成越障。机器人沿着输电线路运动，通过搭载网络云台摄像机对金具进行监视拍摄，完成巡检任务。

图1 巡检机器人模型及坐标系Fig.1 Inspection Robot Model and Coordinate System

机器人的关节动作包括：行走轮用于使机器人沿输电线路运动；夹爪关节用于夹持导线，确保机器人越障时不偏离导线；伸缩关节用于机器人的提升和下降，实现机械臂的离线和落线；俯仰关节用于实现竖直平面内的俯仰运动；旋转关节用于实现水平平面内的旋转运动；错臂关节用于实现机械臂之间的交错运动。机器人通过上述6 个关节的排列组合运动，完成对不同障碍物的越障。

2.2 越障运动规划

输电线路由杆塔、地线、导线、金具等组成，架空地线悬挂于杆塔之间，线路上分布着防振锤、悬垂线夹、耐张线夹等金具。机器人沿着架空地线运行时，金具会成为阻挡其顺利通过的障碍，通过对不同的障碍物采取相应的动作策略，才能完成机器人越障运动。

当通过小坡度防振锤群时，机器人采用双臂伸长直接滚动方式越障，越障成功与否取决于对行走轮的控制。该越障方式运行效率高，时间短，所需能耗较少，但由于受防振锤群数量以及间距不确定等因素的影响，难以判断越障进程，导致越障可靠性降低。

当通过大坡度防振锤群、悬垂线夹时，机器人采用跨越越障方式，两个机械臂交替离线、落线进行越障。如图2 所示，机器人先进行前进碰检定位障碍物，然后单臂离线，通过错臂运动跨越过障碍物，执行落线动作，另一机械臂重复以上动作即可完成跨越越障。该方式可靠性高，但耗时长、所需能耗大，运动优化针对此方式。

图2 跨越越障动作序列Fig.2 Obstacle Crossing Action Sequence

3 越障运动优化模型

3.1 目标函数建立

机器人在关节空间的运动轨迹是由若干路径点组成的，可用多项式来对路径点进行插值。常用的插值函数包括三次和五次多项式，三次多项式以位置和速度参数作为运动学约束，计算方便，但因未考虑加速度变化而可能造成关节运动的冲击，导致机器人损坏，五次多项式在三次的基础上引入了加速度约束，使关节运动更平滑。设机器人第i(1 ≤i≤n)个关节在第m(1 ≤m≤l)段运动轨迹中，途径起始路径点的时刻为tims，途径终止路径点的时刻为time，第m段轨迹的广义位移、广义速度、广义加速度分别为可以得到第i关节第m段运动轨迹的五次插值函数为：

其中，起始和终止路径点需满足如下运动学约束条件：

联立求解式（1）、式（2）可以得到五次多项系数：

机器人在关节空间的动力学广义力矩可由Lagrange方程导出，Lagrange方程定义如下：

式中：L—Lagrange函数；K—系统动能；P—系统势能。

于是可以求得机器人的动力学方程为：

机器人运动学参数及动力学方程推导过程见文献［8］，忽略各关节之间的摩擦力，可以得到关节i所需的广义力矩为：

式中：Dij—关节之间的惯量项系数；Dijk—向心力项和哥氏力项系数；Di—重力项系数。

已知机器人各个关节在第m段轨迹的起始和终止时刻分别为tims和time，各关节在每一段轨迹的运动是同步的，可以得到越障运动总时间为：

通过前面求得的关节运动轨迹及广义力矩，可以得到机器人越障运动的总能耗为：

以运动时间短，能量消耗少作为优化目标，可以得到机器人越障运动优化目标函数：

式中：η1、η2—时间和能耗的权重系数，满足η1+η2=1；α—弹性系数，用以平衡时间和能耗在数量级上的差别所产生的影响。需要满足的运动学和动力学约束条件为：

3.2 无碰避障运动条件

在机器人跨越越障错臂运动阶段，如图3所示。障碍物可以抽象成包络其的矩形区域，机器人需转开一定角度使离线行走轮避开此矩形区域，并确保错臂运动过程中不与障碍物区域发生干涉，完成错臂运动后再转回至导线处。

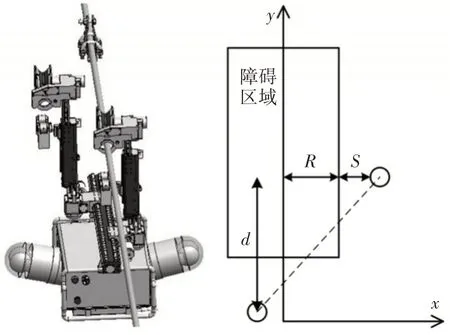
图3 无碰避障示意图Fig.3 Schematic Diagram of No Collision Avoidance

在该模型中，设机器人离线行走轮与障碍物区域的距离为S，则有如下表达式：

式中：d—错臂运动距离；θ—旋转关节运动角度；θ0—行走轮偏置形成的固有角度；R—障碍物区域一半的距离。只有当S在越障过程中始终大于零，机器人才能完成无碰避障运动。

4 越障运动优化算法

4.1 自适应粒子群算法

粒子群优化算法作为一种进化计算方法，通过模拟鸟群的捕食行为，实现群体中个体之间的信息共享与运动协作来寻求最优解。与其他智能算法相比，粒子群算法工程实现易，参数调节少，对非线性问题具有较好的收敛性［9］。

式中：c1、c2—学习因子，取c1=c2=2；r1、r2—（0～1）之间的随机数；w—记忆项惯性权重，权重大便于全局搜索，权重小便于局部搜索。

定值权重往往不能兼顾全局搜索和局部搜索，通过引入对记忆项惯性权重的自适应动态调整机制，可以平衡全局搜索能力和局部搜索能力，其核心是权重随着粒子适应度值的变化而动态调整［10］，规则如下式：

式中：f—当前适应度值；favg—平均适应度值；fmin—最小适应度值。

同时，引入惩罚函数将约束问题转化为无约束问题，定义辅助函数如下：

式中：Fun(x)—目标函数；gi(x)≥0(1 ≤i≤λ)—第i个不等式约束；σ—惩罚因子，取初始值σ0=1，在优化过程中按σk+1=μσk递推更新。

4.2 算法描述

针对巡检机器人的越障运动优化问题，对传统粒子群算法引入了自适应惯性权重调整机制，该算法的流程描述，如图4所示。

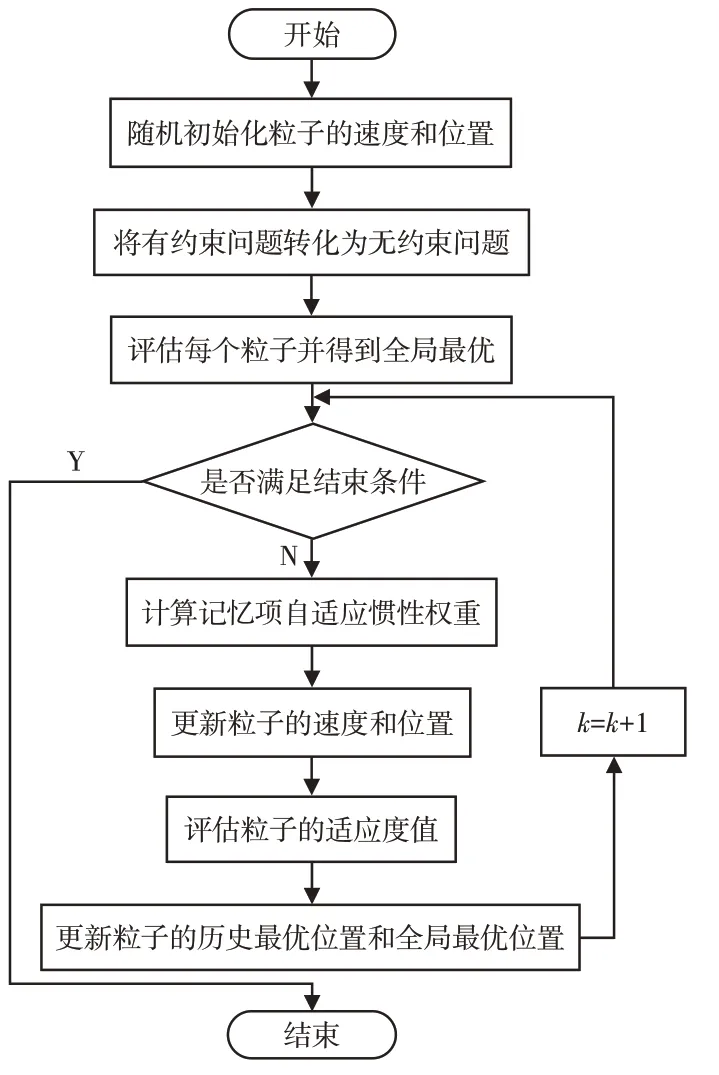
图4 算法流程图Fig.4 Algorithm Flowchart

算法步骤如下：

（1）随机初始化粒子的速度和位置，利用惩罚函数将有约束问题转化为无约束问题。

（2）评估每个粒子的适应度值并得到全局最优，判断是否满足结束条件。

（3）根据适应度值计算记忆项自适应惯性权重，通过在解空间中搜索，动态更新粒子的速度和位置，评估粒子新的适应度值。

（4）搜寻并更新每个粒子的历史最优位置及群体的全局最优位置，其中，全局最优位置作为当前最优解，迭代次数增加一次。

（5）判断是否满足结束条件，如不满足，则返回步骤（3），通过反复迭代寻优，如满足，则输出适应度值及全局最优位置作为优化结果。

5 仿真结果与分析

针对输电线路巡检机器人的跨越越障运动过程，前文已给出越障运动规划，由于双臂越障过程相似，以其中一个臂越障为研究对象，将机器人在运动过程中所需要经过的关键路径点转化成关节空间中的角度，将这些路径点用前文所述轨迹连接起来即可形成越障轨迹。各关节的具体运动参数，如表1所示。其中，关节2、关节3、关节5、关节6为旋转关节，关节1、关节4、关节7为平移关节。

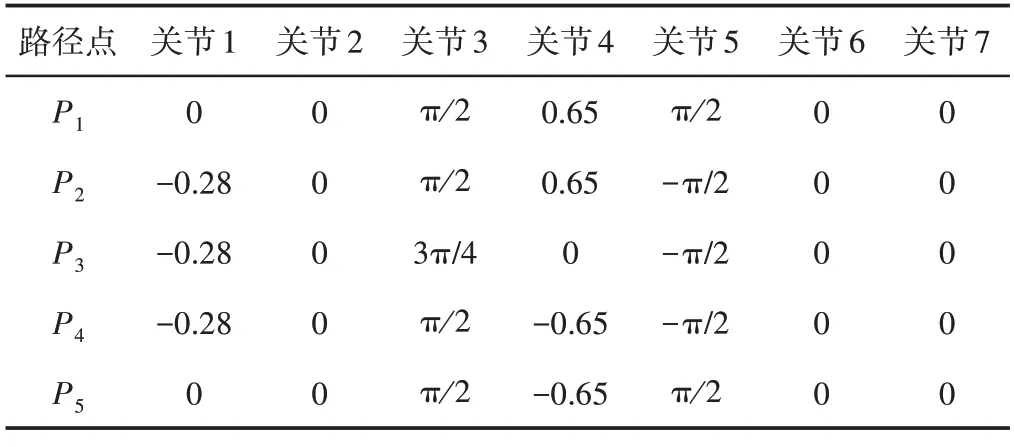
表1 机器人越障运动关节参数Tab.1 Robotic Obstacle Crossing Motion Joint Parameters

设置每一段轨迹的初始时间间隔分别为10s，7s，7s，10s，在MATLAB中运行改进的粒子群算法，实验参数设置为：种群规模n=50，最大迭代次数K=200，惯性权重w的变化范围为（0.4～0.9），时间和能耗同等重要，故取权重系数η1=0.5，η2=0.5，弹性系数α=0.05，求得的四段轨迹运动时间分别为13.36s，6.24s，6.05s，13.67s，具体优化结果，如表2所示。由表可知，优化后的越障时间增加了15.6%，越障能耗减少了17.9%，总的适应度值减少了3.8%。优化结果表明，在该模型下，机器人的越障时间与越障能耗得到了有效平衡。越障运动各关节的位置、速度、加速度变化曲线（零值曲线未标出），如图5所示。由图可知各关节运动光滑且连续，采用五次多项式插值的轨迹拥有较好的加速度性能，没有加速度冲击，满足越障平稳性要求。

表2 算法优化结果Tab.2 Algorithm Optimization Results

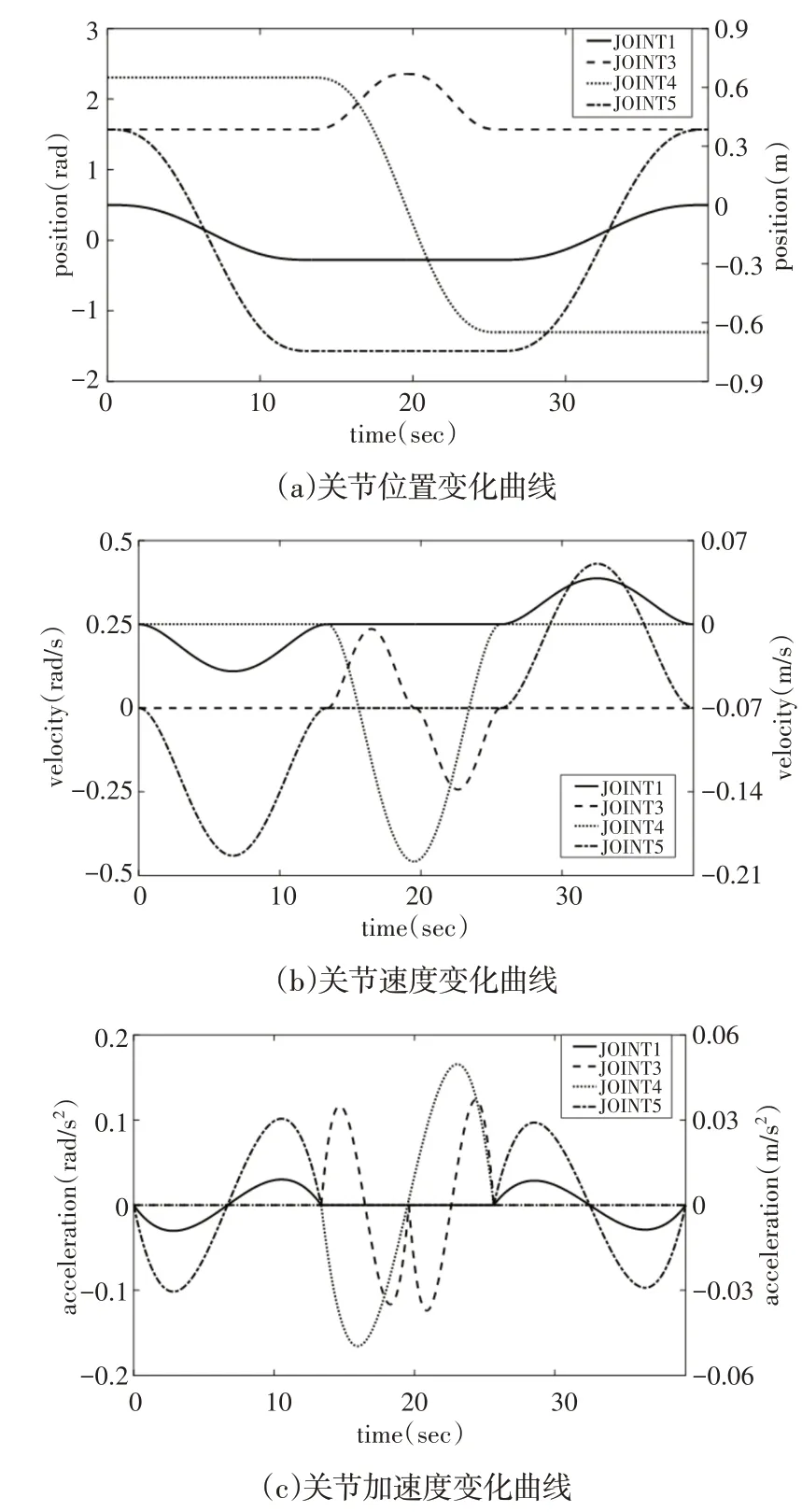
图5 各关节位置、速度、加速度变化曲线Fig.5 Change Curve of Joint Position，Speed，Acceleration

针对机器人的避障要求，已知θ0=8°，R=0.05m，错臂阶段行走轮与障碍物区域之间的距离变化曲线，如图6 所示。距离在（0.04～0.36）m之间变化，机器人在越障过程中不会与障碍物区域发生干涉，满足无碰避障运动条件。

图6 行走轮与障碍物距离变化曲线Fig.6 Change Curve of Distance between Walking Wheel and Obstacle

6 结论

针对输电线路巡检机器人的跨越越障运动过程，基于运动学参数采用五次多项式对关节空间路径点进行插值生成运动轨迹，在推导动力学方程的基础上建立了面向时间与能耗的越障优化模型，同时指出了机器人的无碰避障运动条件。利用改进后的自适应粒子群算法对越障模型进行优化，仿真结果表明，在该模型下，机器人的越障时间与越障能耗得到了有效平衡，关节位置、速度、加速度曲线平滑，满足越障平稳性要求，离线行走轮与障碍物区域之间的距离满足无碰避障运动条件。为进一步研究其他障碍物环境下的越障运动提供重要依据。