四模块可变形机器人转向性能评价体系构建

王相鑫，李延斌，常 健，王 聪

（1.沈阳工业大学机械工程学院，辽宁 沈阳 110870；2.中国科学院沈阳自动化研究所机器人学国家重点实验室，辽宁 沈阳 110016；3.中科院机器人与智能制造创新研究院，辽宁 沈阳 110000）

1 引言

可变形机器人越来越多的被应用于灾后救援类型的工作中，面对各种灾害过后具备不同特点的所形成的非结构化环境，可变形机器人因其具备多种构型所形成的多种运动模式可以适应具备不同地形特点的非结构化环境，正因这种特点使得可变形机器人在灾后救援方面具备独特的优势［1-3］。

可变形机器人的工作环境决定机器人的行走机构设计相当重要。而在轮式、足式和履带式这三种行走机构中，履带式行走机构具备结构简单控制容易的优点，在具备优点同时也有着转向性能差，运动过程中出现滑移现象等缺点。文献［4-5］都对履带式机器人的转向滑移现象进行深入的研究并提出一定的解决办法。履带式行走机构转向性能差的原因并不是只是因为滑移现象的存在，还存在着很多其他的影响因素，例如，地面摩擦系数，履带材料，机器人构型等因素，这些因素都会对最终的转向性能好坏产生影响［6］。因此要形成相对完善的转向性能评价体系需要在对转向性能进行研究的同时，完善转向性能的误差分析，形成准确的、系统的分析过程。通过确定性能评价指标来完成对四模块可变形机器人的转向性能的理论研究。对于四模块可变形机器人来说，转向性能需要检测两种影响因素，分别是转向灵活性以及转向半径。对于机器人在转向过程中其他对转向运动有影响的因素，可以将其归类为误差因素中，计算相应的影响系数即可进一步完善对四模块可变形机器人的转向性能分析从而最终完成四模块可变形机器人的转向性能评价体系构建［7］。

这里主指在于研究四模块可变形机器人的转向性能研究，可以使得四模块可变形机器人在灾后环境中能够用适宜的构型进行转向运动。主要需要解决四模块可变形机器人的转向性能评定问题，制定一个规范的，合理的性能评价体系，能够更加快速准确的确定各构型所具备的转向性能高低。

2 机器人结构说明

这里主要的评价对象是四模块可变形机器人，外形，如图1所示。

图1 四模块可变形机器人Fig.1 Four Module Deformable Robot

四模块可变形机器人主体是由四个相同的履带式模块机器人组成，通过模块间的连接臂连接同时也通过连接臂作为变形的媒介。模块左右两侧各有一个俯仰关节和偏转关节用来进行构型变换。该机器人主要优点在于构型可变且构型数量较多，众多的构型令机器人具备强大的环境适应能力，共拥有22种构型，不同的构型具备不同的特点。具体构型变化［8］，如图2所示。

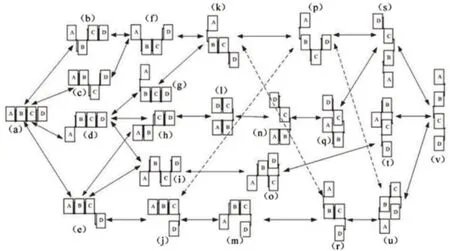
图2 四模块可变形机器人构型变化Fig.2 Configuration Change of Four Module Deformable Robot

四模块可变形机器人众多构型中不同的构型拥有不同的运动性能适应性，当四模块可变形机器人进行转向运动时，可以分为两种模式，分别适应不同的机器人构型。一种为大半径转向运动模式，主要是通过内侧模块与外侧模块形成速度差进而形成转向力矩达成转向的目的，在运动空间足够的前提下，适合大部分构型。另一种模式为小半径转向，主要是通过内侧模块与外侧模块通过方向相反的运动方向，达成在较小的空间内进行转向的目的，这种运动模式适用于部分对称构型。在小半径转向运动模式中除了传统小半径转向外，还有协同小半径转向运动模式，这种运动模式基本运动原理与小半径转向运动类似，但在此基础上，通过多模块共同运动将部分转向阻力变为动力，帮助机器人进行更快的转向。该模式不仅能够在较小的空间内进行转向运动，而且因为其独特的运动原理，使得原本无法进行小半径转向的构型能够进行小半径转向运动这种转向模式进一步扩大了小半径转向的适用范围。

3 大半径转向运动分析与性能评价

针对四模块可变形机器人的大半径转向进行运动学分析，来确定转向运动性能评价指标。在进行构型选择时，选择的构型，如图3所示。因其较为平衡的各项运动性能指标以及在进行构型描述的时候比较全面。结合四模块可变形机器人结构特点与运动学相关知识做出如下分析：

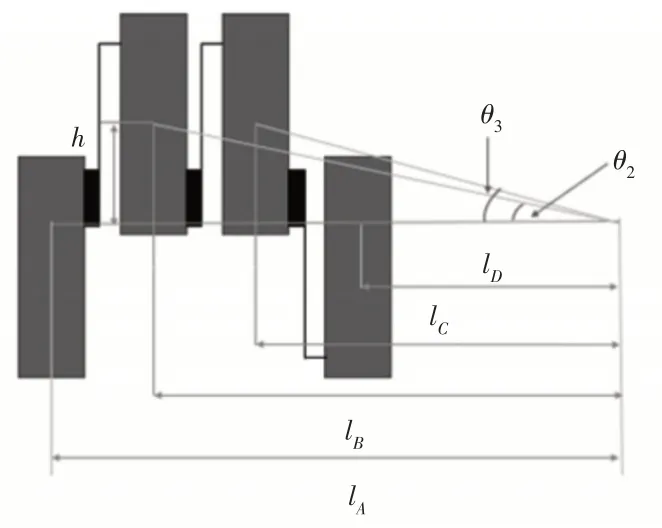
图3 大半径转向参数说明Fig.3 Description of Large Radius Steering Parameters

当四模块可变形机器人做出大半径转向运动时，基本符合基本运动原理，原理如式（1）所示：

结合当前机器人结构特点与式（1）得到结果如式（2）所示

式中：l—转向中心与模块重心的水平距离；d—转向中心与模块重心距离；θ—各模块重心与转向中心连线与转向中心与机器人整体重心连线夹角；v—模块运动速度，具体说明，如图3所示。

针对大半径转向运动，通过对运动原理的研究与分析，了解四模块可变形机器人在进行大半径转向运动时更加注重当前环境的可运动距离，然后才能判定当前环境是否能够进行当前构型的大半径转向运动，因此确定转向半径为大半径转向运动的性能评价指标，式（2）中可以确定转向半径。转向半径大小定义为：靠近转向中心一侧模块中心与转向中心的横向距离，即：

式（2）中可知当速度确定时，就可以求出转向半径大小，即转向半径与四模块可变形机器人各模块运动速度有关系。机器人驱动轮由驱动电机直接驱动，由此可以得到如下公式：

式中：n—驱动电机输出转速；i—驱动电机到驱动轮的减速传递比；v—模块运动速度。

结合式（2）、式（3）可得到转向半径，如式（6）～式（8）所示：

式中：a—相邻模块重心的距离；

h—模块重心到转向中心的垂直距离。

通过式（6）可知，可以对机器人转向运动产生影响的分别为当前机器人所处的构型和当前模块运动速度。通过式（6）～式（8）三式可知当前构型对大半径转向运动的影响程度。

4 小半径转向运动分析与性能评价

四模块可变形机器人的小半径转向运动因为机器人的运动特点可以分为传统小半径转向运动以及协同小半径转向运动。其中协同小半径转向运动主要通过抬升部分阻碍转向运动的模块的方式来减小模块产生的阻力矩，从而达到加快转向运动的目的。因此此次分析主要针对传统小半径转向运动。根据四模块可变形机器人结构建立简化小半径转向模型，如图4所示。

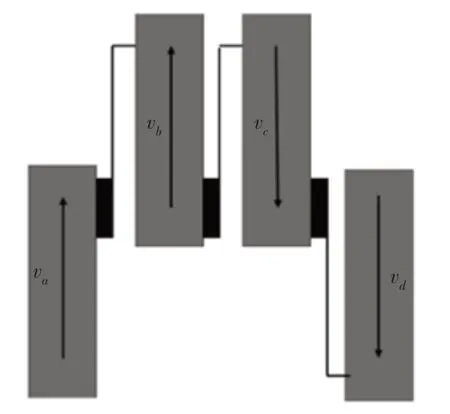
图4 小半径转向运动模型Fig.4 Small Radius Turning Motion Model

通过图4所建立简化模型结合转向运动基本要求建立如下运动学分析：

通过当前构型确认当前理想状态的转向速度比与转向中心的关系式，如式（9）所示。通过简化之后的构型结合小半径转向运动原理，四模块可变形机器人会处于向左转向的运动状态，对当前机器人运动姿态进行动力学分析：

式中：b1—模块宽；b2—模块间隙；Fa—各模块牵引力；fa—地面阻力矩。

式（10）中Fa通过机器人结构特点与运动原理可计算结果为式（11）所示。

式中：η1—传动系统传递效率；η2—履带运动磨损系数，其大小为η2=0.95-0.0017v［10］；T—电机输出扭矩；i—齿轮系传动比；rk—驱动轮半径。

在结构设计时令控制台重量与模块重量相同，结合图5可以得出转向阻力矩为：

图5 小半径转向运动转向力矩Fig.5 Steering Torque of Small Radius Steering

式中：μx—垂直方向地面摩擦系数；m0—模块重量；l—模块长度；r—履带轮半径。

根据重力平衡条件结合图5所示的当前构型可得重心偏移位置：

式中：Δm—控制台重量；

l—模块长度。

结合式（13）与式（12）可以进一步变为：

式（10）～式（16）中可以详细的对四模块可变形机器人在进行转向运动时所受力的大小与方向，对机器人转向运动的运动原理进行了完整的说明，最终可得四模块可变形机器人在进行小半径转向运动时的力矩和为：

式中：TT—四个模块机器人的转向力矩。

四模块可变形机器人在进行小半径转向运动时因转向半径较小，因此对于转向半径这一评价指标不进行计算，但是因为需要机器人进行近似的原地转向，使得机器人在转动相同角度时相比大半径转向运动需要克服更多的转向运动产生的阻力，因此需要定义另一种评价指标：转向灵活性［9］。通过转向灵活性来确定机器人转向的困难程度，计算方式为直线运动时电机输出功率与转向时机器人运动输出功率的比值。同时也以此为评价标准对机器人的多种构型进行小半径转向性能评价。

小半径转向的评价指标转向灵活度β主要用来计算相同情况下转向运动与直线运动相比输出功率产生的变化，变化越小则转向越灵活。具体计算公式如下：

当四模块可变形机器人处于直行状态时四个模块处于同速前行状态，因此输出功率相同即：

式中：Pd—模块输出功率；

PS—四模块可变形机器人处于直线运动时的输出功率。

当四模块可变形机器人处于转向运动状态时输出功率为：

由式（18）～式（20）可得：

结合式（7）、式（14）可以得到转向灵活性为：

由于小半径转向运动转向中心一般与当前构型几何中心相近，因此结合式（22）可以得出针对四模块可变形机器人在进行小半径转向运动的通用转向性能评价指标，如式（23）所示。

式（21）中可以看出对小半径转向运动的性能评价指标可以产生影响的有两种，其中一种是当前构型，另一种是电机转速。

5 仿真平台搭建与实验验证

5.1 大半径转向运动仿真分析

通过对大半径转向运动的运动学分析，建立速度与转向半径的数学模型，并通过Matlab软件对该模型进行分析，并将分析过程分为两种类型：

第一种主要针对相同构型条件下，不同速度对转向半径的影响程度。并设定初始参数，如表1所示

表1 初始参数Tab.1 Initial Parameters

通过初始参与的设定与数学模型的建立，所得结果，如图6所示。

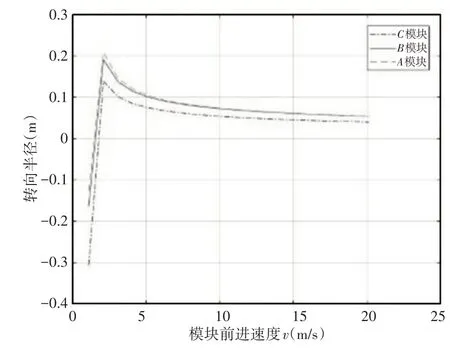
图6 速度转向半径数学模型Fig.6 Mathematical Model of Speed Turning Radius

该类型分析主要针对相同构型条件下不同模块的速度变化对转向半径会产生的影响程度大小。通过图7可以看出转向半径随着速度的增加而增加但在增加到峰值后会开始产生回落，并最终降低到稳定值。同时距离D模块越远对相同速度变化条件下转向半径变化影响程度越大，同时有效速度越大（有效速度指转向半径大于0的速度值）。

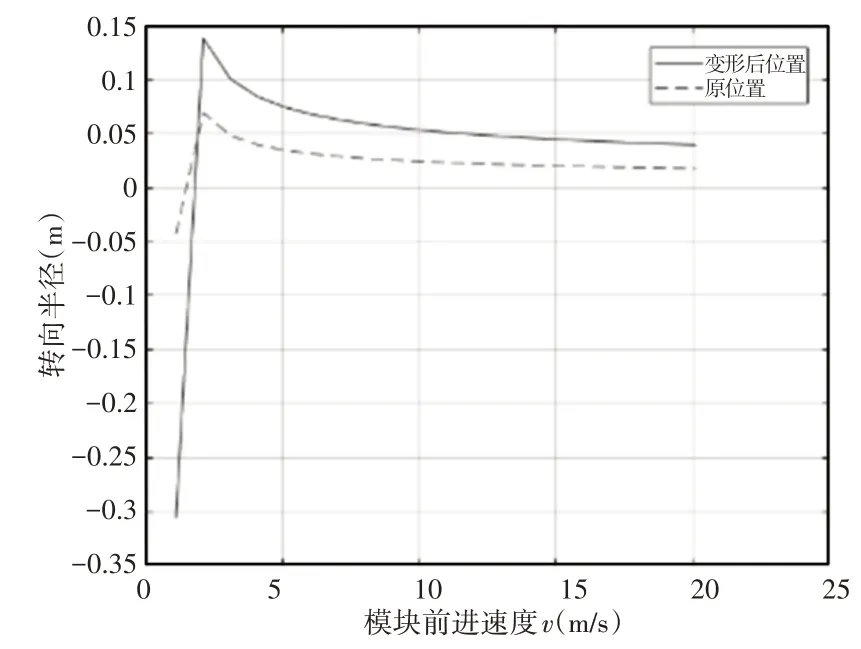
图7 模块位置与转向半径关系Fig.7 Relationship Between Module Position and Steering Radius

第二种，针对同一模块处于不同位置时速度对转向半径的影响结果，如图7所示。

初始设置共有两种位置设定，第一种为仅俯仰模块运动产生的垂直方向位置h变化，第二种为仅偏转模块运动，即水平方向l变化，从图中可以看出当垂直方向位置h产生变化时，即图7所示结果，会使转向半径最大值减小，增大速率减慢，但也更早会带平稳转向半径。当水平距离l发生变化时，即图7中虚线所示结果，可以看出与实线相比更早进入有效运动速度，但转向半径最大值变小。

通过以上分析可以得出以下结论：

（1）针对四模块机器人进行大半径转向运动时在需求控制转向半径时，提供各模块运动速度提供参考区间。

（2）模块运动速度变化会对当前构型运动产生一定的影响，但当超过峰值后会影响程度会逐渐下降。

（3）构型会因为l或者h数值的变化对转向半径产生影响但只会改变相应转向半径对应的速度区间，并不会改变速度变化对转向半径变化的变化趋势。

针对以上结论，使用机器人实物进行验证实验，实验结果基本符合计算结果，试验过程，如图8所示。

图8 大半径转向实验验证Fig.8 Experimental Verification of Large Radius Steering

5.2 小半径转向运动运动性能仿真建模

四模块可变形机器人在进行小半径转向运动时，因为运动特点可知转向半径无法作为评价性能指标，因此引入转向灵活性这一概念来对小半径转向运动进行性能评价。

通过对转向灵活性进行数学建模分析，并使用matlab进行仿真，主要针对模块当前运动速度与所受牵引力两种参数作为主要影响参数，两种参数通过式（5）、式（11）可知分别对应电机输出转速与电机输出扭矩，考虑机器人所选电机特点，选定电机输出电流来对扭矩进行调节，最终得到结果，如图9所示。

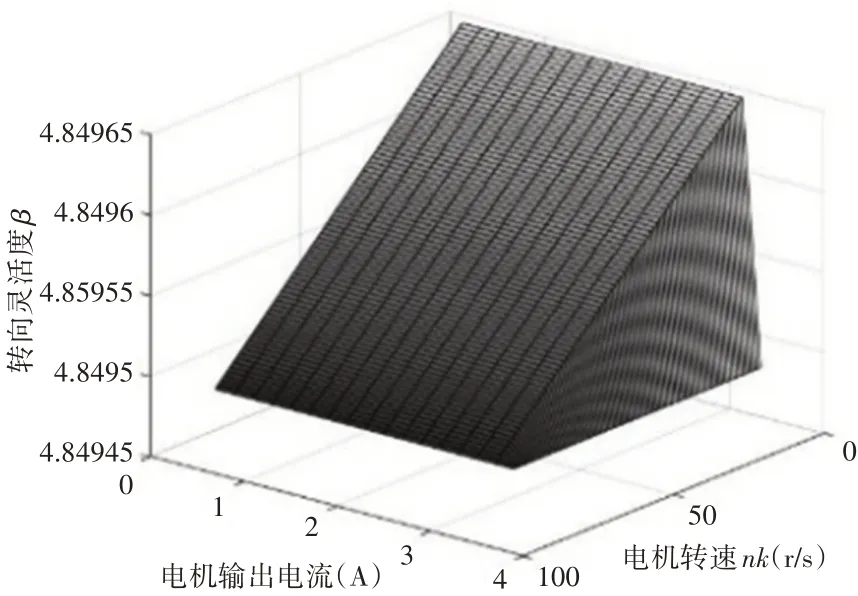
图9 转向灵活度Fig.9 Steering Flexibility

图9中可以看出相比较于电机输出电流电机转速在转向灵活度影响程度上相差不多，但电机转速主要集中于［3，4］这个数值区间对转向灵活度产生影响，而电机输出转速则在整个［0，100］工作区间都会产生影响。

接下来对该图进行详细分析，忽略电机转速对转向灵活性的影响得到的图像，如图10所示。图10中可以看出在电流比较小的情况下对转向灵活度并没有影响，当电流超过2.6的情况下转向灵活度急剧下降，可以说明在转速一定的前提下，电机扭矩变大到一定程度才会加强机器人的转向灵活度，对四模块可变形机器人小半径转向运动产生有益影响。因此在进行小半径转向运动时可以优先选择功率区间较大的参数组合。在一定的电机输出电流的前提下，得到的图像，如图11所示。

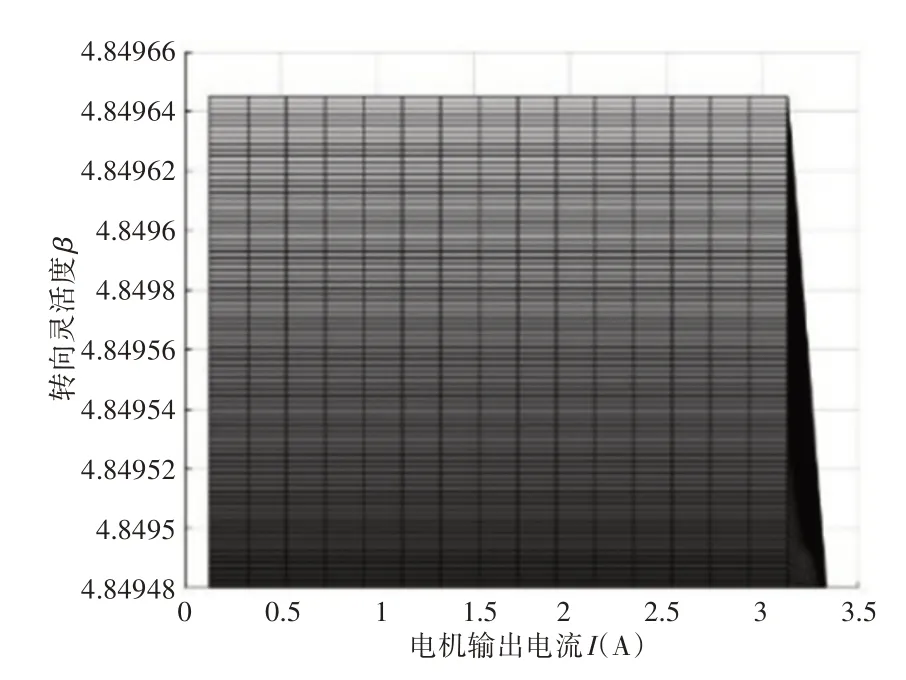
图10 电机电流对转向灵活度的影响Fig.10 Influence of Motor Current on Steering Flexibilit

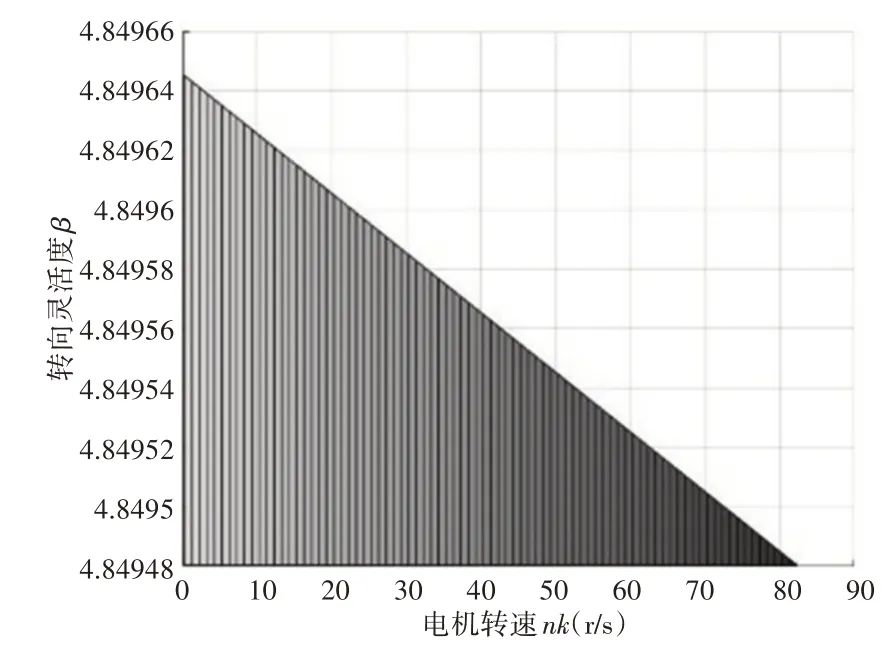
图11 电机转速对转向灵活度影响Fig.11 Influence of Motor Speed on Steering Flexibility

在电机输出电流确定的条件下，转向灵活度与电机转速成一定比例下降的趋势，即在四模块可变形机器人在进行小半径转向运动时电机转速越大对转向运动的增益越强。

通过以上建模分析可以得出结论：四模块可变形机器人进行小半径转向运动时需要对电机动力参数区间进行选择，适宜的动力参数区间会对转向运动有良好的增益效果。

结合以上结论，并通过机器人实物进行实验并得到的结果，如图12所示。通过统计电机输出功率并通过计算得到转向灵活性数值然后与计算结果相互验证，所得结果与计算结果偏差均不超过10%，最终结果基本符合预期计算结果。实验结果，如表2所示。

表2 转向灵活性实验数据Tab.2 Steering Flexibility Experimental Data

图12 小半径转向运动实验Fig.12 Small Radius Turning Motion Experiment

6 结论

（1）通过对四模块可变形机器人的转向性能评价指标进行研究，完成四模块可变形机器人性能评价指标体系的一部分，并且加深对四模块可变形机器人的转向性能的认知程度。通过确定两项转向运动性能指标对机器人的转向运动性能进行评定，通过转向灵活性与转向半径两项指标分别对不同构型的两种转向模式分别进行了鉴别，结合多项运动性能的运动性能指标完成对构型变换网络的优化，剔除部分无法完成的构型与变换途径，简化构型变换途径，加强构型变换网络的目的性。

（2）通过性能评价指标的确定对四模块可变形机器人的转向性能部分从理论模型变为数学模型，进一步加强四模块可变形机器人在实际应用中的狭窄空间运动的能力。通过对构型的转向性能的进一步理解，当机器人处于灾后现场时，可以有目的性的使用对应构型进行应对与解决。