高空作业车观测器与神经网络滑模控制器设计

胡海东，陈浩然

（内蒙古科技大学信息工程学院，内蒙古 包头 014010）

1 引言

随着我国城镇化的迅速推进，高空作业的需求日益增加。折叠臂高空作业车通常是使用汽车作为运载工具，安装在汽车底盘上的系统，其结构，如图1所示。它具有机动性、灵活性等独特优点，由液压缸作为驱动力实现机械臂的举升，从而将人员运送到指定位置进行安装和维护作业，并且在建筑、市政、消防等行业中和工厂生产过程中被广泛应用，对我国的经济建设有重要的意义。由于轻质长臂杆的广泛使用，高空作业车臂架系统的弹性形变不容忽视。弹性形变的存在，会引起工作平台运动过程中的振动现象，因此，要保证工作平台的稳定性，需要使用合适的方法描述高空作业车机械臂的弹性变形，建立符合实际情况的动力学模型，并设计合适的控制方法抑制臂杆弹性形变引起的振动。文献［1］对折臂式高空作业车进行了运动学建模，但并未考虑臂杆的弹性形变。描述弹性形变主要有有限元法［2］与假设模态法［3］等。文献［4］应用有限元法描述臂杆的弹性形变，建立了折叠臂高空作业车的动力学模型，并通过ADAMS软件进行了运动学仿真验证了系统的稳定性。但有限元方法存在计算效率低，计算成本昂贵的缺点。动力学建模主要有拉格朗日方程方法以及牛顿－欧拉方程方法［5］等。文献［6］针对折叠臂高空作业车使用假设模态法描述弹性形变，使用拉格朗日方程方法建立了动力学模型，并通过数值仿真表明臂架的柔性变形明显，柔性变形对臂架的稳定性影响不能忽略不计。基于此模型，对高空作业车工作平台的运动控制问题进行了研究。

图1 折叠臂高空作业车结构图Fig.1 Scheme of Folding Boom Aerial Work Platform

在不增加测量装置的情况下，设计观测器能够有效提升控制性能。针对现实情况下臂杆柔性模态变量难以测量以及存在外界扰动的问题，设计扩张状态观测器能够对外界扰动以及系统的模态变量进行观测，将观测值用于闭环控制能够提升系统的鲁棒性。文献［7］针对柔性臂系统设计了扩张状态观测器对系统状态变量进行观测并对系统不确定项和外界干扰进行估计，通过仿真实验结果验证了观测器能够提升控制性能。

研究人员针对高空作业车及柔性机械臂轨迹跟踪问题提出了多种控制方法，文献［8］针对高空作业车样机设计了PID控制器并进行了实验，但其并未考虑臂杆柔性。文献［9］提出了H∞鲁棒控制器，但只在高空作业车电液俯仰机构单向运行时有较好的性能，双向运行时系统不稳定。文献［10］提出了反步控制器使得工作平台能够较为稳定地跟踪预期轨迹，但该控制方法只能用于精确的系统模型。而滑模控制针对建模不确定性问题具有鲁棒性。

基于上述研究，针对存在柔性模态变量不可测、外部干扰等因素的影响下的折臂式高空作业车轨迹跟踪控制设计了扩张状态观测器与神经网络滑模控制相结合的控制器，该控制器结合了滑模控制的鲁棒性与神经网络的函数逼近能力。文章结构安排如下“，动力学模型”中介绍并分析了折臂式高空作业车的动力学方程；在“观测器的设计与分析”部分中设计了扩张状态观测器，并且通过李雅普诺夫判别定律证明了设计的观测器是稳定的；在“神经网络滑模控制器的设计与分析”部分中设计了神经网络滑模控制器，并且通过李雅普诺夫判别定律证明了设计的扩张状态观测器与神经网络滑模控制相结合的控制器是稳定的；在“系统仿真”部分中进行了高空作业车跟踪控制的仿真研究，仿真实验结果表明轨迹跟踪误差较小且弹性形变变量收敛到较小的值，可证明设计的控制器具有良好的跟踪性能并且柔性臂中存在的振动被有效地削弱“；结语”部分给出了研究内容的总结性结论。

2 基于扩张状态观测器的折臂式高空作业车神经网络滑模控制器设计

针对折臂式高空作业车轨迹跟踪控制问题设计了扩张状态观测器与神经网络滑模控制相结合的控制器，以减小跟踪误差并抑制高空作业车的振动。结合折臂式高空作业车系统、扩张状态观测器、神经网络滑模控制器等部分，得到完整的轨迹跟踪控制框图，如图2所示。图中xd为参考轨迹，滑模控制器计算出控制率τ，使用径向基函数神经网络代替滑模控制中的切换控制对系统不确定项Δf逼近。为模拟现实情况下的扰动问题，在折叠臂高空作业车系统中引入外界扰动d。扩张状态观测器计算出系统状态及外界扰动的估计值。

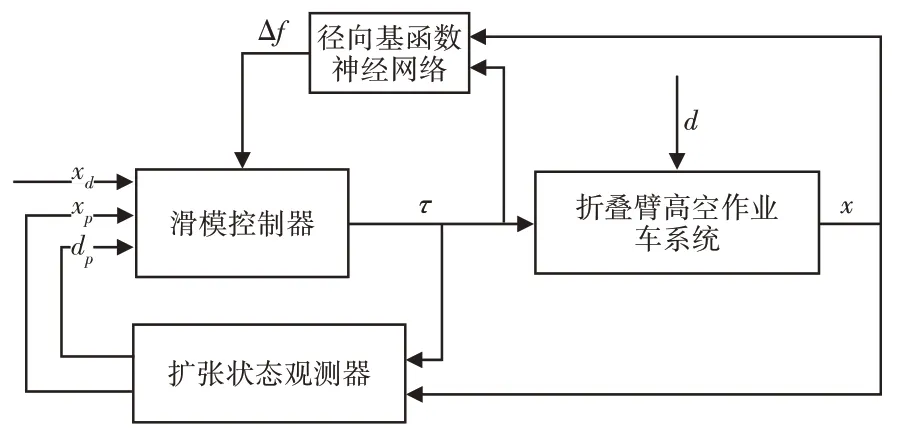
图2 控制结构框图Fig.2 Block Diagram of Control System

2.1 动力学模型

折叠臂高空作业车臂架系统的坐标系，如图3所示。在图1中，选择臂杆1的最底端为坐标原点，沿水平面的方向为x轴，垂直于水平面的方向为y轴，建立惯性坐标系XOY。沿臂杆1的轴线方向为x轴，垂直于其轴线的方向为y轴，建立动坐标系X1O1Y1，同样的方式建立臂杆2的动坐标系X2O2Y2。所建的臂架系统坐标系示意图，如图3所示。

图3 臂架坐标系示意图Fig.3 Schematic Diagram of Arm Coordinate System

根据文献［6］，折臂式高空作业车的柔性多体动力学方程可写为：

式中：

式中：θ1—臂杆1相对水平面的关节偏转角度；θ2—臂杆2相对水平面的关节偏转角度；q11—臂杆1 的一阶弹性形变变量；q12—臂杆1的二阶弹性形变变量；q21—臂杆2的一阶弹性形变变量；q22—臂杆2 的二阶弹性形变变量；l1—臂杆1 的长度；l2—臂杆2的长度；m1—臂杆1的质量；m2—臂杆2的质量；m—工作平台的质量；g—重力加速度；E—臂杆材料的弹性模量；I1—臂杆1横截面的惯性冲量；I1—臂杆2横截面的惯性冲量；A、P、C—质量系数矩阵：

F—q的系数矩阵：

考虑扰动d(t)，且，则系统应为：

将式（3）写为状态方程形式为：

2.2 观测器的设计与分析

针对现实情况下存在臂杆柔性模态变量不可测以及外界扰动的问题，设计了扩张状态观测器用于观测系统的模态变量，并将外界扰动作为系统状态变量进行观测。

将扰动d（t）作为一个系统的增广状态变量，设d（t）的导数为h（t），则可将式（4）改写为：

设计一个辅助系统，以对柔性臂系统状态进行重构：

针对式（6），构造如下观测器：

定义估计误差为：

由式（5）～式（7）可得：

对上述扩张状态观测器进行稳定性分析，取李雅普诺夫函数如下：

整理得：

令w1≥r，v1≥1/2+r，v2≥r-w3。

其中，r=diag[r1r2r3r4r5r6]，ri—正实数。

则：

从而得到：

设R=ρ2/2，r≥ρ/2S，Vo=S

则：

那么当Vo(0) ≤S，t≥0则有Vo(t) ≤S。

解得：

根据以上稳定性分析可知，系统的收敛精度取决于观测器的初始误差以及误差d（t）的上界ρ。并且通过调节r的值使其任意大，可使观测器误差收敛到任意小。

2.3 神经网络滑模控制器的设计与分析

基于滑模控制的鲁棒性与神经网络的函数逼近能力，针对折臂式高空作业车轨迹跟踪控制设计了神经网络与滑模控制相结合的控制器。

定义参考轨迹为xd，将跟踪误差定义为：

选择滑模面为：

式中：c=diag[c1c2c3c4c5c6]；ci—正常数。

定义参考状态：

径向基函数神经网络是一种包括输入层、隐含层、输出层的三层神经网络，径向基函数神经网络的结构，如图4所示。使用了径向基函数神经网络对系统不确定项实时逼近并补偿。

图4 径向基函数神经元网络Fig.4 Radial Basis Function Neural Networks

神经网络输出可表示为Y=OTϕ。

式中：O—神经网络的理想权值矩阵；ϕ—隐含层的输出。

定义系统不确定项为：

式中：O*—径向基函数神经网络的理想权值矩阵；ε—逼近误差。

选择s为神经网络输入。设计神经网络滑模控制率τ为：

根据式（3）、式（15）得：

式中：Ψ—12阶正定矩阵。

令ℵ=[0sT]T，则神经网络权值自适应律设计如下：

式中：Φ=[0ϕT]T—12维列向量；n—正实数。

对李雅普诺夫函数求导并结合上式得到：

根据施瓦茨不等式可得：

上式说明，提出的基于扩张状态观测器的神经网络滑模控制器能够有效抑制工作平台的振颤，保证其跟踪参考轨迹运动。

3 系统仿真

被控对象为式（4），设被控对象参数如下：臂杆1的长度l1为7.5m、质量m1为650kg、抗弯刚度EI1为（6×108）、初始角度θ1为2.09rad、初始角度偏差0rad/s，臂杆2的长度l2为8.5m、质量m2为650kg、抗弯刚度EI2为（5×108）、初始角度θ2为0.52rad、初始角度偏差0rad/s，工作平台质量m为150kg。观测器为式（7），辅助系统中重构状态的偏差系数矩阵分别为：

控制律为式（15），控制律方程中神经网络输入的系数矩阵为：M=50000 diag[1 1 1 1 1 1]

滑模函数中误差的系数为：

定义扰动：

MATLAB仿真结果，如图5～图9所示。

图5 作业车末端位置的跟踪曲线Fig.5 The Trajectory Tracking of the Work Platform

由图5可知，作业车末端工作平台能在短时间内稳定地跟踪参考轨迹，同时抑制了振动。从图6 中可知作业车末端工作平台轨迹跟踪误差较小，可证明设计的控制器具有良好的跟踪性能。图7证明了振动得到了有效抑制。弹性形变变量收敛到较小的值，这意味着柔性臂中存在的振动被有效地削弱。弹性形变变量q11的实际值及其观测值，如图8 所示。由图8 可知观测器能够观测系统不可测状态，且观测效果较好。由图9可知，设计的观测器能够观测扰动d（t）。由图5～图9 可知，所提出的神经网络滑模控制器能够实现高空作业车的轨迹跟踪控制，并且有效地抑制了振动。

图6 作业车末端位置的跟踪误差曲线Fig.6 The Tracking Error of the Work Platform

图7 弹性形变变量q11的变化曲线Fig.7 Curve ofElasticDeformationVariable q11

图8 弹性形变变量q11的观测曲线Fig.8 EstimationandTrackingCurve of Elastic Deformation Variable q11

图9 扰动d（t）的观测曲线Fig.9 Estimation and Tracking Curve of Disturbance d（t）

4 结语

将扩张状态观测器与神经网络滑模控制器相结合研究了折叠臂高空作业车的轨迹跟踪控制问题。扩张状态观测器能够对不可测的弹性形变变量以及外界扰动进行观测，并将观测值用于闭环控制以提升系统的鲁棒性。使用神经网络输出代替滑模控制的切换控制项逼近系统不确定性项，能够削弱切换控制项引起的振颤。

通过李雅普诺夫函数证明了设计的整个控制系统的稳定性和收敛性。仿真结果表明该控制方法能够实现高空作业车工作平台的轨迹跟踪，且末端跟踪误差较小；观测器能够准确地计算出现实情况下系统的不可测状态及外界干扰的估计值；并且使得弹性形变变量快速收敛，有效减小臂杆柔性引起的抖振，从而保证了系统的稳定性与安全性。理论证明与仿真结果均表明该控制方法对于高空作业车轨迹跟踪与振动抑制是有效的。

但目前对折叠臂高空作业车的轨迹跟踪控制问题的研究仅限于仿真研究，后续研究中将通过搭建的实验平台对提出的控制算法进行进一步的验证。