基于卷积神经网络的机械轴承故障智能识别
王 路,殷鸿鑫,刘鸿旭
(1.国能铁路装备有限责任公司肃宁车辆维修分公司,沧州 062350;2.天津哈威克科技有限公司,天津 301799)
作为大型器械运转的基础零件,轴承在制造业的发展与社会生产力水平的提升中发挥着至关重要的作用。然而,多数大型器械运作环境较为复杂,且每日工作量巨大。在连续高强度作业条件下,极易造成轴承零件的磨损失效,导致大型器械损坏并可能引发一系列安全事故[1-2],导致生产中的人员伤亡,造成企业生产的终止,因此部分相关行业研究人员针对故障识别中存在的困难展开了针对性研究。文献[3]在对大型器械运行过程中的轴承振动信号展开采集后,首先利用自适应算法对信号展开多频分割,得到不同频率上的样本信息本征模态分量,从中筛选出能够体现轴承运行状态及故障特征的模态分量,并对其展开特征重构,然后构建深层网络MLCELAE 结构,对重构的轴承振动信号特征展开学习,使MLCELAE 网络具备故障识别功能,并对后续输入信息展开故障判断,此方法在面对多类型的轴承故障识别问题时,故障识别率较低。文献[4]首先利用VMD 方法对轴承振动信号展开处理,以实现轴承振动信号的重构,通过分析重构后的频域信号,实现轴承故障特征信号的提取,然后以多层感知器原理为基础,构建神经网络模型,将轴承故障信号输入到神经网络模型中,结合归一化指标完成PMSM 轴承故障识别模型的建立,进而实现轴承故障的识别,但此方法故障识别效率较低。
以解决上述方法存在的问题作为预期目标,本文提出基于卷积神经网络的机械轴承故障智能识别方法。
1 机械轴承振动信号重构
利用多个传感器实现无损状态下轴承振动信号的采集后,通过小波包分析法对采集信息展开去噪处理。小波包是一组函数,可以用于构建一个包含L2(R)空间的规范正交基库。L2(R)的子空间中,包括正交尺度函数ζ(t)与小波函数ξ(t),设l 为多尺度因子,ζ(t)与ξ(t)的计算公式如下:
式中:iol与iml表示不同的滤波系数。利用二尺度方程内的尺度函数x2n(t)与母小波函数x2n+1(t)对式(1)展开优化,优化结果如下:
当式(2)中n=0 时,则x2n(t)=ζ(t)=x0(t),x2n+1(t)=ξ(t)=x1(t),此时可确定{x2n(t)}为x0(t)=ζ(t)下存在的小波包。
利用小波多变率分析对L2(R)空间进行展开分解,分解后的L2(R)包括{wj}与{xj}2 个子空间。其中{wj}子空间内包含多个尺度函数,{xj}子空间内包含多个小波函数。为实现小波包分解中的二进制变换[5],现令,以此为前提对小波包分解的递推公式展开推导,推导过程如下:
轴承振动信号数学形态表达式为
式中:l=0,1,2,…,2l+1,j=1,2,…,n。基于小波包轴承信息分析原理,对轴承运转过程中的振动信号展开信号重构。根据上述推论,可得到重构无损轴承振动信号的计算公式如下:
通过适当的阈值选择对小波系数展开阈值量化,利用式(4)对原始轴承振动信号展开信号重构,生成高质量的机械轴承振动信号,从而提升信号质量。
2 基于卷积神经网络的故障识别
2.1 基于卷积神经网络的特征提取
卷积神经网络(CNN)是一种前馈网络,能够通过神经网络内部的卷积与池化对输入信息展开拓扑结构逐层分析,利用网络内部算子的运算,实现无损状态下无噪轴承振动信号中特征信号的提取,具体工作原理如图1 所示。

图1 CNN 特征提取过程Fig.1 CNN feature extraction process
机械轴承的振动信号数据通常由大量的数据点构成,在利用CNN 对有效振动信号数据展开特征提取的过程中,由于数据过大,可能导致CNN 网络的超负荷运行,造成特征的模糊提取。因此,所提方法在传统CNN 网络中引入时间步概念[6],利用尺度分割的方式,将输入的大容量轴承振动信号分割成数据点较少的多段数据,并对其展开特征提取。卷积层负责利用卷积核对输入的轴承振动信号展开小范围局部卷积,利用CNN 网络内的激活函数对轴承振动信号实施非线性映射[7]。假设在神经元与特征面的局部连接过程中,表示卷积核在上层特征面中的活动步长,输出特征面的大小ToFM需满足下式要求:
式中:TiFM表示特征面局部输入尺寸;ϑKernel表示当前卷积层内卷积核大小。
设OoFM表示当前卷积层内输出特征面的数量,OiFM表示输入特征面数量,则当前卷积层内的训练参数Oparam的计算过程为
式中:g(·)表示CNN 网络内的线性修正单元的ReLU激活函数,其数学形态表达式为
利用ReLU 激活函数[8]参与卷积层卷积操作的优势在于能够避免过度拟合情况的发生。在卷积层完成了上述一系列卷积操作之后,池化层将以减少网络参数为目的,对卷积层的输出信息展开缩放映射处理,进入下采样操作。池化层通常采用的池化算子包括均值池化算子与最大池化算子2种。均值池化首先对卷积层感知域内的输出平均值展开计算,进而实现轴承振动特征的池化处理,其表达式为
最大池化对卷积层中每个特征面感知域的输出进行处理,在保留最重要信息的情况下将每个感知域的最大值作为输出结果,进而实现对机械轴承振动信号特征提取,结果如下:
式中:ε 表示池化区域宽度。池化层与卷积层对轴承振动信号的多次分析,使输出的轴承振动信号特征具备较好的区分性及鲁棒性,能够较为准确地反映轴承振动信号特征。
2.2 机械轴承故障智能识别实现过程
SVDD 是一种单分类机学习算法,通过将轴承正常运行状态下的特征数据映射到高维特征空间中,进而实现信号分类,从而实现机械轴承故障智能识别。首先将提取到的轴承振动信号特征合集记为Y={y1,y2,y3,…,yj},设映射空间内最小超球面为b,超球面半径为R;为排除轴承振动信号特征样本中的离群点影响,引入惩罚系数D 与松弛因子φj对原始样本中的信息点j 展开处理,以此建立信号分类函数,该函数的描述如下:
式中:Ψ(·)表示非线性函数。为解决函数建立过程中的离散性问题,利用对偶形式对式(11)展开简化内积运算。映射过程中引入核函数L,结合拉格朗日乘子算法[9],利用式(12)实现轴承正常运行状态下,其特征数据在高维空间的特征映射,结果如下:
式中:τ 表示高斯核函数[10]中的宽度参数;βj表示拉格朗日乘子。设y 表示超球面支持向量,若此时拉格朗日乘子满足0<βj<D 条件,则利用式(13)对待测样本z 到超球体中心的距离E 展开计算:
对比轴承正常运转状态下的标准超球距离R,与输入待测轴承信号样本z 到超球体中心的距离E。若E≤R,则判定该信号样本为正常信号,轴承运转状态正常;若R<E,则判定机械轴承故障。
通过以上迭代更新,能够保证轴承机械故障识别的稳定性,避免机械轴承故障智能识别过程中欠拟合与过拟合情况的发生,提高故障识别效率与智能性。
3 实验与分析
为验证所提方法对机械轴承故障识别的准确性,在器械标准运行负载和转速下,选取某一滚动机械轴承作为实验对象,分别利用所提方法、文献[3]方法、文献[4]方法,对轴承故障展开识别。滚动机械轴承实验装置如图2 所示。

图2 滚动机械轴承实验装置Fig.2 Experimental device for rolling mechanical bearings
实验台左侧是两马力的电机(1 hp=746 W),位于中间的是一个转矩传感器,在试验台下方布置一个功率计和电子控制设备,实验测试的轴承支撑着电机轴旋转,一个加速度传感器垂直置于电机输出轴上方外壳上,从而对于实验中的加速度进行测量。滚动机械轴承规格参数如表1 所示。

表1 滚动机械轴承规格参数Tab.1 Specification parameters of rolling machinery bearings
将不同方法的故障信号识别结果绘制成时域波形图像并展开对比,对比结果如图3 所示。

图3 故障识别结果对比Fig.3 Comparison of fault identification results
分析图3 可知,所提方法对轴承故障分析的时域波形与标准波形最相似,证明所提方法对故障的分析更准确。
为验证所提方法的有效性,选取内圈故障、外圈故障、滚动体故障3 种故障类型的机械轴承作为实验样本,分别采用3 种方法对不同故障类型运行状态下的机械设备展开故障识别,识别结果如表2所示。
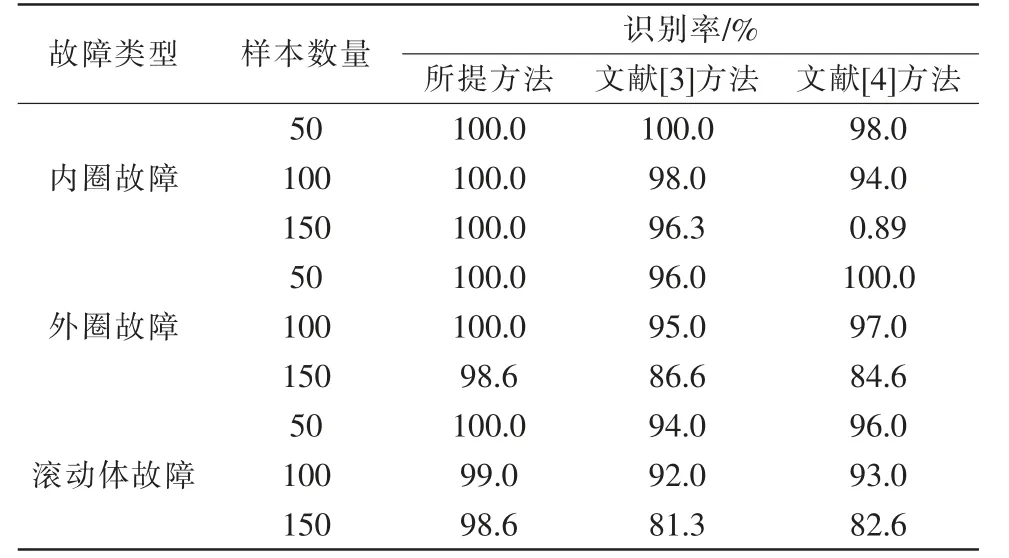
表2 三种类型故障识别结果Tab.2 Three types of fault identification results
观察表2 可发现,所提方法在检测样本数量不断增加的前提下,对内圈故障、外圈故障、滚动体故障3 种类型的故障识别率皆高于文献[3]方法、文献[4]方法。
为验证所提方法的可行性,选取内圈故障轴承、外圈故障轴承、滚动体故障轴承、无损机械轴承样本各100 个,按照故障类型,将样本分为编号为0、1、2、3 四个训练集。引入混淆矩阵对所提方法、文献[3]方法、文献[4]方法的故障类型判别精度展开分析及对比。具体对比结果如图4 所示。

图4 收敛情况对比Fig.4 Convergence comparison
观察图4 可发现,所提方法对不同类型的轴承故障能够做到准确划分,而文献[3]方法及文献[4]方法在多类型轴承故障分类过程中均存在错误划分情况,故障识别效果更好。
4 结语
机械轴承是大型器械运行的核心零件,为保障工业设备的安全运行,需要对机械轴承的损坏及故障展开实时监测。所提方法首先利用小波包分析法,对设备运行过程中采集的轴承振动信号展开去噪处理,利用CNN 网络对振动信号展开卷积、池化,提取振动信号特征,根据振动信号特征提取结果建立基于SVDD 的信号分类函数,该函数通过比较标准超球距离以及待测样本和超球体中心之间的差距实现信号分类,从而实现轴承故障智能识别。

