大型水轮发电机组机械振动信号随机噪声控制

潘 峰，陈建梅，张 伟，龚思宇

（1.中国长江电力股份有限公司，上海 200124；2.北京清能互联科技有限公司，成都 610000）

各国政府为了应对能源结构的变化，纷纷发展新型能源技术。在新型能源中，水力发电作为发电领域中的一种重要形式[1]。此外，水力发电还能在短时间内生产出电网所需的负荷，同时还具备调峰、调频、黑启动等多种优势。然而，大型水轮发电机组的运行状态对于其是否安全运行至关重要。据相关资料表明，通过振动信号数据可以判断出大型水轮发电机组85%的故障状态。然而，由于振动信号容易受到外界干扰的影响，因此在提取过程中易出现误差，从而影响机组状态分析结果[2-3]。因此，需要采用一些去噪方法对振动信号进行控制，以精准地获取机组振动信号，实时监测机组运行状态，延长机组使用寿命。

近年来，学者们对振动信号随机噪声控制方法进行了广泛研究。其中，文献[4]通过谱形变分模态分解和奇异值分解控制随机噪声，得到实际振动信号，精度较高。但是该方法需要进行多次分解和重构，计算量大，且容易出现数据丢失和频率混叠等问题；文献[5]则利用GH Bladed 软件搭建机组模型，将机械振动信号转换成频域信号并通过分析找出噪声信号进行控制，操作简便但需要专业软件和知识；文献[6]则基于变分模态分解和固有模态函数将机械振动信号分解，使用能量熵增量和离散小波包变换控制各层中噪声，并将其余信号融合，速度和精度均较高，但需要进行多次分解和重构，计算量较大。

为解决上述方法中存在的问题，设计一种高效率的大型水轮发电机组机械振动信号随机噪声控制方法。

1 振动信号随机噪声控制方法

1.1 振动信号分层

1.1.1 构建振动信号模态分解寻优函数

变分模态分解法是一种基于交替方向乘子法（ADMM）的寻优方法，其目的是不断更新模态函数及其中心频率，以寻找符合条件的最佳解，进而得出最佳的振动信号分解结果。通过将全局最优问题转换成局部子问题，交替方向乘子法可以高效地找出模态函数。此外，通过拉格朗日函数，可以对中心频率进行最佳解的求解[7-8]。

采用交替方向乘子法搜寻最优解过程如公式（1）所示：

式中：F 表示寻优目标函数；x∈Rn、z∈Rm分别表示优化变量，Rn、Rm表示2 个不同拉格朗日乘子向量集；f（x）、g（z）表示2 个优化问题的目标函数；A∈RP×n描述列数为P 行数为n 的常数矩阵；B∈RP×m描述列数为P 行数为m 的常数矩阵；c=Ax+Bz 为p 个需要优化问题的约束条件不等式。

采用拉格朗日函数对x、z、c 求解，即：

式中：T 为矩阵转换因子；ρ 为平方正则项系数。

通过式（2）可交替算出目标函数x、z、c 的最佳解。

1.1.2 振动信号的模态划分

设定S（t）表示大型水轮发电机组机械含有随机噪声的振动信号，借助傅里叶将S（t）转至频域中，把各频段数据分解成K 个模态分量sk（t），如式（3）所示。采用希尔伯特变换各分量，得出单边频谱如公式（4）所示：

式中：φk、Ak表示第k 个模态分量信号的瞬时频率与幅值；t 即为振动信号采集时间；j 表示虚数单位；δ（t）表示希尔伯特变换函数。

借助指数校正方式将每个模态函数频谱移到各中心频率，再利用式（2）求解此信号梯度平方与各模态函数的带宽，从而得到变分约束问题公式，即：

式中：∂即偏置项；e 表示频谱位移量；w 表示中心频率。

设定｛s｝=｛s1，s2，…，sk｝与｛w｝=｛w1，w2，…，wk｝即为各模态集合与中心频率集。通过上述过程将约束性变分问题转换为非约束性变分问题，求解时需要引入二次惩罚因子α 与y 拉格朗日算子，得出：

式中：n 描述迭代次数；ε 描述随机噪声容限因子。已知判断精度，直到符合式（8）的约束条件，终止更新，即可得到含随机噪声的大型水轮机组机械振动信号分量γ 的取值范围：

1.1.3 变分模态分解层数的确定

在对含有随机噪声的大型水轮发电机组机械振动信号分解之前，需设定振动信号分解层的数量，设定不合理会出现信号数据丢失、频率混叠等问题[9-10]。针对这些问题，采用能量差方式进行求解，计算过程为

式中：E 描述各模态分量振动信号的能量值；u（i）与N 分别描述信号序列与长度。振动信号各分解层能量值均不同，每层能量与初始振动信号能量的差参数求解过程为

式中：Ei1描述振动信号的第i1个模态层的能量；E1描述初始振动信号的能量。

根据ζ 值确定振动信号模态分解层数，在振动信号过分前，k 随着分解层数增加会小幅度增加，而在过分后，则k 会大幅度增加。由此可得出振动信号的分解层数。分解层数从2 开始算出各层的ζ 值，直到k 与极限分解层相等时，分析每一层ζ 值，选取ζ 出现明显增加上一个所对应的k，此k 即为振动信号最终模态分解层数。

1.2 实现振动信号降噪控制

为了掌握大型水轮发电机组机械的实际运行状态，需要控制振动信号各模态层中的随机噪声。通过小波变换，可以得到各模态层的小波系数。对变换后的小波系数进行预处理，即保留系数值较大，控制系数值较小的部分，从而得到大型水轮发电机组机械的实际振动信号。具体过程如下：

式中：i2表示R 的任意元素，寻找R 中最小值rmin，确定rmin对应的k1值，将k1对应的值带入式（12），结果即为恰当阈值：

步骤2将含有随机噪声的各分解模态振动信号sk（t）进行小波变换，得出一系列的小波分解系数；

步骤3将求得的小波系数与Q 对比，大于Q值小波系数保留，此部分即为实际振动信号；反之，即为随机噪声。

通过以上步骤即可完成大型水轮发电机组机械振动信号随机噪声控制。

2 实验

2.1 实验环境

大型水轮发电机组机械振动信号主要由机组机械转频及其倍频构成，且每个频率间幅值均不同。实验选用机组机械由2 Hz 转频于0.5、1.0、2.6 倍频组成。信号数据采集频率为400 次/s，共采集4000个数据，将其作为原始振动信号。如图1（a）所示。为了检测所提方法振动信号随机噪声控制效果，引入随机噪声，如图1（b）所示。

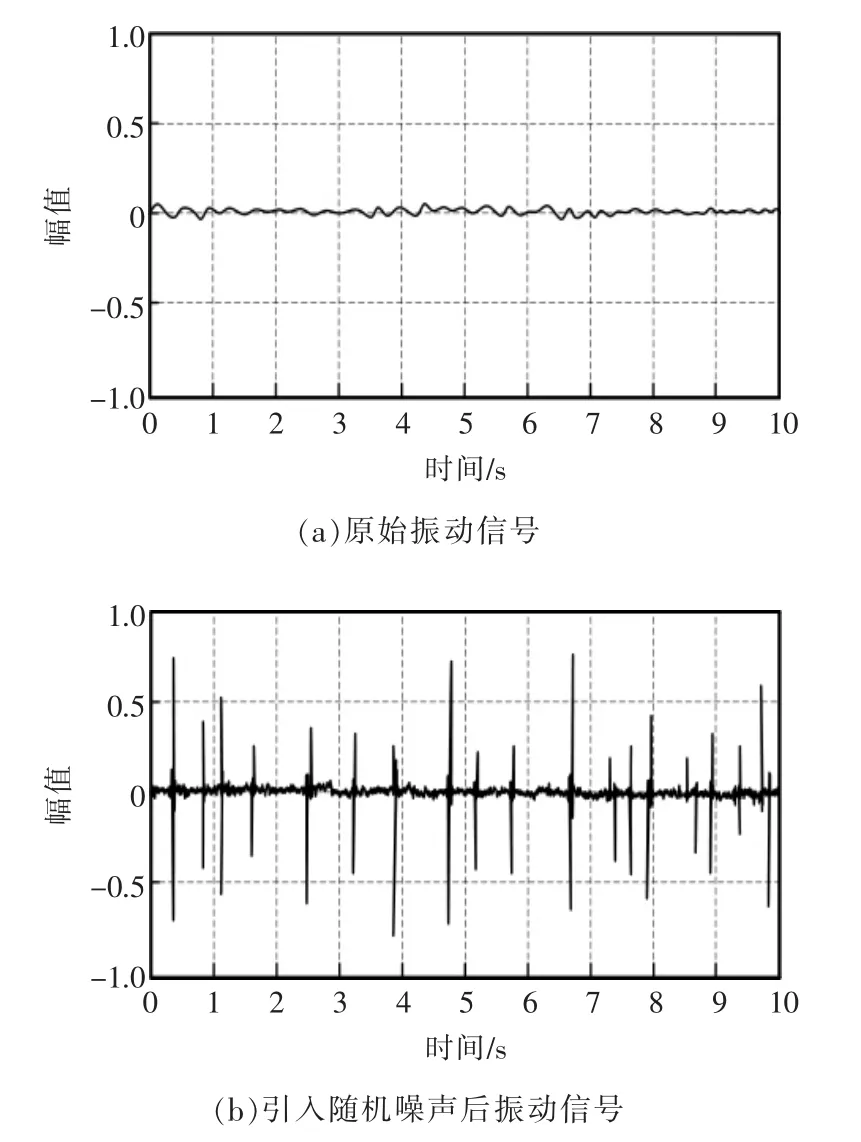
图1 大型水轮发电机组机械振动信号Fig.1 Mechanical vibration signal of large water turbine generator set

对比图1（a）和图1（b）可得出，受随机噪声影响，机组机械原始振动信号的波形已被噪声覆盖，且幅值也发生不同程度变化，这严重影响机组机械振动信号特征提取结果，不能分析出机组工作状态。

2.2 实验结果分析

2.2.1 振动信号噪声控制过程

为了进一步验证本文方法的有效性，以上述实验环境为基础，采用所提方法对含有随机噪声的振动信号进行处理，其处理效果如图2 所示。

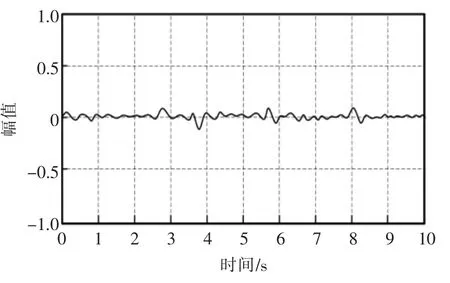
图2 经过所提方法处理后振动信号Fig.2 Vibration signal after processing by the proposed method

图2 中，经过所提方法噪声控制后机组机械振动信号与原始振动信号基本一致，仅有几个幅值不一致，但均在误差范围内。因此可以得出，所提方法的机组机械振动信号随机噪声控制效果良好。

2.2.2 振动信号噪声控制效果分析

信噪比、均方根误差是评价机组机械振动信号随机噪声控制性能的关键指标。

信噪比值越小表明此方法噪声控制能力越差，反之越好，通常用SNR 表示，计算过程为

式中：n1描述采集振动信号数据点个数；y1*与yi分别描述机组机械第i 个振动点的噪声控制后与实际的信号。

均方根误差值越小代表此方法随机噪声控制越好，与SNR 值相反，计算过程为

为了进一步验证所提方法机组机械振动信号随机噪声控制精度，实验环境不变，分别选用奇异值分解、傅里叶与能量熵增量方法进行噪声控制，根据式（13）和式（14）求出这4 种方法的SNR 值、RMSE 值，结果如图3 所示。

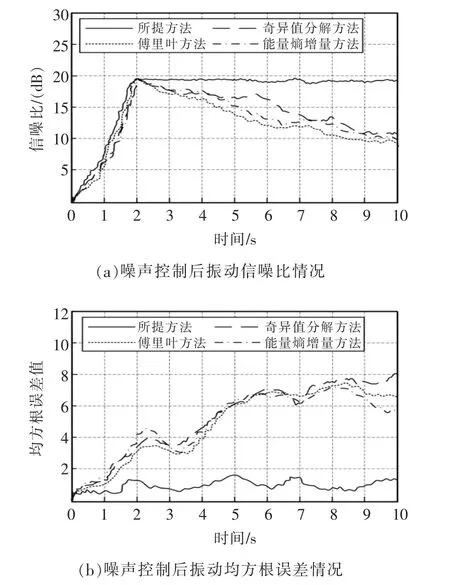
图3 各方法振动信号随机噪声控制对比Fig.3 Comparison of random noise control of vibration signals by different methods

分析图3（a）可知，4 种噪声控制方法在0～2 s内得出的信噪比相同。随着时间的增加，对比方法的信噪比曲线呈下降趋势，而所提出的方法的信噪比曲线基本不变，表明其随机噪声控制性能更为稳定，从而得到更高的信噪比；分析图3（b）可知，所提方法的均方根误差曲线始终在于对比方法之下，这是因为所提方法使用Stein 无偏似然估计确定小波系数阈值，RMSE 值较小，均在2 以内，从而提升噪声控制精度。

2.2.3 控制运行时间分析

计算运行时间也是检测机组机械振动信号随机噪声控制性能重要指标。实验设有4000 个采样点数，选用奇异值分解、傅里叶与能量熵增量与所提方法进行随机噪声控制，对比分析运算时间，如表1 所示。

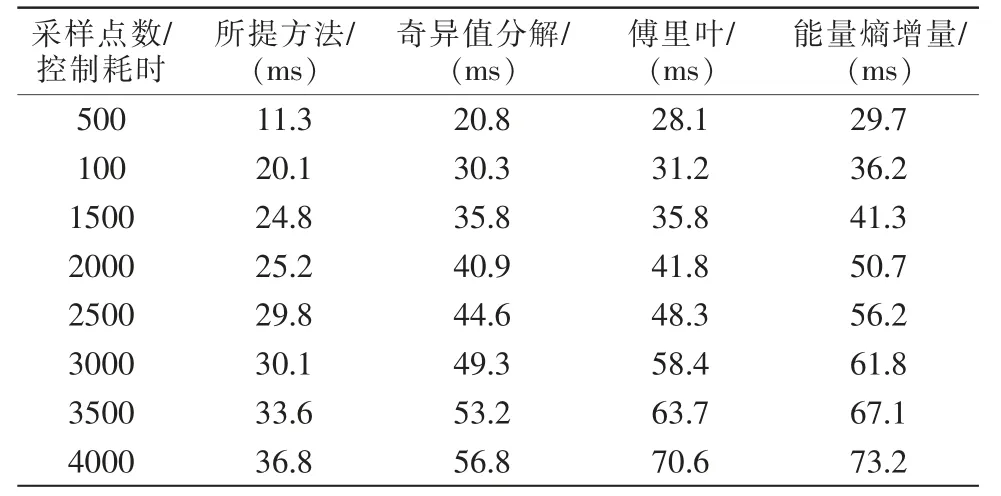
表1 振动信号随机噪声控制算法运行时间分析Tab.1 Analysis of running time of random noise control algorithm of vibration signal

根据表1 可知，所提方法随机噪声控制运算时间最短，由于所提方法采用能量差方式方法确定振动信号分层最佳参数，在保证随机噪声控制精度前提下，节省大量运算环节，为此36.8 ms 即可完成4000 个采样点振动信号随机噪声控制，而奇异值分解、傅里叶与能量熵增量至少需要56.8 ms 才能完成噪声控制任务。

3 结语

为了解决大型水轮机机组机械振动信号受外界干扰的问题，提出了一种随机噪声控制方法。该方法采用变分模态分解法和拉格朗日函数对含有随机噪声振动信号进行模态分解，并利用能量差算法确定模态分解层数。然后，使用小波阈值降噪方式控制各模态随机噪声部分，将剩余信号进行重构，得出机组机械实际振动信号。实验结果表明，该方法能够有效地控制机组机械振动信号中的随机噪声，且控制后信号的信噪比较高，均方根误差较小。