基于单锚点UWB的室内定位技术

石豪东，付 铭，夏雨啸，刘银华

（青岛大学 自动化学院，青岛 266071）

随着经济发展不断地提高，民生科技的需求增加，大量服务于人们生活的机器人随之出现，例如扫地机器人、预警机器人等。

这些产品的出现意味着人们对定位技术精度和可靠性的要求不断提高，各种新型定位技术和算法也应运而生。市场上的室内定位技术层出不穷，WiFi、红外定位、蓝牙等技术已经大量应用于室内定位，但对于复杂环境下尤其是非视距环境（none line of sight，NLOS）下，WiFi 和红外定位技术会因信号的衰减或者是障碍物的遮挡而导致定位产生很大的误差。在环境复杂的室内场所GPS、北斗等卫星定位技术由于卫星信号较弱，无法穿透屋顶、隧道等障碍，这导致此类定位技术无法用于室内环境[1]。而基于UWB 的定位跟踪技术具有定位精度高、鲁棒性好、适应性强等优势，已经成为当前定位技术中的研究热点。

UWB 定位系统是基于超宽带通信的，超宽带通信因为其高频特性，能够较容易地获取时间信息，基于时间特征的定位技术能够获取到更高精度的定位结果[2]。在文献[3]中描述了一个精度可以达到4 cm 的超宽带定位系统与之比较的是GPS 定位系统，实验结果表明超宽带技术的效果非常优越。UWB虽然可以实现高精度的定位，但是需要多锚点的距离信息共同计算目标位置，如果减少UWB 的锚点数量，就会导致位置信息的丢失，无法准确定位。

惯性传感单元（inertial measurement units，IMU）集成了加速度计、角速度计和磁力计3 种传感器，得益于其成本较低、体积较小以及精度较高，其在姿态识别、导航定位等研究领域中被广泛使用。但由于其具有零偏以及随意游走的误差特性，所以单独使用IMU 时误差较大。

UWB 无线信号虽然可以提供高精度的距离测量数据，但由于受到障碍物和信号衰减的影响，它在室内或者复杂环境下的定位精度受到限制。而IMU 惯性传感器可以提供相对运动状态的信息[4]，但随着时间的推移，它的误差会不断累积，从而导致定位精度下降。为了克服UWB 和IMU 各自的限制，研究者们提出了许多融合算法和滤波算法[5]，卡尔曼滤波算法是一种常用的滤波算法，它可以通过处理UWB 和IMU 数据，得到更加准确和可靠的目标定位跟踪结果，但在非线性系统中卡尔曼滤波技术的稳定性和鲁棒性有待提高，考虑通过扩展卡尔曼滤波（EKF）将UWB 和IMU 所提供的位置信息进行融合，通过融合这两种数据来提高定位精度和鲁棒性。

因此，本文旨在探讨基于UWB 和IMU 的定位技术，并利用EKF 算法进行数据处理，以提高定位精度和鲁棒性。在系统设计和实验过程中，将对UWB和IMU 数据进行预处理，构建数学模型来描述目标运动状态，利用EKF 算法进行数据融合和滤波处理，以实现高精度和鲁棒性的目标定位跟踪。

1 定位系统架构

1.1 UWB 系统

UWB 通过窄脉冲实现高带宽信号传输，传输速率高，不容易被其他信号影响，从而能实现高精度的目标定位。其测距原理为检测多个锚点之间的信号传输时间（TOF）和信号到达时间（TOA）计算两个节点之间的信号的接收与发送的时间，记录响应时间差通过式（1）即可获得信号的平均飞行时间ttof：

根据式（2），即可完成测距，其中c 为光速：

如图1 所示，计算出2 个节点之间的距离后，根据文献[6]中的描述，超宽带定位系统在预设位置上部署固定节点的情况下，可以通过最小二乘法的三边定位法，如图2 所示，计算锚点与固定节点的距离从而获得目标的位置信息。

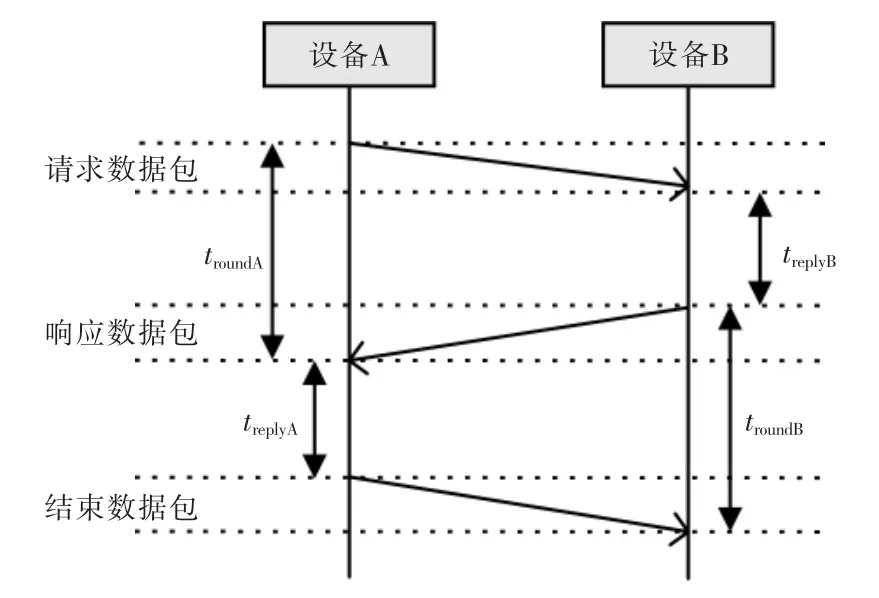
图1 UWB 测距原理图Fig.1 UWB ranging schematic diagram

图2 三边定位原理图Fig.2 Three-sided positioning schematic diagram

1.2 惯性导航系统

IMU 定位系统需要设置载体坐标系与导航坐标系，所述的载体坐标系（b 系）Y 轴指向前进方向，X 轴水平向右，Z 轴垂直向下；导航坐标系（n 系）采用北东地坐标系；姿态角由载体坐标系到导航坐标系之间的相对角位置关系来表示，用欧拉角来对目标姿态进行描述，欧拉角包括俯仰角、横滚角和偏航角，俯仰角是坐标系沿Y 轴旋转的角度，旋转范围为-90°～+90°；横滚角是坐标系绕X 轴旋转的角度，旋转范围为-180°～+180°，偏航角是坐标系绕Z轴旋转的角度，旋转范围为0°～360°。

两个坐标系之间的相互转换可以用姿态矩阵来表示：

上述矩阵可记为

则通过上述2 个矩阵的关系可以获得3 个姿态角（横滚角、俯仰角、偏航角）的计算公式分别为

1.3 单锚点的UWB 设计

配置多个锚点的UWB 定位技术难点在于定位目标时，目标机器人为节点，所构架的多个锚点如果与节点时钟不同步就无法使用上述的三边定位法计算目标位置。而且需要在预设的场地提前安装校准锚点，需要大量的前期人工工作。如图3 所示，现实生活中多是随机化的场景，所以提前构建场地安装锚点是很难实现的。

图3 UWB 锚点设置Fig.3 UWB anchor setting diagram

单锚点技术实现目标定位，不再需要繁杂的设备安装，而且有效地降低了技术成本。本方案虽然简化了系统构建的复杂度但还存在一个问题，如果只保留一个UWB 锚点，即只通过单一信号源获得的距离信息完成精确的目标定位是远远不够的。所以在只有一个UWB 锚点的情况下，需要加入其他传感器来获得目标的位置信息，采用从低成本的IMU传感器中观测目标在3 个轴向上的加速度和角速度，从而获得目标的姿态信息，结合UWB 提供的位置信息经过扩展卡尔曼滤波算法进行数据融合从而获得精确的位置估计。

2 系统数学模型

在本节中阐述了如何实现两种传感器数据的信息融合，以及模型的构建。基于数学运动模型进行多传感器融合，根据现实生活中机器人的运动状态通常是在匀速状态下进行的，所以采用二阶的CTRV模型作为系统的状态模型。该模型的运动状态为位置、速度、加速度和方向。CTRV 模型假设对象以恒定的角速度进行匀速运动，加速度为系统的过程噪声，通过加速度噪声对系统进行误差补偿，减少震荡，提高系统的精度与稳定性，增强系统的鲁棒性，其中估计器一般使用卡尔曼估计器计算出目标位置，如式（8）和式（9）所示：

式中：xk为状态向量，描述了机器人在坐标系中的位置和速度信息；uk为输入向量机器人的加速度和角速度信息；zk为观测向量，包含了机器人的位置和方向信息；fk为状态转移矩阵；Bk为控制输入矩阵；hx为观察矩阵；其中wk（0～Q）和vk分别表示过程噪声和传感器噪声描述了状态转移过程中的不确定性，它们都是符合高斯分布的白噪声。

由于机器人的运动过程并不是一个连续的线性的过程，无法用传统的卡尔曼滤波器进行位置信息估计。

对于非线性系统可以将机器人的运动和对其测量过程作为一个扩展卡尔曼滤波问题来进行建模，对系统函数进行泰勒级数展开从而把系统线性化，然后再使用卡尔曼估计器获取系统位置信息。基于传统的卡尔曼滤波系统线性化获得的扩展卡尔曼滤波，如式（10）和式（11）所示：

扩展卡尔曼滤波分为预测和更新2 个阶段，如图4 所示。预测阶段的控制输入由IMU 中的陀螺仪、加速度计和磁力计提供，在更新阶段使用的观测信息是UWB 模块测量的距离信息和IMU 测量的偏航角。

图4 系统估计框架Fig.4 System estimation framework

2.1 位置信息的估计

本文需要构建CTRV 模型来描述目标的运动状态。CTRV 模型是一种广泛应用于目标定位领域的模型，可以描述目标在三维空间中的位置、速度和加速度等状态。在本系统中，以二维平面展开描述，且其运动状态服从恒定加速度模型。

机器人的状态向量X=[PxPyvθ]T，其中x 和y 分别表示机器人的横纵坐标；v 为线速度；θ 为偏航角为角速度。

式中：Px，Py分别为机器人在x 和y 方向的位置信息，系统状态方程描述了目标在时间t 时刻的状态，包括位置、速度和加速度，由于加速目标匀速运动所以加速度a 为0，θ¨角加速度为0，即状态方程XK+1可表示为

式中：Δt 为采样时间；θt为t 时刻的角度。在本系统中，将UWB 和IMU 数据进行融合，以提高定位精度和鲁棒性。因此，系统的状态方程是由IMU 传感器数据和系统状态向量组成的，即在EKF 的预测阶段通过状态转移矩阵fx来描述目标的运动状态演化过程。使用IMU 模块通过陀螺仪、加速度计、磁力计计算物体的加速度和角速度，然后将其输入到预测模型。由于状态转移函数是非线性的，因此需要对其进行线性化。具体而言，在每个采样时间将状态向量作为一个局部线性近似点，并使用其一阶导数构建一个线性模型，这个模型通常被称为扩展卡尔曼滤波中的雅可比矩阵。状态转移函数的雅可比矩阵式可以通过求解矩阵的偏导数计算得到：

2.2 误差分析

本文把UWB 测量的距离和IMU 测量的角度θ作为观测向量Hx，系统的观测方程为hx，即：

UWB 模块通过式（17），测量物体与锚点之间的距离d 为

在EKF 的更新阶段，通过计算卡尔曼增益来融合IMU 和UWB 的观测值，得到一个最终的估计值。卡尔曼增益是一个重要的参数，用于确定如何将当前的观测信息与先前的估计值进行融合。所以卡尔曼增益的计算为系统估计的关键。

式中：Kk为系统的卡尔曼增益；Jh为观测矩阵的雅可比矩阵；Pk为更新误差的协方差矩阵；Pkˉ为先验误差的协方差矩阵；Q 为误差的协方差矩阵，可由式（21）计算获得：

将获得的测量值作为观测向量输入到扩展卡尔曼滤波器中，以获得更加准确的位置和速度估计值。

本系统的误差主要来自于加速度，虽然假设系统加速度a 和角加速度θ¨为常数，但在实际的运动中，速度的改变是无法忽略的，所以过程噪声会影响系统的准确性，需要在更新阶段对系统进行误差补偿可以更加符合真实轨迹，wk是一个零均值的高斯白噪声向量，即：

3 实验与分析

3.1 实验设计

为了验证该算法的可行性与准确性，在自主研发的室内机器人，如图5 所示，搭载了Decawave 公司生产的DWM1000 芯片和自主研发的9 轴IMU，传输频率为50 Hz/s。DWM1000 芯片负责接收机器人与锚点间的距离信息；9 轴IMU 负责提供加速度信息用于系统预测与更新，通过WiFi 将两个传感器测得的位置信息传输到PC 端。给机器人设置一段固定路径，其原点为UWB 锚点所在位置，获取位置信息验证跟踪路径的准确性。

图5 实验小车Fig.5 Experimental car

3.2 实验分析

分别设置2 种轨迹，分析该算法的可行性，记录实验数据如表1 所示。

表1 跟踪误差数据分析Tab.1 Tracking error data analysis

首先对直线运动进行误差分析，如图6 和图7所示，在卡尔曼滤波的情况下，系统的平均误差大约在0.21 m，其中波动最大处超过了0.30 m，而经过扩展卡尔曼滤波处理下的跟踪轨迹的平均误差只有0.13 m，而且没有大幅度的波动。

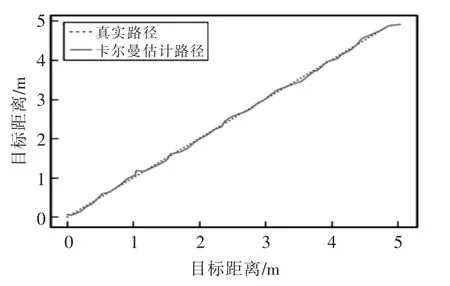
图6 卡尔曼滤波估计直线路径Fig.6 KF estimates linear paths

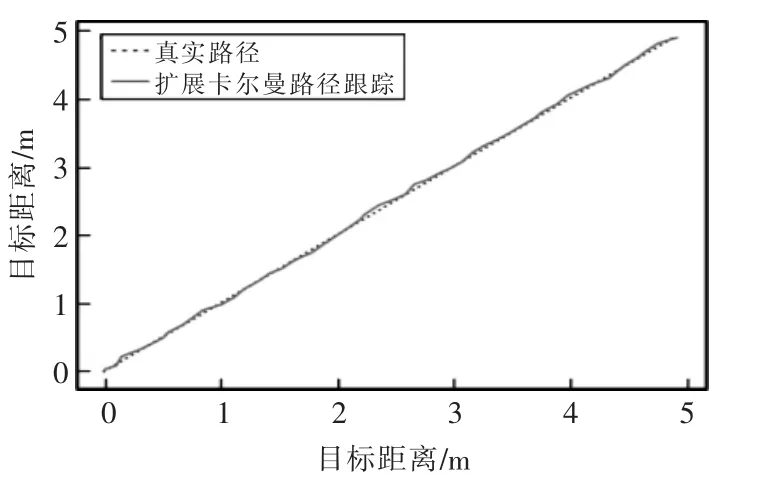
图7 扩展卡尔曼滤波估计直线路径Fig.7 EKF estimates linear paths

如图8 和图9 所示，在曲线轨迹下运动的小车明显出现了更大的误差，尤其是通过卡尔曼滤波器估计出的位置有很大的偏差，平均误差甚至超过了0.5 m，而通过扩展卡尔曼滤波器所估计出的位置平均误差只有0.18 m。虽然在速度有大幅度波动时系统产生了较大的误差，但是系统可以快速的恢复稳定，具有良好的鲁棒性。

图8 卡尔曼滤波估计曲线路径Fig.8 KF estimates curve path

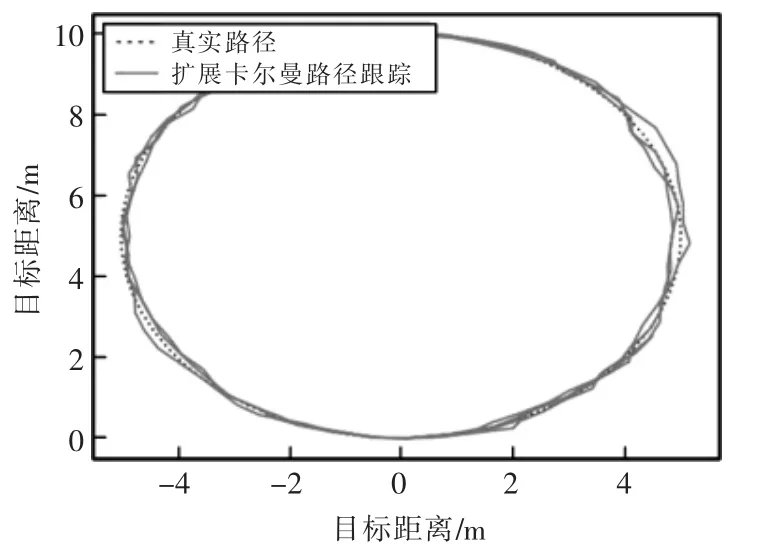
图9 扩展卡尔曼滤波估计曲线路径Fig.9 EKF estimates curve path

4 结语

本文设计了一种单锚点的UWB 目标定位算法，通过扩展卡尔曼滤波实现UWB 和IMU 的数据融合，提高定位系统的精度。经过实验，单锚点的UWB 在IMU 的配合下可以大幅提高定位的精确性，验证了本方法的可行性。实验也表明了在速度发生突变时，系统误差增大，跟踪轨迹发生了漂移，影响了系统的准确性，这也是此方法存在的不足，后续的研究重点考虑解决速度发生突变时系统产生的漂移所带来的误差影响，提高系统的鲁棒性。