堤坝渗漏及结构破坏条件下渗流传热特性的数值分析

蒋中明,杨江寅,黄湘宜,廖峻慧,肖喆臻

(1.长沙理工大学水利与环境工程学院,湖南 长沙 410114; 2.长沙理工大学洞庭湖水环境治理与生态修复湖南省重点实验室,湖南 长沙 410114)

渗透破坏既是威胁堤坝安全的主要问题,也是堤坝破坏的主要形式[1]。准确探测渗透破坏的产生及扩展,可为防汛抢险的决策提供强有力的科学依据。近年来,以温度为对象的堤坝渗漏隐患探测技术成为研究热点[2-4]。美国、德国等国家最早将温度作为天然示踪剂,通过捕捉温度变化来研究堤坝渗漏情况[5]。该方法于20世纪80年代引入国内,后被称为温度示踪渗漏监测技术[6]。早期温度示踪渗漏监测技术需在水工建筑物或其基础内埋设大量热敏温度计,由于埋设点有限,其对温度场的监测不够准确[7]。随后兴起的分布式光纤温度测量技术克服了前者的不足,但需在堤坝内埋设大量光纤,工作量依然巨大,且在已建工程中难以实现。目前,红外热成像法凭借其非接触、无污染、速度快、可连续扫描等优点,成为堤坝渗漏探测技术研究的重点发展方向[8]。

深入分析渗漏条件下堤坝内部温度场的变化规律,探明渗漏出口处温度的演变特性是红外热成像堤坝渗漏探测技术的基础。国内外研究人员针对渗漏条件下堤坝温度场变化规律等方面开展了大量的研究,并取得了丰硕的研究成果。理论分析方面,罗日洪等[9]建立了稳定渗流影响下堤坝渗漏热流耦合模型,分析了坝体中渗流场对温度场的影响;苏怀智等[8]认为当渗流存在时,水体迁移将迫使土体温度与水温相适应,从而引起温度场的局部不规则变化。室内试验方面,倪枫[10]通过物理模型试验研究了不同入渗水头、渗漏通道及入渗水温等条件下堤坝温度场与渗流场的变化规律;马佳佳等[11]开展了多种工况下土坝渗漏的红外热像探测试验;Song等[12]采用水热耦合分析对堤坝渗流状况进行监测,提出温度可成为判断堤坝前期渗流状况的有效工具。数值模拟方面,陈建生等[13]提出了利用虚拟热源法研究坝基裂隙岩体中存在的集中渗漏通道,通过温度场来判定钻孔周围是否存在渗漏,并定量计算出渗漏量等参数;Yousefi等[14]以Shamil大坝为对象,研究了坝体内渗流对压力及温度场的影响,表明温度比压力更能反映渗流状态;张启义等[15]通过对双层堤基异常渗漏险情下的温度场进行计算分析,在渗漏通道出口处观测到明显的低温区;Cheng等[16]基于渗流传热理论,采用数值模拟法对土石坝渗漏过程中的传热特性进行分析,提出孔隙内渗流稳定后,饱和区与非饱和区之间会形成温差,进而可通过温度判断坝体内浸润线位置。

堤坝渗漏是一个十分复杂的非稳态过程,尽管堤坝工程渗漏问题已从单一场的研究向多场耦合方向发展,但在数值模拟方面依旧存在考虑的环境条件和边界荷载不够全面等问题。为此,本文在现有研究基础上,采用数值模拟方法,考虑堤坝工程实际边界情况,研究堤坝渗漏乃至结构破坏过程中温度场的演变特性,以期探明堤坝渗漏及结构破坏与温度场演变的内在联系,为基于红外热成像的堤坝渗漏隐患探测技术提供一条有益的实现途径。

1 数值模拟理论

1.1 多孔介质渗流传热理论

多孔介质渗流传热过程中涉及复杂的耦合作用。渗流方面,堤内及地下水的流动符合达西定律。假设流体和固体不可压缩,流体运动方程可参考文献[17]。传热方面,堤坝渗流是一个十分缓慢的过程,可忽略土体与渗水之间的能量交换,基于局部热平衡理论的对流-扩散热传导能量平衡方程可参考文献[18]。

1.2 多孔介质热流固耦合理论

多孔介质中土体、水及温度之间相互影响。基于多孔介质线弹性假设,当产生非等温渗流时,土体本构方程表述为[19]

σij=2Gεij+λεkk+αPδij-3βTbKb(T-T0)δij

(1)

式中:σ为应力;ε为应变;i、j、k代表坐标轴方向;G为剪切模量;λ为拉梅常数;α为比奥系数;P为孔隙水压力;δ为Kronecher符号;βTb为多孔介质热膨胀系数;Kb为多孔介质体积模量;T为温度;T0为参考温度。

1.3 土体结构损伤分析理论

沈珠江[20]基于连续介质力学基本概念,提出了考虑黏土结构破坏损伤过程的损伤模型,后被广泛应用于工程界。该土体损伤模型通过定义损伤系数,对各项力学及流体计算参数进行折减,以反映土体的损伤程度。损伤系数和损伤过程中任意时刻土体参数的损伤值为[21]

ω=1-e-(aεv+bεs)

(2)

E=ωE0+(1-ω)Ed

(3)

K=ωK0+(1-ω)Kd

(4)

式中:ω为损伤系数;a、b为拟合参数;εv为单元体积应变;εs为单元剪切应变;E、K分别为损伤后的弹性模量和渗透系数;E0为单元初始时刻弹性模量;Ed为单元定义损伤弹性模量;K0为单元初始时刻渗透系数;Kd为单元定义损伤渗透系数。

利用内嵌FISH语言实现基于FLAC3D的土体损伤计算,具体步骤如下:

a.读取单元初始参数,并保存在单元额外变量中,作为后续损伤计算的基准。

b.读取各单元的体积应变及剪切应变,采用式(2)计算各个单元的损伤系数值,并保存于第二个单元额外变量中。

c.根据各个单元的损伤系数值,采用式(3)(4)分别计算损伤过程中各个单元的参数值,并保存于第三个单元额外变量中。

d.运用FISH的赋值功能,将第三个单元额外变量赋值给模型的对应参数,由此实现对单元参数的损伤。

e.通过FISH的循环调用功能,将上述步骤反复执行,以模拟计算过程中土体单元实时损伤的效果。

2 模型有效性验证

2.1 饱和多孔介质流体热对流计算

饱和多孔介质中,流体流动时会携带热量而发生强制对流传热,流体静止时会由于内部温度差异导致密度不均匀,进而发生自由对流传热。Zhao等[22]提出了一种求解稳态饱和多孔介质流体自由对流问题的渐进逼近方法,解决了采用传统有限元方法难以得到准确对流解的弊端。本文通过引入文献[22]中饱和多孔介质中流体的热对流计算,验证FLAC3D软件求解多孔介质中渗流传热问题的有效性及准确性。文献[22]计算模型及监测点布置如图1所示,模型高度为10km,宽度为10km,厚度为1m,共计网格节点169个,单元总数144个,监测点5个。

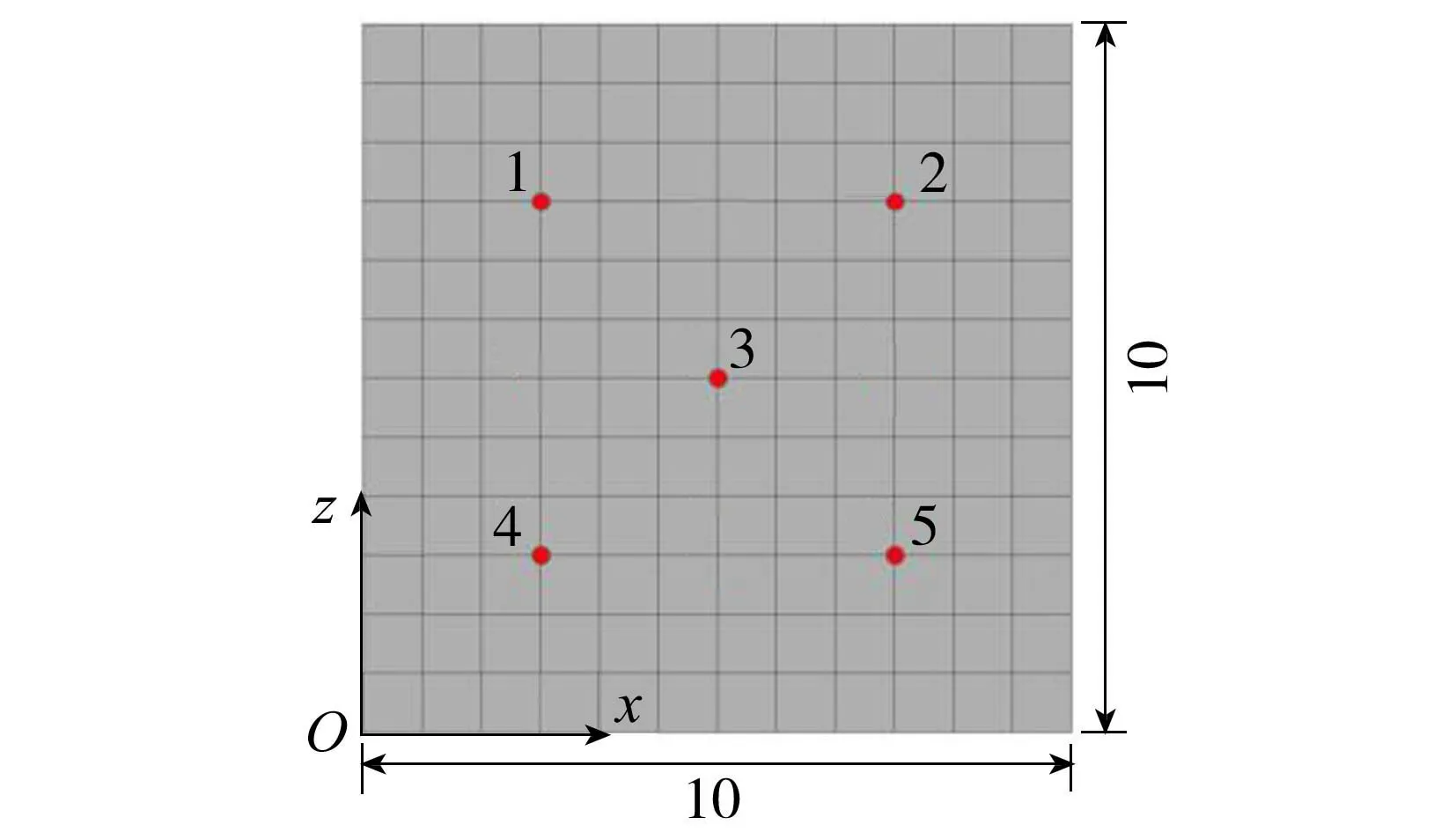
图1 热对流计算模型(单位:km)

渗流计算边界:左右两侧及上下两侧均为不透水边界。传热计算边界:顶面为固定温度边界,大小为20℃;底面也是固定温度边界,其值为220℃;左右两侧均为绝热边界。具体计算参数如下:渗透率为1×10-8m/s,孔隙率为0.1,导热率为0.335W/(m·K),比热容为803.2J/(kg·K),热膨胀系数为7×10-5K-1。图2为初始温度分布和初始孔隙压力分布图。

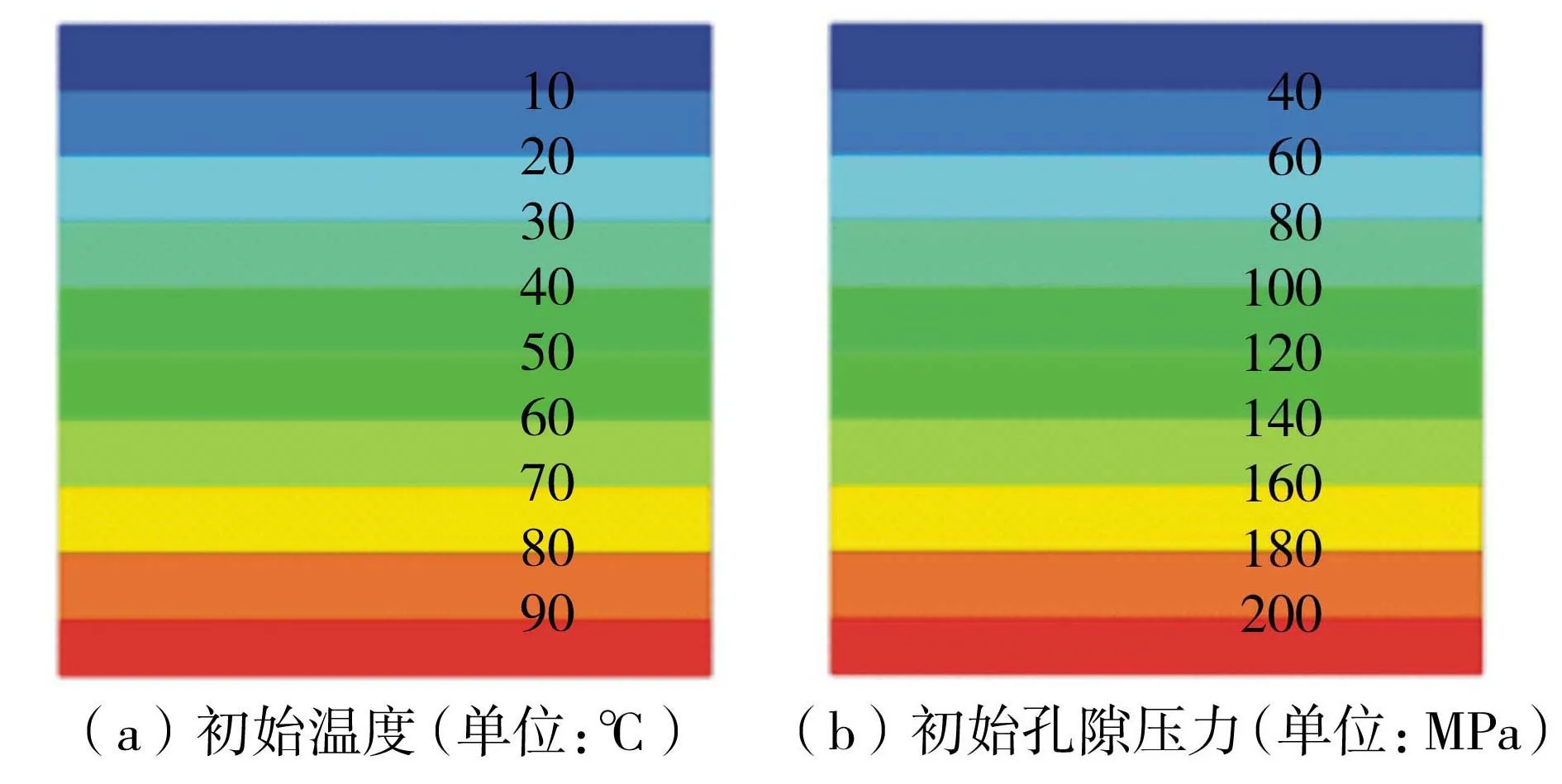
图2 初始温度和初始孔隙压力分布

给模型施加顺时针旋转的流速,驱动流体发生强制对流。随着强制对流现象的产生,多孔介质内的温度发生改变。当瑞利数大于临界值时,自由对流现象产生。最后,将初始设置的倾斜加速度去除,由流体内部温度差驱动流体发生自由对流。饱和多孔介质中流体自由对流的温度分布稳态解如图3所示(图3(b)为采用文献[22]的渐进逼近方法计算得到的解析解)。

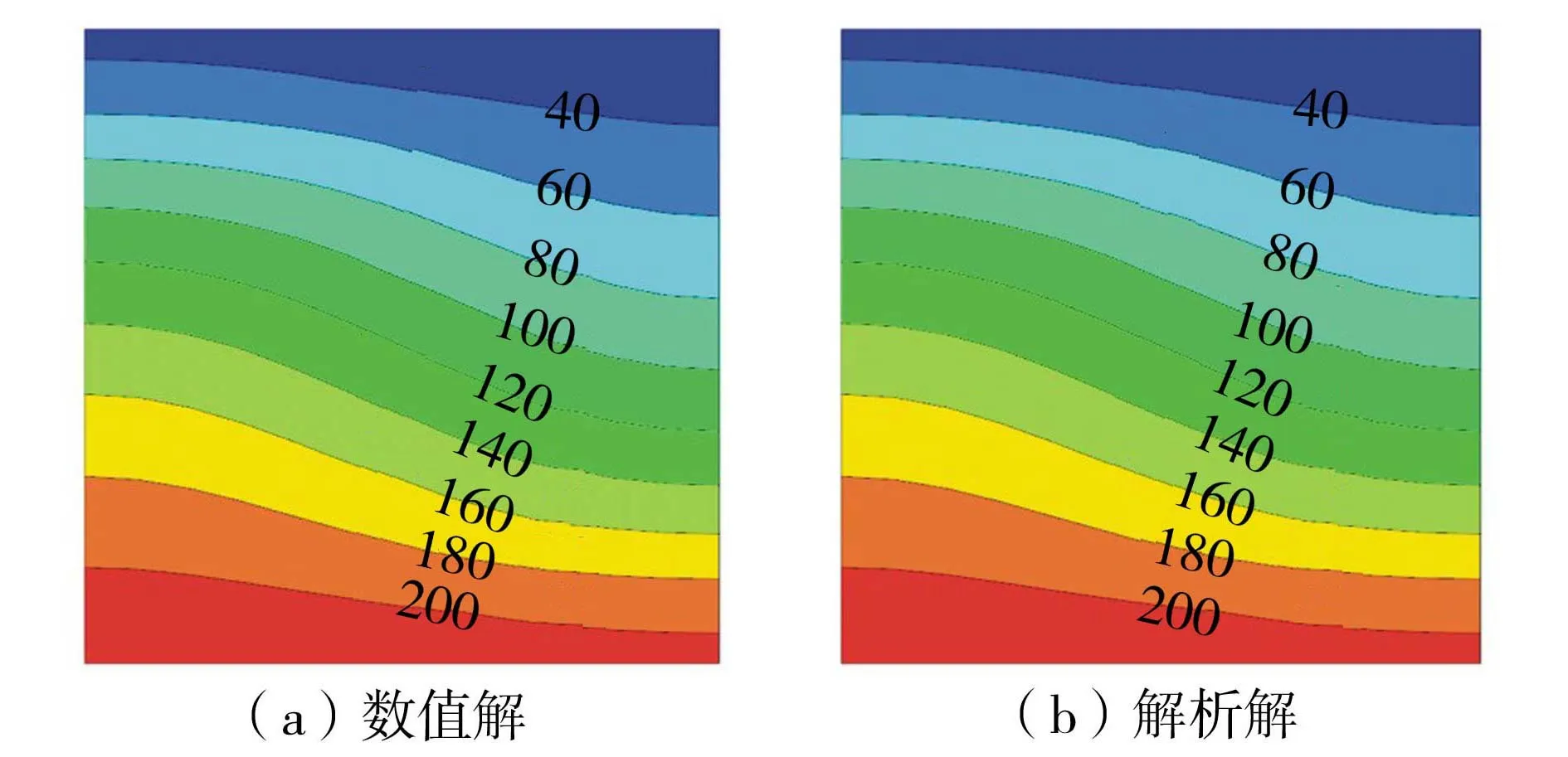
图3 稳态温度分布(单位:℃)

通过对比图2(a)及图3(a)可知,在自由对流过程中,流体携带热量运动,极大地改变了整体温度分布;对比图3(a)及图3(b)可知,基于FLAC3D软件计算得到的温度数值解与采用文献[22]方法计算得到的解析解几乎吻合。为进一步判断两者拟合度,提取监测点温度分布并进行比对,结果见表1。由表1可知,数值解与解析解最大温度差值出现在1号监测点,为3.4℃,误差仅为3.89%。因此,基于FLAC3D软件计算得到的数值解与解析解高度吻合,渗流传热计算的有效性及准确性得以验证。

表1 监测点稳态温度值

2.2 饱和土热固结计算

饱和土在热固结过程中受外部荷载、孔隙压力、温度荷载的同时作用,伴随着孔隙水的排出、温度的扩散,土体内部的有效应力变化较为复杂。白冰[23]基于饱和多孔介质热-水-力完全耦合的控制方程,通过有限傅立叶变换及其逆变换,推导了土柱内部温度、孔隙压力和位移演化过程的解析表达式,并对一维热弹性固结模型进行解析求解;孙致学等[24]利用该解析解进行了热流固耦合模型的数值验证。为验证基于FLAC3D软件求解热流固耦合问题的有效性及准确性,本文引入文献[24]中经典一维饱和土的热弹性固结算例进行分析。计算模型及监测点布置情况如图4所示,模型高度为7m,宽度为3m,厚度为1m,共计网格节点1240个,单元总数570个,监测点4个,分别设置在z坐标为0、3.5、5.0、7.0m处。

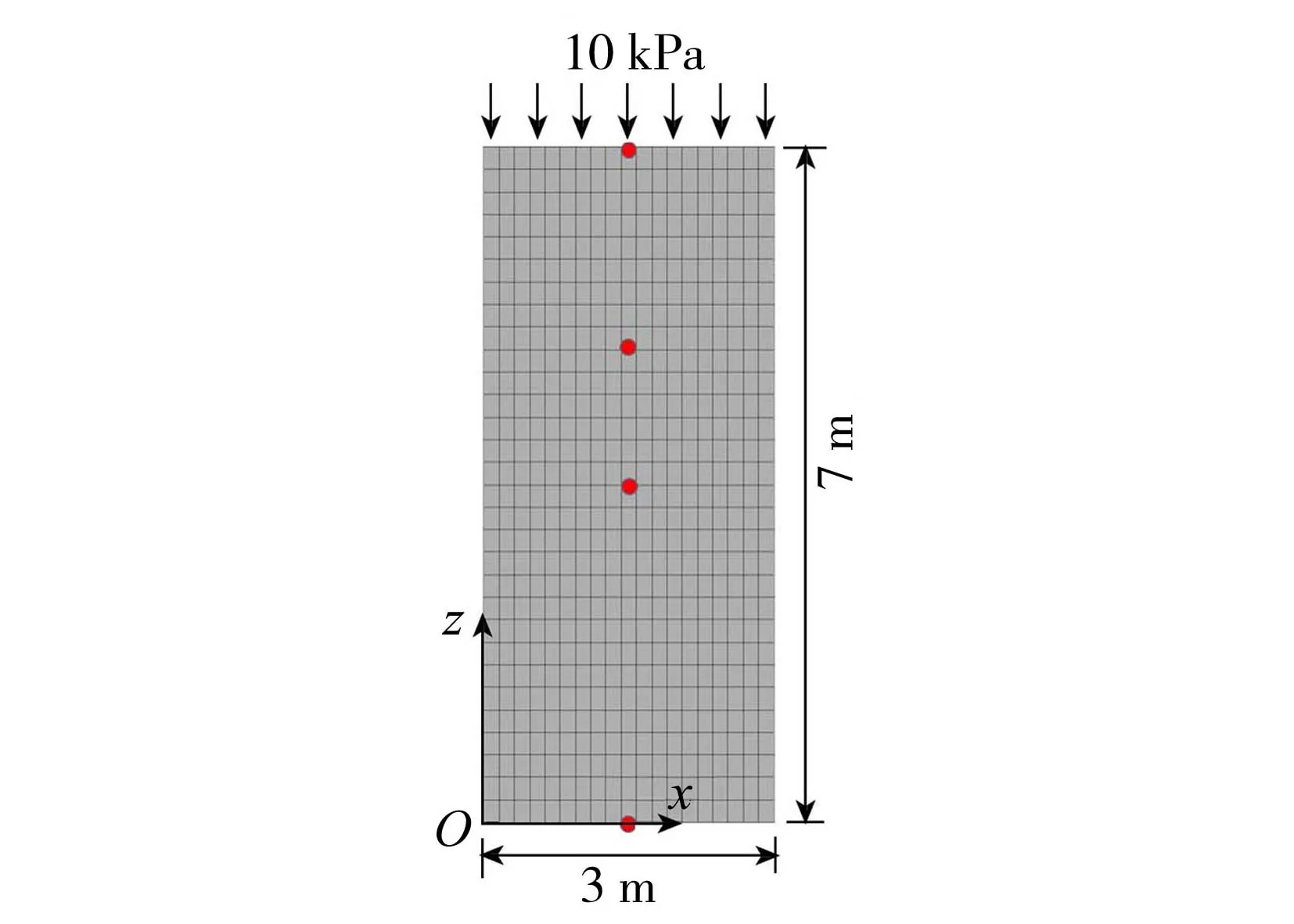
图4 热弹性固结计算模型

模型初始孔隙压力为10kPa,初始温度为10℃。力学计算边界:模型顶面受向下的均布荷载作用,大小为10kPa;模型左右两侧为法向位移约束;底面为固定约束。渗流计算边界:左右两侧及底面均为不透水边界;顶面为自由渗漏边界。传热计算边界:顶面受固定温度荷载作用,大小为60℃;左右两侧及底面均为绝热边界。具体计算参数如下:弹性模量为60MPa,泊松比为0.4,渗透率为4×10-6m/s,孔隙率为0.2,导热率为0.836W/(m·K),比热容为167.2J/(kg·K),热膨胀系数为3×10-7K-1,密度为2000kg/m3,流体密度为1000kg/m3。

图5为土体不同位置处竖向位移、孔隙压力及温度的解析解和数值解对比图,可见基于FLAC3D软件计算得到的数值解与文献[24]中的解析解高度吻合,其有效性及准确性得以验证。

3 模型应用与结果分析

3.1 工程背景

根据湖南省水利水电勘测设计研究总院2021年4月的《护城垸工程地质勘察报告》,护城垸位于洞庭湖区华容县,西南临藕池河东支,东靠华容河,垸内总面积364.6km2,总人口37.8万人,是洞庭湖区重点堤垸。该垸一线大堤分华容河段和藕池河段,总长82.816km,其堤防级别为Ⅱ级,建筑物级别为Ⅱ级。其中,华容河堤段桩号为70+030～76+790的断面堤身土质量较差,密实程度不均。1998年、2016年汛期该堤段堤身、堤脚出现散浸及渗水险情。

3.2 计算模型

以华容河堤段桩号为71+590的断面为研究对象,建立堤防计算网格模型。堤顶高程为35.97m,宽6.12m,堤身高6.47m,内坡比为1︰4,外坡比为1∶2.58。堤身为素填土,堤基由粉质黏土、淤泥粉质黏土及粉细砂层组成。计算模型堤身及堤基采用八节点六面体单元划分,共计网格节点数27882个,单元总数13640个。计算网格及分组情况如图6所示,计算参数见表2。

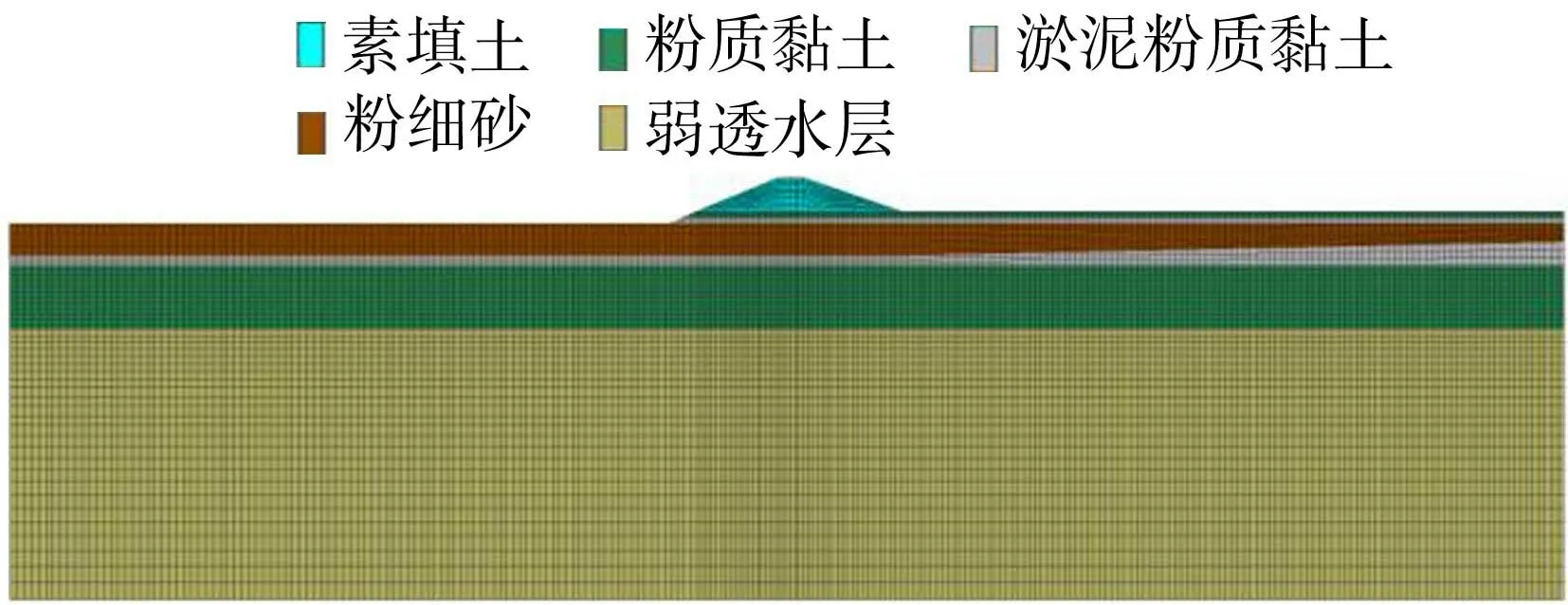
图6 计算网格及模型分组

为深入分析下游堤基及地表处渗透破坏及其传热特征,设置7个监测点用于监测各状态变量随时间变化的规律。测点1位于下游堤脚处,测点2、3、4位于下游堤脚附近地表处,测点5、6、7位于下游地表以下0.75m处的堤基表层,具体编号及位置如图7所示。

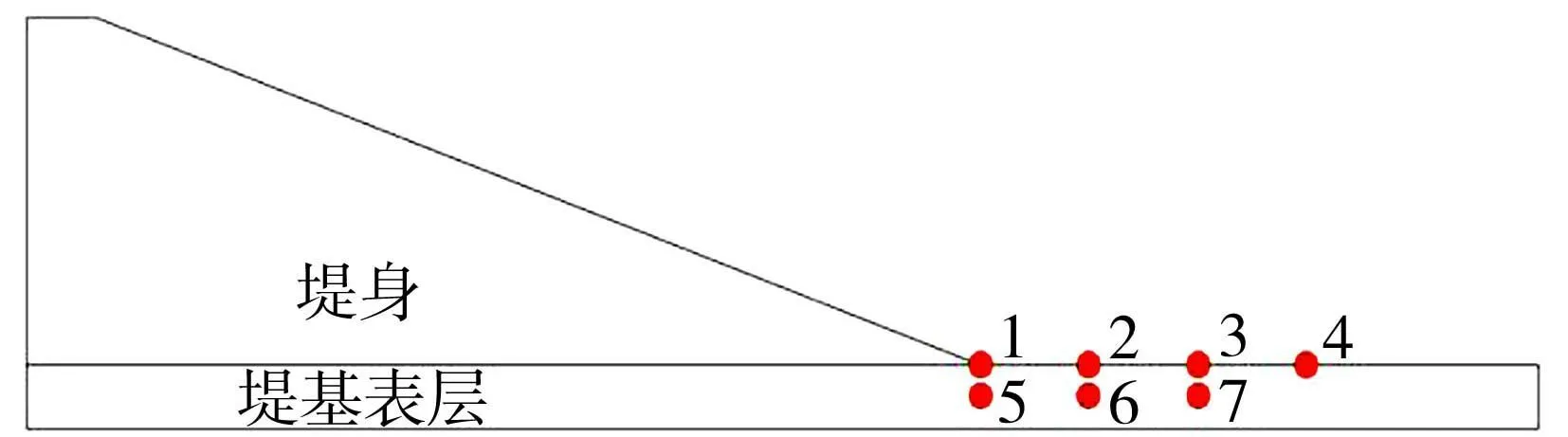
图7 模型监测点位置

3.3 计算方案及边界条件

洞庭湖水位受季节及气候的影响,水位高程变化复杂。为模拟堤防渗流实际情况,拟定计算工况为天然工况、初始工况及高水位工况。其中天然工况及初始工况为稳态计算工况,高水位工况为瞬态计算工况。

a.天然工况。为模拟堤防枯水期渗流及温度分布,拟定堤防天然工况为上游无水的情况。渗流方面,根据实测资料拟定地下水位。传热方面,模型底部温度为20℃,顶部由于受到气温的作用,拟定温度为25℃。

b.初始工况。渗流方面,拟定上游水位为2020年汛期华容河水文站平均水位,高程为30.8m。传热方面,拟定堤顶、堤防背水侧及下游地表温度为2020年夏季岳阳市平均气温,大小为28℃;拟定上游湖水表面温度为2020年汛期洞庭湖表层平均水温[25],大小为25℃;上游堤坡及堤基表面温度与水温一致,从上至下逐级递减,堤基表面温度为22.5℃;模型底部温度保持不变,大小为20℃。

c.高水位工况。据华容河水文站资料记载,华容河2020年汛期高水位持续时间长达40d以上。因此拟定计算时间为50d,以模拟长时高水位作用下堤防的异常渗漏情况。渗流方面,拟定堤防上游水位为华容河大堤保证水位,高程为35.5m。传热方面,拟定大气温度为30.6℃,堤顶及下游堤坡、地表处均为30.6℃的对流换热边界;上游堤基表面温度不变,为22.5℃;堤坡温度从下向上逐级递增,水面处温度为28℃。

3.4 计算结果分析

3.4.1渗流场分布特性

图8为不同工况孔隙压力分布图。天然工况下,在流体自重作用下,孔隙压力呈分层分布,从上至下孔隙压力逐级递增,水位线以下堤基土部位为饱和状态,以上为非饱和状态。孔隙压力最大值为0.12MPa,出现在堤基底部。初始工况下,在稳定水位的作用下,渗水进入了堤身及堤基内部,并与地下水连通。孔隙压力呈分层分布,且上游侧整体较下游侧大。在稳定高水位的作用下,堤内浸润线抬升,堤身非饱和区大幅减小,堤防整体孔隙压力左侧大于右侧,呈分层分布,孔隙压力最大值增加至0.14MPa,分布于上游侧堤基底部。

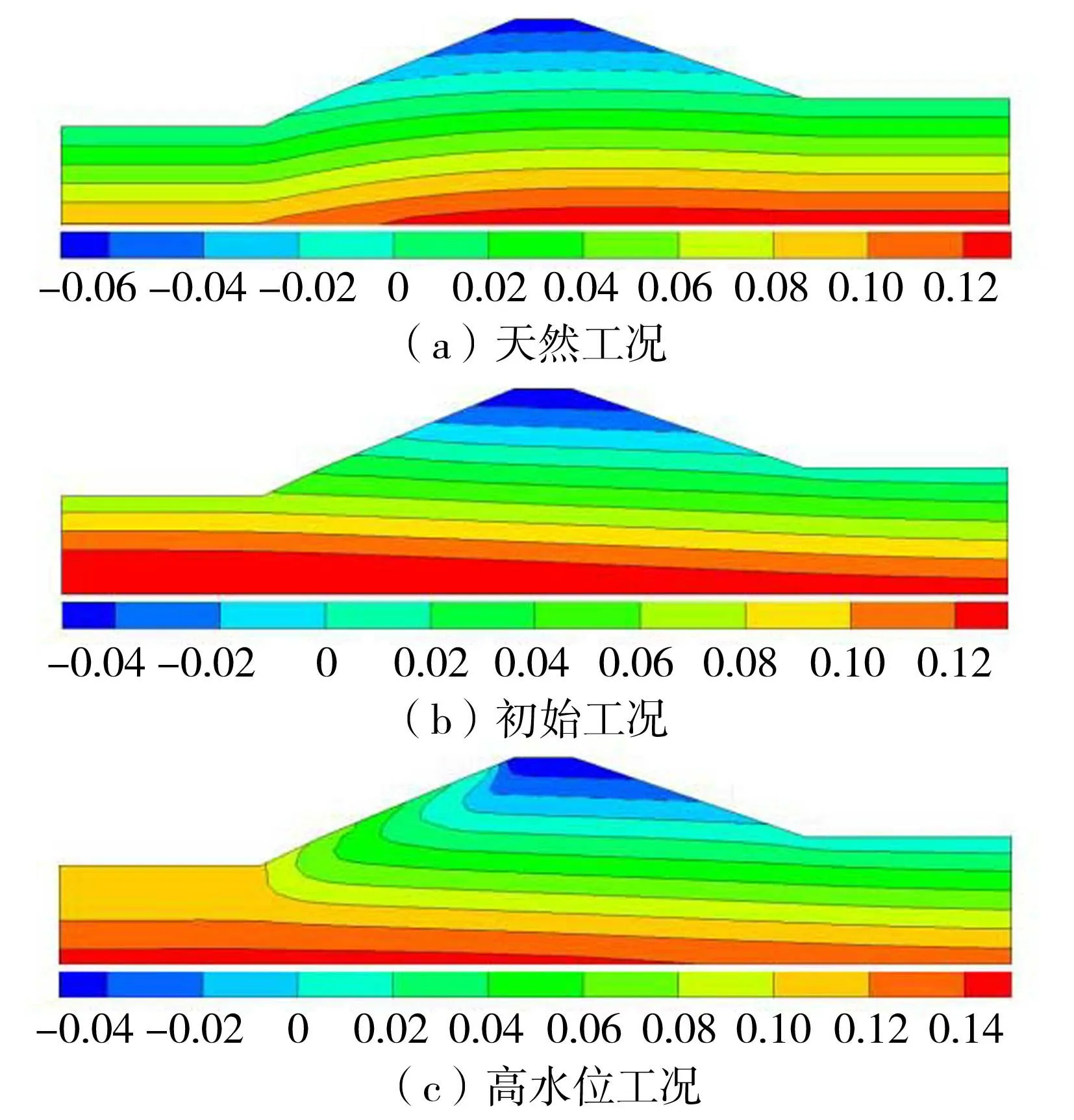
图8 不同工况孔隙压力分布(单位:MPa)

图9为高水位工况水力梯度分布图。堤防整体水力梯度左侧大于右侧,水力梯度最大值为2.4,分布于上游堤坡及堤脚处。此时下游堤脚处水力梯度为0.25。

3.4.2温度场分布特性

图10为不同工况温度分布图。天然工况下,在热传导作用下温度场呈分层分布,且由表及里逐级递减。温度最大值分布在堤防表面,大小为25℃;初始工况下,在夏季高温作用下,堤防表面持续升温,温度最大值达到28℃。在低温水体的强制对流作用下,温度最小值为22.5℃,分布于上游侧地基内部。由于水温低于堤基温度,导致上游处温度由表及里逐渐升高,堤内温度低于大气温度,导致下游处温度由表及里逐渐降低。高水位工况下,在强制对流作用下,下游堤脚处温度逐渐下降。在较高气温作用下,堤顶及下游堤坡处温度逐渐升高。随着渗流量的不断增加,下游堤脚处温度梯度逐渐增大,与周围地表及堤坡处温差较大。此时下游堤坡处温度为29.5℃,堤脚处为28.1℃。

3.4.3损伤场分布特性

图11为根据式(2)得到的高水位工况损伤系数及塑性区分布图。图11(a)表明,上游堤身大面积部位损伤系数值达到1.0,代表该处损伤情况较为严重。下游堤脚处损伤系数大小为0.14。图11(b)表明,塑性区与损伤系数分布位置与规律较为一致。上游侧堤身内部出现连贯的塑性区分布,此时堤身存在较大的安全隐患。

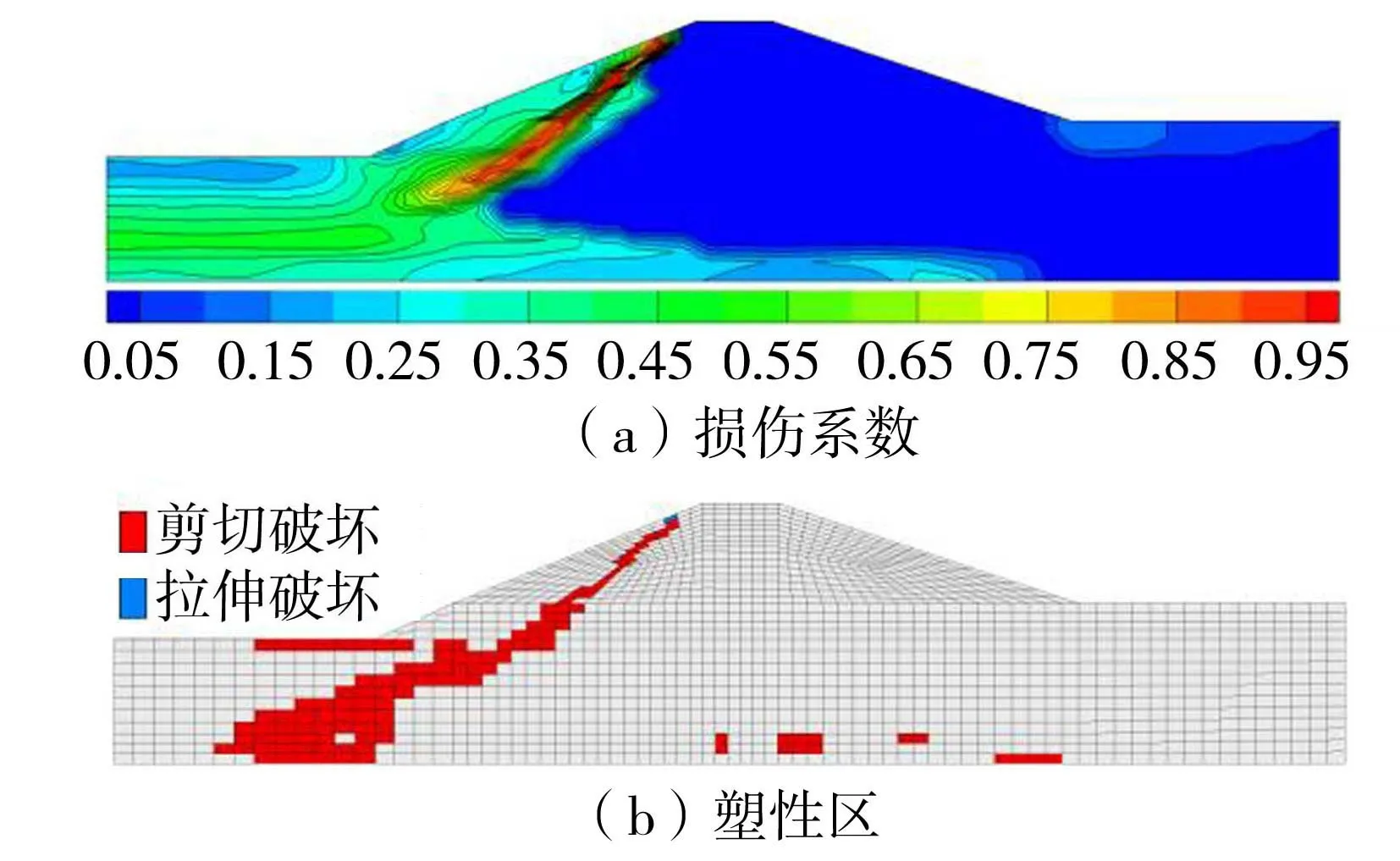
图11 高水位工况损伤系数和塑性区分布

3.4.4温度场与渗流场关联关系分析

由于不同位置处渗流场及温度场的分布形态均具有一定的差异性,难以把握渗流场与温度场的内在联系,需要针对性选取下游堤基及地表处测点,进行各状态变量的历时分析。

图12为堤防不同测点的孔隙压力、水力梯度及温度历时曲线。图12(a)表明,由于下游堤脚及附近地表直接暴露在大气中,渗水的及时排出使得孔隙压力得到释放,导致下游堤脚及附近地表处测点的孔隙压力曲线均低于堤基表层测点。随着时间的推移,下游堤脚及附近地表测点的孔隙压力随时间先急剧减小后缓慢减小,堤基表层测点的孔隙压力逐渐减小。

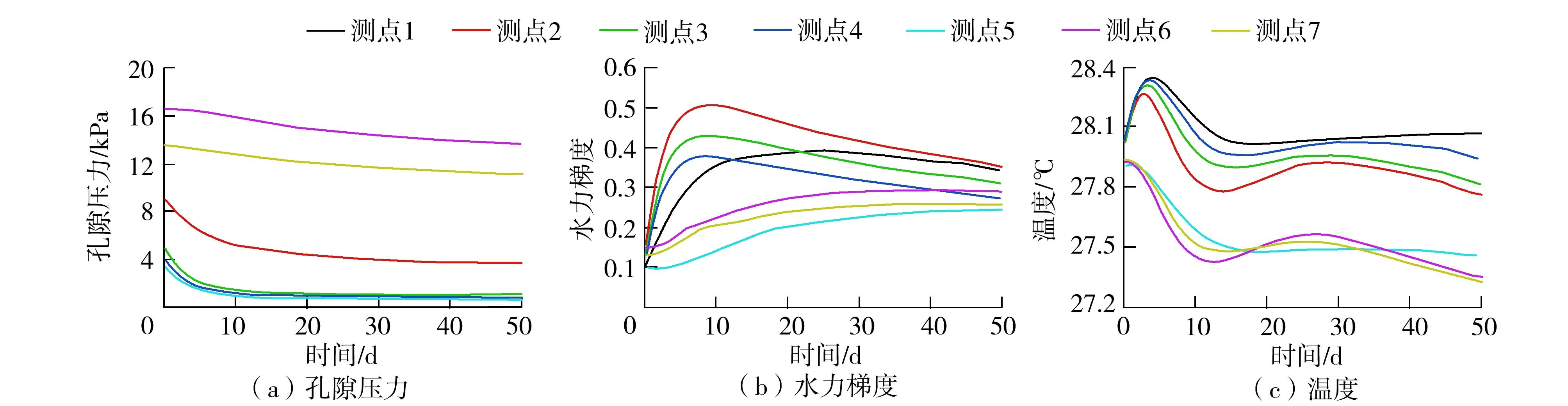
图12 各状态变量历时曲线

图12(b)表明,下游堤脚及附近地表处与大气接触,压力梯度较大,导致该处测点的水力梯度曲线均高于堤基表层测点。从整体上看,堤基表层测点的水力梯度随时间缓慢增大,下游堤脚及附近地表的水力梯度呈先急剧增大后缓慢减小的趋势。出现这种现象的原因是下游堤脚及附近地表处孔隙压力消散较快,较大的压力梯度使得水力梯度急剧增大;随着孔隙压力趋于稳定,下游堤脚及附近地表测点的水力梯度逐步减小。据《护城垸工程地质勘察报告》,堤基表层土体的临界水力梯度为0.32。随着水力梯度超过临界值,下游堤脚及附近地表处不同位置先后出现局部渗透破坏。首先是测点2,随之是测点3、4,最后是测点1。

图12(c)表明,在大气高温条件下,下游堤脚及附近地表处测点的温度曲线均高于堤基表层测点。堤基表层土体未直接与大气接触,受气温影响较小,因此温度的变化主要来源于内部水体的强制对流传热,且随着时间的推移,温度呈下降趋势。下游堤脚及附近地表土体受到渗水强制对流传热及大气高温的双重影响,该处温度变化趋势较为复杂。首先,由于短时间内下游堤脚及附近地表处还未产生较大流量的渗水,在大气高温条件下,该处温度升高;随着渗流现象的产生,渗水的强制对流传热效应显著,下游堤脚及附近地表处温度急剧降低;随着该处孔隙压力的消散,流速缓慢减小,强制对流传热效应逐渐衰弱。最终在渗水强制对流传热及大气高温的共同作用下,下游堤脚及附近地表处的温度趋于平衡。

对比图12(b)和图12(c)可知,随着堤基表层不同位置先后发生局部渗透破坏,各测点的温度值出现差异,差值约为0.18℃。因此可通过捕捉不同位置处的温度差来预测局部渗透破坏的发生。值得一提的是,此时温度差较小只能代表下游的局部渗透破坏,无法代表堤防整体渗透破坏或结构破坏的程度。

3.4.5温度场与堤防结构破坏表象关联关系分析

为进一步探明温度与堤防结构破坏表象的关联关系,采用FLAC3D软件内置的强度折减法进行堤防抗滑稳定性分析。图13为高水位工况下,通过强度折减计算得到的不同时刻的极限状态最大剪应变分布云图。由图13可知,随着时间的推移,最大剪应变数值不断增加。第40天前,堤防潜在滑裂面位于下游侧。随着上游堤身内部损伤面积不断扩大,第40天后堤防潜在滑裂面位置发生转移,上游堤坡发生滑坡风险较大。

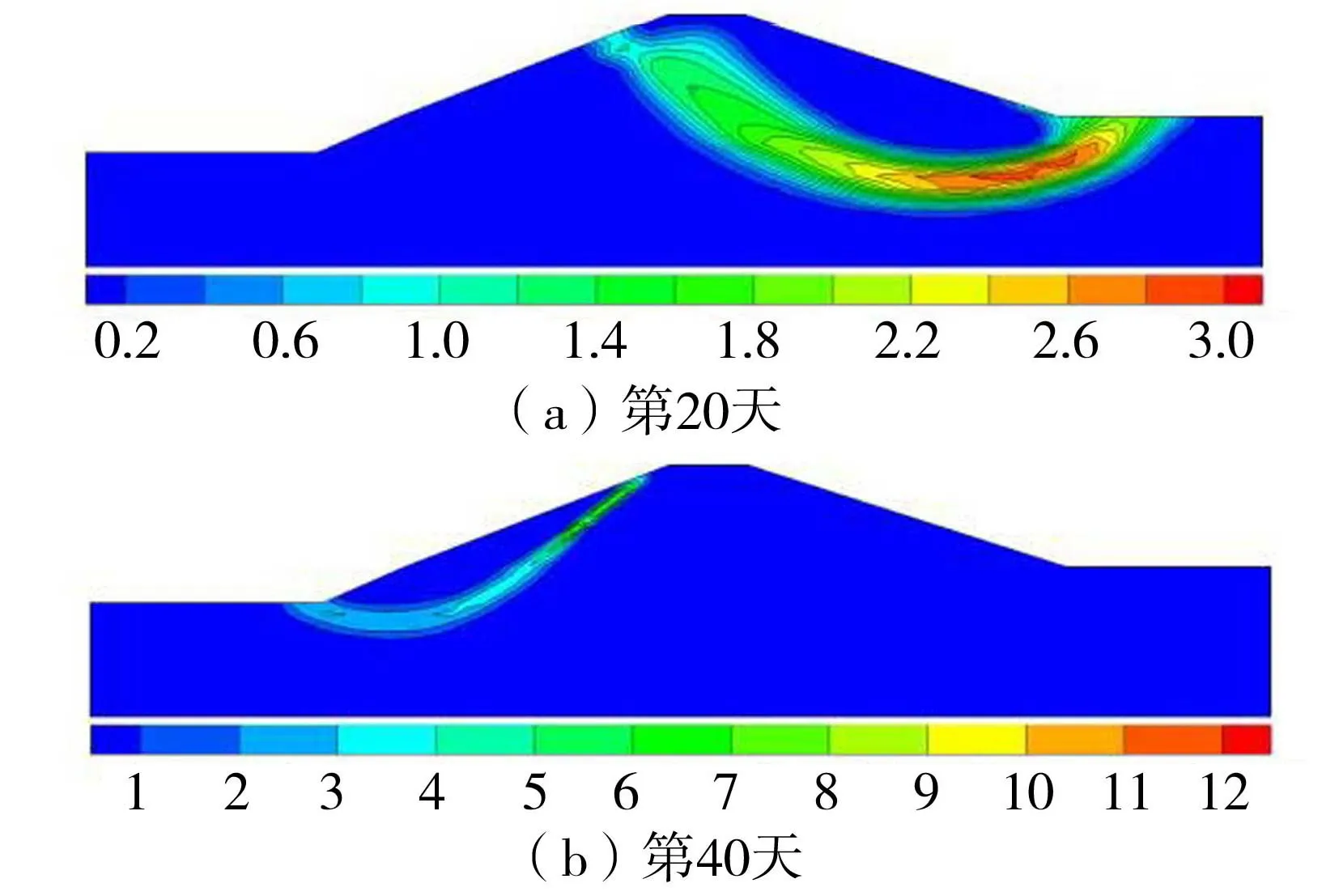
图13 极限状态最大剪应变

图14为堤防抗滑稳定安全系数历时曲线。在长时高水位作用下,堤身及堤基内部逐渐发生渗透破坏,堤防安全系数缓慢减小。从第40天开始,堤防安全系数急剧减小。根据GB 50286—2013《堤防工程设计规范》,Ⅱ级堤防正常运行条件下的安全系数允许值为1.35。由图14可知,前期堤防安全系数为1.53,处于稳定状态。第47天降低至允许值,此时发生大面积滑坡乃至溃堤的风险较大。通过对比可知,不同测点间温度差于第45天后突增,最大可达0.45℃,此时堤防整体安全系数急剧减小。

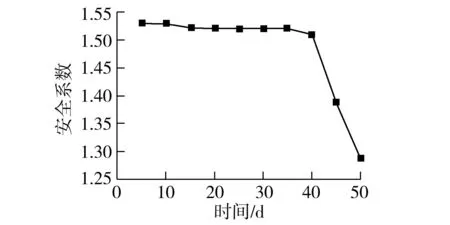
图14 安全系数历时曲线

综上所述,无论是下游堤脚处发生局部渗透破坏,或是上游堤身内部发生剪切破坏乃至滑坡,都会提前在下游堤脚及附近地表不同位置处出现明显的温度差值。随着渗透破坏的发展、上游堤身内部塑性区的延伸,下游堤脚及附近地表处的温度差值会逐渐增大。

4 结 论

a.堤坝渗漏过程中,下游堤基及地表处的温度演变有阶段性特征。首先,短时间内下游堤脚及附近地表处还未产生较大流量的渗水,在较高气温条件下,该处温度升高;随着渗漏现象的产生,渗水的强制对流传热效应显著,下游堤脚及附近地表处温度急剧降低;随着该处孔隙压力的消散,流速缓慢减小,强制对流传热效应逐渐衰弱;最终下游堤脚及附近地表处的温度趋于平衡。

b.随着下游堤脚及地表处水力梯度的不断增大,不同位置处先后发生局部渗透破坏,出现较小温度差,约0.18℃;随着时间的推移,堤身内部塑性区不断延伸,堤防安全稳定性逐渐下降。堤防安全稳定系数低于临界值前,下游地表不同位置的温度差进一步增大,达到0.45℃。

c.无论是下游堤脚处发生局部渗透破坏,或是上游堤身内部发生剪切破坏乃至滑坡,在下游堤脚及附近地表不同位置处均会提前出温度差值。随着渗透破坏的发展,该温度差值会逐渐增大。