简支条件下单轴对称三角形管翼缘工字形梁弯扭振动理论与有限元验证

张文福，江 杨，杨 琴

（1.安徽建筑大学 土木工程学院，安徽 合肥 230000；2.南京工程学院 建筑工程学院，江苏 南京 211167）

现在的建筑结构中梁截面主要形式是以工字形截面为主，工程中通常把它当作薄壁构件以减少重量、节约成本。然而工字形截面为开口截面，其扭转刚度较低，因此抗扭性能较差[1]。而对于闭口构件其抗扭刚度提升许多且不易失稳，为此国外学者提出了空翼缘工字形梁（THFB）的概念。文章将利用板-梁理论对上翼缘为三角形管的工字形梁进行弯扭振动的理论分析和研究。试图为该类新型钢梁的动力分析与工程设计提供参考。

近二十年来国内外学者主要集中在对空翼缘工字形梁屈曲以及梁抗弯承载力的研究，对扭转振动、弯扭振动研究较少。姜良芹等[2]从混凝土强度等级、钢管翼缘高宽比、腹板厚度等影响参数完成对14 根矩形钢管高强混凝土上翼缘工字形简支梁屈曲分析，明确其影响参数对屈曲荷载的影响规律。张文福等[3]基于板-梁理论对集中荷载作用下矩形钢管混凝土翼缘工字形梁弯扭屈曲分析，获得了弯扭屈曲下无量纲临界弯矩解析解。Senthilkumar R 等[4]通过改变空翼缘工字形梁的长度、宽厚比等影响参数研究了变形屈曲对空翼缘梁的影响。陈克珊[5]基于板-梁理论对单轴、双轴对称的钢管混凝土翼缘工字形梁进行弯扭屈曲分析，并给出了单轴对称钢管混凝土翼缘工字形梁截面不对称系数的计算方法。Kanthasamy E 等[6]对边缘加筋的圆形腹板开口双对称矩形空翼缘梁（RHFB）的抗剪能力影响进行了研究，并在强度法的基础上给出了抗剪能力的新设计公式。Raut K V 等[7]研究不同加劲方式作用下空翼缘梁的抗弯性能，研究了抗弯刚度、失效模式、挠度等参数，在实验与有限元结果显示下得出中间腹板加劲有较好的抗弯强度。魏建军[8]通过试验对三角形空翼缘梁（THFB）与传统的H 型钢的极限承载力进行研究。发现TFHB 比H 型钢具有更好的抗弯扭性能，并验证了H 型钢梁设计公式计算TFHB 极限承载力的适用性。Dissanayake D 等[9]利用Abaqus 有限元软件从截面高度、截面厚度等几何参数以及不同钢种的影响对矩形空翼缘梁、三角形翼缘梁剪切性能的研究，发现不锈钢空翼缘梁、三角形翼缘梁有较强的抗剪能力。Shao 等[10]对改善空翼缘工字形梁的局部屈曲状态提出一种加劲压缩矩形翼缘工字形梁，通过与常规SCHFB 和工字梁比较发现其极限承载力和外延性有显著提高。Masri等[11]理论分析了三角形翼缘工字形的梁的承载力计算公式。Mahen[12]对三角形翼缘工字形梁研究，发现使用横向腹板加劲肋可以有效消除横向扭转破坏。

在薄壁梁的振动理论和试验研究方面，近期的主要研究工作包括：张文福等[13]采用Timoshenko 梁的连续化模型来模拟三角形空间桁架梁振动分析，推导得到了桁架梁的等代抗弯刚度和等代抗剪刚度，并给出桁架梁的竖向振动频率和振型的解析解。韦忠瑄等[14]推导了波形钢腹板PC 组合箱梁弯曲振动频率计算公式，并与实验和有限元进行了对比，但对扭转振动特性方面的研究相对来说比较少。冀伟等[15]运用了D’Alembert原理，推导出了波形钢腹板PC 箱梁桥的扭转振动频率方程，并根据简支梁的边界条件求得了扭转振动频率的计算公式，并结合实验与有限元验证了该公式的可靠性。刘超星[16]基于能量变分法和Hamilton 原理，推导了波形钢腹板组合梁的扭转振动频率公式得到了扭转振动频率的理论解，并与ANSYS 有限元进行了对比，验证了该理论解的正确性。Xu 等[17]通过引入差分变换法（DTM）来分析弹性边界条件下旋转铁木辛柯梁的自由振动，结果表明：与传统的瑞利-里茨（R-R）法相比该方法具有更高的精度和计算效率。鲍四元等[18]在梁的两边施加横向约束弹簧和旋转约束弹簧通过改变弹簧刚度实现任意边界条件的转换，并采用改进的傅里叶级数和瑞利-里兹法求解获得了具有任意边界条件单跨梁结构的振动频率解。李伟等[19]采用微分变化法推导圆形变截面棒振动偏微分方程的级数解，并利用有限元软件分析对比，发现采用微分变换法对求解变截面梁振动的偏微分方程有较高的精度。曾在平等[20]研究了钢管混凝土翼缘工字形梁与等效截面工字形梁进行振动频率的对比，发现不同构造形式对钢管混凝土翼缘工字形梁振动特性的影响。

从目前查阅的文献资料可以看出，关于单轴对称三角形管翼缘工字形梁振动理论和试验研究方面的研究成果尚未见到。为了使单轴对称三角形管翼缘工字形梁在实际工程的方便计算和使用，利用“板-梁”理论求出单轴对称三角形管翼缘工字形梁弯扭变形总应变能和弯扭振动总动能，利用能量变分求解出简支条件下弯扭振动的频率解。建立相应的有限元模型并求解与板-梁理论解对比，验证“板-梁”理论的正确性。

1 研究对象

为了不失一般性，以图1 所示的单轴对称三角形管翼缘工字形钢梁为研究对象。钢梁的弯扭变形基于板-梁理论来分析。

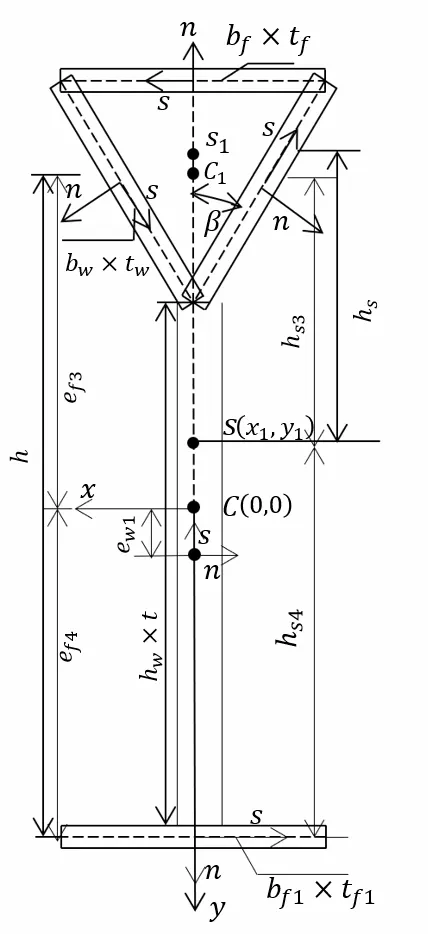
图1 截面尺寸图

已知：钢的弹性模量为E，剪切模量为G，泊松比为μ；三角形管翼缘中的上翼缘宽度为bf，厚度为tf；三角形管翼缘中的两块腹板宽度为bw，厚度为tw；工字形截面的腹板高度为hw，厚度为t；工字形截面下翼缘宽度为bf1，厚度为t。钢梁的长度为L，三角形管翼缘截面尺寸如图2 所示。当钢梁发生弯扭振动变形时，则未知量有横截面绕剪心的刚性转角θ（z）以及侧向位移u（z），截面弯扭变形图如图3 所示，其中三角形管翼缘部分不但会绕自身剪心扭转，还会受到刚性转角θ（z）影响产生偏移距离hsθ，三角形管翼缘截面扭转变形图如图4 所示。

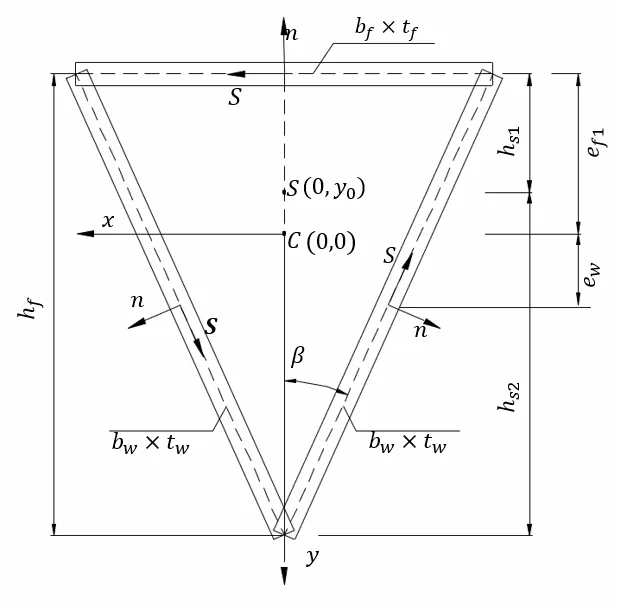
图2 三角形管翼缘截面尺寸图

图3 截面弯扭变形图

图4 三角形管翼缘截面扭转变形图

2 三角形管翼缘工字形梁弯扭变形应变能与弯扭振动动能

2.1 三角形管翼缘扭转应变能

根据应变能公式

2.1.1 三角形管翼缘截面上翼缘的应变能

其中，ψf为文中假定的待定函数。

2.1.2 三角形管翼缘截面左侧腹板应变能

其中，ψw1为文中假定的待定函数，b1为假定的待定系数。

2.1.3 三角形管翼缘截面右侧腹板应变能

其中，ψw2为文中假定的待定函数，b2为假定的待定系数。

2.2 截面转角与横截面的刚性转角之间的关系

（1）第一个关系为交点处纵向位移协调条件。

（2）第二个关系为剪力流相等。

两条件结合可以求得

其中，若令

则有

这便是截面刚性转角θ 与截面转角ψf、ψw1、ψw2之间的关系。

2.3 三角形管翼缘截面偏移应变能和弯扭应变能

（1）截面偏移应变能（受刚性转角θ 的影响产生偏移位移hsθ）

由公式（1）可得到三角形管翼缘截面偏移应变能

（2）截面弯扭应变能（侧向位移u 引起）

由公式（1）可得到三角形管翼缘截面弯扭应变能

2.4 工字形腹板、下翼缘弯扭应变能

（1）腹板弯扭应变能

（2）工字形下翼缘弯扭应变能

2.5 单轴对称三角形管翼缘工字形梁弯扭总应变能

单轴对称三角形管翼缘工字形梁弯扭变形总应变能为三角形管翼缘梁扭转总应变能、三角形管翼缘梁（刚性转角θ 产生的侧移）侧移应变能、三角形管翼缘梁（侧向位移u）弯扭应变能、工字形腹板与下翼缘弯扭应变能之和。

2.6 单轴对称三角形管翼缘工字形梁弯扭振动总动能

由动能公式

可知动能与n、s、z 方向变化的位移分量有关，分别将变化的位移分量代入公式（4）进行积分计算可得到单轴对称三角形管翼缘工字形截面弯扭总动能

其中

2.7 弯扭振动总势能、微分方程与理论解答

2.7.1 总势能

若令

将上述结果代入如下的欧拉方程，可得到单轴对称三角形管翼缘工字形梁振动微分方程

2.7.2 微分方程

使用微分算子法

令

可得

对于三角形管翼缘工字形简支梁除简支端外，由于其他位置u、θ 不为0，故行列式为0。

可解得第i 阶频率为

其中

3 理论解与有限元的验证

利用有限元软件ANSYS 模型，选用Beam189（该单元是基于铁摩辛柯梁理论建立的）单元进行模拟，Beam189 单元有三个节点，若打开KEYOPT（1）=1 开关，则每个节点有7 个自由度，分别为沿x、y、z 方向的位移自由度、绕x、y、z 方向的转动自由度以及横截面的翘曲，该单元适用于线性、大转动、大应变等问题分析。针对单轴对称三角形管翼缘工字形梁可能出现局部屈曲等问题，施加了刚周边命令进行模拟进而建立模型并求解，进入后处理可得到简支条件下各阶频率与振动模态。简支条件下弯扭振动第1 阶模态图如图5（a）所示，第2 阶模态图如图5（b）所示。

图5 简支条件下弯扭振动模态图

有限元数值模拟验证中，单轴对称三角形管翼缘工字形梁参数以及有限元计算的各阶频率与理论解答的对比结果见表1，其中弹性模量为2.06×1011Pa，泊松比为0.3。三角形上翼缘厚度均用t 代替。

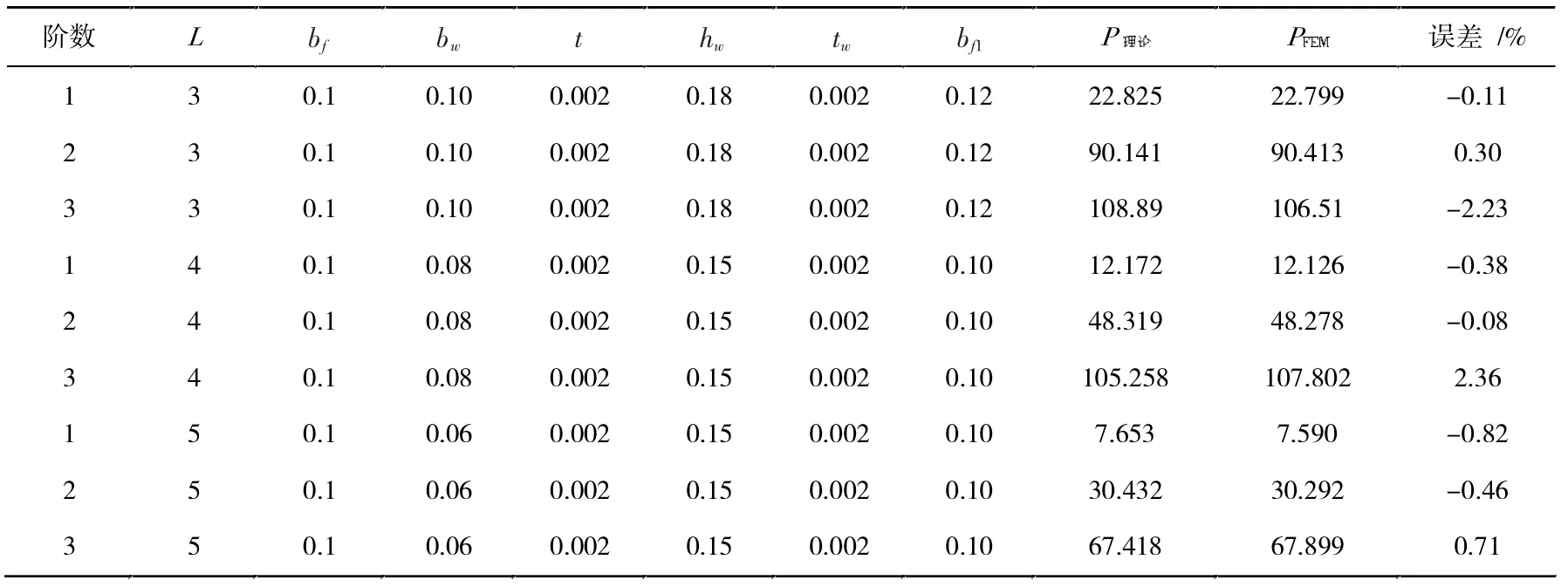
表1 单轴对称三角形管翼缘工字形梁的振动频率对比

4 结语

（1）基于板-梁理论推导弯扭振动总势能方程。依据能量变分模型和微分方程模型推导出简支梁弯扭振动公式。

（2）利用有限元软件ANSYS 建立相应的有限元模型及计算结果，对文中推导的弯扭振动进行验证。结果表明，弯扭振动公式的误差在-2.23%～2.36%之间，证明推导公式的正确性。